随着煤矿开采深度的逐渐增加,高应力环境下围岩岩性由脆性向塑性转化,使得深井巷道围岩常出现大变形状态[1]。当然,围岩承载能力的降低易导致支护结构失效,故锚喷联合以发挥围岩自承力并进行协同承载而得到应用,且喷浆层多以峰后承载状态与破碎围岩协同配合。因此,研究喷浆层损伤后的力学行为,将利于深井巷道围岩喷浆参数的合理选取。
深部巷道围岩存在“浅支撑层”和“深支撑层”[2],其围岩破坏方式特殊[3],覆岩破坏易形成“类双曲线”形态[4]。高水平应力、高主应力差、巷道埋深大、围岩松软破碎、巷道跨度效应及简单锚杆索支护未能与围岩耦合是巷道围岩支护失效的主控因素[5],针对此提出了巷道围岩控制的均衡屈服支撑理念[6],论证了采用锚喷[7-8]和锚注支护将利于应力向围岩深部的转移,喷浆层不仅封闭围岩,而且也具有自承载能力。锚喷对混凝土性能要求较高,而混凝土需要逐渐硬化从而达到设计强度[9],因此研究早龄期混凝土的力学性质是选择材料和判断最终支护效果的关键。
为此,相关学者利用设备营造出不同温度、不同湿度和不同单日温度变化的混凝土养护环境,探析环境变化对早龄期混凝土的影响[10];同时为了提高实验的可重复性,利用纯水泥石测试不同外加剂对其性能的影响[11]。但实际使用中的混凝土(或水泥石)始终处在应力环境下,为此研究人员通过单轴循环受压方式模拟深部巷道围岩应力,研究钢纤维混凝土循环受压性能,建立了钢纤维混凝土循环受压弹塑性损伤本构模型[12-13];在此基础上,通过单轴加卸载方式对模拟井壁混凝土能量演化进行了研究[14],利用振动试验系统开展了新浇混凝土爆破振动损伤累积模拟试验[15-17],同时利用SHPB二波法理论重构了混凝土试件的应力-应变曲线,分析了混凝土试件破坏规律[18-19]。同时也应看到,温度对混凝土(或水泥石)强度影响较大[20],对不同水温对水泥石劣化方式也进行了研究[21]。这些研究主要集中在对深部巷道混凝土的应用特性及损伤机制分析上,但是混凝土往往在未达到设计强度时就已经承受载荷,此时的损伤虽未造成破坏但其带来的变化切实存在,内部积累的塑性损伤会导致混凝土后期承载特性受到较大影响。
笔者通过对早期水泥石损伤特性理论分析,利用刚性试验机,对5组10个水泥石试件进行早期损伤单轴压缩与后期承载力学试验,分析了早期水泥石损伤机制及基本特性,确定了早期水泥石损伤阈值,研究了早期水泥石不同损伤对后期强度、变形的影响规律以及与弹性模量、泊松比的关系,提出了基于早期水泥石损伤的后期承载失稳模式。研究结果可为深部巷道围岩喷层参数选择提供依据。
1 早期水泥石损伤模型确定
1.1 早期水泥石损伤特征分析
水泥石在外力作用下会产生变形、失稳,且在抵抗外力时存在临界值,超过此值则丧失原有属性。从力学角度出发,水泥石完整结构是由多结构面互相铰接而成。在外力作用下,铰接键均匀受力,一旦外力超过某个铰接键临界值,便会丧失一部分铰接结构面,随着铰接键断裂数目增加,水泥石由损伤进入破裂状态,因此水泥石破坏过程可以理解为结构面铰接键断裂积累的集中表现(图1)。
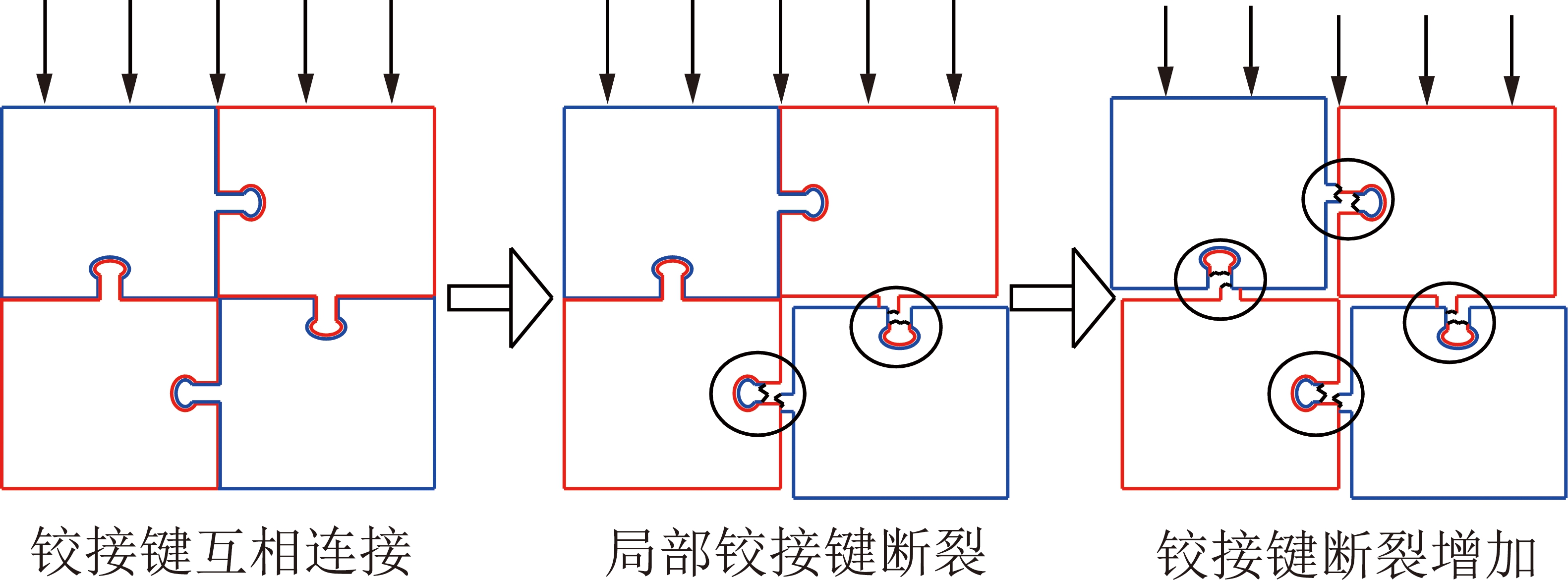
图1 铰接断裂示意
Fig.1 Hinged fracture diagram
早期水泥石试件进行单轴压缩试验可得到典型全应力-应变曲线(图2),包括空隙压密(OA段)、线弹性(AB段)、塑性(或屈服)(BC段)与破坏阶段(C点之后),很明显,早期水泥石试件应力-应变曲线与28 d龄期后的水泥石试件应力-应变曲线只存在线弹性(或部分线弹性)、塑性(屈服)与破坏阶段是截然不同的。
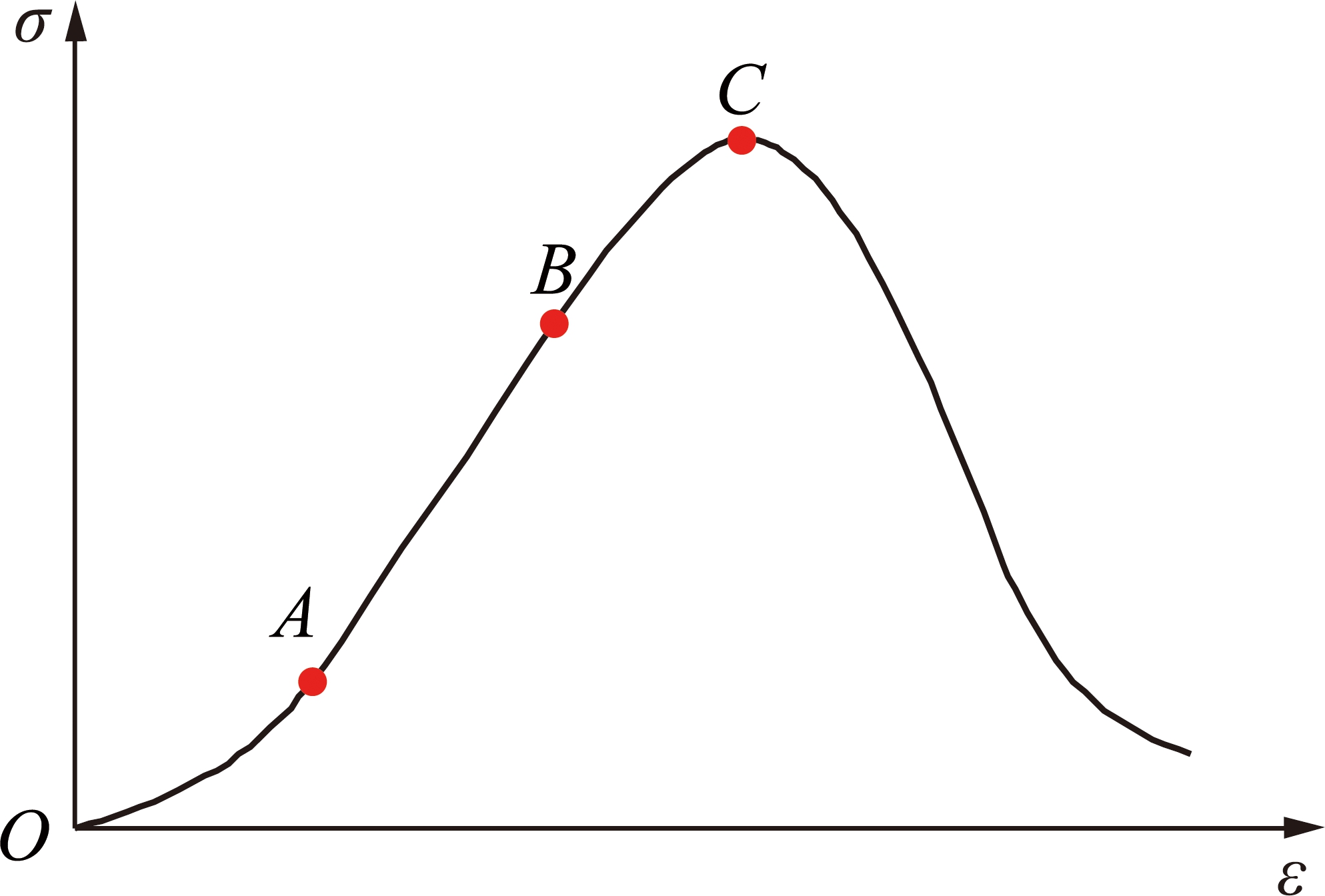
图2 典型全应力-应变曲线
Fig.2 Full typical stress-strain curve
1.2 早期水泥石损伤方程构建
为准确表述早期水泥石试件的损伤特性,依据早期水泥石试件全应力-应变曲线特征,将早期水泥石试件应力-应变曲线分为2段进行考虑,即在曲线上任意点做切线,当某点切线可将破坏前应力-应变曲线(OC段)划分为上下2段时确定此点为分界点(G点),如图3所示。GC段与常规水泥石(28 d龄期后)应力应变曲线一致,采用常规损伤方程进行损伤量计算;OG段为早期水泥石独有特性,据此构建水泥石全应力-应变曲损伤方程。
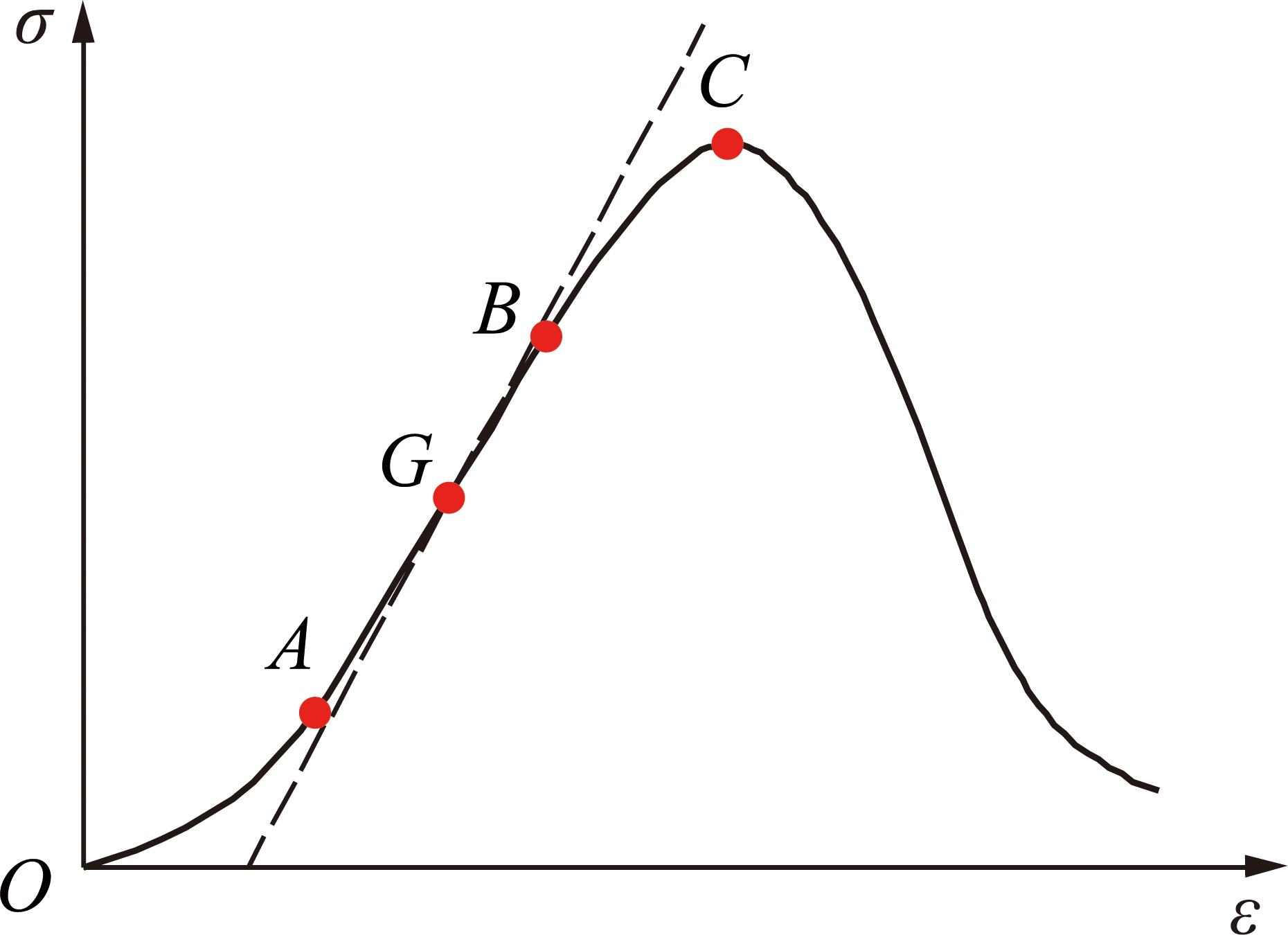
图3 应力-应变曲线
Fig.3 Stress-strain curve
由于常规损伤方程的损伤起点为0,而在早期水泥石试件中G点不可能为0,且G点损伤量由水泥石水灰比确定,因此,为适应不同早期水泥石试件损伤特性,这里引入损伤系数k(由水对水泥石弹性起表现作用的比例决定),则GC段水泥石试件损伤方程为
![]()
(1)
式中,D2为损伤系数在k~1时的损伤量;EC为早期水泥石试件应力-应变曲线不同位置切线模量,MPa;ED为早期水泥石试件弹性模量(这里取G点切线模量),MPa;k为早期水泥石试件损伤系数。
在早期水泥石试件应力-应变曲线OG阶段,同样引入损伤系数k,且要求前段损伤与后段损伤在对接G点损伤量相等。则可构建OG阶段水泥石试件损伤方程为
![]()
(2)
式中,D1为损伤系数在0~k时的损伤量。
依据早期水泥石试件单轴压缩全应力-应变曲线特征,构建具有全应力-应变曲线各阶段特征早期水泥石试件完整损伤模型方程为
![]()
(3)
据此式对试件进行计算,绘制损伤量曲线(图4)。可以看出,损伤曲线共可分为3个阶段:
(1)压密损伤段(OA段)。在开始加载后水泥石内部空隙随荷载增大而不断缩小闭合,表现为损伤量急速上升。
(2)损伤累积段(AB段)。在内部空隙压密后,水泥石进入弹性阶段,此时弹性模量小幅增加,水泥石内部无裂隙产生,表现为损伤量缓慢增加趋势。
(3)损伤爆发段(BC段)。荷载的持续增大使得内部损伤达到质变,不断萌生裂隙并逐渐相互贯通,在试件表面显现,水泥石在短时间内丧失承载能力,表现为损伤量上升骤然加快至破坏。
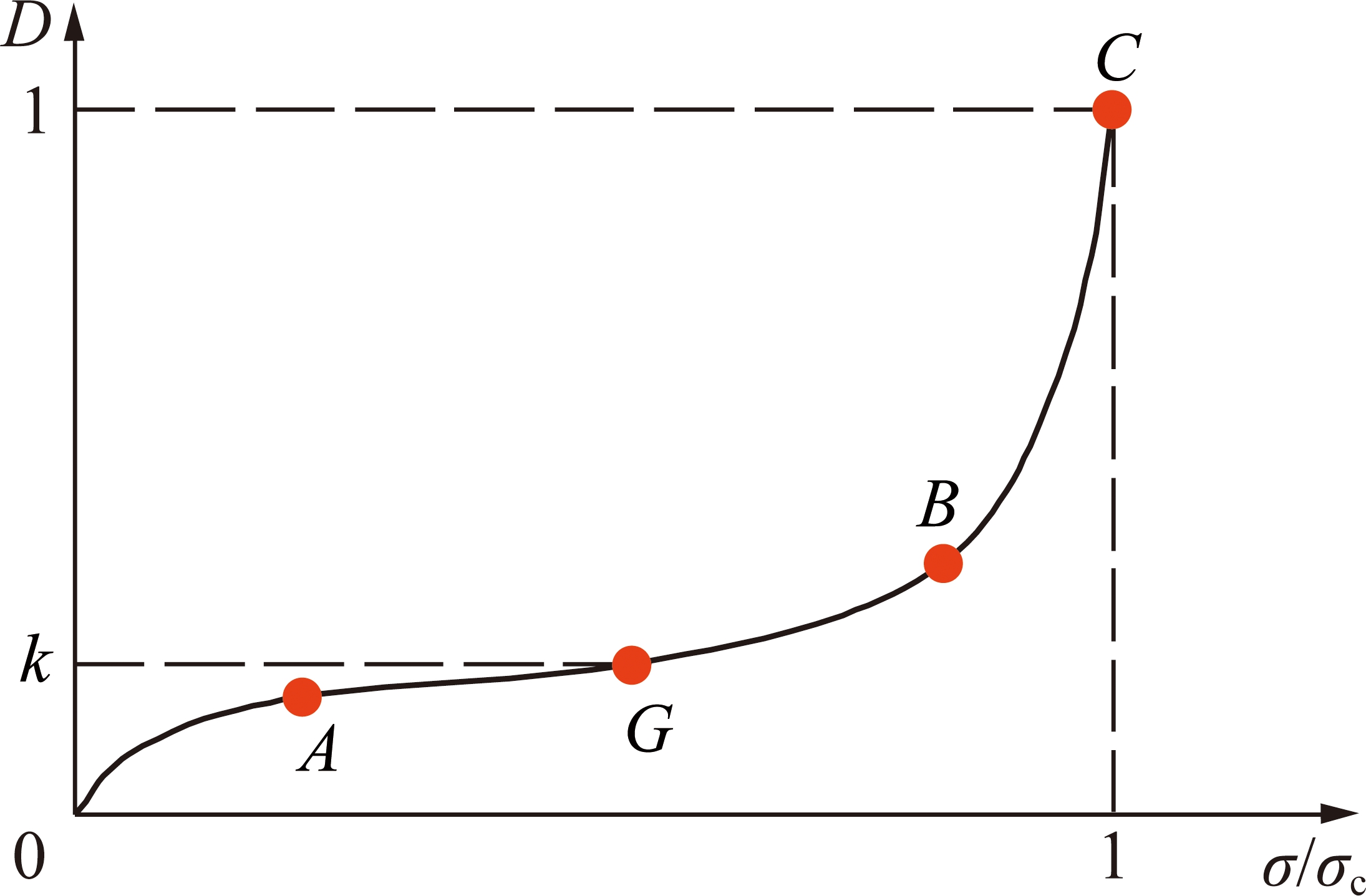
图4 损伤量曲线
Fig.4 Damage amount curve
2 水泥石单轴压缩试验
2.1 基础试件制作
制作水泥石试件选用坚固牌C32.5R硅酸盐水泥,为达到试件均质性不添加任何骨料,无外加剂,使用精度0.1 g电子秤进行水泥与清水质量比为3∶1的称重,试件装填模具采用标准规格100 mm×100 mm×100 mm三联模具进行水泥石试件装填(图5)。

图5 水泥石制样模具
Fig.5 Cement specimen mold
水泥石试件在自然条件下晾干24 h后脱模,并裸露在自然环境下3 d,加载端面采用细砂人工打磨至规定标准。三联模具每次制作3个试件作为1组,共制作5组15个试件(图6),组号为A,B,C,D,E,编号为A1,A2,A3,B1,B2,B3,……。

图6 水泥石试件制备成型
Fig.6 Preparation of cement specimens
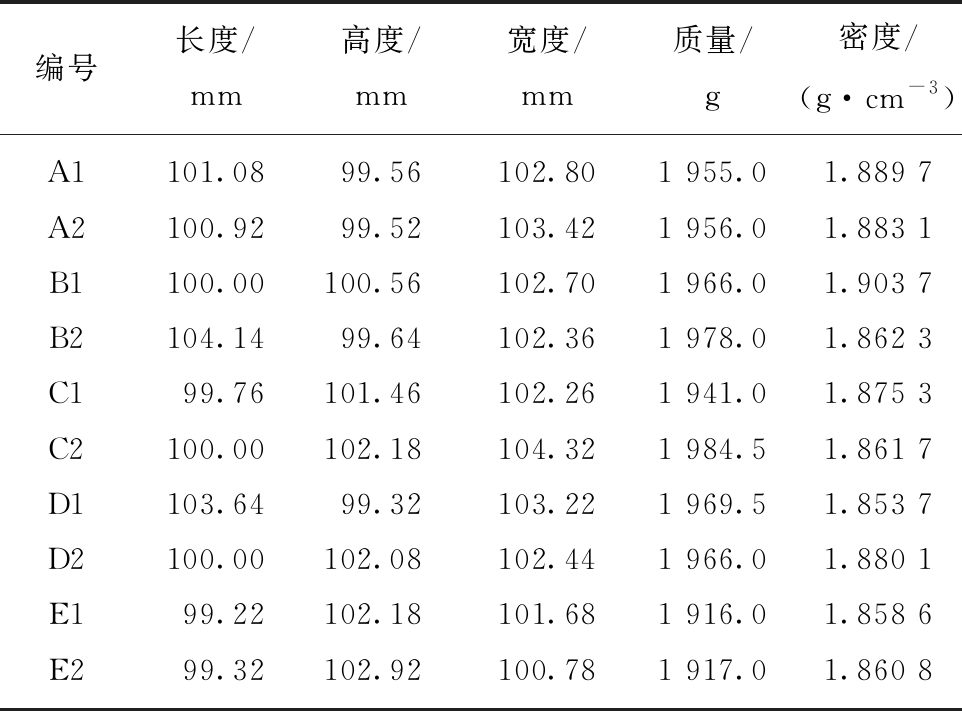
由于水泥石硬化过程存在析水现象,为保证试验均质性,每组选择完整性差异较小的2块试件(重新编号A1,A2,B1,B2,……)进行水泥石早期损伤单轴压缩试验,试件基本参数见表1。
2.2 早期损伤试验设计
根据已有文献[22]可知早期水泥石试件全应力-应变曲线中屈服点在80%应力点附近,为探究不同载荷对早期水泥石试件的损伤影响,设计A组早期水泥石试件进行单轴压缩试验,并以A组早期水泥石试件强度的85%,80%,75%,0%分别进行早期水泥石不同应力比(设计加载应力与早期水泥石试件破坏应力的比值)损伤试件B,C,D,E组的制作,加上100%破坏损伤试件(A组),共5组10个早期水泥石损伤试件。
2.3 后期承载试验设计
将早期水泥石不同应力比损伤试件在自然条件下放置到28 d龄期后进行后期单轴压缩试验。具体试验设计为:首先,保留试件脱落部分,使用刷子轻轻将试件加载端面清理干净后放置在试验机加载盘中心,搭载轴向、横向数字千分表;其次,采用位移加载方式,试验初始载荷1 kN、加载速率为0.02 mm/s,利用数字千分表采集试件轴向、横向变形,加载至试件破坏。
表1 水泥石试件基本特征
Table 1 Basic parameters of cement specimens
编号长度/mm高度/mm宽度/mm质量/g密度/(g·cm-3)A1101.0899.56102.801 955.01.889 7A2100.9299.52103.421 956.01.883 1B1100.00100.56102.701 966.01.903 7B2104.1499.64102.361 978.01.862 3C199.76101.46102.261 941.01.875 3C2100.00102.18104.321 984.51.861 7D1103.6499.32103.221 969.51.853 7D2100.00102.08102.441 966.01.880 1E199.22102.18101.681 916.01.858 6E299.32102.92100.781 917.01.860 8
3 早期水泥石损伤特性
水泥石早期损伤单轴压缩试验应力-应变曲线如图7所示,试件单轴压缩试验数据见表2。
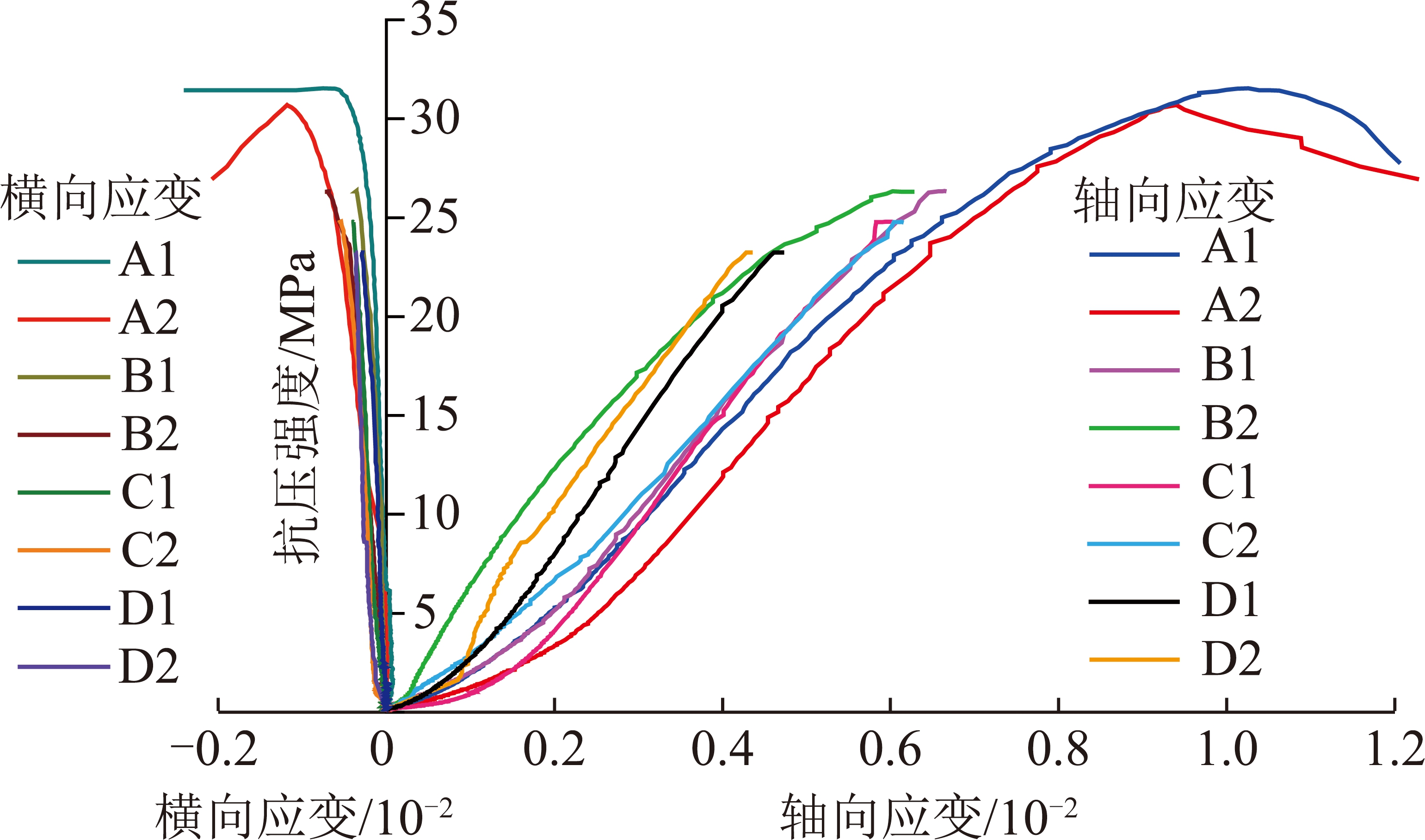
图7 试件单轴压缩应力-应变曲线
Fig.7 Uniaxial compressive stress-strain curves
表2 水泥石早期损伤单轴压缩试验数据
Table 2 Uniaxial compression test data of the early damage cement
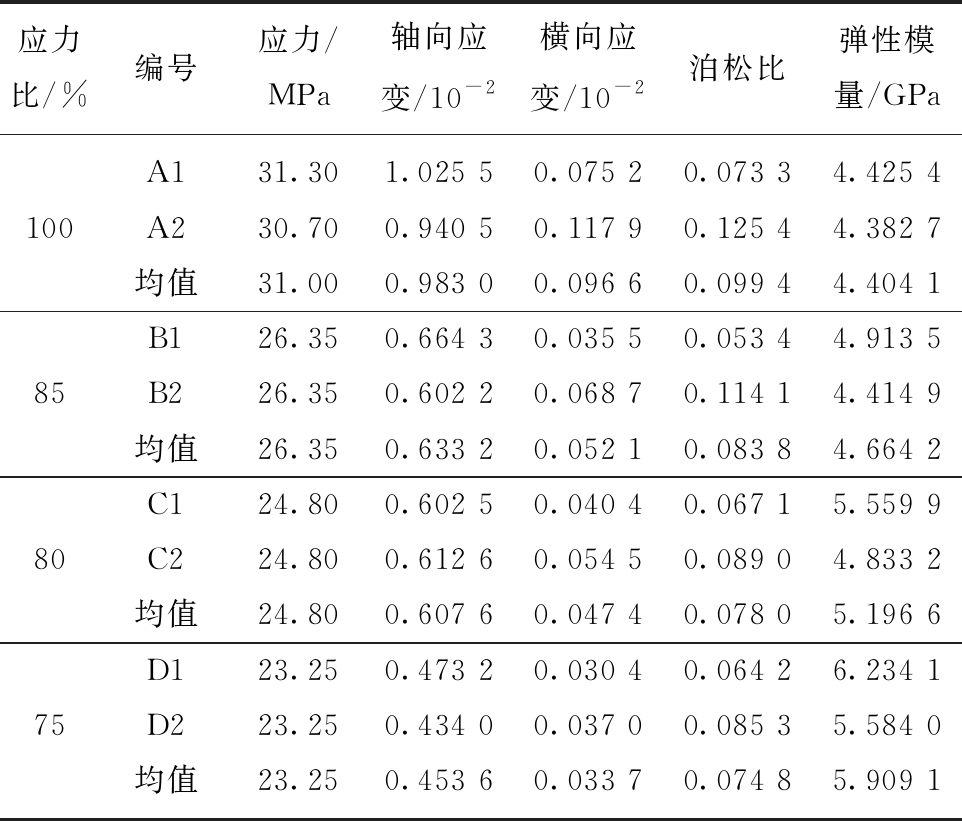
应力比/%编号应力/MPa轴向应变/10-2横向应变/10-2泊松比弹性模量/GPaA131.301.025 50.075 20.073 34.425 4100A230.700.940 50.117 90.125 44.382 7均值31.000.983 00.096 60.099 44.404 1B126.350.664 30.035 50.053 44.913 585B226.350.602 20.068 70.114 14.414 9均值26.350.633 20.052 10.083 84.664 2C124.800.602 50.040 40.067 15.559 980C224.800.612 60.054 50.089 04.833 2均值24.800.607 60.047 40.078 05.196 6D123.250.473 20.030 40.064 26.234 175D223.250.434 00.037 00.085 35.584 0均值23.250.453 60.033 70.074 85.909 1
3.1 早期水泥石试件损伤特征
依据早期水泥石损伤计算式(3)(考虑到水泥石基本损伤特性(水灰比不同),这里损伤系数取k=0.25)可得早期水泥石试件损伤量(表3)。
表3 不同应力比损伤量
Table 3 Damage parameters in different stress ratio
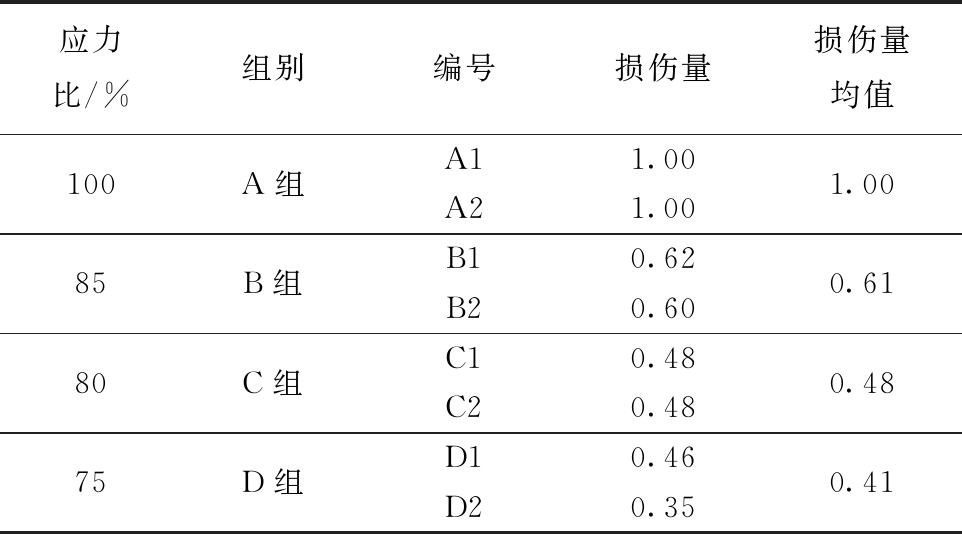
应力比/%组别编号损伤量损伤量均值100A组A11.00A21.001.0085B组B10.62B20.600.6180C组C10.48C20.480.4875D组D10.46D20.350.41
绘制不同应力比加载水泥石试件损伤量曲线(图8),可以看出各组水泥石试件损伤量曲线趋势相仿,且呈现出明显的增长趋势;在水泥石早期损伤单轴压缩试验中,因试件存在差异使得损伤量曲线终值略有不同。
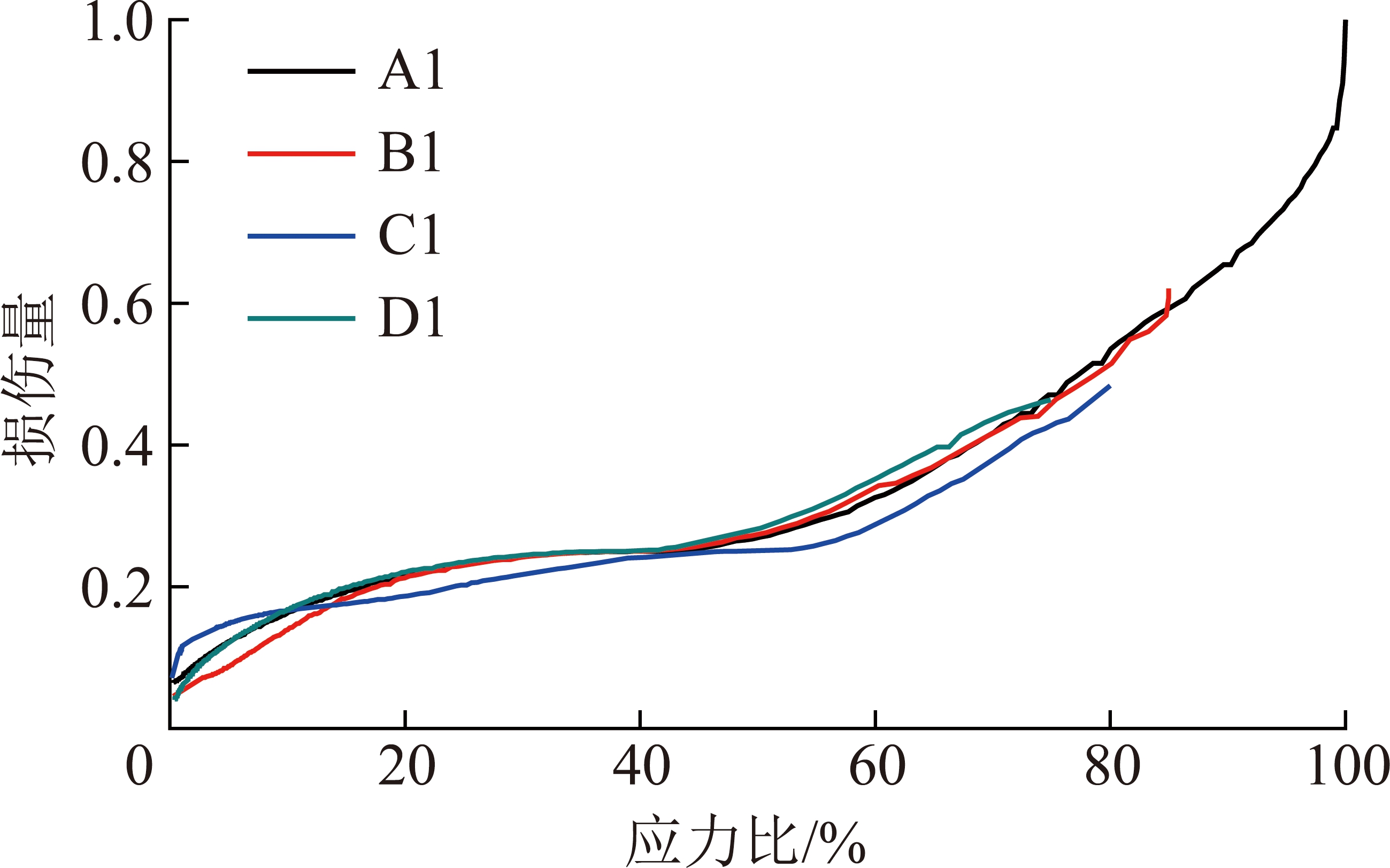
图8 应力比与部分损伤曲线关系
Fig.8 Relationship between stress ratio and partial damage curves
对于早期水泥石试件应力比与损伤量关系(图9),应力比从75%增加到80%,早期水泥石试件损伤量从0.41增加到0.48,增幅17.07%;应力比从80%增加到85%,早期水泥石试件损伤量从0.48增加到0.61,增幅27.08%;应力比从85%增加到100%,早期水泥石试件损伤量从0.61增加到1.00,增幅63.93%。很明显,早期水泥石试件在75%~85%应力比区间内存在转折点,结合图8亦可明显得知,早期水泥石试件在80%应力比(损伤量为0.48)后上升趋势增加,损伤阈值明显。
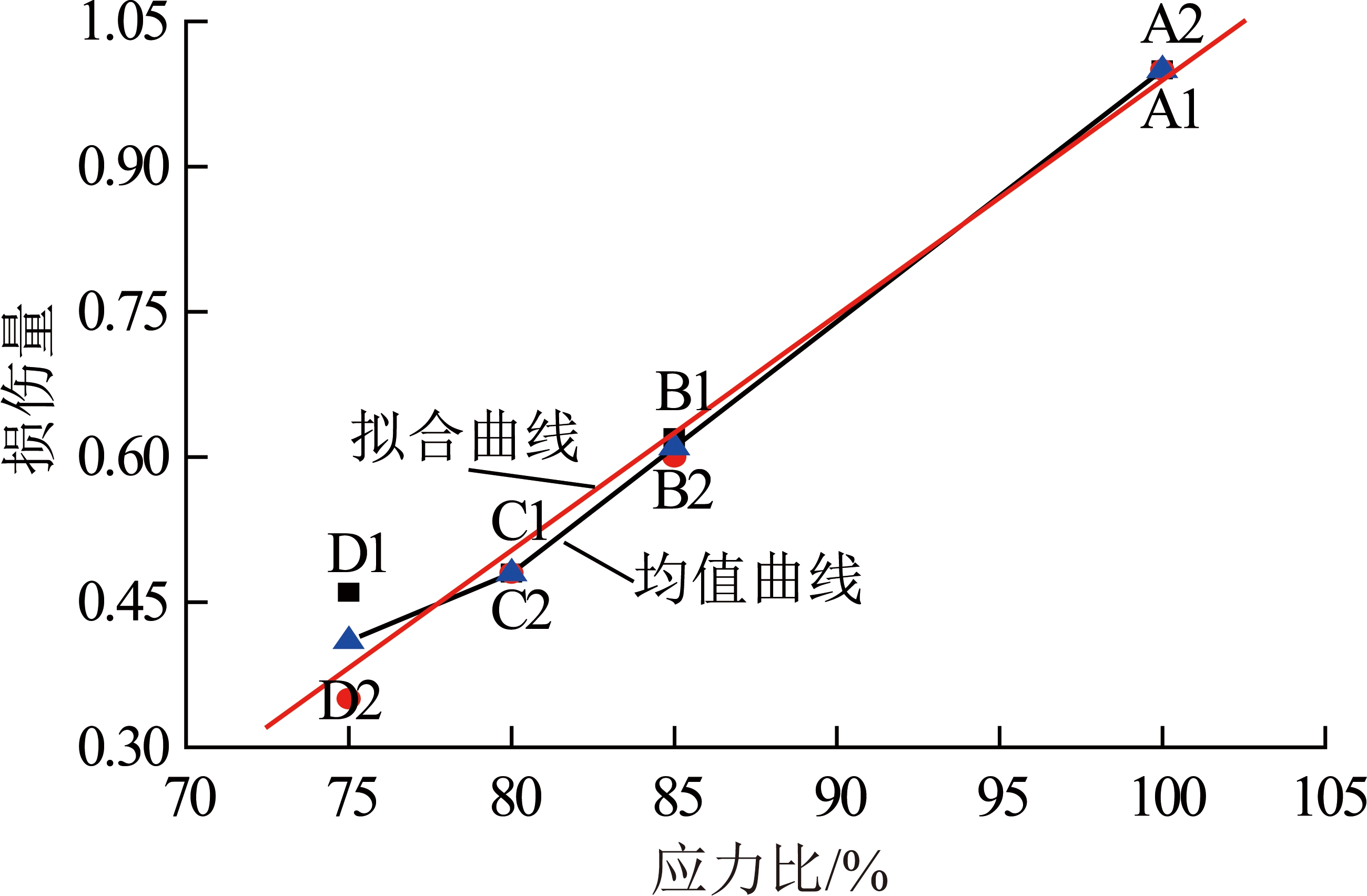
图9 应力比与损伤量关系
Fig.9 Relationship between stress ratio and damage amount
将应力比与损伤量关系进行线性拟合,则可得
D=0.024 29σx-1.439 29
(4)
式中,D为早期水泥石试件的损伤量;σx为早期水泥石试件应力比(75%~100%)。
相关性系数为R2=0.992 0,线性函数式可以表征早期水泥石试件应力比与损伤量关系。
3.2 应力比与轴向应变、横向应变关系
水泥石试件在3 d龄期单轴压缩破坏过程中经历压密阶段、弹性阶段、塑性阶段与破坏阶段,同组损伤水泥石试件横向应变小于轴向应变,荷载终值越大,轴向变形与横向变形越明显。早期水泥石试件应力比越大,试件应力-应变曲线的上翘趋势越明显,相同应变条件下应力越大。
随着应力比(75%~100%)增加,水泥石试件应变终值同步增加,轴向应变终值大于横向应变终值(图10)。当应力比从75%增加到85%,轴向应变终值均值由0.453 6×10-2增加到0.633 3×10-2,增幅39.62%,而横向应变终值均值由0.033 7×10-2逐渐增加到0.052 1×10-2,增幅达54.60%,横向应变增幅大于轴向应变,但轴向变形对于荷载增加表现更加直观。
对不同应力比与轴向应变关系进行拟合,可得
εD1=0.020 49σx-1.072 18
(5)
式中,εD1为早期水泥石试件轴向应变,10-2。
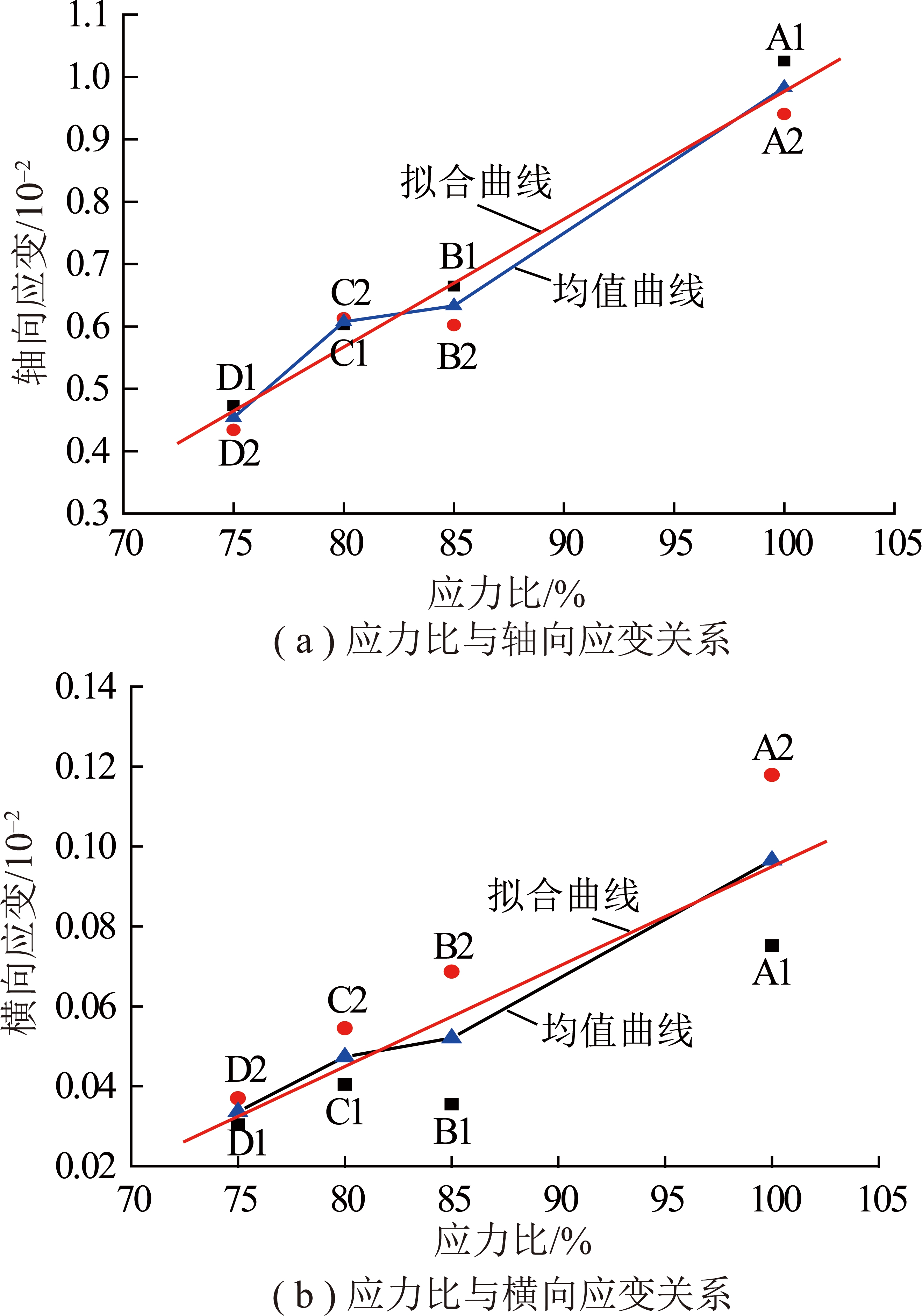
图10 不同应力比与应变关系
Fig.10 Relationships between different stress ratio and the strain
对不同应力比与横向应变关系进行拟合,则可得
εD2=0.002 5σx-0.155 05
(6)
式中,εD2为早期水泥石试件横向应变,10-2。
应力比与轴向、横向应变关系的相关性系数分别为R2=0.979 3,R2=0.982 5,表明线性函数式可以较好地表征水泥石试件应力比与轴向、横向应变关系。
以75%应力比早期水泥石试件应变终值作为基准,计算其他组试件相对75%应变终值比率及各组相对前一组应变终值比率,并绘制曲线(图11)。
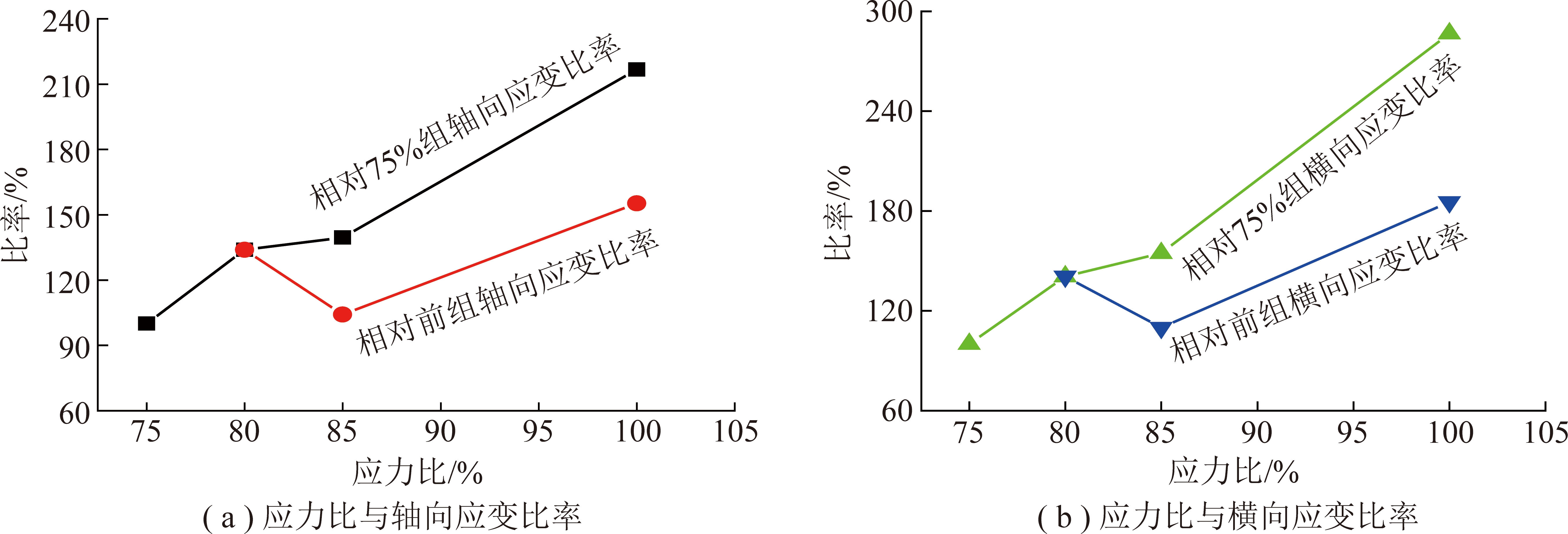
图11 应力比与应变均值比率关系
Fig.11 Relationships between stress ratio and strain mean
由图11可知,随着应力比(75%~100%)增加,相对于75%应力比组水泥石试件轴向与横向应变均值呈增加趋势,横向应变均值比率分别为140.65%,154.60%,286.65%,轴向应变均值比率为133.95%,139.59%,216.71%,早期水泥石试件横向应变比率大于轴向应变比率。
整体上,4条曲线应力比从80%到85%过程中,水泥石试件横向与轴向应变比率呈衰减趋势,表明水泥石试件开始进入弹性阶段过程,而应力比超过85%后,水泥石试件横向与轴向应变比率进入加速增加阶段,表明水泥石试件进入屈服阶段产生裂隙贯通并最终失稳。
3.3 应力比与泊松比、弹性模量关系
对于早期水泥石试件不同应力比与泊松比关系,由图12可以看出,随着应力比增加,水泥石损伤试件泊松比呈增加趋势,水泥石试件应力比从75%增加至100%过程中,不同损伤水泥石试件泊松比均值分别为0.074 8,0.078 0与0.083 8与0.099 4,增幅分别为4.28%,7.44%与18.62%,水泥石试件应力比与泊松比具有正线性相关性。
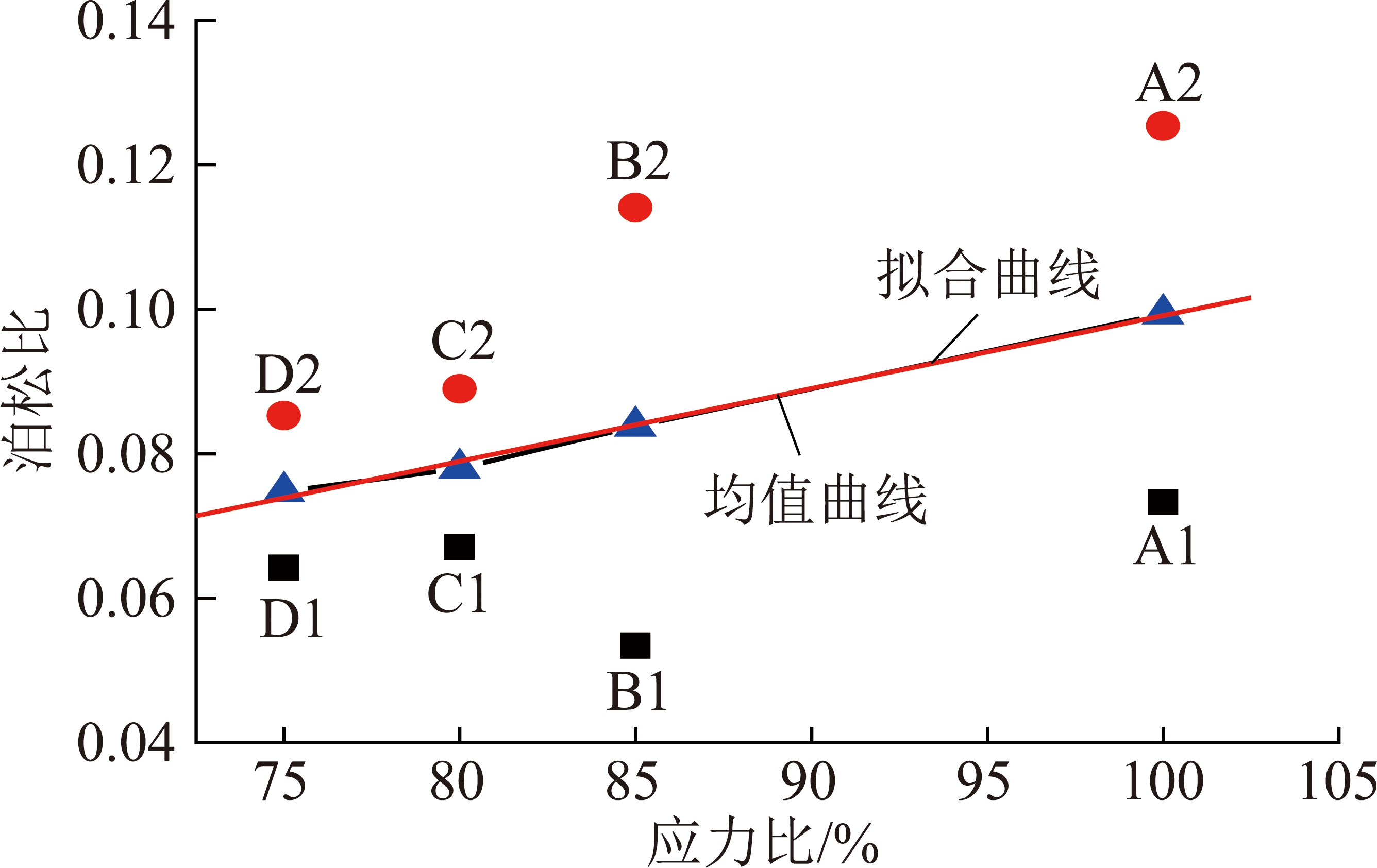
图12 不同应力比与泊松比关系
Fig.12 Relationship between different stress ratios and Poisson’s ratio
对不同应力比与早期水泥石试件泊松比关系进行拟合,则可得
μD=0.001 01σx-0.001 73
(7)
式中,μD为早期水泥石试件泊松比。
相关性系数为R2=0.995 0,线性函数式可以较好表征水泥石试件应力比与泊松比关系。
对于早期水泥石试件弹性模量,这里选取应力-应变曲线中近直线段进行计算得到试件弹性模量(图13)。
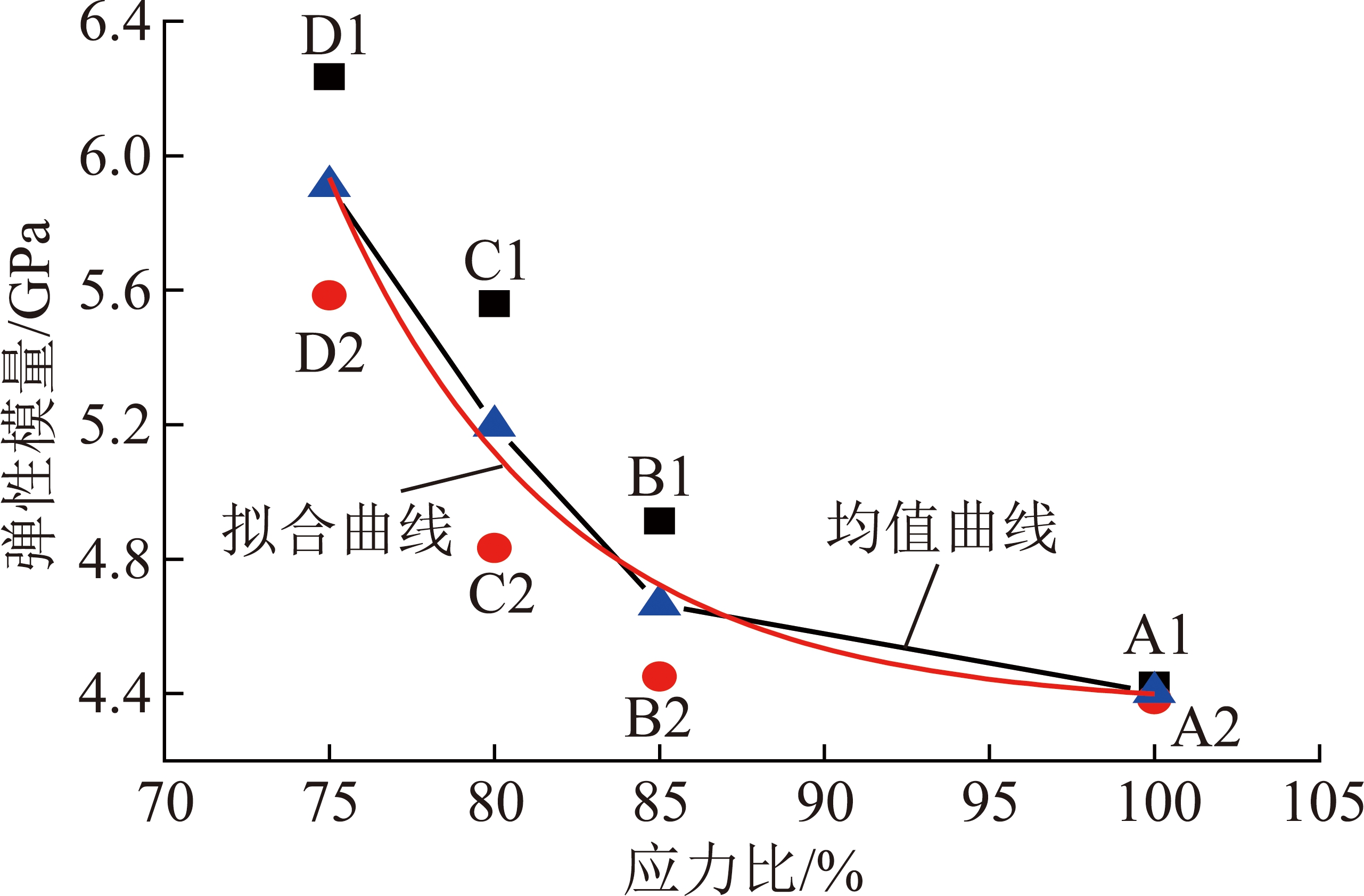
图13 不同应力比与弹性模量关系
Fig.13 Relationship between different stress ratios and elastic modulus
可以看出,随着应力比增加,水泥石损伤试件弹性模量呈衰减趋势。水泥石试件应力比从75%增加至100%过程中,不同损伤水泥石试件弹性模量均值分别为5.909 1,5.196 6,4.664 2与4.404 1 GPa,减幅分别为12.06%,10.25%与5.58%,整体呈负指数衰减趋势。
对不同应力比与水泥石试件弹性模量关系进行拟合,则可得
![]()
(8)
式中,ED为早期水泥石试件弹性模量,GPa。
相关性系数为R2=0.992 1,负指数函数式可以表征早期水泥石试件不同应力比与弹性模量关系。对比不同应力比损伤水泥石试件的泊松比与弹性模量,可以很明显的看出,泊松比与弹性模量作为早期水泥石试件的固有属性,在试件损伤后呈现不同的特征,表明损伤对水泥石试件内部结构产生重要影响。
4 后期承载特征与失稳模式
水泥石试件后期单轴压缩试验应力-应变曲线如图14所示,水泥石试件后期单轴压缩试验数据见表4。
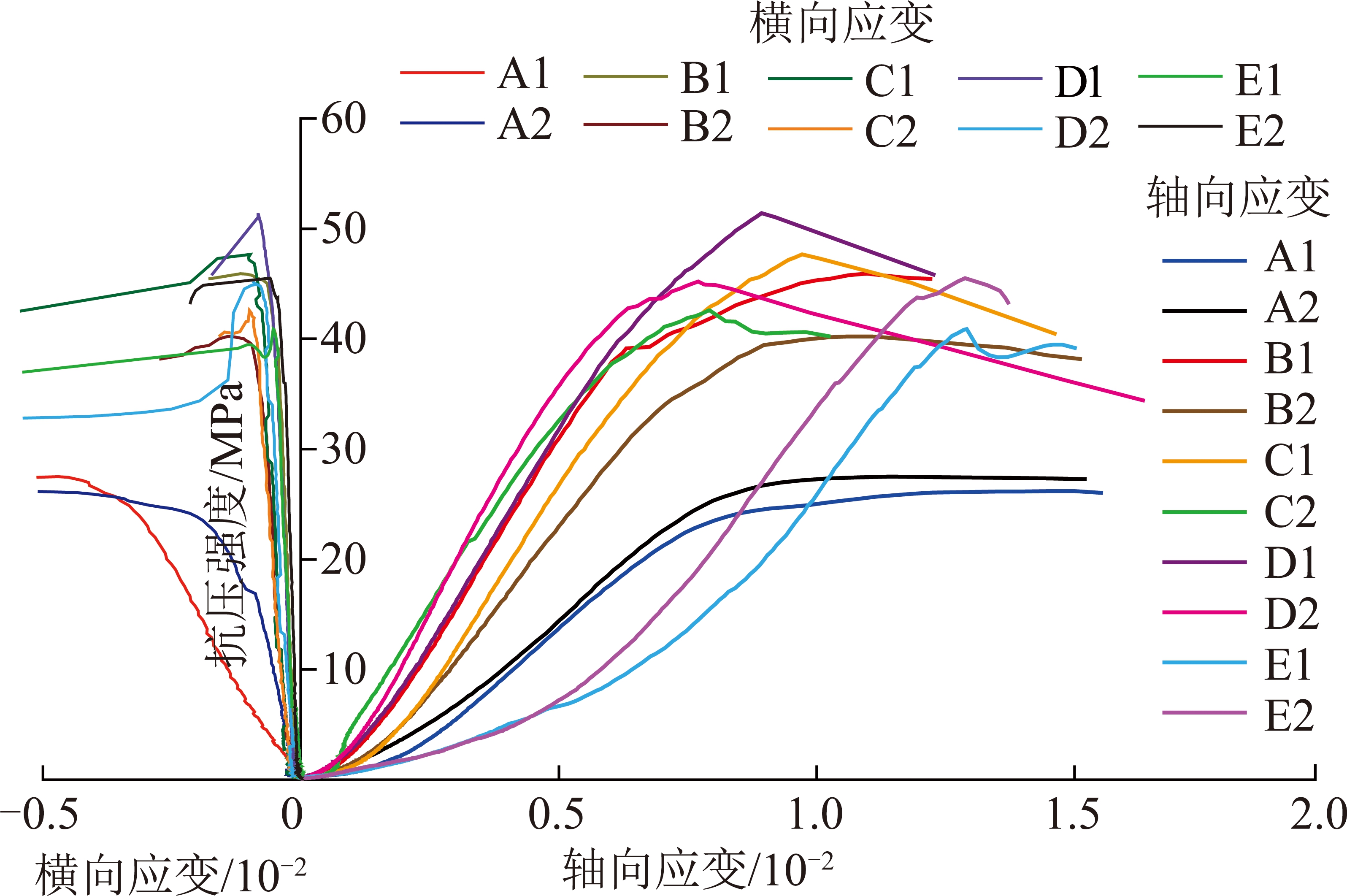
图14 损伤试件单轴压缩全应力-应变曲线
Fig.14 Full uniaxial compression stress-strain curves of damage specimen
4.1 早期损伤与后期强度、变形关系
水泥石试件在损伤后再次进行单轴压缩试验所得到的全应力-应变曲线与E组(无损伤组)曲线存在明显不同。损伤试件空隙裂隙压密阶段极短甚至不存在,并且在试件破坏后承载能力并不表现为瞬间丧失,而是以线性方式缓慢丧失,且早期损伤量越高的试件丧失越为平缓,各组水泥石试件轴向破坏应变大于横向破坏应变。
由图15及表5可明显看出,早期水泥石试件不同损伤程度对后期抗压强度影响显著;早期完全破坏的水泥石试件由于内部水化反应的持续存在,使得后期仍具备一定的承载能力;随着早期水泥石试件损伤程度增大,后期水泥石试件单轴抗压强度先呈增加趋势后呈衰减趋势,水泥石早期损伤量由0增加到0.41,后期水泥石试件强度由43.210 9 MPa提高到48.304 5 MPa,增幅11.79%,损伤量由0.41增加到1.00,后期水泥石试件强度从48.304 5 MPa衰减到26.845 8 MPa,衰减幅度为44.42%,单轴抗压强度衰减幅度大于增加幅度。
表4 后期水泥石单轴压缩破坏试验数据
Table 4 Data on late cement uniaxial compressive failure test
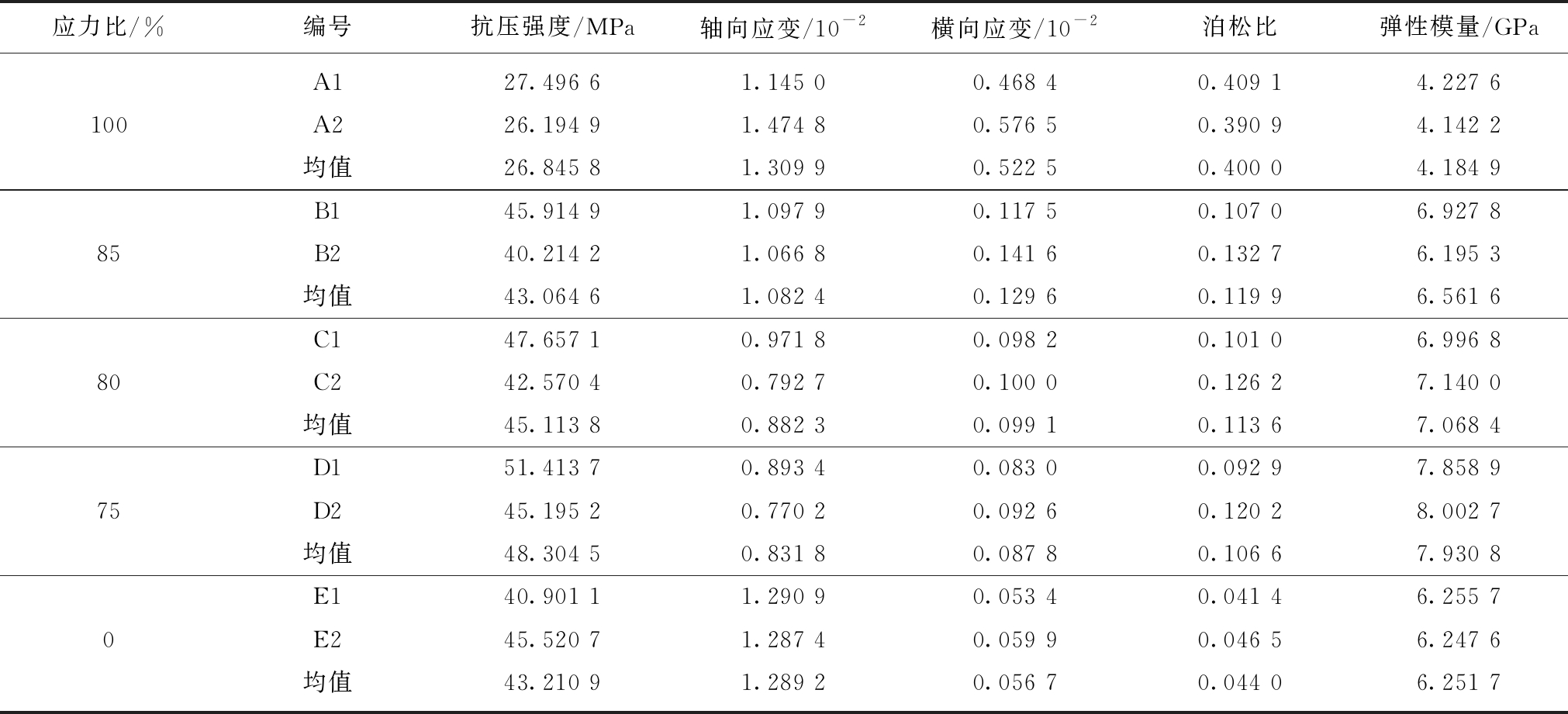
应力比/%编号抗压强度/MPa轴向应变/10-2横向应变/10-2泊松比弹性模量/GPaA127.496 61.145 00.468 40.409 14.227 6100A226.194 91.474 80.576 50.390 94.142 2均值26.845 81.309 90.522 50.400 04.184 9B145.914 91.097 90.117 50.107 06.927 885B240.214 21.066 80.141 60.132 76.195 3均值43.064 61.082 40.129 60.119 96.561 6C147.657 10.971 80.098 20.101 06.996 880C242.570 40.792 70.100 00.126 27.140 0均值45.113 80.882 30.099 10.113 67.068 4D151.413 70.893 40.083 00.092 97.858 975D245.195 20.770 20.092 60.120 28.002 7均值48.304 50.831 80.087 80.106 67.930 8E140.901 11.290 90.053 40.041 46.255 70E245.520 71.287 40.059 90.046 56.247 6均值43.210 91.289 20.056 70.044 06.251 7
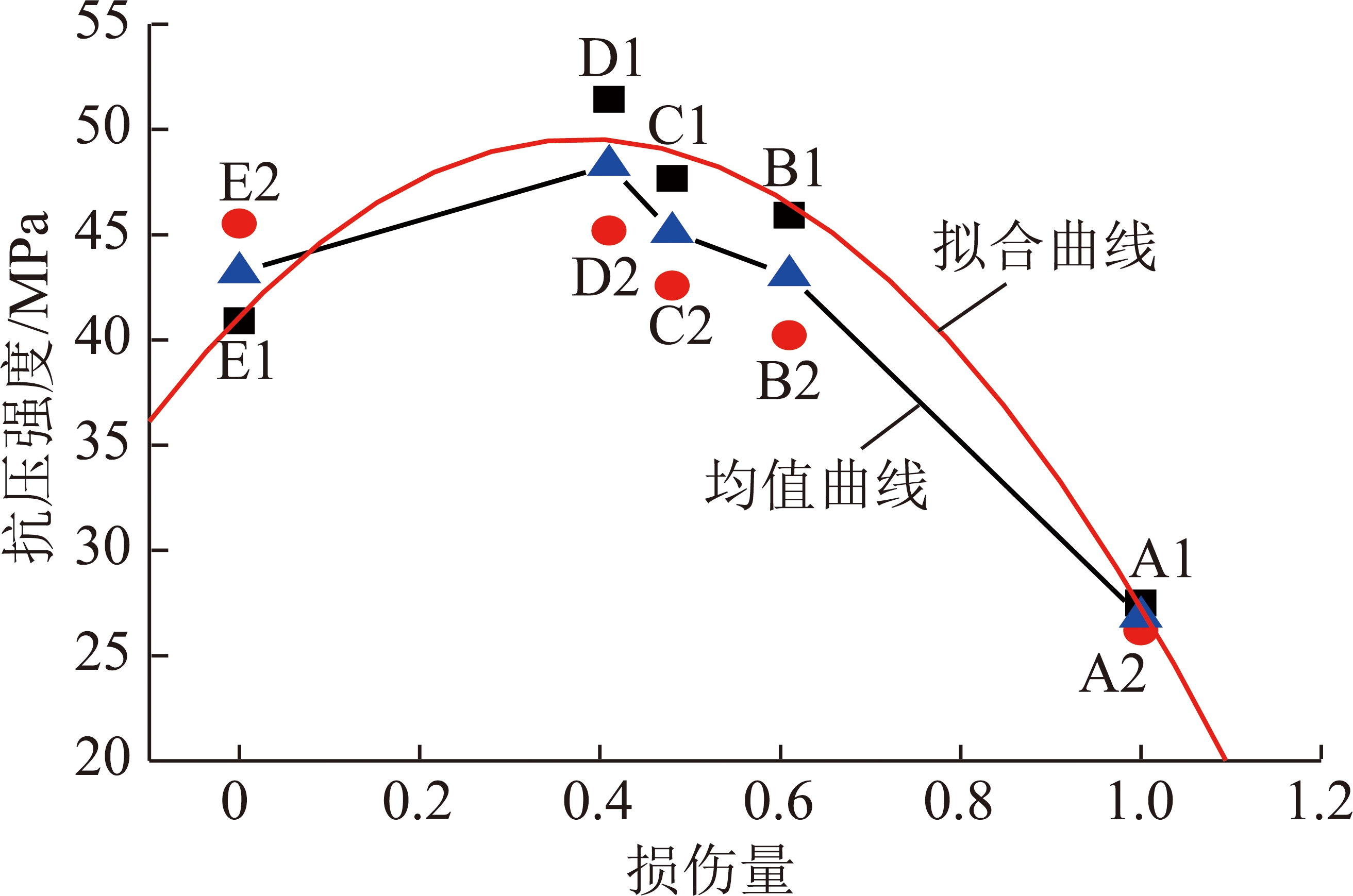
图15 损伤量与抗压强度关系
Fig.15 Relationship between damage amount and compressive strength
表5 损伤量与抗压强度
Table 5 Damage amount and compressive strength
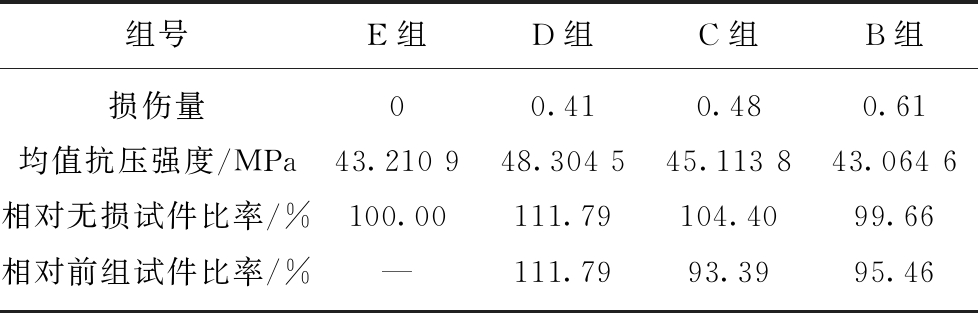
组号E组D组C组B组损伤量00.410.480.61均值抗压强度/MPa43.210 948.304 545.113 843.064 6相对无损试件比率/%100.00111.79104.4099.66相对前组试件比率/%—111.7993.3995.46
对不同损伤量与单轴抗压强度关系进行拟合,则可得
σc=41.127 7+44.179 3D-58.004 7D2
(9)
式中,σc为后期水泥石试件单轴抗压强度,MPa。
相关性系数为R2=0.983 1,二次多项式可以较好地表征试件水泥石早期损伤量与后期单轴抗压强度的关系。
应注意的是,损伤量为0.41与0.48时,水泥石试件破坏强度大于无损伤试件破坏强度,表明早期水泥石试件受较小损伤会提高试件后期强度,而损伤量在0.61时,水泥石试件破坏强度小于无损伤试件强度,表明损伤达到一定值(损伤阈值)后,水泥石试件早期损伤会降低后期强度,研究结果与魏建军等[22]、蒋正武等[23]的研究结果相符。
由水泥石试件损伤量与强度比率关系(图16)可以看出,随着水泥石试件早期损伤量的增加,后期水泥石试件强度比率也呈先增加后减小趋势,表明水泥石早期不同程度损伤对后期水泥石试件会产生强度增强与强度衰减2种影响。当早期水泥石试件损伤量导致后期水泥石试件出现由强度增强向强度衰减过渡时,此早期水泥石损伤量可确定为早期水泥石损伤阈值,这也印证了早期水泥石损伤方程分析的合理性。
对于不同损伤量与后期试件轴向变形关系,由图17(a)可以看出,随着早期水泥石试件损伤量增加,水泥石试件轴向应变表现为先减小后增加趋势。由于无损水泥石(E组)存在空隙压密阶段,所以轴向应变较大,而完全损伤试件(A组)内部已然裂隙密布,同样使得轴向变形较大,除此之外的其余各组试件随着水泥石试件早期损伤量的增加(0.41~0.61)试件峰值轴向应变随之增大。整体上,损伤量从0.41增加到0.48,轴向应变均值由0.831 8×10-2增加到0.882 3×10-2,增幅6.07%,损伤量从0.48增加到0.61,轴向应变均值由0.882 3×10-2增加到1.082 4×10-2,增幅22.68%,损伤量从0.61增加到1.00,轴向应变均值由1.082 4×10-2增加到1.309 9×10-2,增幅21.02%。
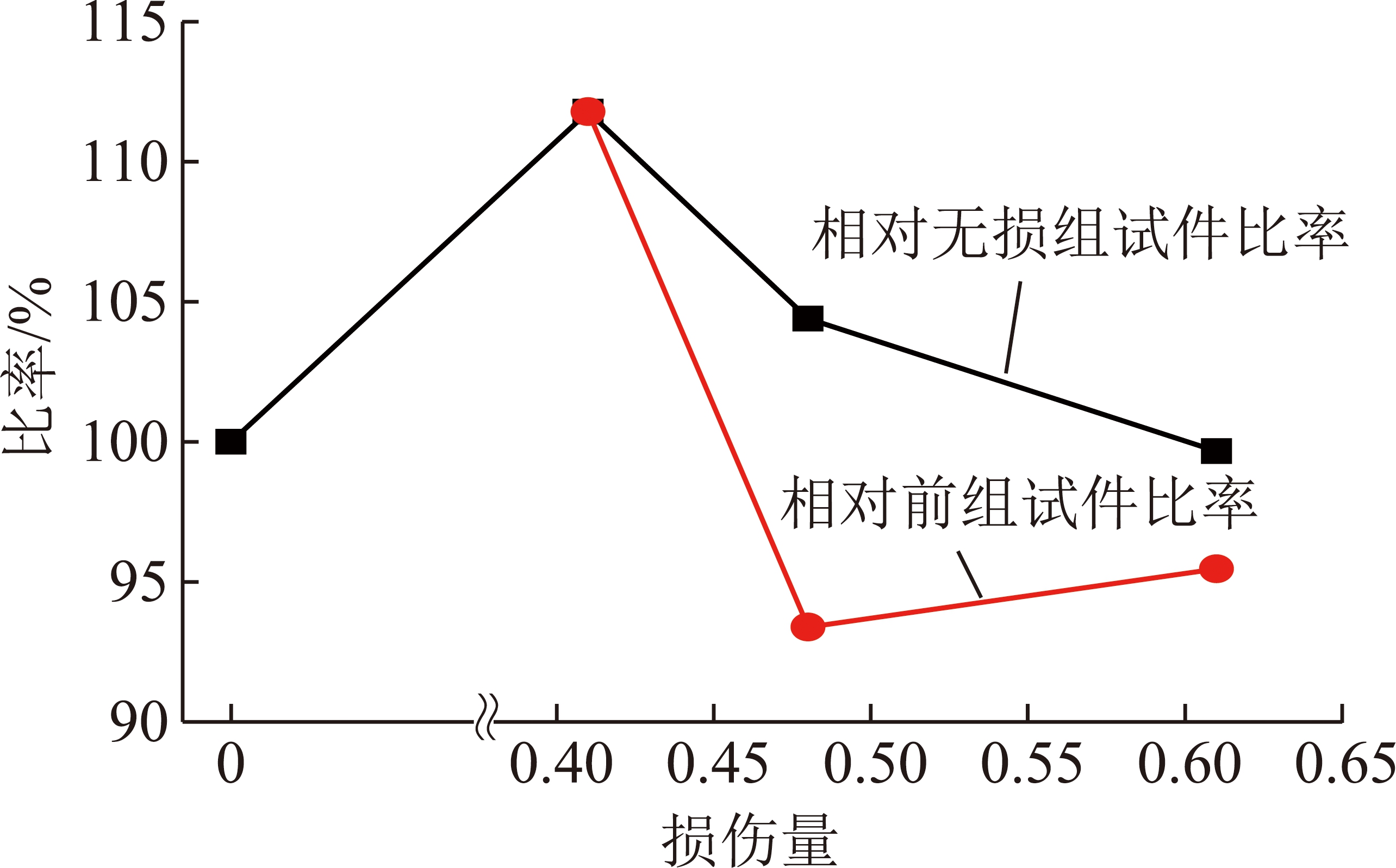
图16 损伤量与抗压强度比率关系
Fig.16 Relationship between damage amount and compressive strength
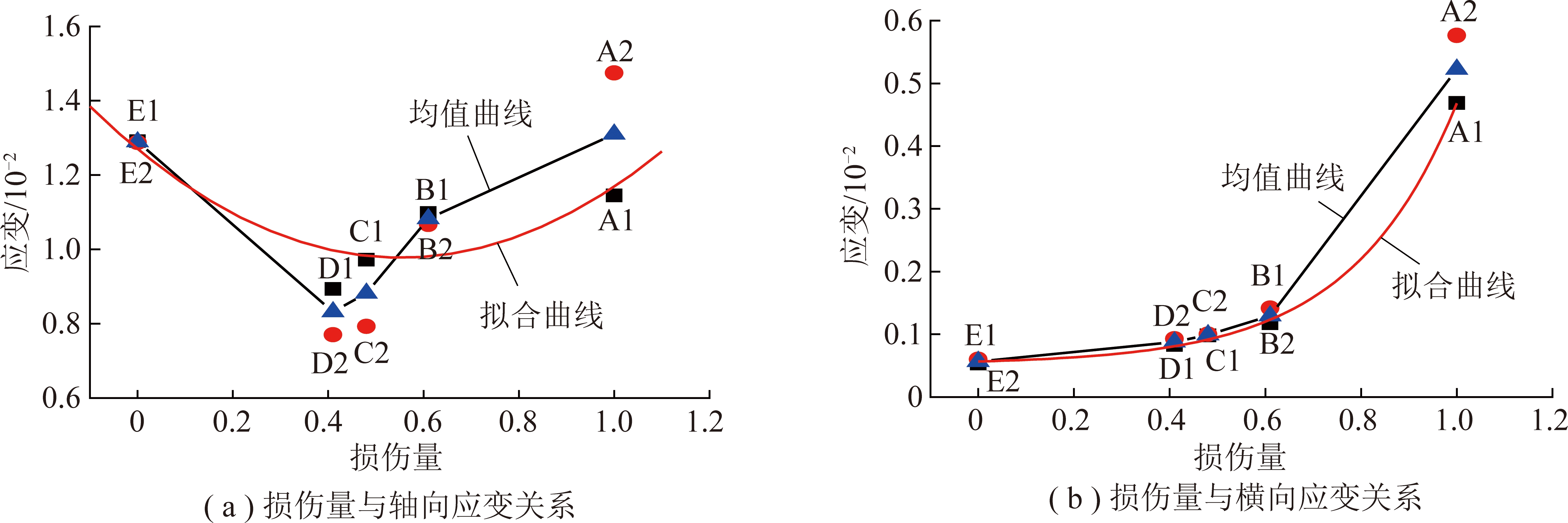
图17 损伤量与应变关系
Fig.17 Relationships between damage amount and the strain
对不同损伤量与轴向应变关系进行拟合,可得
ε1=1.269 6-1.055 9D+0.954 9D2
(10)
式中,ε1为后期水泥石试件轴向应变,10-2。
相关性系数为R2=0.731 9,表明采用二次多项式表征试件不同损伤量与试件轴向应变的关系较差。当然,可以看出,损伤虽然对试件有一定压密作用,减小了后期压缩的变形,但损伤程度超过阈值,压密段终止进入屈服段,后期压缩轴向变形出现陡增。
对于不同损伤量与后期试件横向变形关系,由图17(b)可以看出,随着早期水泥石试件损伤量增加,水泥石试件横向应变表现为缓慢增加到急速增加趋势,损伤量从0增加到0.41,横向应变均值由0.056 7×10-2增加到0.087 8×10-2,增幅54.85%,损伤量从0.41增加到0.48,横向应变均值由0.087 8×10-2增加到0.099 1×10-2,增幅12.87%,损伤量从0.48增加到0.61,横向应变均值由0.099 1×10-2增加到0.129 6×10-2,增幅30.78%,损伤量从0.61增加到1,横向应变均值由0.129 6×10-2增加到0.522 5×10-2,增幅303.16%。
对不同损伤量与水泥石试件横向应变关系进行拟合,可得
![]()
(11)
式中,ε2为后期水泥石试件横向应变,10-2。
相关性系数R2=0.999 2,表明采用指数增加函数式可以较好表征试件不同损伤量与试件横向应变的关系。
整体上,横向应变的变化更多反映压密后新裂隙萌生及扩展,且损伤试件内部随损伤量增加已产生不同程度裂隙衍化。
4.2 早期损伤与后期泊松比、弹性模量关系
从图18可知,随早期水泥石试件损伤量增大,后期水泥石试件的泊松比呈增加趋势,说明损伤水泥石性质已发生改变。损伤量从0.41增加到0.48,水泥石试件均值泊松比从0.106 6增加到0.113 6,增幅为6.57%,损伤量从0.48增加到0.61,水泥石试件均值泊松比从0.113 6增加到0.119 9,增幅为5.55%。
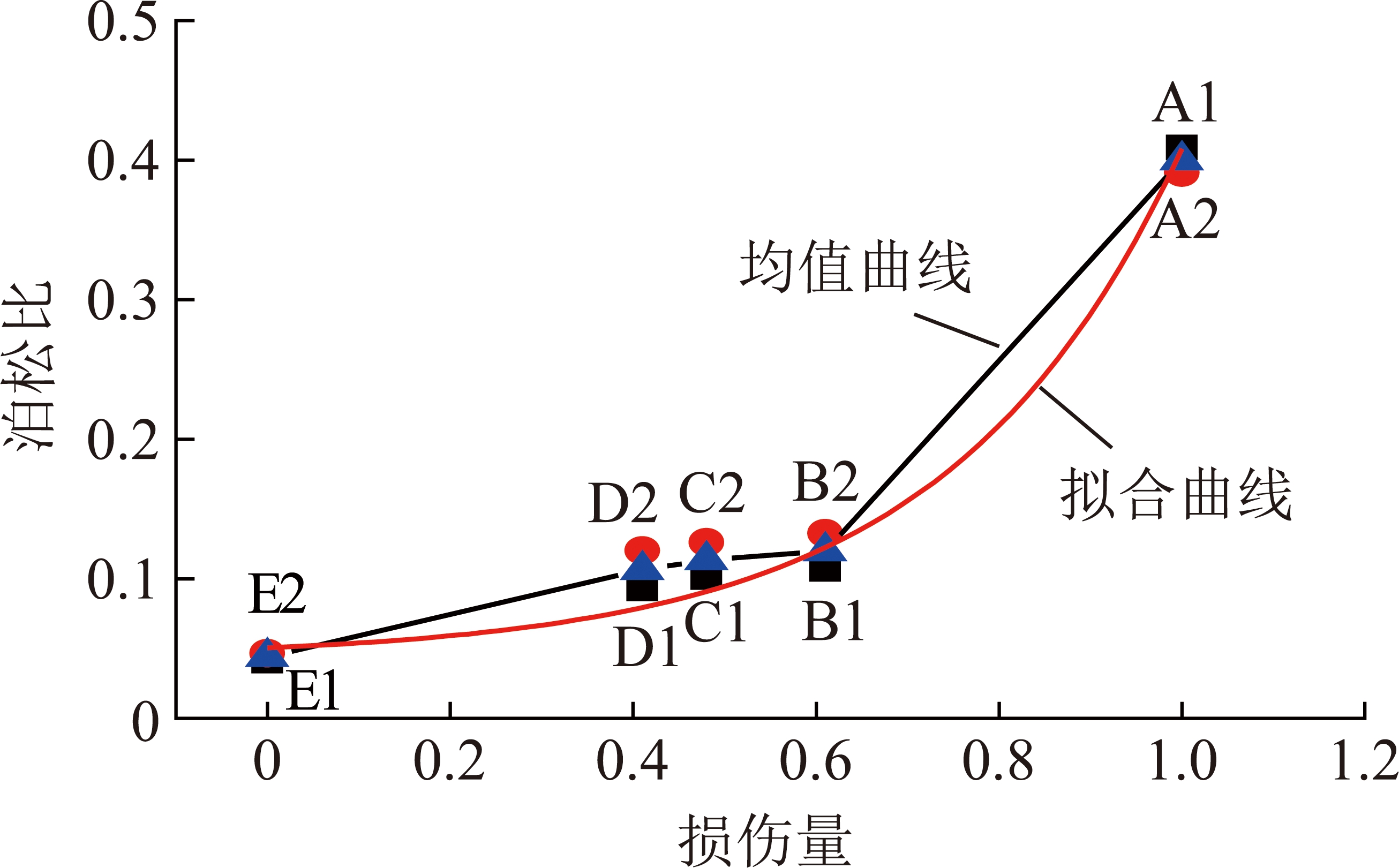
图18 损伤水泥石试件泊松比
Fig.18 Poisson’s ratio of damage cement specimens
对不同损伤量与试件泊松比关系进行拟合得
![]()
(12)
式中,μ为后期水泥石试件泊松比。
相关性系数为R2=0.993 0,指数增加函数式可以较好地表征试件不同损伤量与试件泊松比的关系。
损伤量大于0.48后,水泥石泊松比增幅有轻微放缓,表明水泥石损伤后的空隙压缩与二次裂隙扩展的开始,此时,早期水泥石损伤弱化了后期承载力学行为。
对于水泥石试件早期损伤量与后期弹性模量关系,随着早期损伤量的增加(0.41~1.00),后期水泥石弹性模量(图19)呈衰减趋势,从7.930 8,7.068 4,6.561 6 GPa衰减至4.184 9 GPa,即试件抵抗变形的能力变弱;且从0.41~0.48衰减幅度为10.87%,0.48~0.61衰减幅度为7.17%。
对不同损伤量与弹性模量关系进行拟合可得
E=6.297 9+6.168 4D-8.270 5D2
(13)
相关性系数为R2=0.958 5,二次多项式函数式可以表征试件不同损伤量与试件弹性模量关系。
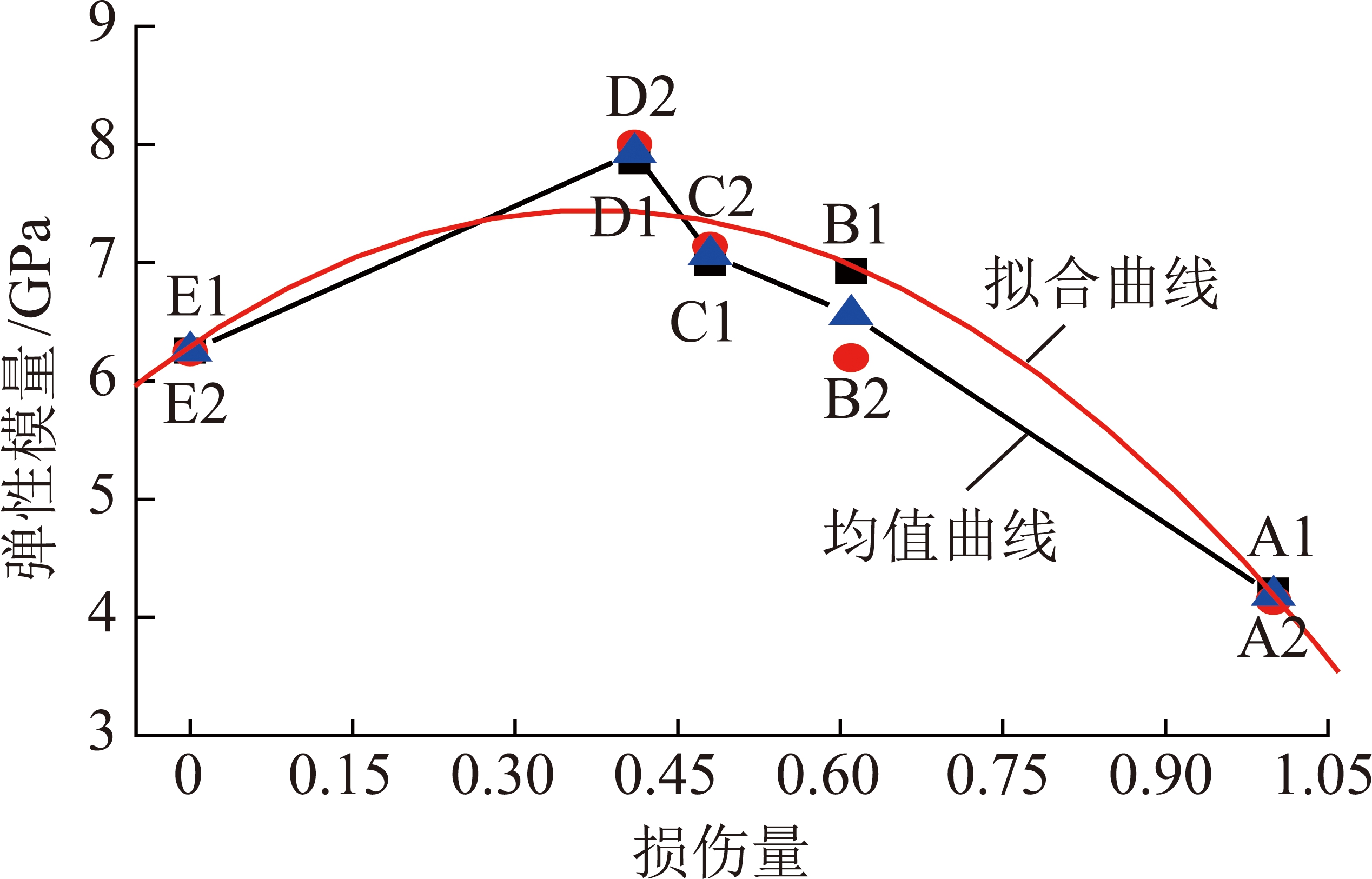
图19 损伤水泥石试件弹性模量
Fig.19 Elastic modulus of damage cement specimen
整体上看,随着水泥石试件早期损伤量的增加,水泥石试件弹性模量表现为先增加后减小的趋势,主要是因为较小程度的损伤提高了水泥石后期强度,而较大程度的损伤则会减小后期水泥石试件的强度,小于损伤阈值(0.48)的扰动损伤可以提高后期水泥石试件的稳定性。
4.3 水泥石试件破坏形态分析
4.3.1 破坏形态分析
由图20,21可观察到水泥石在不同损伤程度(0.41~0.61)下再进行单轴压缩试验产生的破坏形态要明显比无损组(E组)试件表现更加破碎。

图20 损伤水泥石破坏形态
Fig.20 Failure modes of damaged cement specimens
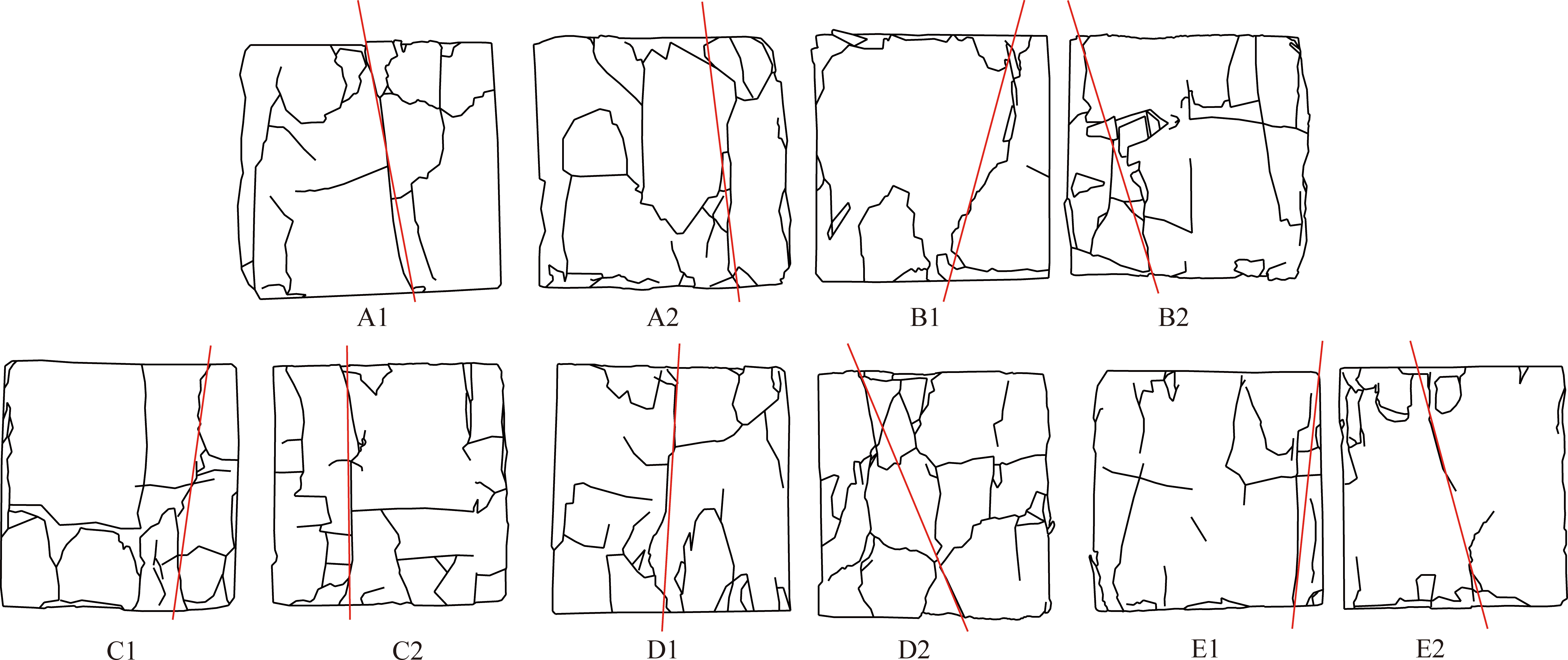
图21 损伤水泥石素描
Fig.21 Sketches of damage cement specimens
可以看出,损伤程度较大的水泥石破坏主控面明显,由单侧破坏导致试件整体丧失承载能力;而损伤程度较小的试件在破坏形态上表现较为复杂,存在纵横交错的裂隙使得试件划分为几个区域,由块体间失衡导致试件整体丧失承载能力。
4.3.2 失稳模式分类
依据损伤水泥石破坏形态(早期损伤试验A组与后期承载试验E组可归类为常规无损伤试验),将水泥石试件失稳分为2种模式。
(1)累贯穿失稳模式。水泥石试件在荷载作用下经过内部压密后,新的裂隙不断产生并积累,在此基础上贯穿后形成主控裂隙面,造成试件的整体失稳(图22(a)),适用于常规无损伤试验及高损伤的水泥石试件失稳。
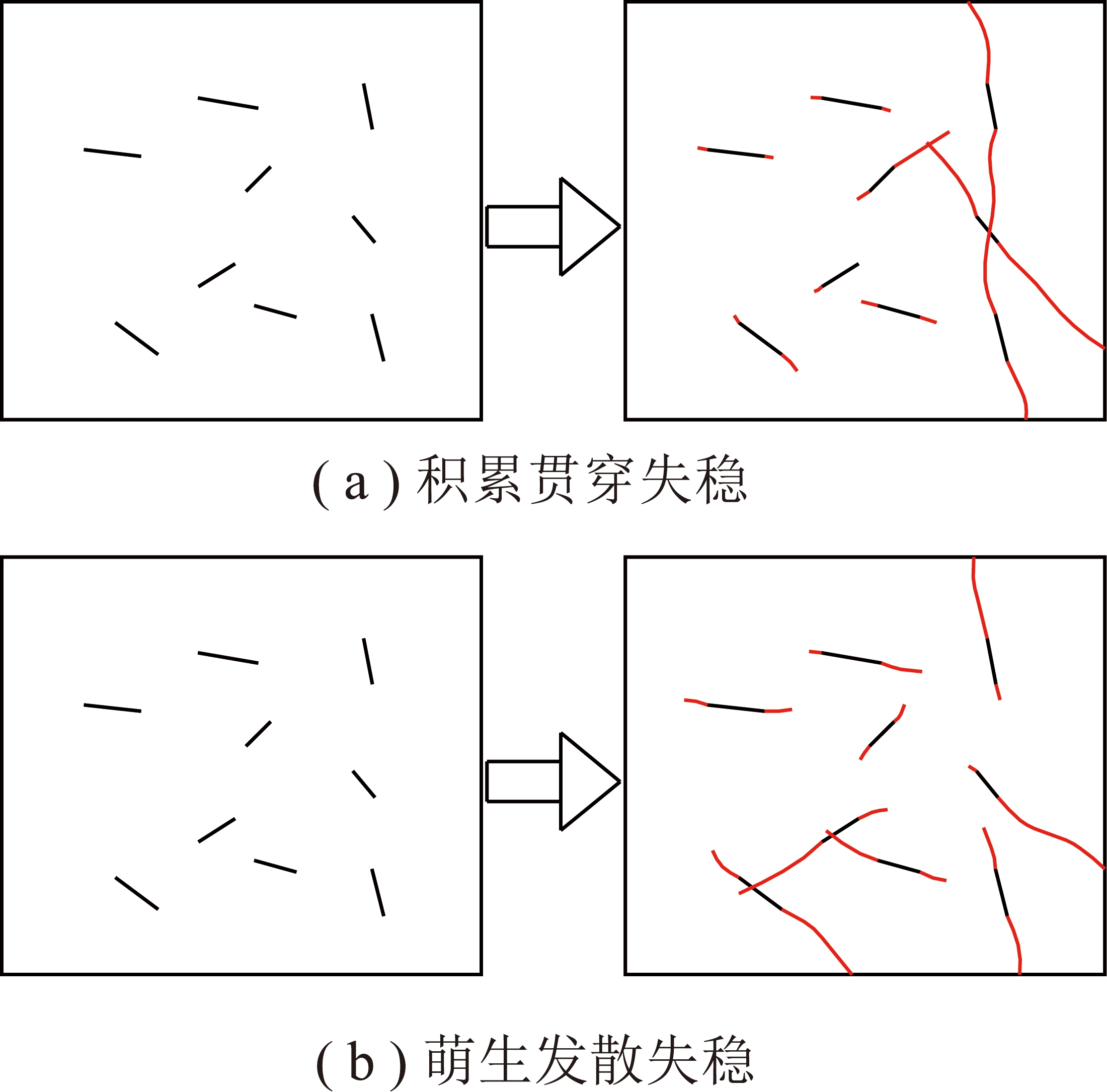
图22 水泥石试件失稳模式
Fig.22 Cement specimen instability modes
(2)萌生发散失稳模式。早期水泥石试件在不同终值荷载作用下内部结构受到损伤,使得试件内部出现许多新的裂隙,甚至出现不同程度贯通,后期再次受载时裂隙处出现应力集中,不再继续积累而沿裂缝处各自分散破坏,各部分结构面失去铰接而产生失稳(图22(b)),适用于受损伤程度较小的水泥石试件破坏失稳。
5 结 论
(1)确定了早期水泥石试件全应力-应变曲线条件下的损伤量求解方程,损伤曲线分为压密损伤、损伤累积与损伤爆发3个阶段。
(2)随着水泥石试件应力比增加(75%~100%),试件轴向应变、横向应变、泊松比与损伤量呈增加趋势,且横向应变增幅大于轴向应变,而弹性模量表现为衰减趋势。
(3)早期水泥石试件的80%应力比(损伤量为0.48)为损伤阈值,此值前后的早期损伤试件二次承载时分别表现为强度增强与强度衰减。
(4)随着水泥石试件早期损伤量增加,水泥石试件后期抗压强度、弹性模量呈先增加后减小趋势,轴向应变、横向应变与泊松比整体呈增加趋势。
(5)水泥石试件失稳模式分为积累贯穿失稳及萌生发散失稳,高损伤试件由单侧破坏导致试件失稳,低损伤试件由块体间失衡导致试件失稳。
[1] KANG Hongpu.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[2] 赵光明,张小波,王超,等.软弱破碎巷道围岩深浅承载结构力学分析及数值模拟[J].煤炭学报,2016,41(7):1632-1642.
ZHAO Guangming,ZHANG Xiaobo,WANG Chao,et al.Mechanical analysis and numerical simulation for deep and shallow bearing structures of soft and broken roadway surrounding rock[J].Journal of China Coal Society,2016,41(7):1632-1642.
[3] 张智慧,潘一山.深部巷道破坏分区破裂规律三维相似材料实验[J].煤炭学报,2015,40(12):2780-2786.
ZHANG Zhihui,PAN Yishan.Three-dimensional similar material experimental study on zonal disintegration of deep tunnel failure[J].Journal of China Coal Society,2015,40(12):2780-2786.
[4] 左建平,孙运江,王金涛,等.充分采动覆岩“类双曲线”破坏移动机理及模拟分析[J].采矿与安全工程学报,2018,35(1):71-77.
ZUO Jianping,SUN Yunjiang,WANG Jintao,et al.Mechanical and numerical analysis of “analogous hyperbola” movement of overlying strata after full mining extraction[J].Journal of Mining & Safety Engineering,2018,35(1):71-77.
[5] PETERSEN Derek,LIN Zhibin,ZHAO Jian.Shear behavior of single cast-in anchors in plastic hinge zones[J].International Journal of Concrete Structures and Materials,2018,12(1):56-68.
[6] SUN Lihui,WU Haoyuan,YANG Bensheng,et al.Support failure of a high-stress soft-rock roadway in deep coal mine and the equalized yielding support technology:A case study[J].International Journal of Coal Science & Technology,2015,2(4):279-286.
[7] ZHANG Zhongya,JIN Xiaoguang,LUO Wei.Mechanical responses of shotcrete specimens in direct shear tests[J].Construction and Building Materials,2018,188:305-313.
[8] WANG Jiabin,NIU Ditao,WANG Yan,et al.Durability performance of brine-exposed shotcrete in salt lake environment[J].Construction and Building Materials,2018,188:520-536.
[9] FANG Shulin,ZHANG Jian.In-situ measure to internal stress of shotcrete layer in soft-rock roadway[J].International Journal of Coal Science & Technology,2014,1(3):321-328.
[10] YAO Wei,XIA Kaiwen,LIU Hungwei.Influence of heating on the dynamic tensile strength of two mortars:Experiments and models[J].International Journal of Impact Engineering,2018,122:407-418.
[11] 陈昌宏,张倩,朱彦飞,等.外加剂对水泥石力学性能的影响[J].油田化学,2017,34(3):428-432.
CHEN Changhong,ZHANG Qian,ZHU Yanfei,et al.Effect of admixtures on mechanical properties of cement[J].Oilfield Chemistry,2017,34(3):428-432.
[12] 徐礼华,李长宁,李彪,等.循环受压状态下钢纤维混凝土一维弹塑性损伤本构模型研究[J].土木工程学报,2018,51(11):77-87.
XU Lihua,LI Changning,LI Biao,et al.Investigation on 1d elasto-plastic constitutive model of steel fiber reinforced concrete under uniaxial cyclic compression[J].China Civil Engineering Journal,2018,51(11):77-87.
[13] MURTHY A R,KARIHALOO B L,RANI P V,et al.Fatigue behaviour of damaged RC beams strengthened with ultra-high performance fibre reinforced concrete[J].International Journal of Fatigue,2018,116:659-668.
[14] 刘娟红,周昱程,纪洪广.单轴加卸载作用下井壁混凝土能量演化机理[J].煤炭学报,2018,43(12):3364-3370.
LIU Juanhong,ZHOU Yucheng,JI Hongguang.Energy evolution mechanism of shaft wall concrete under uniaxial loading and unloading compression[J].Journal of China Coal Society,2018,43(12):3364-3370.
[15] 褚怀保,杨小林,叶红宇,等.新浇混凝土爆破振动损伤累积规律模拟试验研究[J].煤炭学报,2018,43(9):2469-2475.
CHU Huaibao,YANG Xiaolin,YE Hongyu,et al.Simulation experimental research on damage accumulation law of new concrete under multiple blasting vibration loads[J].Journal of China Coal Society,2018,43(9):2469-2475.
[16] HU F,WU H,FANG Q,et al.Impact resistance of concrete targets pre-damaged by explosively formed projectile (EFP) against rigid projectile[J].International Journal of Impact Engineering,2018,122:251-264.
[17] LIU Ruyue,YANG Yong,ZHOU Xianwei.Experimental study on fatigue performance of composite beam with steel-plate-concrete composite decks[J].Construction and Building Materials,2018,188:833-849.
[18] 李晓琴,陈保淇,杜茜,等.混凝土SHPB动态抗压试验数值模拟研究[J].机械强度,2018,40(4):901-907.
LI Xiaoqin,CHEN Baoqi,DU Xi,et al.Numerical simulation of shpb dynamic compression test of concrete[J].Journal of Mechanical Strength,2018,40(4):901-907.
[19] BRYANT E C,SUN Waiching.A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics[J].Computer Methods in Applied Mechanics and Engineering,2018,342:561-584.
[20] 李康,刘娟红,卞立波.复合胶凝材料井壁高强混凝土的性能与水化机理[J].煤炭学报,2015,40(S2):353-358.
LI Kang,LIU Juanhong,BIAN Libo.Properties and hydration mechanism of composite binder used in high strength shaft concrete[J].Journal of China Coal Society,2015,40(S2):353-358.
[21] 束伟,钱文勋,陈迅捷.高温-水冷循环作用下的水泥石劣化分析[J].硅酸盐通报,2018,37(1):80-85.
SHU Wei,QIAN Wenxun,CHEN Xunjie.Deterioration analysis of cement paste under heat-water circulation[J].Journal of the Chinese Ceramic Society,2018,37(1):80-85.
[22] 魏建军,邢姣秀,付智.行车荷载引起桥梁振动对修复混凝土性能影响[J].东南大学学报(自然科学版),2010,40(5):1057-1060.
WEI Jianjun,XING Jiaoxiu,FU Zhi.Effect of traffic load induced bridge vibrations on concrete tensile properties[J].Journal of Southeast University(Natural Science Edition),2010,40(5):1057-1060.
[23] 蒋正武,任强,袁政成.车桥耦合振动对混凝土早期性能的影响及其损伤机理[J].建筑材料学报,2015,18(3):471-476.
JIANG Zhengwu,REN qiang,YUAN Zhengcheng.Effects of vehicle-bridge coupled vibration on early-age properties of concrete and its damage mechanism[J].Journal of Building Materials,2015,18(3):471-476.
