世界上有很多国家面临地质灾害频发的问题[1-2]，人民生命财产安全和社会发展受到了严重威胁[3-4]。随着量测技术的发展和仪器精度的提高，安全监测在边坡工程中的应用越来越广泛[5-6]，弥补了极限平衡法、数值模拟等手段在边坡动态稳定性分析方面的不足。充分利用其获得的动态监测数据对失稳边坡进行预警成为了岩土工程领域的研究热点[7-8]。
围绕该难题，SAITO M[9]首先基于对边坡破坏现场实测记录的检验，提出了“斋藤模型”，为理解稳定蠕变与加速蠕变阶段的应变速率如何影响滑坡发生的位置、时间和速度等问题提供了理论框架;KAWAMURA[10]采用最小平方法及P阶差分方程的滞后算子分解形式求解Saito公式，使得斋藤模型精度得到较大提高。在此基础上，近年来越来越多的滑坡预警方法被提出，如统计方法[11-13]、灰色理论[14-15]、边坡位移预测模型[16-18]等。这些方法大多需要通过阐明滑坡与地质地貌条件、水文环境等静态特征因素间的潜在关系来分析滑坡的演化状态。然而，这些模型也有明显的缺点:使用范围有限，对原始监测数据质量要求高。露天矿由于受到监测设备成本高、动态开采以及监测设备布设困难等因素制约，限制了通过多元数据观测滑坡体在各种外部影响因素作用下的特征响应。所以要根据现有露天矿普遍采用的GPS位移监测设备，根据获取到的表面位移监测数据进行滑坡预警模型的建立与分析。边坡位移监测数据通常为二元属性变量，即安全与不安全。系统聚类分析方法可以从数据中提取状态模式，将数据进一步简化，使数据不受单位量级等其他噪声的干扰[19-23]。在露天矿滑坡预警中，系统聚类方法可以对采集到的监测数据进行状态表达，为进一步的数据分析提供基础。随着信息论和数值计算方法的不断发展，马尔科夫链的出现为滑坡预警提供了一种可能性，它能够在掌握有限数据的状况下，利用其无后效性预测优势[24-26]，来描述滑坡演化与其运动规律的随机性态。系统聚类分析与马尔科夫预测理论虽然分别在信息科学与工程科学中广泛应用，但是二者耦合模型在滑坡预警的应用研究目前还较少。
预警指标的选择是预警过程中的重要一步，以往的研究多将相对保守、经验成分居多滑坡变形类判据作为预警基础:如李聪等[27]选择变形速率为指标，来探究滑坡不同演化阶段的演化规律;许强等[28]利用改进切线角模型对斜坡加速度变形阶段的状态进行了进一步的细分。但是这些模型的预警精度和预警区域的准确性仍然有待提高。针对这一问题，王东等[29]认为加速度应该成为“预测滑坡发生故障的基础”，建议将加速度大于0作为滑坡预警准则，并从统计学的角度对该准则进行了描述，提出了边坡临滑时刻(DYMIS)的预警模型评价方法，克服了以往采用速率阈值预警不具有普适性的不足。但该种方法一般在滑坡启动后方能做出判断，因此存在一定的预警滞后问题。为此，笔者基于马尔科夫链预测理论与系统聚类的基本思想，从滑坡判据的合理选取与描述入手，兼顾预警的及时性、抗干扰性及可信度，探索一种新的滑坡预警方法，为准确、及时实施滑坡预警提供科学手段。
1 系统聚类-加权马尔科夫链耦合滑坡预警方法研究
在随机过程中，马尔科夫性质是指一个随机游动模型在给定现在状态(present state)及所有过去状态(state space)集合的情况下，其未来状态的条件概率(Conditional Probability，CP)分布仅受当前状态控制，其实质是利用初始概率(Initial Probability，IP)和不同状态的关系转换概率(Transition Probability，TP)来表示状态的过渡进程，在预测领域应用极为广泛[30]。不难想象，滑坡的发生必然要经历位移逐渐增加的过程，在该过程中，在离散时间下任一时刻的位移速度是随机的，且下一时刻的位移速度不受当前时刻的影响，为典型的马尔科夫链(图1)。另一方面，边坡的稳定性状态可严格地划分为两种，即“稳定”与“不稳定”，若能找到恰当的状态判断标准，即可利用马尔科夫链理论对边坡的状态进行预测，再结合该标准，做出是否应该进行滑坡预警的判断。
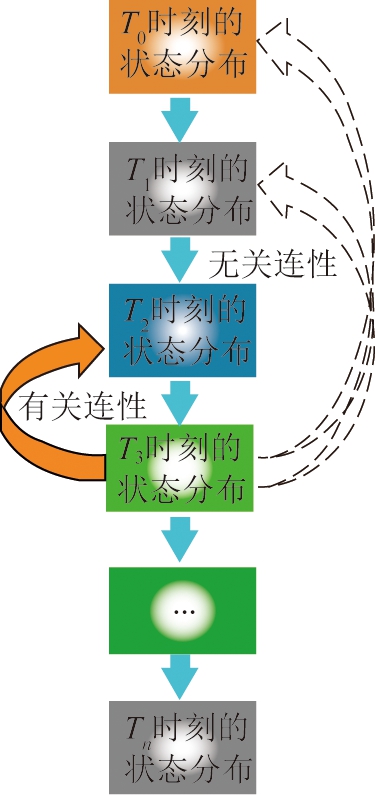
图1 系统聚类马尔科夫示意
Fig.1 Markov diagram of hierarchical clustering
系统聚类是最基本和最常见的一种状态划分方法;该方法将分类对象中两个最相似的组合聚合成一对集群,并构造一个新的层次分类结构，便能自然地、客观地得到一张完整的分类系统图[31]。因此，笔者将马尔科夫链理论与系统聚类方法相结合，试图在选取合理滑坡判据的基础上，应用马尔科夫链理论对其进行描述，然后借助系统聚类方法对边坡状态进行划分，构建一种新的滑坡预警模型，为有效实施滑坡预警奠定理论基础。
1.1 系统聚类加权马尔科夫(MCL)的基本原理与步骤
依据马尔科夫链理论，如果把训练数据集中随时间演变的位移速度V看作是一组随机变量{V(t),t∈T}(T为时间)，并根据离散时间下速度随机变量V(t)监测值，建立合理的状态分类标准，并得到原始速率时间序列下的状态序列;则这个状态序列记录了位移速度变化的时间信息，由此构造出了离散时间序列下不同速度状态频率所占空间比，由此得出的状态转移概率矩阵(State Transition Probability，STP)也就包含了边坡稳定性状态随时间变化的统计规律性[32]。因此，在位移速度数据的动态更新中，马尔科夫链可以通过对动态系统中时变参数的动态运算，不断对未来位移速度的状态做出同时包含统计规律性和时间信息的预测。在应用马尔科夫链理论进行状态预测时，由于单一初始状态具有较大的偶然性，步长为1的状态转移概率矩阵也不能充分刻画状态的内部转移结构。因此，本文采用系统聚类加权马尔科夫耦合模型对边坡状态进行预测，该方法引入了不同步长的STP对预测结果的影响，充分将原始数据中所隐藏的预测信息抽取出来。
具体预测步骤如下:① 收集某监测点的位移速度数据序列，选择样本容量n。② 将数量为n的初始样本速度数据序列划分为n等份。③ 采用重心法(Centre gravity method)计算初始节点每个速度数据之间的距离，将距离最小的两组数据合并为一类。④ 重复步骤②，绘制位移速度状态系统聚类树。根据统计学中的定序尺度，将位移速度的状态描述为二元属性，即“正常”和“异常”两种状态。基于布尔运算分别用数字“1”和“2”表示这两种状态。⑤ I为定义向量，根据速度数据的初始状态分布序列，统计出包含每个离散时间戳下步长为k(k=1,2,…,r)的状态转移频数矩阵[33]。由速度数据状态转移频数矩阵计算出速度数据的状态转移概率矩阵。假定速度状态数据序列中的每个数据xi的概率只取决于前面N-1个数据有关，由此确定模型的IPV。根据N元模型时马尔科夫预测所得的xn+1的状态分布向量，得出N取不同值时
的组成矩阵B。⑥ 以分步长的加权值作为子序列，以各步长加权值构成m阶权值矩阵w=(w1,w2,…,wm)为主序列。求模型自相关系数(ACF)，并据此由m阶加权向量求二者的相关系数就得到了原时间序列的ACF。⑦ 得到m阶加权马尔科夫预测的未来状态的分布概率向量C，C中最大元素所在列对应的状态即加权马尔科夫链预测的xn+1的最可能状态。⑧ 以预警准则检验当日、前日位移速度状态及次日位移速度预测状态，判定是否应进行滑坡预警。⑨ 更新数据，删除样本中时间最靠前的数据，保持样本容量为n不变，返回步骤②继续执行直至不再获取新数据。
显然，在马尔科夫链预测理论的预警模型中，对所采集到的位移速度状态的真实信息和预测信息进行描述，基于这两种信息状态反馈可确定边坡稳定性状况表现。因此，应用加权马尔可夫链理论进行滑坡预警判断的详细步骤及流程如图2所示。
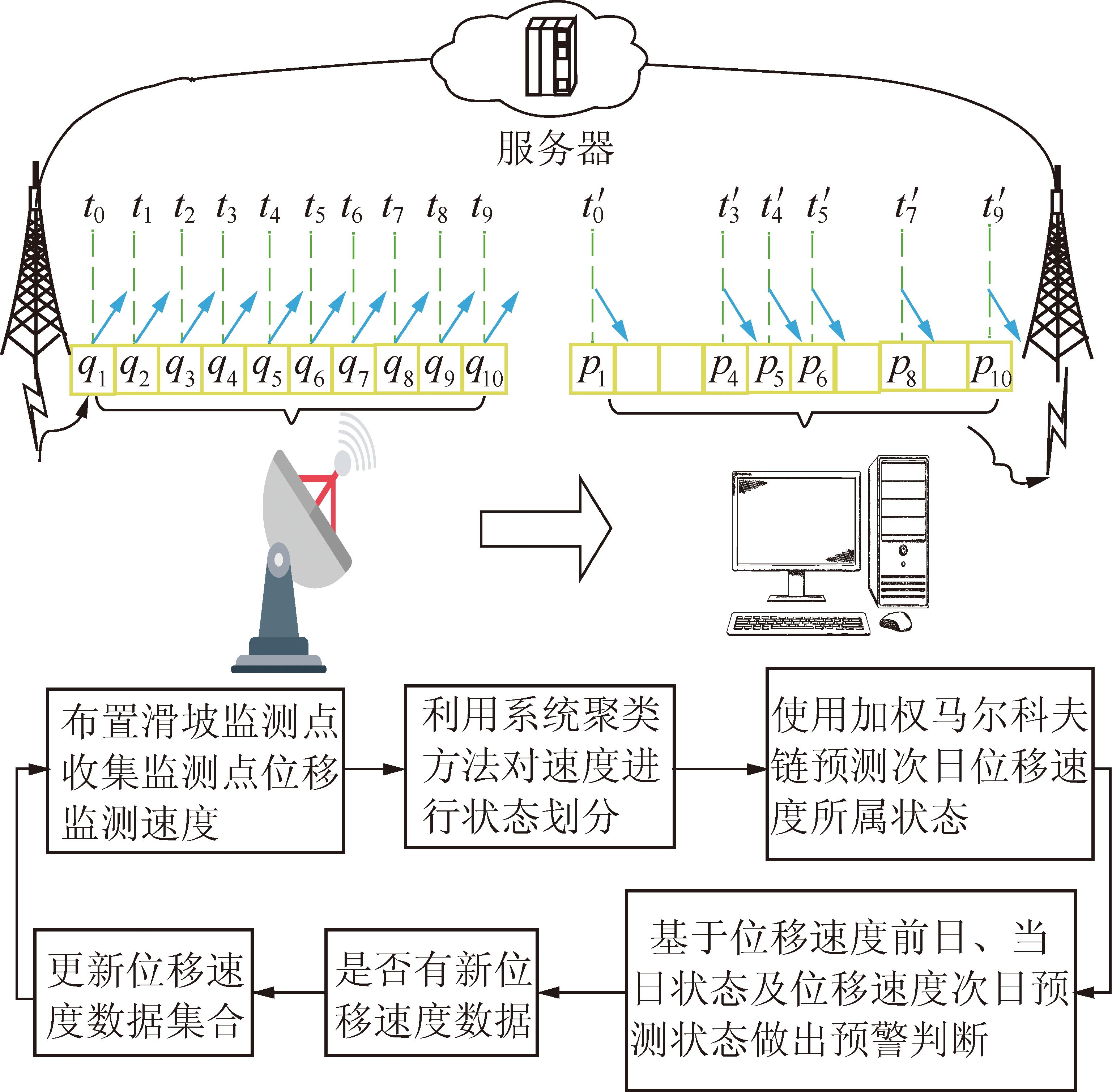
图2 滑坡预警判断流程
Fig.2 Judgment and flow chart of landslide early warning
图2中的计算方法中所涉及到的公式包括:
速度数据状态转移频数矩阵(STFM)[33]
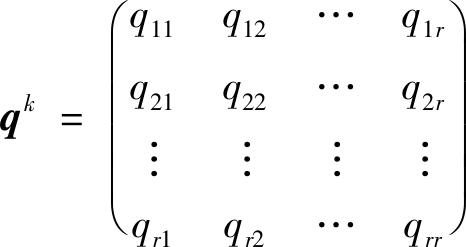
(1)
速度数据状态转移概率矩阵(STPM):
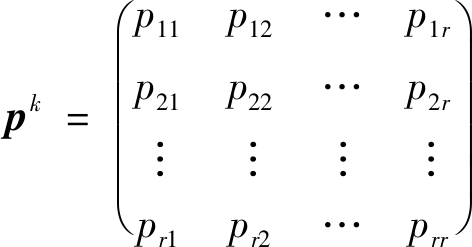
(2)
式中，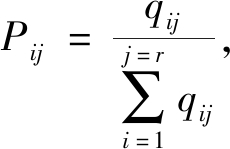
对于
的值可以由大数定理[34]近似认为和测试数据的相对频度相等。
初始概率向量(IPV):
(3)
式中，
状态分布向量(SDV):
(4)
N取不同值时的各
的组成矩阵
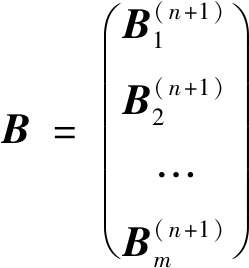
原时间序列加权向量的协方差与标准差关系表达式为
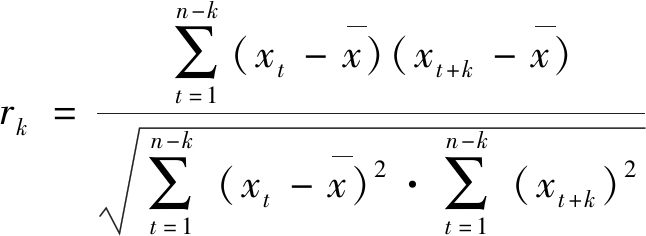
(5)
不同步长的m阶加权矩阵w=(w1,w2,…,wm)
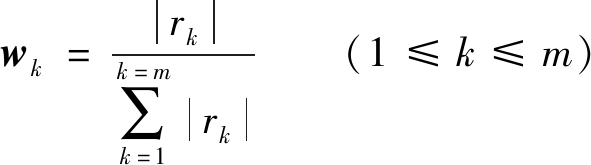
(6)
马尔科夫状态预测结果为
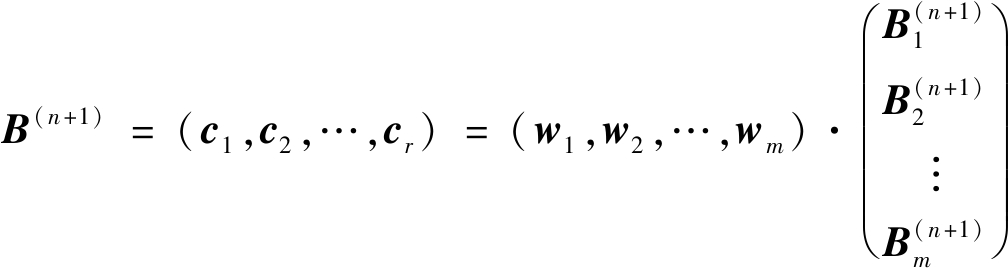
(7)
1.2 基于马尔科夫链的滑坡判据
按照滑坡三阶段理论[35-36]，加速度a>0即预示着滑坡将要发生，该判据能够克服广泛应用的变形速率阈值判据不具有普适性的缺点。但由于工程环境中各类特定因素的影响，获得的监测位移速度数据存在许多噪声，从而无法对位移速度历时曲线进行很好的拟合，也就不能对边坡进入加速变形阶段的破坏时间进行准确评估[37]。因此，如何基于马尔科夫链预测理论的基本思想，合理描述这一滑坡判据是实现较为精准、及时滑坡预警的重要前提。
加速度a>0的实质是位移速度值的增大，而马尔科夫链理论预测的是状态的改变。显然，对于一定容量的位移速度数据，可采用系统聚类方法将其划分为两类，较大的一类界定为相对危险的“异常”状态，较小的一类界定为相对安全的“正常”状态。通常，在边坡加速变形阶段，位移速度会连续出现较大值，马尔科夫链理论也必将连续给出状态“异常”的预测结果。另一方面，为避免位移矢量出现负值或系统粗差而造成的状态划分偏差，应将动态样本的位移速度均值和标准差均增大作为滑坡预警的限制条件。因此，可将加速度a>0的判定条件描述为:监测获得的前日与当日位移速度状态为“异常”，预测获得的次日位移速度状态为“异常”，动态样本的位移速度均值和标准差持续增大。
2 滑坡预警有效性评判标准的提出
假设各监测点监测周期为1 d，需提前预警的天数为R。为保证滑坡预警的及时、可靠，同时在滑坡演化各阶段的状态预测中保持较高的可信度，笔者按照重要程度，顺序提出以下3个滑坡预警的有效性评价标准。
(1)假设在滑坡前R天之内给出的预警信号次数为R*，则预警敏感度I=R*/R。I越大，预警滞后效应越能得到校正;当I=1时，预警从时间上最为及时。
(2)假设在临滑R天之前做出的M次判断中，有M*次给出了预警信号，则预警正确率W=1-M*/M。W越大，预警可靠性越高;当W=1时，预警的可靠性最高。
(3)假设滑坡发生前对次日位移速度状态给出了Q次预测，其中Q*次与实际相符合，则预测共识率Y=Q*/Q。Y越大，预测的可信度越高;当Y=1时，预测状态与真实状态完全一致。
3 工程应用
3.1 工程地质概况
平庄西露天矿位于内蒙古自治区平庄市，露天矿顶帮最大高度逾300 m，走向长度约4 km，西临五家井工矿(图3)，受露天、地下联合开挖及断层、弱层等一系列因素影响，曾多次发生滑坡，严重威胁露天矿安全生产。因此，以50～200 m为间距，分别在不同台阶布置了数十个表面位移监测点，为了解滑坡的变形特征，以达到避免因突发性边坡失稳事故而造成人员伤亡的目的。
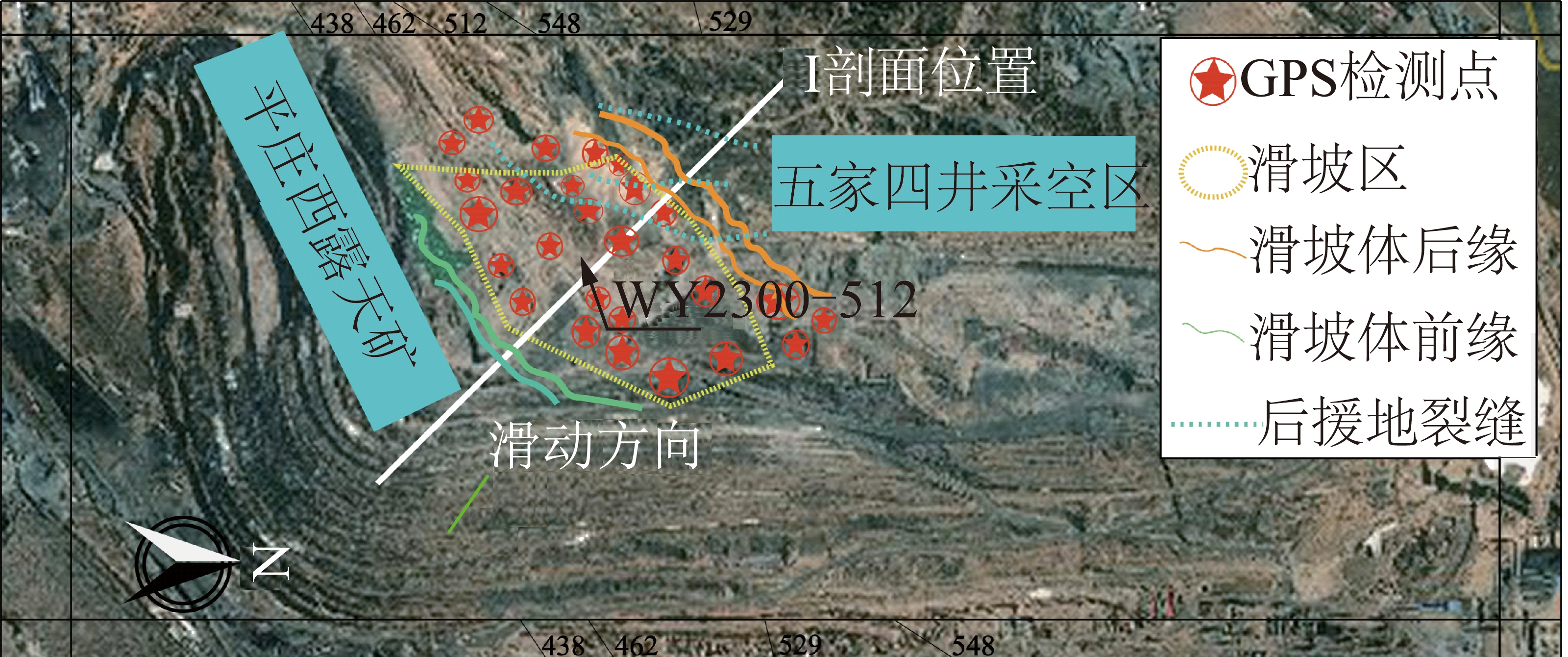
图3 平庄西露天矿遥感正射卫星图
Fig.3 Satellite image of Pingzhuang west open-pit mine
西露天矿顶帮主要由侏罗系砂泥岩互层组成，此种岩性特征导致顶帮在软弱夹层的泥化影响因素下于2013-04-17发生滑坡。滑坡的边界特征为:滑体整体向ES方向滑移，滑坡总体上呈扇形展布(图4);滑体前缘以舌形形状投入采场沟谷，向ES60°伸出约160 m;后缘以西露天矿与五家矿四井边界处为界;滑体高差近200 m、NS宽约700 m、EW向长约400 m、体积约3×106 m3，属大型岩石深层滑坡。发生滑坡时周边共布置了28个表面位移监测点组成系统监测网，其中滑坡区外布设了7个地表位移监测点。
图4 滑坡区全貌
Fig.4 General view of landslide area
采用3DMine采矿设计软件对工程地质平面图进行可视化建模，图5分别为滑坡前后工程地质平面图。以Ⅰ剖面图(图6)为例进行斜坡结构以及滑坡变形破坏模式分析。
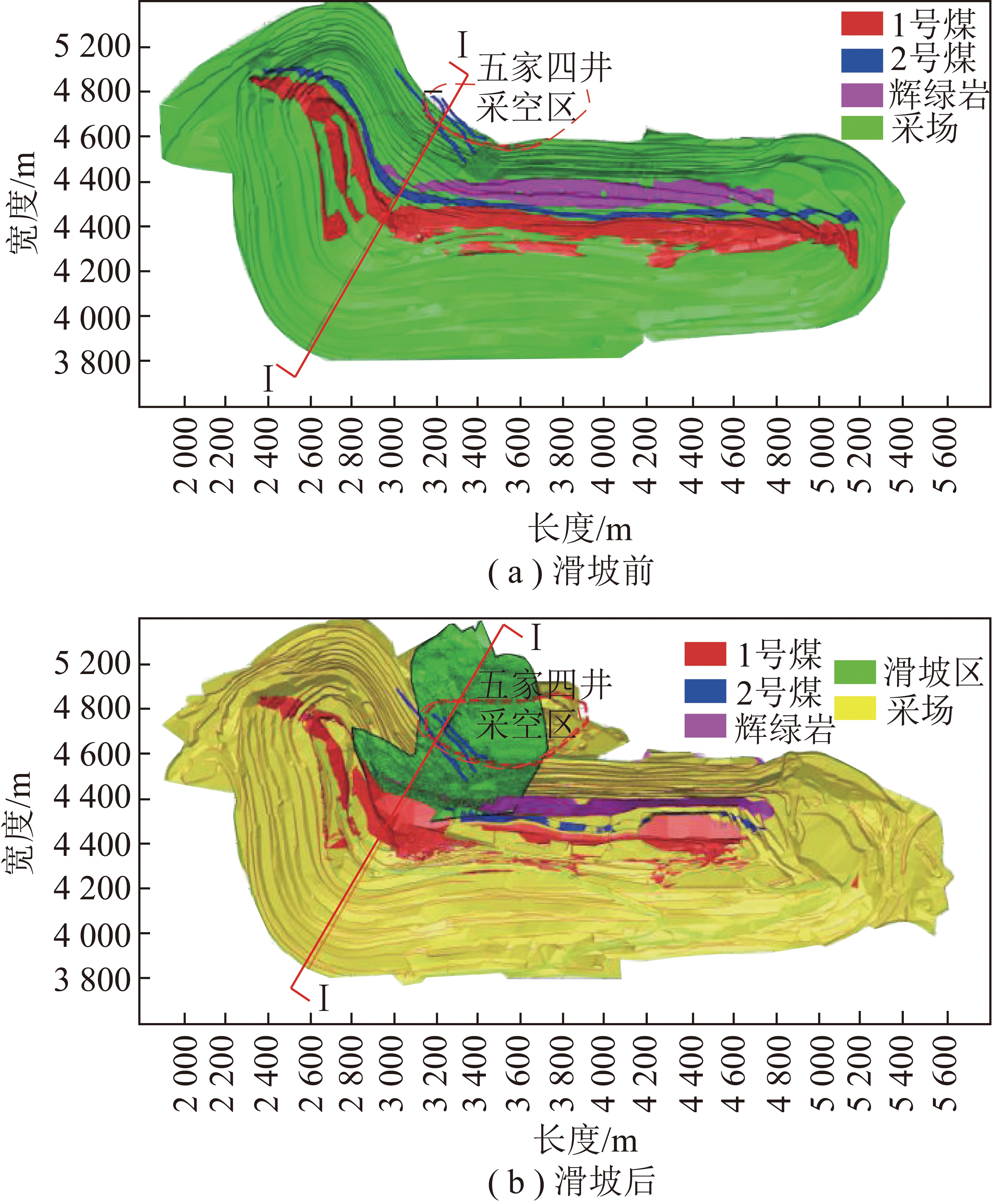
图5 “4·17”滑坡前后三维地质模型
Fig.5 3D geological model before and after “4·17” landslide
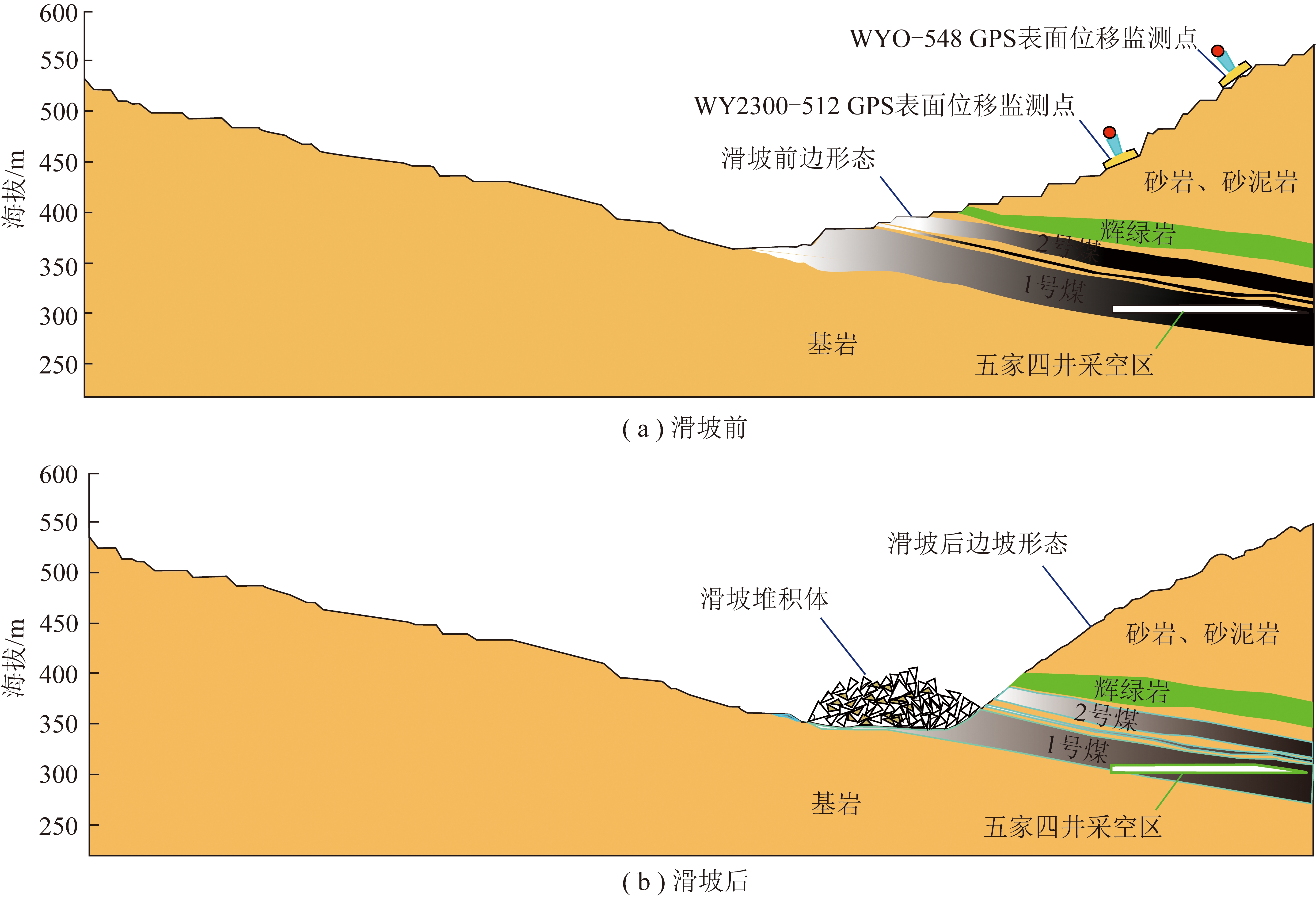
图6 “4·17”滑坡前后剖面
Fig.6 Profile map before and after “4·17” landslide
经过前期勘探，煤矿标高+320 m以上地层大多数已揭露。斜坡顶帮分布多以泥岩、砂岩混合为主，该层岩性抗剪能力差，边坡易沿该层发生切层-顺层滑动，早期滑坡多以此为滑动面。2号煤顶板以上，顶帮泥砂岩底板下属辉绿岩层组结构。该层组抵抗变形能力强，对顶帮岩体起到承载作用。1，2号煤层分布面积广泛、层位稳定，为本区主采煤层。临近的五家矿四井开采活动在+300～+350 m形成采空区，造成坡体岩层发生错动和弯曲变形，改变了边坡岩层完整性和降低了边坡稳定性。根据灾后勘察期间的观测记录结果显示，在滑坡区顶部边坡走向方向的地表新生成3条裂缝，均在滑体后缘附近，且为张裂缝。后缘地裂缝均是在滑坡后产生，因此不作为本次滑坡影响因素。
根据地形地貌、斜坡结构等特征分析可知:“4·17”滑坡变形破坏模式是前缘岩土体在上部压应力的作用下先形成临空面，产生滑移;继而向后缘发展。在临近滑坡区后缘五家四井地下开采活动和采场内采剥工程进行的共同影响下，边坡变形破坏速度加快，最终导致紧临前缘的岩土体在重力作用下发生垮塌。因此，“4·17”滑坡为典型的牵引式滑坡。
3.2 基于监测数据的滑坡演化过程分析
由于滑坡是一种复杂的多过程现象，滑坡演化过程的识别是滑坡预测预警的前提和基础。在滑坡的孕育和发展演化过程中，滑坡可分为初始变形阶段、等速变形阶段和加速变形阶段。同时，基于28个监测点速度数据的交叉汇编和分析，“4·17”滑坡不同部位变形的影响规律和程度在不同变形阶段存在差异。
通过分析在滑坡区及区域外监测网的监测数据(图7)可知:在滑坡变形初期，512测线WY2300-512监测点位移速度有变形启动趋势，其余监测点位移速度变化较为平稳。此阶段滑体位移虽有逐渐增大趋势，但是整个滑体仍处于恒速蠕变阶段。
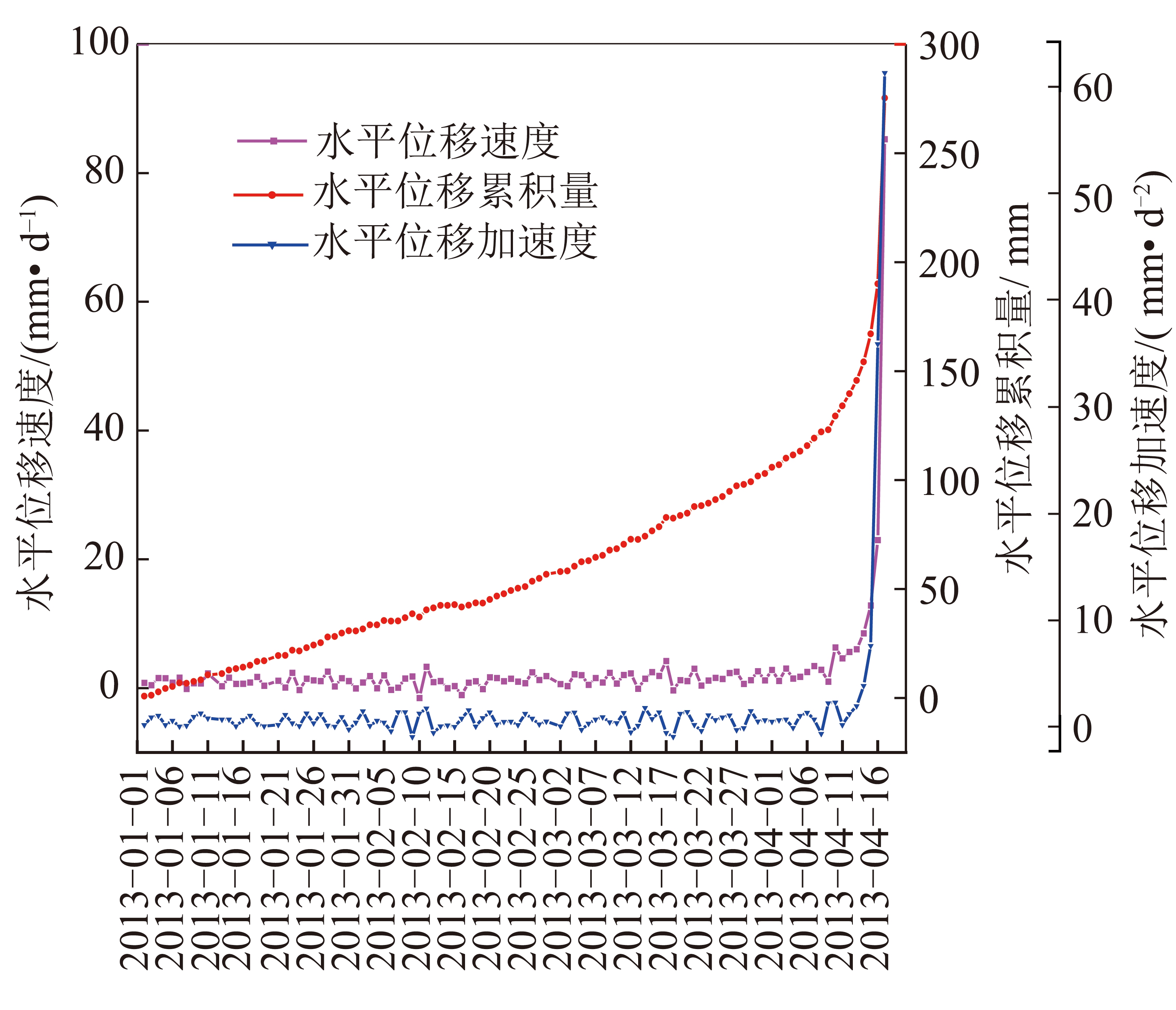
图7 监测点WY2300-512水平方向监测曲线
Fig.7 Curves of monitoring point WY2300-512 in horizontal direction
随着时间的延续，位于滑体后边界的548测线处位置稳定性较差，位移速度数据变化大幅度增加，地表的地裂缝加大，这可能是由于强烈的外界因素导致的(采坑加深，春季冰雪解冻和露天矿爆破震动)。但据现场勘探资料显示，此时滑体前缘部位并未出现大规模裂缝和宏观变形。
从2013-04-15开始，滑体加速蠕变阶段特征明显，系统监测网范围内各监测点位移速度数据时间序列呈跃阶状加速。直至4月17日，滑坡位移速率达到最大，发生滑坡。
3.3 一定样本容量下的边坡状态预测
3.3.1 边坡状态划分
为了检验所构建的预警工况能否满足开发需求，由于512测线上2300为初始变形点，所以采用TM30智能机器人，对标识的监测点从2013-01-01—04-17进行较为完整的监测数据采集，对此模型进行检验。25个监测数据作为样本容量，求得均值
标准差s=0.698。对长度为25的数据序列，由重心距离法求两两数据之间的绝对距离dij，形成25×25的距离矩阵。根据所求的距离进行归类，创建系统聚类树，如图8所示，完成聚类过程。由此聚类结果，并根据实际情况将位移速度大表示边坡安全性差，对应状态应为“异常”;所以，要使较大数据所在的类别为2，较小数据所在的类别为1，即把较大的异常于其他数据的数据状态界定为“异常”，依此标准，得到修正后的状态并将其列于表1中。
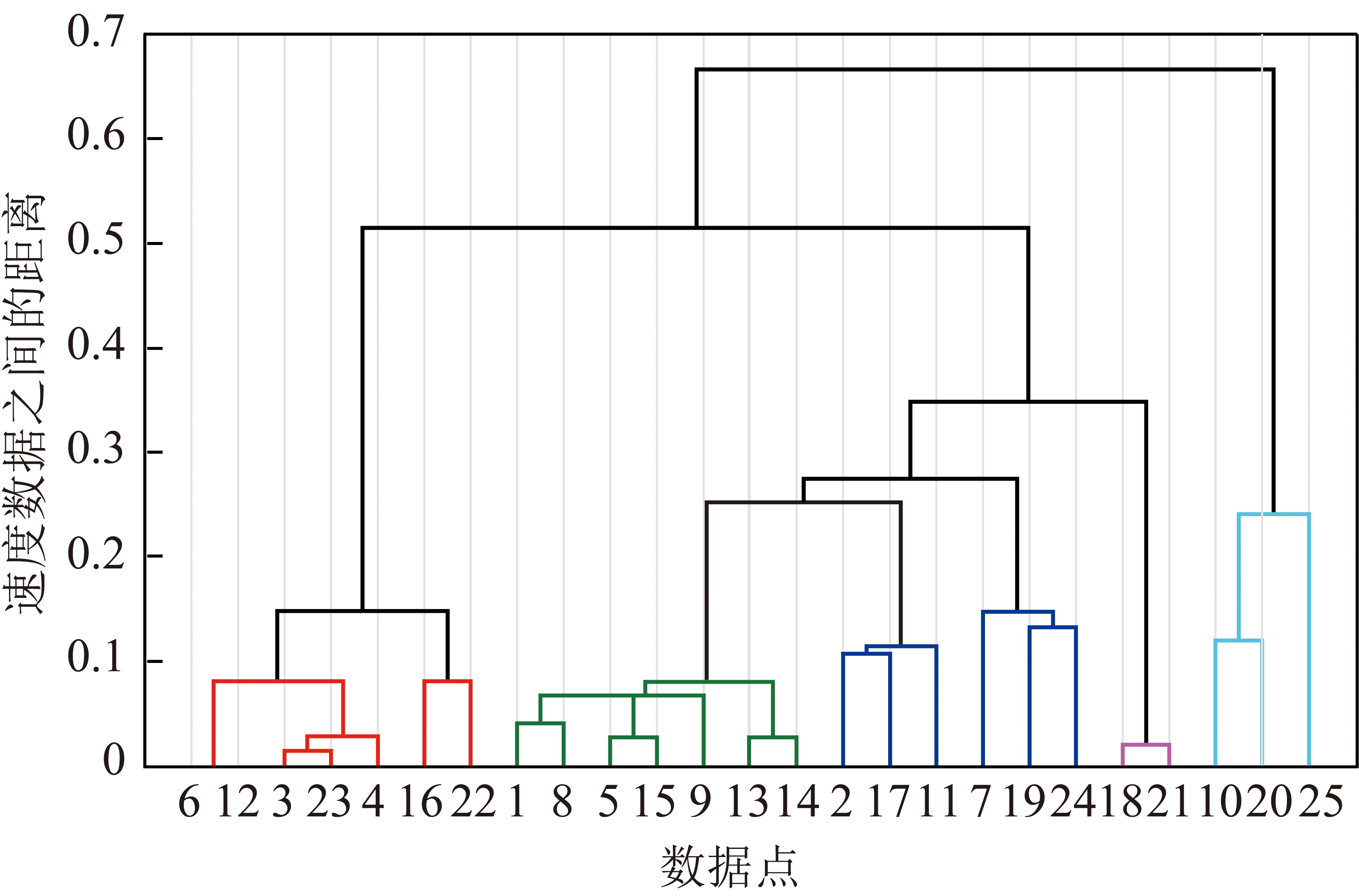
图8 谱系聚类
Fig.8 Hierarchical clustering figure
表1 WY2300-512监测点状态划分
Table 1 State division of WY2300-512 monitoring point
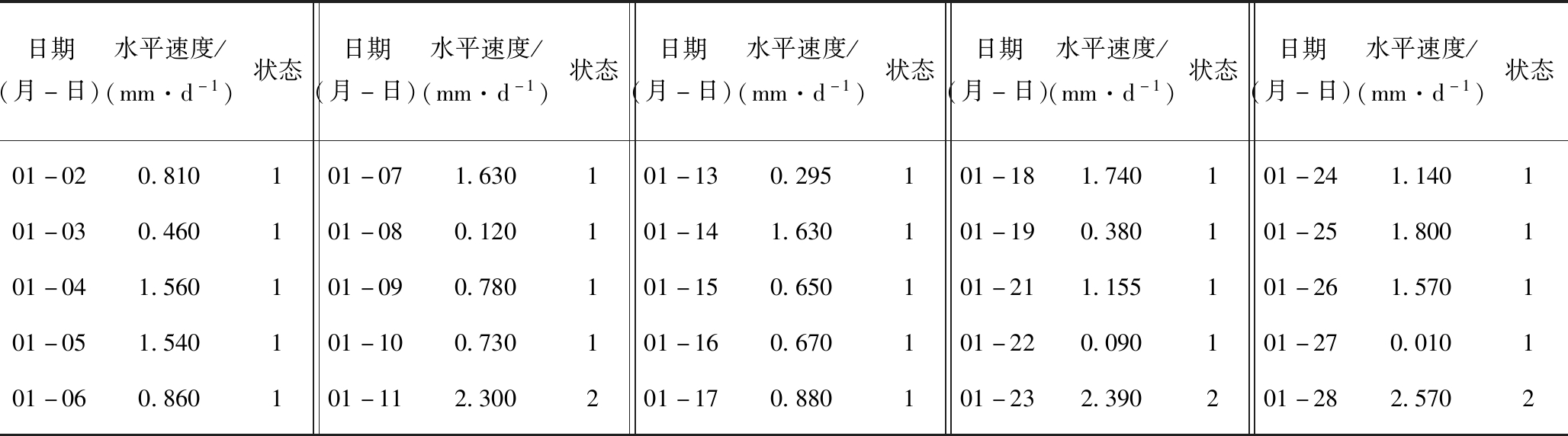
日期(月-日)水平速度/(mm·d-1)状态日期(月-日)水平速度/(mm·d-1)状态日期(月-日)水平速度/(mm·d-1)状态日期(月-日)水平速度/(mm·d-1)状态日期(月-日)水平速度/(mm·d-1)状态01-020.810101-071.630101-130.295101-181.740101-241.140101-030.460101-080.120101-141.630101-190.380101-251.800101-041.560101-090.780101-150.650101-211.155101-261.570101-051.540101-100.730101-160.670101-220.090101-270.010101-060.860101-112.300201-170.880101-232.390201-282.5702
3.3.2 加权马尔科夫链预测过程
统计可知，在上述所得状态空间序列中，据此统计可知，在上述所得状态空间序列中，据此可求得一元模型的STFM及STPM如下:
同理，得到二元、三元模型的STFM及STPM如下:
对于本实例选取的25个数据，第25个数据的状态为2，由式(4)求得一元模型的初始状态向量为
同理，第24，23，22，21个数据的状态为分别为1,1,1,1，对应1元模型的初始状态向量分别为:
根据式(5),(6)可求得各步长ACF和逐次转移的加权向量，各步长对应ACF分别为r1=-0.520 7，r2=-0.295 3，r3=-0.290 6，r4=-0.068 1，r5=-0.099 7。根据式(7)可搭建所预测的位移速度在状态空间的概率分布向量。对于每个向量来说，其最大元素所在列对应状态即该阶加权马尔科夫链预测未来位移速度最可能状态，结果见表2。
表2 各阶加权向量及状态概率分布
Table 2 Each order weight vector and state probability distribution
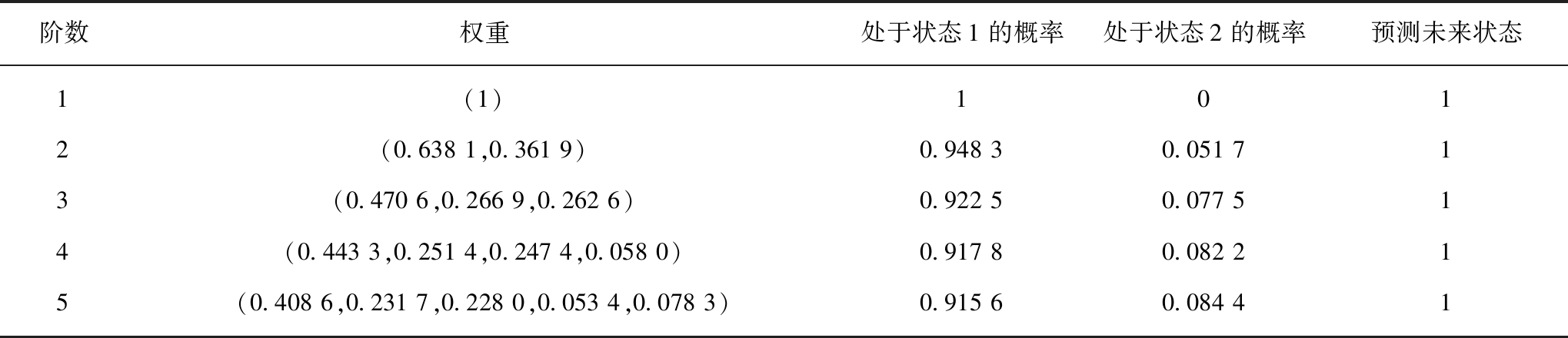
阶数权重处于状态1的概率处于状态2的概率预测未来状态1(1)1012(0.6381,0.3619)0.94830.051713(0.4706,0.2669,0.2626)0.92250.077514(0.4433,0.2514,0.2474,0.0580)0.91780.082215(0.4086,0.2317,0.2280,0.0534,0.0783)0.91560.08441
本实例中，x26=-0.26，聚类后界定其状态为1。即本次预测中，预测与实际相符合。
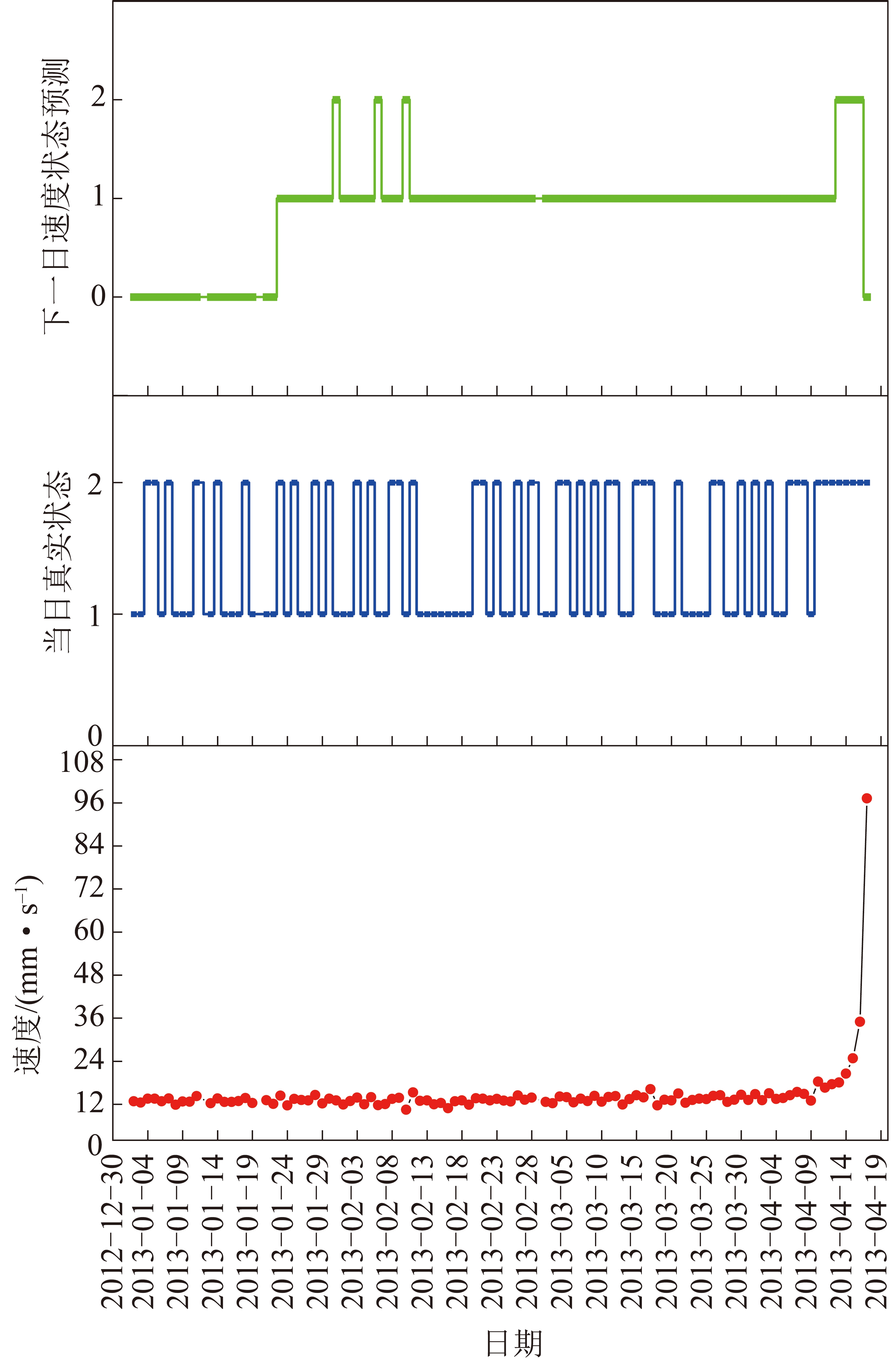
图9 WY2300-512监测点状态预测结果以及预警状况
Fig.9 Status forecasting consequence and warning status of WY2300-512 monitoring point
3.3.3 预测效果评价
利用动态数据捕获，该动态系统将同时采集监测数据和回顾前述预测过程，并将状态预测序列作为验证序列使用。与单一监测相比，该系统可实时反馈真实状态信息和预测状态信息，这两种信息相互印证。另一方面，依据前述预警判据，即可做出是否预防滑坡决策。本实例中，动态加权马尔科夫链的状态预测序列及预警情况如图9所示。
3.4 滑坡预警效果分析及样本容量优化
样本容量选择是动态加权马尔科夫预测的一个关键问题，进而影响滑坡预警的效果。如果样本容量过小，会导致样本的估计参数与理论值相差较大，预计转移矩阵所控制的状态平稳性和概括性不足，可能会影响是否采取滑坡预防工作的判断，使预测敏感度和预警正确率降低，预警可靠性变差;反之，样本容量过大，则期望值与理论值相差较小，会降低模型的敏感性，而导致预警不及时。
为确定最优样本容量，以上述28个监测点为研究对象，对比了不同样本容量(10，15，20，30，40，45，50)下的预警效果。需要说明，在对比预警敏感度时仅考虑了滑坡区域内的监测点，因为此时关注的重点是滑坡预警的及时性;而在对比预警正确率和预测共识率时考虑了所有监测点，因为无论滑坡与否，预警正确率都应该尽可能高，预测共识率也应尽量高。
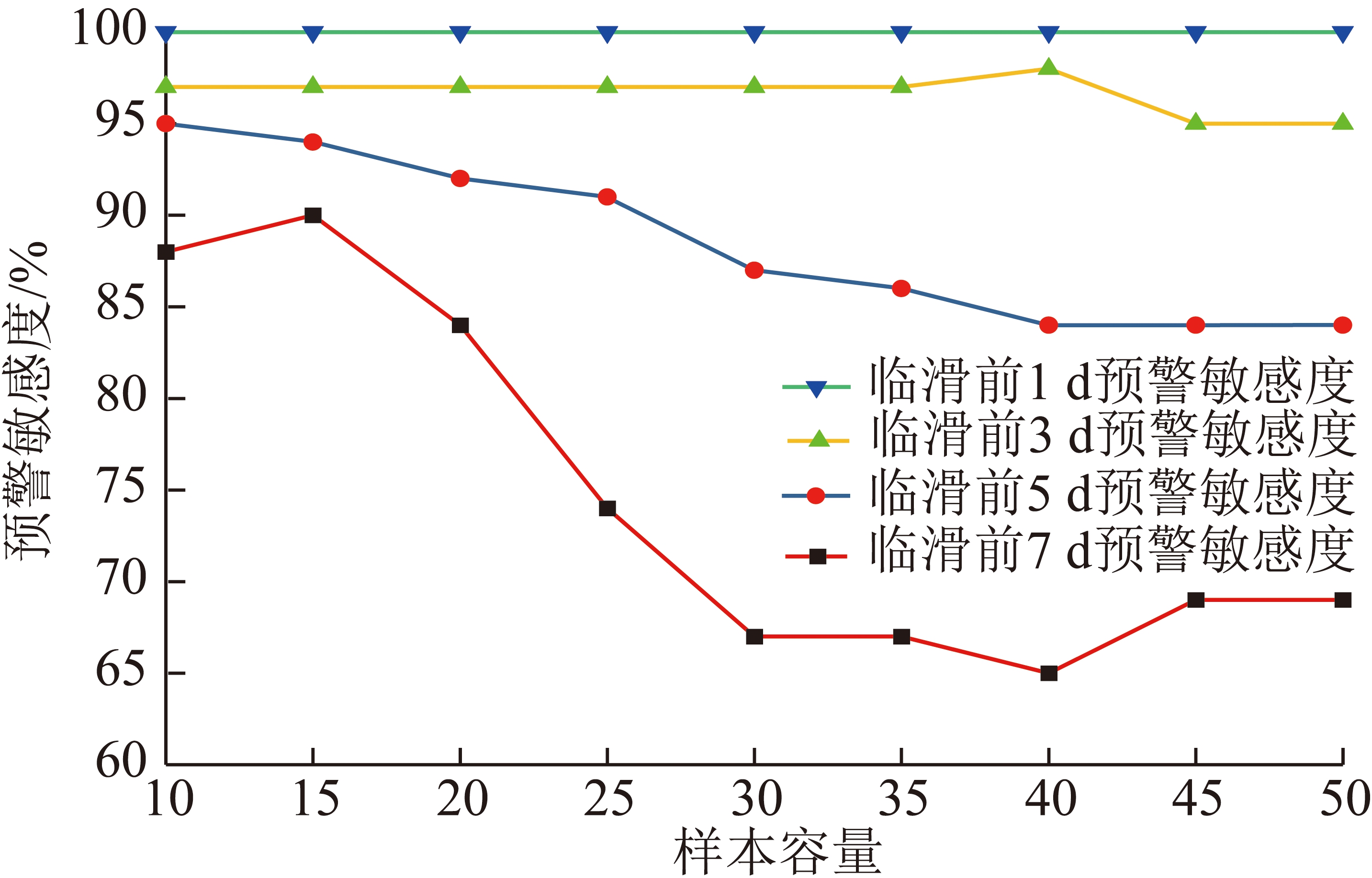
图10 各监测点预警敏感度与样本容量关系曲线
Fig.10 Correlation curves of each monitoring point average landslide early warning sensitivity and sample size
3.4.1 预警敏感度对比分析
通过计算并统计各监测点在不同样本容量下的预警敏感度，可绘制如图10所示的平均预警敏感度与样本容量的关系曲线和如图11所示的平均预警敏感度热点图。显然，对于任一样本容量，随着滑坡的临近，滑坡区内各点的平均预警敏感度在不断提高;临滑前7 d和前5 d的平均预警敏感度均随样本容量增加而降低，表明样本容量增加会在一定程度上降低了模型在临滑前对异常值的敏感度，与模型评价的及时性标准相冲突;当样本容量为10，15，20时，滑坡区域内各监测点的平均预警敏感度均在84%以上，较好的满足了滑坡预警的及时性标准，即是说，从预警敏感度的角度，优选样本容量为10，15，20。
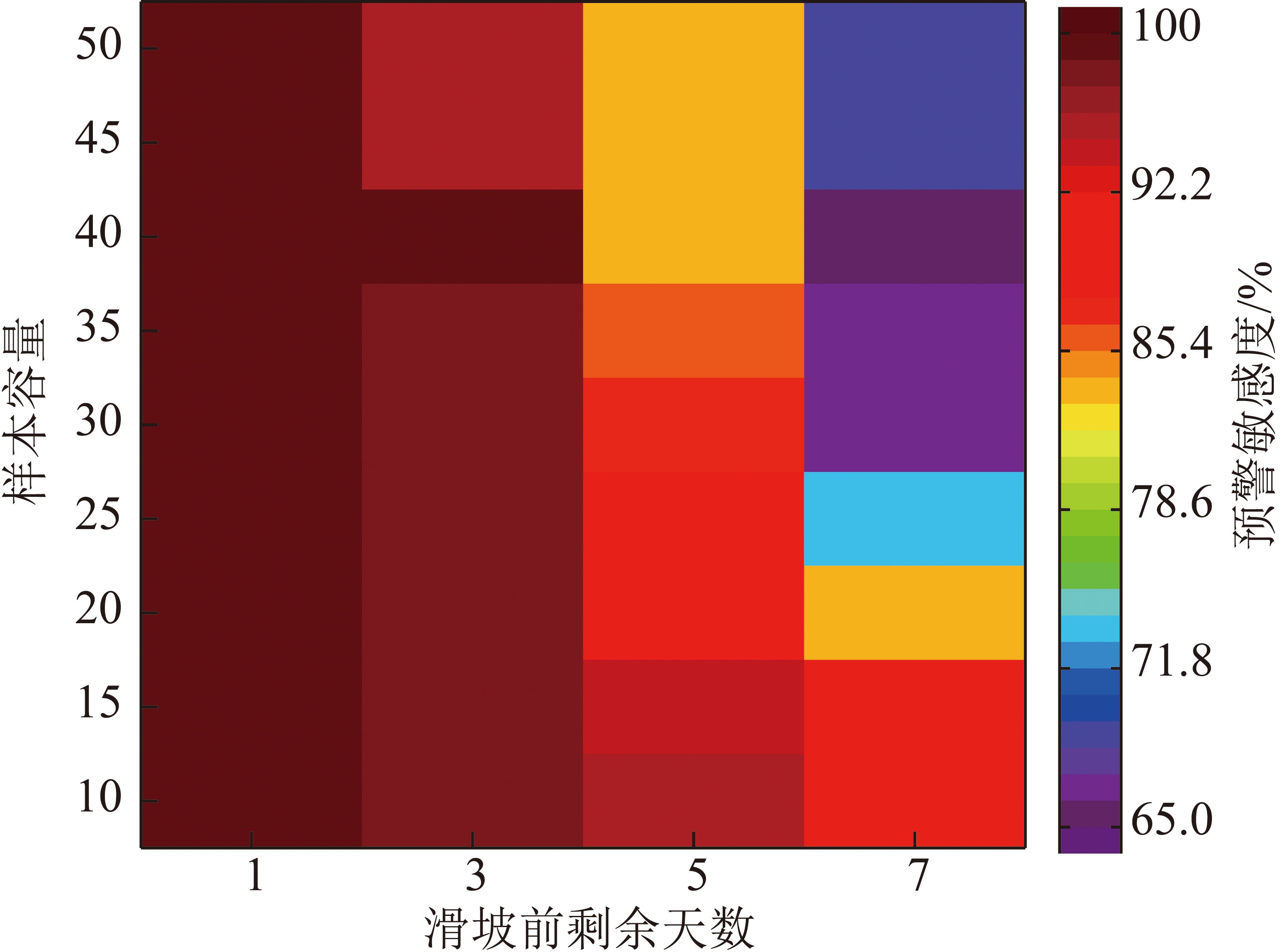
图11 滑坡区域各个监测点平均预警敏感度
Fig.11 Each monitoring average landslide early warning sensitivity in landslide area
3.4.2 预警正确率及预测共识对比分析
通过计算和统计各监测点不同样本容量下的预警正确率和预测共识率，分别绘制了二者与样本容量的关系曲线(图12)。分析可知，平均预警正确率及预测共识率均随样本容量的增大而增高，当样本容量达到20，预测共识率达到70%以上，之后不再有明显的提升空间。结合本文提出的预警有效性评价标准，预警模型在满足规避滞后性和噪声干扰两种有效指标的同时，还应该具有较高的可信度，及模型的最优样本大小参数为20。
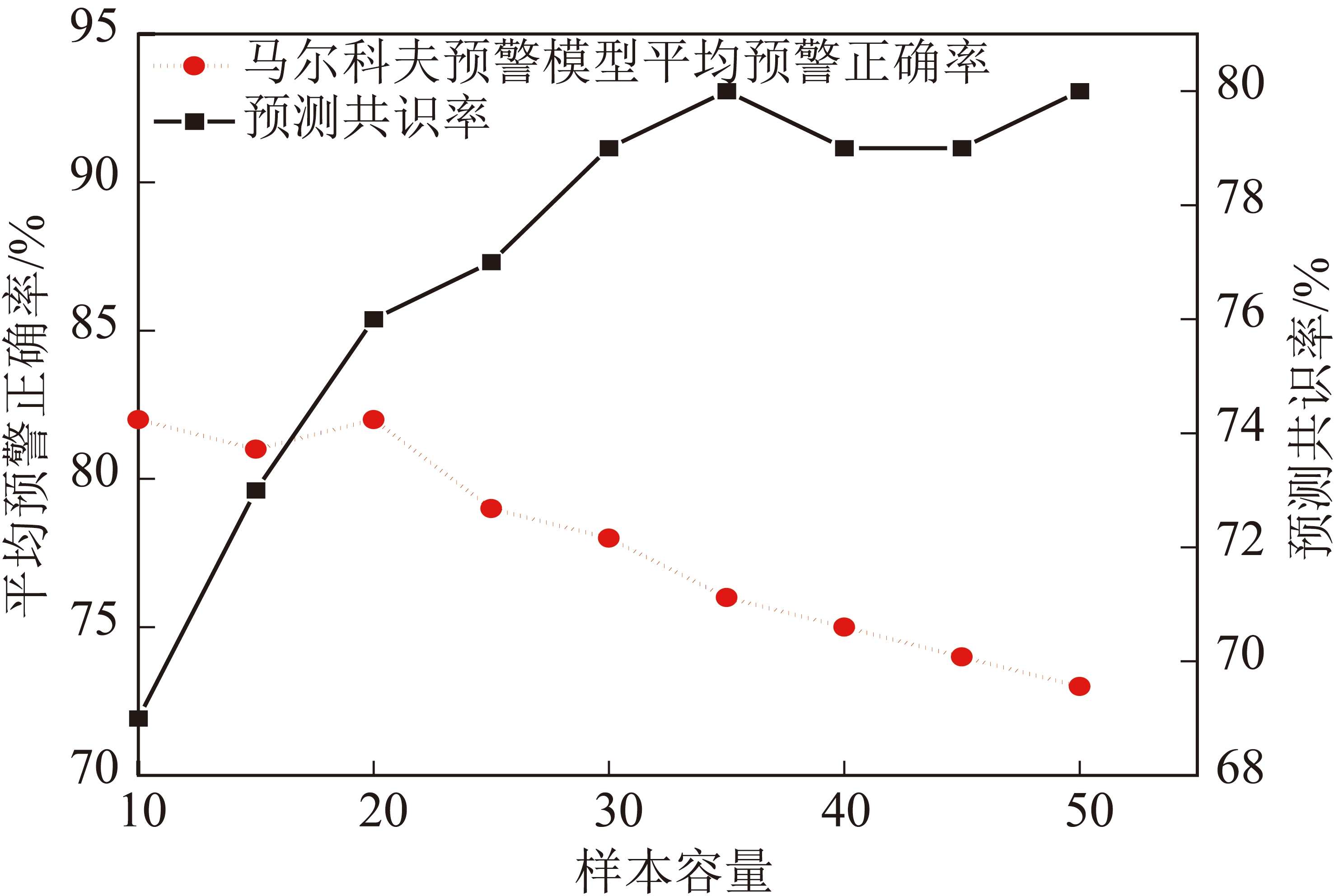
图12 预警正确率、及预测共识率与样本容量的关系曲线
Fig.12 Correlation curves of each monitoring point forewarning correct rate forecast consensus rate
尽管通过对比不同样本容量时预警模型对各监测点的预警结果，确定了基于系统聚类的加权马尔科夫预警模型的最优样本容量，但大部分滑坡不是短期内形成的，必然要经过灾害孕育的发展过程。而前面所开展的研究仅仅侧重于临滑前7 d及时、准确预警的实现，为更好地将预警模型用于滑坡演变过程的描述，统计给出了滑坡区域内外各监测点在滑坡前10 d内的预警判断结果，如图14所示。
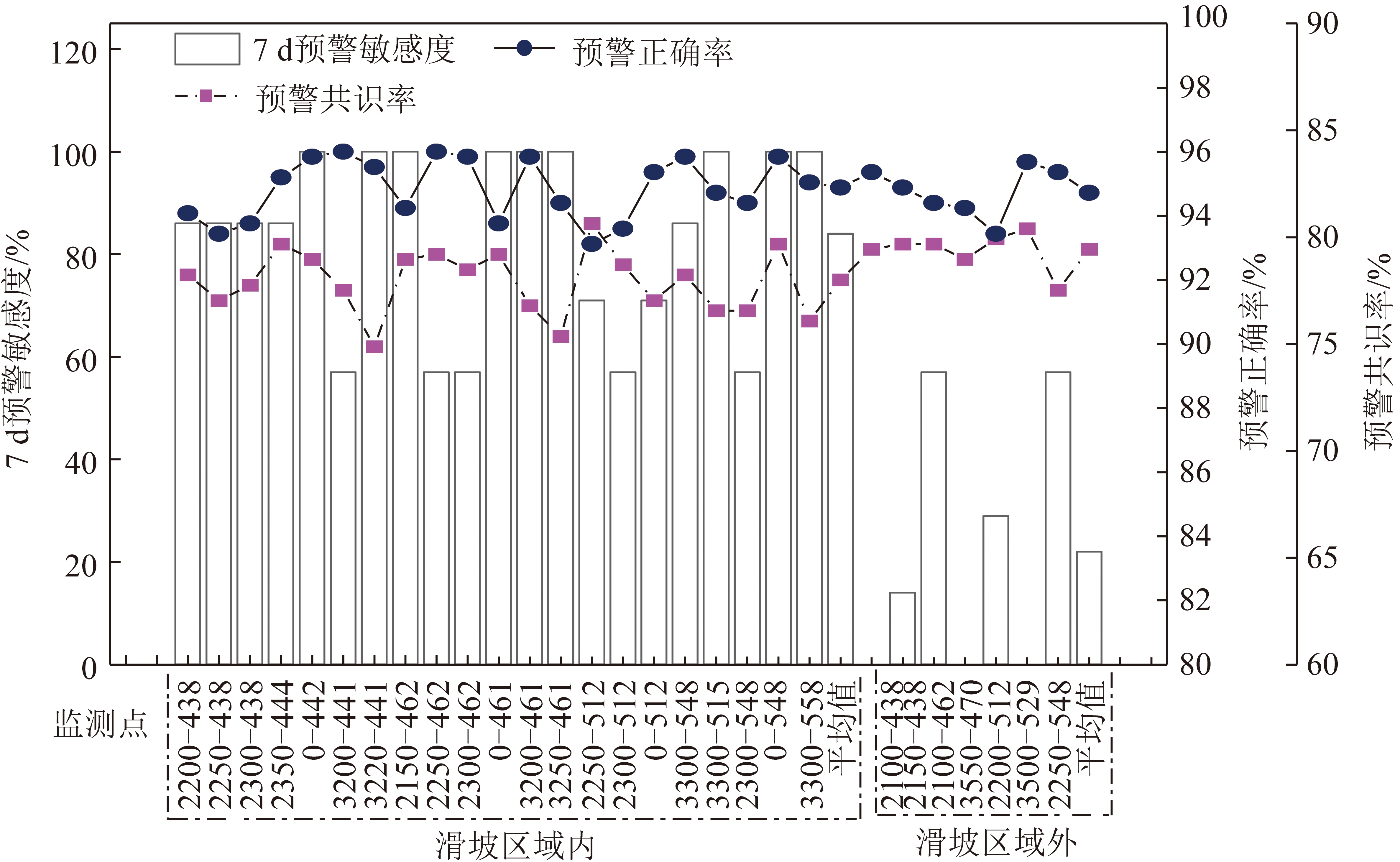
图13 最优模型参数下的预警效果
Fig.13 Forewarning effect figure under optimal model parameters
图14 滑波前各监测点滑坡区内外预警信息
Fig.14 Forewarning warning information outside and within landslides area of each monitoring point before landslide
3.5 滑坡预警模型的后期应用
根据前文所述，本文所用模型在平庄西露天矿的滑坡实例中的应用效果较好，现根据建模及计算过程，对该模型的适用条件进行说明。
本文模型将滑坡位移作为各因素综合作用的输入变量，将位移速率的状态表达作为模型的输出。因此，较为精确的地表位移监测数据是模型建立的前提;但同时，大型工程背景中难以获得的岩土体参数，如地质的几何结构形态、岩土及水文环境参数等，不是模型中的必须变量。所以，该模型本质上是一种单变量预测模型，能充分挖掘单一监测数据的优势，规避了露天矿边坡监测种类少的制约。就监测数据采样的分辨率来说，本文的监测数据为逐日数据，不需要非常密集，因此对于位移测量仪器的工作性能要求不高;同时由本文的最优样本容量可知，监测变量的时间序列长度至少为20 d，这对于普通的监测来说十分容易达到。
4 结 论
(1)与目前流行的露天矿滑坡预警模型相比,该模型将监测设备采集到的位移速度数据划分为正常和异常2种状态，从而实现了速度的状态反馈;临界位移加速度大于0是评价边坡稳定性的一个良好的可靠判据;只有当前日、当日真实反馈的位移速度数据状态与次日位移速度数据预测状态均为异常时才存在滑坡风险。滑坡演化过程中获得的位移参数的随机特性，构建基于马尔科夫理论构建预警方法并提出了基于马尔科夫链理论的滑坡判据，给出预警模型的评价标准。
(2)按照重要程度，从滑坡预警及时性、可靠性以及一致性3方面需求出发，将预警敏感度I、预警正确率W、预测共识率Y作为评价3项指标的标准。当I越接近1时，预警越及时;W越接近1时，预警的可靠性就越高;Y越接近1时，预测状态与真实状态就越接近。
(3)通过对单个监测点的78次预测中发现，预警模型的参数扰动应根据样本容量进行调整。当优选样本容量为20时;预警模型的七日预警敏感度为85%，预警正确率为80%，预警共识率为71%;提高了模型的可靠性。预警模型仅在滑坡前4 d连续给出4次危险警告，表明模型具有较高的预警及时性、抗干扰性及可信度。
(4)建立的预警模型可被认为是一种有效的露天矿滑坡风险缓解措施。适用于位移速度数据采集充分的情形，且所用训练数据也不仅限于位移速度，还可以扩展到位移加速度等。模型的最优参数也需要在验证中进一步确定，从而有助于提高预警模型的效率，以实现滑坡的精密化、分级预警。
[1] KUMAR A,ASTHANA A K L,PRIYANKA R S,et al.Assessment of landslide hazards induced by extreme rainfall event in Jammu and Kashmir Himalaya,northwest India[J].Geomorphology,2017,284:72-87.
[2] CROSTA G B,FRATTINI P,VALBUZZI E,et al.Large slope instabilities in northern Chile:Inventory,characterization and possible triggers[A].Landslide Science for a Safer Geoenvironment[C].Milan,Italy,2014:175-181.
[3] 许强，李为乐，董秀军，等.四川茂县叠溪镇新磨村滑坡特征与成因机制初步研究[J].岩石力学与工程学报，2017，36(11):2612-2628.
XU Qiang,LI Weile,DONG Xiujun,et al.The Xinmocun landslide on June 24,2017 in Maoxian,Sichuan:Characteristics and failure mechanism[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(11):2612-2628.
[4] FAN X M,X Q,RODRIGUEZ AA,et al.Successive landsliding and damming of the Jinsha River in eastern Tibet,China:Prime investigation,early warning,and emergency response[J].Landslides,2019,16(5):1003-1020.
[5] LIANG G H,HU Y,LI Q B.Safety monitoring of high arch dams in initial operation period using vector error correction model[J].Rock Mechanics and Rock Engineering,2018,51(8):2469-2481.
[6] SONG D Q,CHE A L,ZHU R J,et al.Dynamic response characteristics of a rock slope with discontinuous joints under the combined action of earthquakes and rapid water[J].Landslides,2018,15(6):1109-1125.
[7] YIN Y P,WANG H D,GAO Y L,et al.Real-time monitoring and early warning of landslides at relocated Wushan Town,the Three Gorges Reservoir,China[J].Landslides,2010,7(3):339-349.
[8] GUO Z Z,YIN K L,GUI L,et al.Regional rainfall warning system for landslides with creep deformation in Three Georges using a statistical black box model[J].Scientific Reports,2018,9:8962-8976.
[9] SAITO M.Forecasting the time of occurrence of a slope failure[A].Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering[C].Monteral,1965:537-541.
[10] KAWAMURA K.Methodology for landslide prediction[A].Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering[C].San Francisco,1985:12-16.
[11] 蒋平.基于回归神经网络的滑坡位移时间序列预测研究[D].武汉:华中科技大学，2017.
JIANG Ping.Research on prediction of landslide displacement time series based on recurrent neural network[D].Wuhan:Huazhong University of Science and Technology,2017.
[12] WU H,SONG T.An evaluation of landslide susceptibility using probability statistic modeling and GIS’s spatial clustering analysis[J].Human and Ecological Risk Assessment,2018,24(7):1952-1968.
[13] MALAMUD B D,TURCOTTE D L,GUZZETTI F,et al.Landslide inventories and their statistical properties[J].Earth Surface Processes and Landforms,2004,29(6):687-711.
[14] HUANG F M,YIN K L,ZHANG G R,et al.Landslide displacement prediction using discrete wavelet transform and extreme learning machine based chaos theory[J].Environmental Earth Sciences,2016,75(20):1376-1394.
[15] HUANG F M,HUANG J S,JIANG S H,et al.Landslide displacement prediction based on multivariate chaotic model and extreme learning machine[J].Engineering Geology,2017,218:173-186.
[16] LI H J,XU Q,HE Y S,et al.Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models[J].Landslides,2018,15(10):2047-2059.
[17] GOETZ J N,BRENNING A,PETSCHKO H,et al.Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling[J].Computers & Geosciences,2015,81:1-11.
[18] SHIRZADI A,SOLAIMANI K,ROSHAN M H,et al.Uncertainties of prediction accuracy in shallow landslide modeling:Sample size and raster resolution[J].Catena,2019,178:172-188.
[19] LI D,ZAVAGLIA M,WANG G Y,et al.Discrimination of the hierarchical structure of cortical layers in 2-photon microscopy data by combined unsupervised and supervised machine learning[J].Scientific Reports,2018,9:7424-7440.
[20] SLAVKOV I,GJORGJIOSKI V,STRUYF J,et al.Finding explained groups of time-course gene expression profiles with clustering trees[J].Molecular Biosystems,2010,6(4):729-740.
[21] ROSTORFER R L.A cluster analysis of precalculus student performance on function translation fluency test items[D].State of Tennessee:Middle Tennessee State University,2014.
[22] ARGÜELLES M,BENAVIDES C,FERN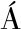
NDEZ.A new approach to the identification of regional clusters:Hierarchical clustering on principal components[J].Applied Economics,46(21):2511-2519.
[23] YANAGIDA R,TAKAGI N.Consideration on hierarchical cluster analysis based on connecting adjacent hyper-rectangles[A].2005 IEEE International Conference on Systems,Man and Cybernetics[C].Waikoloa,2005:2795-2800.
[24] DAVID F.Markov chains[M].New York:Springer,1983.
[25] 骆振福，陈尚龙，赵跃民，等.基于马尔可夫理论的气固分选流化床密度的预测[J].煤炭学报，2011,36(1):105-109.
LUO Zhenfu,CHEN Shanglong,ZHAO Yuemin,et al.Density prediction of gas-solid fluidized bed for separation base on Markov theory[J].Journal of China Coal Society,2011,36(1):105-109.
[26] FRANCISCO D N N,CL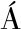UDIO D S B,CLAUDIO E C C.Combining Markov model and prediction by partial matching compression technique for route and destination prediction[J].Knowledge-Based Systems,2018,154:81-92.
[27] 李聪，朱杰兵，汪斌，等.滑坡不同变形阶段演化规律与变形速率预警判据研究[J].岩石力学与工程学报，2016，35(7):1407-1414.
LI Cong,ZHU Jiebing,WANG Bin,et al.Critical deformation velocity of landslides in different deformation phases[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1407-1414.
[28] 许强，曾裕平，钱江澎，等.一种改进的切线角及对应的滑坡预警判据[J].地质通报，2009，28(4):501-505.
XU Qiang,ZENG Yuping,QIANG Jiangpeng,et al.Study on a improved tangential angle and the corresponding landslide pre-warning criteria[J].Geological Bulletin of China,2009,28(4):501-505.
[29] 王东，曹兰柱，朴春德，等.基于假设检验原理边坡临滑时刻动态识别[J].岩石力学与工程学报，2012，31(3):577-585.
WANG Dong,CAO Lanzhu,PIAO Chunde,et al.Dynamic indentification method of slope impending landslide moment based on hypothetic testing theory[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(3):577-585.
[30] 刘璞，王萌，马芩，等.灰色马尔可夫预测模型和加权加增长率移动平均法预测精度的比较[J].统计与决策，2018,22:11-15.
LIU Pu,WANG Meng,MA Qin,et al.Comparison of prediction accuracy between gray Markov forecasting model and weighted plus growth rate moving average method[J].Statistics & Decision,2018,22:11-15.
[31] 吴顺川,刘芳标，周喻，等.岩体节理产状系统聚类与边坡失稳模式分析[J].北京科技大学学报，2014,36(1):1-7.
WU Shunchuan,LIU Fangbiao,ZHOU Yu,et al.Hierarchical cluster of rock mass joint attitude and analysis of slope instability modes[J].Journal of University of Science and Technology Beijing,2014,36(1):1-7.
[32] 曹兰柱，王珍，王前领，等.加权马尔可夫链滑坡预警模型优化研究[J].安全与环境学报，2018，18(3):1030-1035.
CAO Lanzhu,WANG Zhen,WANG Qianling,et al.Approach to optimizing the early warning model via the weighted Markov Chain theory[J].Journal of Safety & Environment,2018,18(3):1030-1035.
[33] 曹兰柱，王珍，王东，等.露天矿滑坡预警理论与方法研究[J].中国安全科学学报，2017，27(3):163-168.
CAO Lanzhu,WANG Zhen,WANG Dong,et al.Research on theory and method of landslide early warning in open-pit mine[J].China Safety Science Journal,2017，27(3):163-168.
[34] 徐传胜.圣彼得堡概率学派的大数定理理论探析[J].西北大学学报(自然科学版)，2011，41(4):727-732.
XU Chuansheng.To systematically analyze the St.Petersburg School of Probability theorem of large numbers[J].Journal of Northwest University(Natural Science Edition),2011,41(4):727-732.
[35] 李秀珍.滑坡灾害的时间预测预报研究[D].成都:成都理工大学，2004.
LI Xiuzhen.Study on time prediction and evaluation of landslide hazard[D].Chengdu:Chengdu University of Technology,2004.
[36] 殷坤龙.滑坡灾害预测预报研究[M].武汉:中国地质大学出版社，2004.
[37] 王东.露井联采逆倾边坡岩移规律及稳态分析研究[D].阜新:辽宁工程技术大学，2010.
WANG Dong.Study on movement rule and stability analysis of counter-tilt slope under combined surface and underground[D].Fuxin:Liaoning Technical University,2010.
[38] 肖玉峰.平庄西露天煤矿滑落区回采关键技术研究[D].包头:内蒙古科技大学，2014.
XIAO Yufeng.Research on the key techniques of extraction to West Open-pit mine landslides areas in Pingzhuang[D].Baotou:Inner Mongolia University of Science & Technology,2014.
