综放开采中关键工艺放煤自动化的实现不仅可以提高综放工作面顶煤的采出率,而且保障了放煤工人的人身安全[1],而垮落煤岩的识别为实现放煤自动化提供理论依据[2]。通过对比不同煤岩界面识别方法,得出基于垮落煤岩冲击液压支架后尾梁的振动信号的识别方法适用于综放工作面垮落煤岩的识别[3]。由于该振动信号为非平稳随机信号,传统的特征——时域特征或频域特征不能完整准确地表达垮落煤岩。近年来,学者以该振动信号的时频特征来表征垮落煤岩,应用于垮落煤岩识别的主要的时频处理方法有小波包变换[4-6],Hilbert变换[7]与EMD[8-9]等,均取得有效的特征向量来表征垮落煤岩,得到识别率较高的垮落煤岩分类模型。然而,以上的垮落煤岩识别方法均未考虑煤岩识别的实时性与综放开采的效率。综放开采的工艺流程为:采煤机采煤—前刮板输送机运煤—移动液压支架—推前刮板输送机—拉后刮板输送机—放顶煤—下一循环。因此,综放开采是一个连续的循环过程。然而传统的垮落煤岩分类模型建立在对该模型的不断训练,分类模型的训练耗时较长,影响综放开采的效率。本文提出通过有效方法直接对比原始数据与未知样本的特征,实现垮落煤岩分类模型的实时建立,该方法可以避免对综放开采效率的影响,只需考虑垮落煤岩识别的有效性与实时性。
笔者提出了一种基于EEMD和KPCA的垮落煤岩特征提取方法,通过对振动信号进行EEMD分解,得到一组IMFs;然后以IMF能量和IMF样本熵构造表征垮落煤岩的特征向量,并利用KPCA分别对这些特征向量的维数进行约简,得到了表征垮落煤岩的实时有效特征向量。提出了一种基于EEMD-KPCA和KL散度的垮落煤岩识别方法,基于EEMD和KPCA提取的有效特征向量,利用KL散度对比“未知样本”与垮落煤岩两类样本,从而实现垮落煤岩模型的快速建立和垮落煤岩的实时有效识别。
1 基于EEMD-KPCA的特征提取
1.1 EEMD基本原理
针对经验模态分解(EMD)存在模态混叠的缺点,EEMD方法利用白噪声频谱均匀性和零均值的特点,通过多次把白噪声加入原信号,对含噪信号进行EMD,对得到的IMF叠加求平均,以此来平滑奇异点的影响[10-11]。具体的分解步骤如下:
(1)在原信号x(t)中加入均值为0,标准差为常数的白噪声n(t),得到含噪信号x′(t):
x′(t)=x(t)+n(t)
(1)
(2)对含噪信号x′(t)进行EMD分解,得到一组IMFs记为ci(t)和一个余项r(t):
![]()
(2)
式中,ci(t)为含噪信号EMD分解后的第i个IMF;n为IMF的个数。
(3)重复第(1),(2)步m次,将m次对应的IMF叠加并取平均,作为原信号EEMD后最终的IMF,记为Ci(t),其中i=1,2,…,n。
![]()
(3)
式中,![]() 为原信号x(t)第j次加入白噪声经EMD得到的IMFs。
为原信号x(t)第j次加入白噪声经EMD得到的IMFs。
为获得表征原信号的特征向量,对EEMD得到的IMFs进一步分析,分别计算各个IMF的能量、峭度和样本熵,并对这3个特征向量的有效性进行比较。具体的计算方法如下:
第i个IMF的能量Ei为
![]()
(4)
式中,xi(k)为第i个IMF序列第k个离散点幅值;o为IMF序列总的采样点数。
然后以归一化的各个IMF能量构造特征向量P
![]()
(5)
第i个IMF的峭度Ki为
![]()
(6)
式中,μi和σi分别为第i个IMF的均值和标准差。
然后以归一化的各个IMF峭度构造特征向量Q
![]()
(7)
样本熵[12-13]用来度量各个IMF序列的复杂度,第i个IMF的样本熵表示为Si,样本熵的具体计算方法见文献[12]。
然后以归一化的各个IMF熵构造特征向量R
![]()
(8)
式(5),(7)和(8)中的n为IMF序列的个数。
1.2 KPCA基本原理
核主成分分析[14-15](KPCA)的基本原理:首先通过非线性映射把原始数据空间映射到高维特征空间中,然后在高维特征空间进行主成分分析,从而得到原始数据的低维特征。
设原始数据集为X={x1,x2,…,xk,…,xM},其中xk∈RN,M为原始数据集样本个数。现引入非线性映射Φ,使原始数据空间X中的样本点xk映射到高维特征空间Y中的样本点Φ(xk),并假设![]() 则高维特征空间Y中的协方差矩阵为
则高维特征空间Y中的协方差矩阵为
![]()
(9)
因此,对特征空间Y中的数据集(样本点集)进行主成分分析就是求解方程
λν=Cν
(10)
中的特征值λ和特征向量ν。由于特征向量ν∈Y,因此,特征向量ν可由特征空间Y中的样本点集Φ(xk)(k=1,2,…,M)线性表示为
![]()
(11)
式中,αi为与Φ(xi)对应的系数。
式(10)两边左乘Φ(xk)得到
λ(Φ(xk)ν)=Φ(xk)Cν
(12)
将式(9),(11)代入式(12),并令Kij=(Φ(xi)·Φ(xj)),i,j=1,2,…,M,得
MλKα=K2α
(13)
化简得
Mλα=Kα
(14)
通过对式(14)的求解,即可获得要求的特征值和特征向量。对于测试样本Φ(x)在νk上的投影:
![]()
(15)
其中,![]() 为第k个特征向量,则gk(x)为对应于Φ(x)的第k个非线性主成分。
为第k个特征向量,则gk(x)为对应于Φ(x)的第k个非线性主成分。
2 基于KL散度的特征对比
2.1 KL散度
KL散度[16-17](Kullback-Leibler divergence)用来度量两个概率分布的相似程度,其定义为
![]()
(16)
其中,p和q为概率空间Ω下的两个概率分布。DKL(p‖q)值越小,表示两个分布越接近,反之越相异。
2.2 基于KL散度的特征对比
分别计算顶煤垮落样本和岩石垮落样本的特征向量并归一化,记为概率空间Ω下的概率分布p1和p2,以同样特征提取方法获得“未知样本”的概率分布q,分别计算DKL(p1‖q)和DKL(p2‖q),比较2个KL散度值的大小,从而确定“未知样本”的类别,实现垮落煤岩的识别。并比较垮落煤岩样本和“未知样本”不同特征向量的KL散度值差异,从而确定较有效的表征垮落煤岩的特征向量。
3 垮落煤岩识别
3.1 整体思路及振动信号的采集
针对传统垮落煤岩识别方法影响综放开采效率的技术问题,提出了一种基于EEMD-KPCA和KL散度的垮落煤岩识别方法,该识别方法的具体流程如图1所示。该识别方法不仅综合考虑垮落煤岩识别的有效性与实时性,利用EEMD和KPCA快速有效地提取表征垮落煤岩的特征向量,而且利用KL散度直接对比原始数据与未知样本的特征,从而可以避免对综放开采效率的影响。
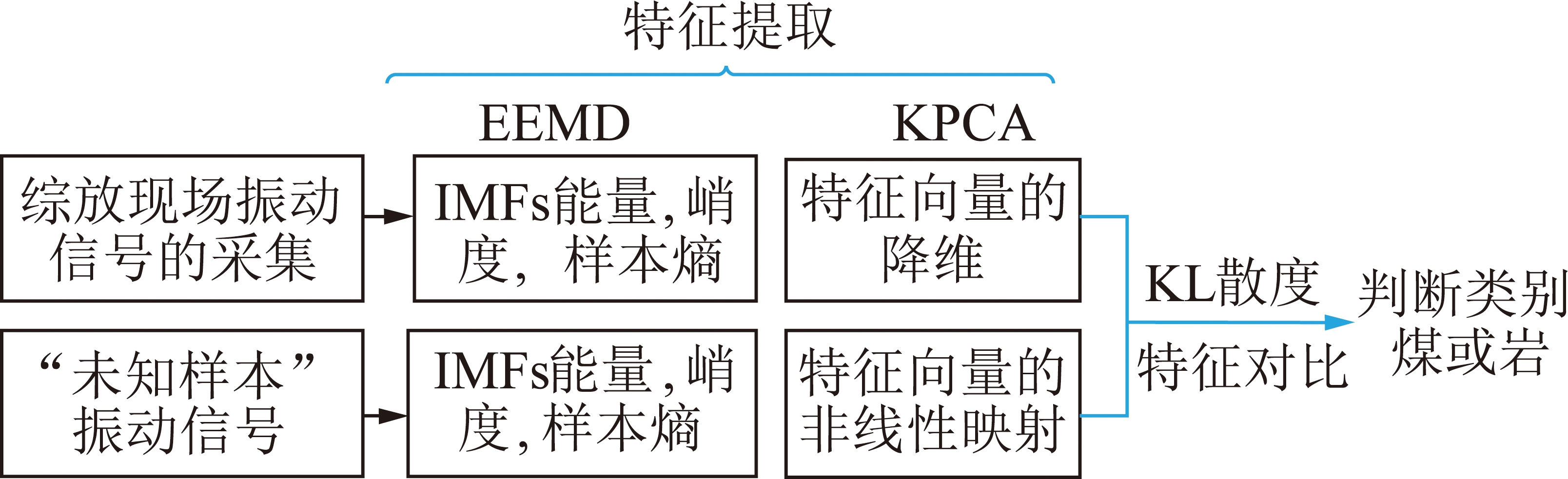
图1 本文垮落煤岩识别方法流程
Fig.1 Flow of collapsing coal-rock identification method proposed in this paper
利用YHJ(C)矿用测振记录仪和GBC1000加速度传感器[18-19],于中煤朔州担水沟煤矿9201综放工作面开展了现场试验,完整地采集了放煤过程中垮落煤岩冲击液压支架后尾梁的振动信号,采样频率为10 kHz,顶煤垮落和岩石垮落两工况下样本的信号长度设为1 s。YHJ(C)矿用测振记录仪布置于液压支架两立柱之间,GBC1000加速度传感器通过磁力吸座吸附于液压支架后尾梁背部,如图2所示。
顶煤垮落样本和岩石垮落样本的时域波形图如图3所示。由图3可得,顶煤垮落时振动信号的振幅范围为-50~50 m/s2,岩石垮落时振动信号的振幅为-100~100 m/s2,两种工况下振动信号的波形有差异;但是,顶煤垮落时的特殊工况(大块顶煤垮落)的振动信号和岩石垮落时的振动信号振幅相同,振动信号的波形差异也较小,难以显著区分,且顶煤垮落和岩石垮落工况下,振动信号的方差会随着振动信号的长度发生变化且无规律可循[19],即两种工况下的振动信号均具有非平稳性。因此,传统的时域特征和频域特征不能完整准确地表征该振动信号。
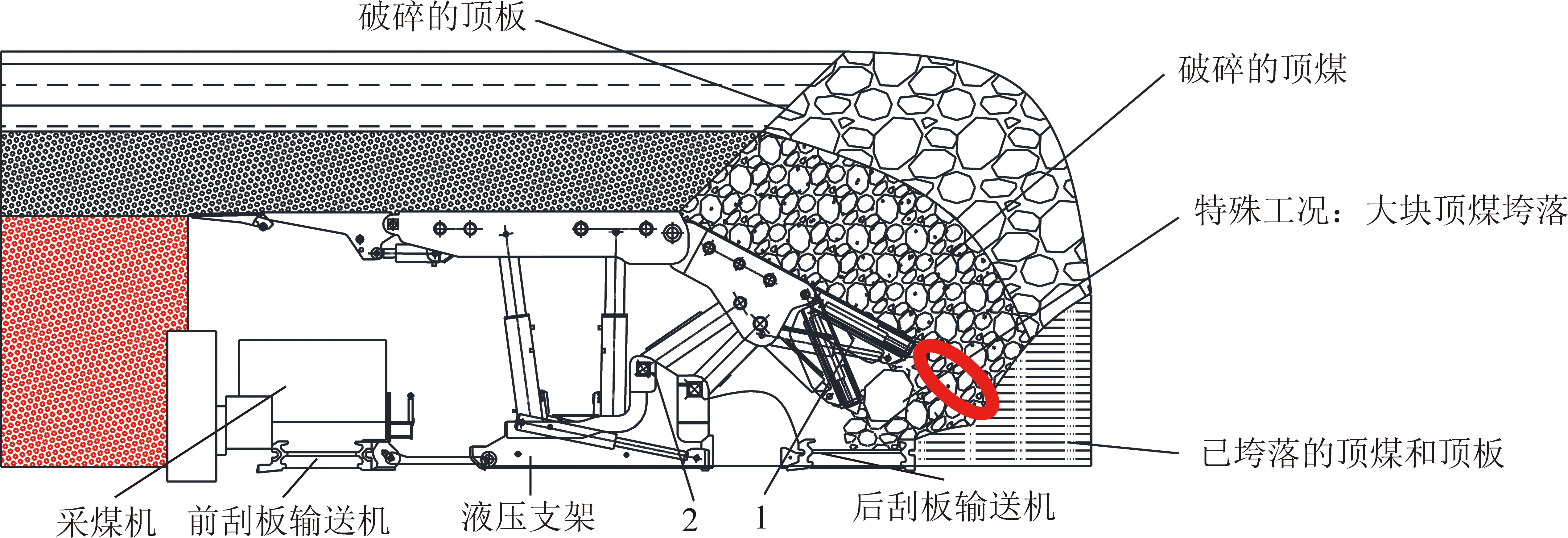
图2 测试仪器布置
Fig.2 Test instruments layout 1—加速度传感器测点;2—测振记录仪布置位置
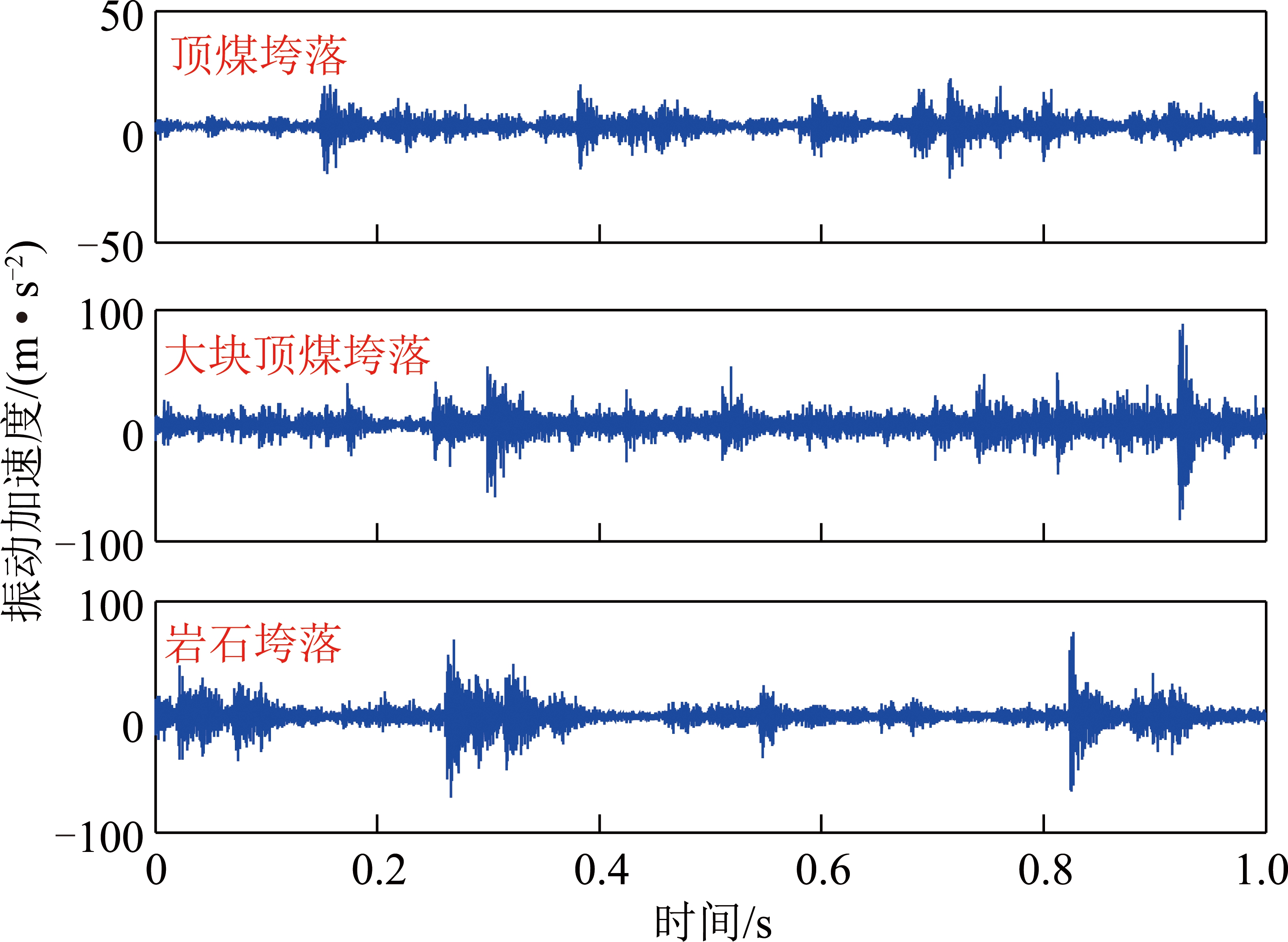
图3 不同工况下的时域波形
Fig.3 Time domain wave of different working conditions
3.2 振动信号的EEMD特征
对顶煤垮落和岩石垮落两类样本进行EEMD分解(循环添加白噪声的次数m=10,白噪声标准差与样本标准差的比值为0.3),得到12组IMF分量,如图4所示,由图4可知,岩石垮落样本的第1个IMF序列的幅值范围是顶煤垮落样本的2倍,岩石垮落样本的第2~4个IMF序列的幅值范围达到顶煤垮落样本的10倍,岩石垮落样本的前5个IMF序列的波形在某一处有明显的冲击振动,之后迅速衰减,而顶煤垮落样本的前5个IMF序列的波形在多处有幅值的变化,两类样本的EEMD分解结果有明显的区分性,尤其在前5个IMF分量,幅值范围和波形均有显著差异。然后,利用式(4),(5)计算100组顶煤垮落样本和100组岩石垮落样本的特征向量P(归一化的IMF能量);利用式(6),(7)计算100组顶煤垮落样本和100组岩石垮落样本的特征向量Q(归一化的IMF峭度);利用文献[12]的计算步骤和式(8)计算100组顶煤垮落样本和100组岩石垮落样本的特征向量R(归一化的IMF样本熵)。
3.3 基于KPCA的特征降维
分别以90组顶煤垮落样本和90组岩石垮落样本的特征向量P,特征向量Q,特征向量R构成高维数据集,利用KPCA(核函数选用高斯核函数)对3个高维数据集进行降维,降维结果如图5所示。
由图5(a)可以看出,由特征向量P构成的高维数据集经KPCA降维后,特征向量的维数为3,顶煤垮落和岩石垮落两类样本在三维空间的分布不同,但是部分顶煤垮落样本和岩石垮落样本重叠,难以区分,即以归一化的IMF能量来表征垮落煤岩识别效果较差;由特征向量Q构成的高维数据集经KPCA降维后,特征向量的维数为5,无法用空间坐标系来表示,以部分样本(顶煤垮落样本和岩石垮落样本各取5个)来观察两类样本的差异性,由图5(b)可以看出以特征向量Q的KPCA低维特征来表征两类样本效果较好,该特征向量的有效性需进一步验证;由特征向量R构成的高维数据集经KPCA降维后,特征向量的维数为4,也无法用空间坐标系来表示,以部分样本(顶煤垮落样本和岩石垮落样本各取5个)来观察两类样本的差异性,由图5(c)可以看出两类样本在该低维特征向量的第2个变量和第3个变量具有明显区别,以该低维特征向量来表征垮落煤岩效果也较好,该特征向量的有效性也需进一步验证。

图4 两类样本的EEMD分解结果
Fig.4 EEMD results of two kinds of samples

图5 特征向量构成的高维数据集的KPCA降维效果
Fig.5 Dimension reduction effect of the high-dimensional datasets composed of feature vector based on KPCA
3.4 基于KL散度的垮落煤岩识别
基于上述特征向量提取方法,分别比较1个“未知落煤样本”和10组顶煤垮落样本及10组岩石垮落样本(共20组样本)的KL散度值,1个“未知落岩样本” 和10组顶煤垮落样本及10组岩石垮落样本(共20组样本)的KL散度值,以上述归一化的特征向量作为概率空间的概率分布,“未知样本”和20组样本的KL散度值的结果对比如图6所示,其中,横坐标为上述的20组样本,1~10组为顶煤垮落样本,11~20组为岩石垮落样本。
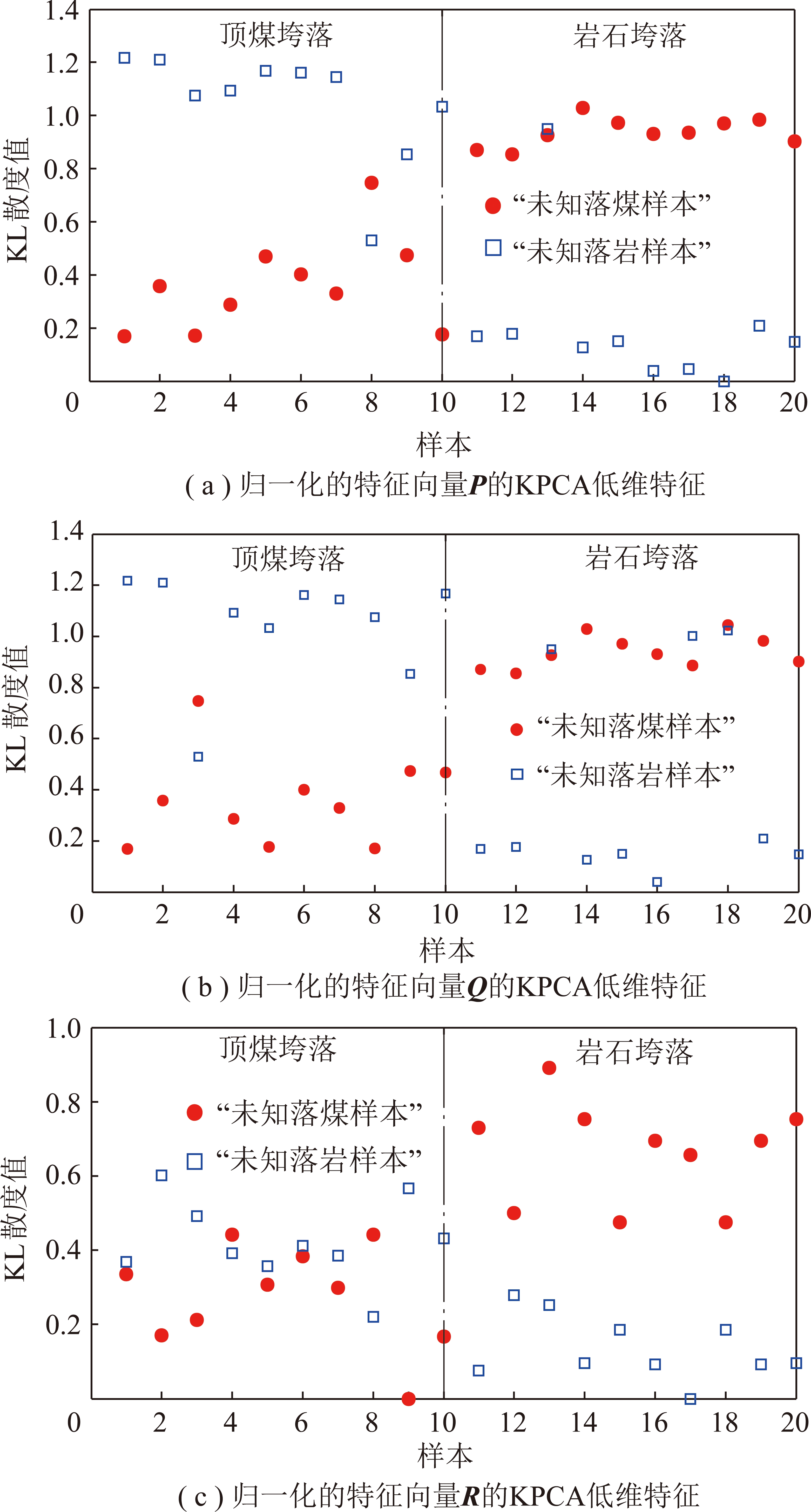
图6 不同特征向量作为两种工况概率分布的KL散度值对比
Fig.6 Comparison of KL divergence values with different eigenvectors as probability distribution of two kinds of working conditions
由图6(a)可知,以归一化的特征向量P的KPCA低维特征为概率分布,“未知落煤样本”和9个顶煤垮落样本的KL散度值小于“未知落煤样本”和岩石垮落样本的KL散度值,即“未知落煤样本”与顶煤垮落样本的分布接近,说明该方法可以准确识别“未知落煤样本”的属性—顶煤垮落,然而,从图6(a)也可以看到“未知落煤样本”和第8个顶煤垮落样本的KL散度值较大,接近于“未知落煤样本”和岩石垮落样本的KL散度值,此时,会误判“未知落煤样本”的属性;同理,“未知落岩样本”和顶煤垮落样本的KL散度值远大于“未知落岩样本”和岩石垮落样本的KL散度值(除了“未知落岩样本”和第3个岩石垮落样本),即“未知落岩样本”与岩石垮落样本的分布接近,说明该方法也可以准确识别“未知落岩样本”的属性—岩石垮落,同样,“未知落岩样本”和第3个岩石垮落样本的KL散度值也极易误判“未知落岩样本”的属性。
由图6(b)可知,以归一化的特征向量Q的KPCA低维特征为概率分布,“未知落煤样本”和顶煤垮落样本的KL散度值均小于“未知落煤样本”和岩石垮落样本的KL散度值,即可以准确识别“未知落煤样本”的属性—顶煤垮落,“未知落煤样本”和第3个顶煤垮落样本的KL散度值接近于“未知落煤样本”和岩石垮落样本的KL散度值,也易造成误判;同理,“未知落岩样本”和顶煤垮落样本的KL散度值均较大,即“未知落岩样本”与顶煤垮落样本的分布差异较大,而“未知落岩样本”和3个岩石垮落样本的KL散度值也较大,此时“未知落岩样本”的属性极易误判,该方法用来识别“未知落岩样本”不是很有效。
由图6(c)可知,以归一化的特征向量R的KPCA低维特征为概率分布,“未知落煤样本”和顶煤垮落样本的KL散度值均小于“未知落煤样本”和岩石垮落样本的KL散度值,即可以准确识别“未知落煤样本”的属性—顶煤垮落,但某些的KL散度值差异不大,此时,容易造成误判;同理,“未知落岩样本”和顶煤垮落样本的KL散度值大于“未知落岩样本”和岩石垮落样本的KL散度值,但某些的KL散度值差异不大,此时,“未知落岩样本”的属性也易误判,因此,该方法可以用来识别“未知样本”的属性,但不是很显著。
由于综放开采的放煤过程是一个连续的过程,因此,需要综合考虑放煤过程中垮落煤岩识别的有效性和实时性。且由于综放开采也是一个连续的过程,因此,识别模型的快速建立也可以减少对综放开采效率的影响。
为了考察该垮落煤岩识别方法的实时性,统计了各个特征向量的特征提取耗时和特征对比的耗时,见表1。
表1 本文垮落煤岩识别方法的耗时
Table 1 Time consuming of the collapsing coal-rock identification proposed in this paper

垮落煤岩识别耗时/sIMF能量0.858 3特征提取IMF峭度0.862 5IMF样本熵15.029 3KPCA0.014 5特征对比KL散度0.006 3
由表1可知,IMF能量和IMF峭度的耗时均小于1 s,基本上满足垮落煤岩实时性的要求,而IMF样本熵的耗时有15 s,明显不符合实时性的要求,即该特征提取方法不可取。基于KPCA特征降维耗时仅有0.014 5 s,不影响特征的实时性。而基于KL散度的特征对比耗时也非常短,仅有0.006 3 s,几乎不影响综放开采的效率。综合考虑各个特征向量的有效性和实时性,组合特征向量P和特征向量Q构成特征向量S,并以归一化的特征向量S的KPCA低维特征SL为概率分布,对比“未知落煤样本”,“未知落岩样本”和10组顶煤垮落样本及10组岩石垮落样本的KL散度值,如图7所示。由图7可知,“未知落煤样本”和顶煤垮落样本的KL散度值均远小于“未知落煤样本”和岩石垮落样本的KL散度值,即可以准确识别“未知落煤样本”的属性—顶煤垮落;同样,“未知落岩样本”和岩石垮落样本的KL散度值均远小于“未知落岩样本”和顶煤垮落样本的KL散度值,即可以准确识别“未知落煤岩样本”的属性—岩石垮落。即,由EEMD分解后的各个IMF的能量和峭度构成的向量的KPCA低维特征最有效。
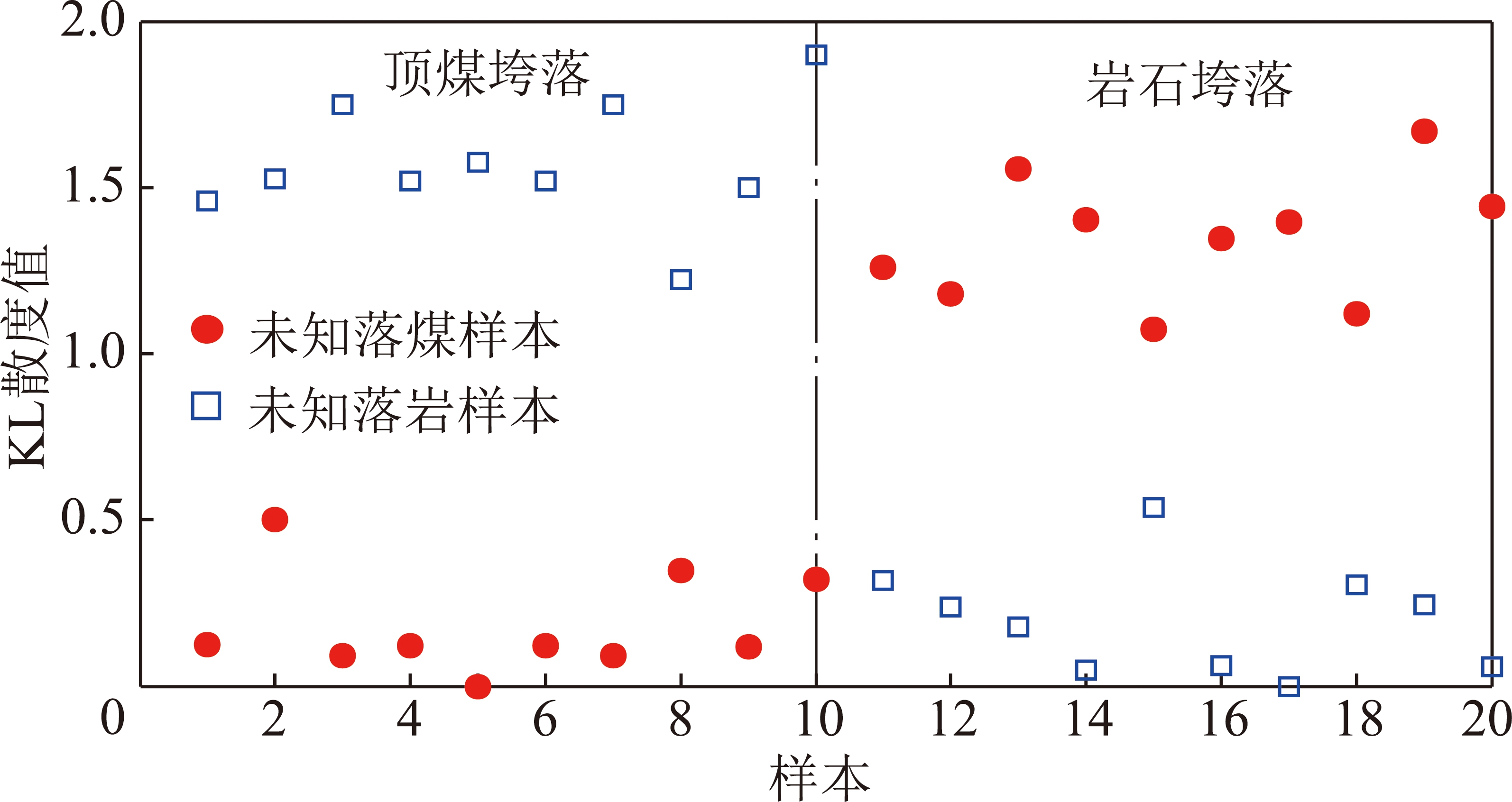
图7 特征向量SL作为两种工况概率分布的KL散度值
Fig.7 KL divergence values with eigenvector SL as probability distribution of two kinds of working conditions
利用BP神经网络[20]来验证该垮落煤岩识别方法的有效性,顶煤垮落样本和岩石垮落样本各取70组作为训练样本,各取20组作为验证样本,并与应用于垮落煤岩识别的时频特征做对比,见表2。
表2 不同输入的BP神经网络训练结果对比
Table 2 Training results of BP neural network using different input vector
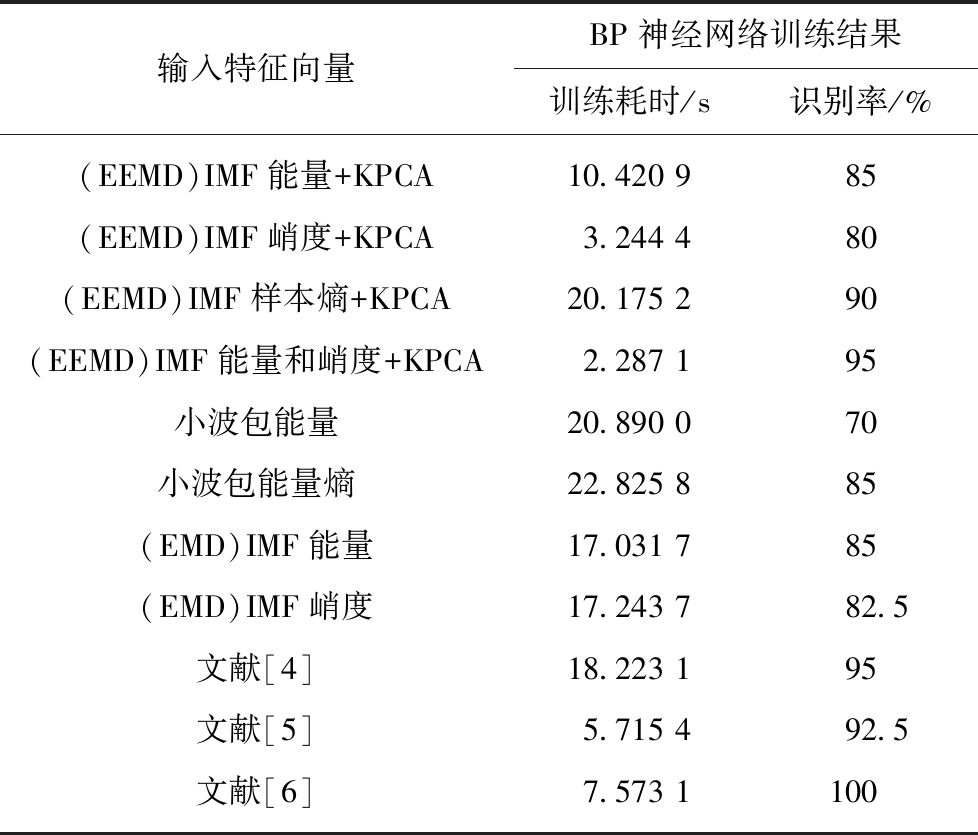
输入特征向量BP神经网络训练结果训练耗时/s识别率/%(EEMD)IMF能量+KPCA10.420 985(EEMD)IMF峭度+KPCA3.244 480(EEMD)IMF样本熵+KPCA20.175 290(EEMD)IMF能量和峭度+KPCA2.287 195小波包能量20.890 070小波包能量熵22.825 885(EMD)IMF能量17.031 785(EMD)IMF峭度17.243 782.5文献[4]18.223 195文献[5]5.715 492.5文献[6]7.573 1100
由表2可知,对于不同输入向量,BP神经网络的训练耗时在2.287 1~22.825 8 s,远远大于基于KL散度的垮落煤岩识别的耗时(0.006 3 s),影响综放开采的效率。对比本文各个提取的表征垮落煤岩的特征向量,EEMD分解后各个IMF的能量和峭度构成的向量的KPCA低维特征识别率大于其余特征向量的识别率,验证了IMF的能量和峭度构成的向量的KPCA低维特征的有效性。并对比该特征与小波包能量,能量熵,IMF能量,IMF峭度和文献[4-6]等特征,BP神经网络的识别率达到95%,除了比文献[6]的识别率低,均高于其他特征,进一步验证了EEMD分解后各个IMF的能量和峭度构成的向量的KPCA低维特征的有效性。
4 结 论
(1)提出了一种基于EEMD和KPCA的垮落煤岩特征信号的特征提取方法,并考虑垮落煤岩识别的实时性,同时对比了各个特征的有效性和特征提取的耗时,从而获得有效的特征向量—EEMD后各个IMF的能量和峭度构成的向量的KPCA低维特征向量。
(2)提出了一种基于EEMD-KPCA和KL散度的垮落煤岩识别方法,不仅考虑垮落煤岩识别的实时性,而且了考虑垮落煤岩识别对综放开采效率的影响,获得了有效的且几乎不影响综放开采效率的垮落煤岩识别模型,该识别模型可以实时地提取表征垮落煤岩的特征向量(耗时小于1 s),可以实时有效地识别垮落煤岩(识别耗时仅需0.006 3 s,同类样本的KL散度值明显小于不同类的KL散度值,具有显著的可分性),并利用BP神经网络验证了该垮落煤岩识别模型的有效性,识别率达到95%。
[1] WANG Jinhua,YU Bin,KANG Hongpu,et al.Key technologies and equipment for a fully mechanized top-coal caving operation with a large mining height at ultra-thick coal seams[J].International Journal of Coal Science & Technology,2015,2(2):97-161.
[2] 李一鸣,符世琛,李瑞,等.垮落煤岩性状识别研究[J].工矿自动化,2017,43(2):24-28.
LI Yiming,FU Shichen,LI Rui,et al.Research on identification of caving coal and rock traits[J].Industry and Mine Automation,2017,43(2):24:28.
[3] 朱世刚.综放工作面煤岩性状识别方法研究[D].北京:中国矿业大学(北京),2014.
ZHU Shigang.Study on coal and rock character recognition method[D].Beijing:China University of Mining & Technology(Beijing),2014.
[4] 李一鸣,符世琛,焦亚博,等.基于分形盒维数和小波包能量矩的垮落煤岩性状识别[J].煤炭学报,2017,42(3):803-808.
LI Yiming,FU Shichen,JIAO Yabo,et al.The collapsing coal-rock identification based on fractal box dimension and Wavelet packet energy moment[J].Journal of China Coal Society,2017,42(3):803-808.
[5] 李一鸣,符世琛,周俊莹,等.基于小波包熵和流形学习的垮落煤岩识别[J].煤炭学报,2017,42(S2):585-593.
LI Yiming,FU Shichen,ZHOU Junying,et al.Collapsing coal-rock identification based on wavelet packet entropy and manifold learning[J].Journal of China Coal Society,2017,42(S2):585-593.
[6] 李一鸣,符世琛,周俊莹,等.基于小波包能量流和LTSA的垮落煤岩特征提取[J].煤炭学报,2018,43(S1):331-337.
LI Yiming,FU Shichen,ZHOU Junying,et al.Feature extraction by wavelet packet energy flow and LTSA in collapsing coal-rock recognition[J].Journal of China Coal Society,2018,43(S1):331-337.
[7] 刘伟,华臻,王汝琳.基于Hilbert谱信息熵的煤矸放落振动特征分析[J].中国安全科学学报,2011,21(4):32-37.
LIU Wei,HUA Zhen,WANG Rulin.Vibrational feature analysis for coal gangue caving based on information entropy of hilbert spectrum[J].China Safety Science Journal,2011,21(4):32-37.
[8] 王保平,王增才,张万枝.基于EMD与神经网络的煤岩界面识别方法[J].振动.测试与诊断,2012,32(4):586-590,688.
WANG Baoping,WANG Zengcai,ZHANG Wanzhi.Coal-rock interface recognition method based on EMD and neural network[J].Journal of Vibration,Measurement & Diagnosis,2012,32(4):586-590,688.
[9] 丛晓妍,王增才,王保平,等.基于EMD与峭度滤波的煤岩界面识别[J].振动.测试与诊断,2015,35(5):950-954,995-996.
CONG Xiaoyan,WANG Zengcai,WANG Baoping,et al.Application of filtering method based on EMD and kurtosis in coal-rock interface recognition[J].Journal of Vibration,Measurement & Diagnosis,2015,35(5):950-954,995-996.
[10] 彭畅,柏林,谢小亮.基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J].振动与冲击,2012,31(20):143-146.
PENG Chang,BO Lin,XIE Xiaoliang.Fault diagnosis method of rolling element bearings based on EEMD,measure-factor and fast kurtogram[J].Journal of Vibration And Shock,2012,31(20):143-146.
[11] 胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报,2012,32(11):106-111,153.
HU Aijun,MA Wanli,TANG Guiji.Rolling bearing fault feature extraction method based on ensembled empiric mode decomposition and kurtosis criterion[J].Proceedings of the CSEE,2012,32(11):106-111,153.
[12] 赵志宏,杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断[J].振动.测试与诊断,2012,(4):640-644,692.
ZHAO Zhihong,YANG Shaopu.Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J].Journal of Vibration,Measurement & Diagnosis,2012,(4):640-644,692.
[13] 向丹,葛爽.基于EMD样本熵-LLTSA的故障特征提取方法[J].航空动力学报,2014,29(7):1535-1542.
XIANG Dan,GE Shuang.Method of fault feature extraction based on EMD sample entropy and LLTSA[J].Journal of Aerospace Power,2014,29(7):1535-1542.
[14] 韩萍,吴仁彪,王兆华,等.基于KPCA准则的SAR目标特征提取与识别[J].电子与信息学报,2003,25(10):1297-1301.
HAN Ping,WU Renbiao,WANG Zhaohua,et al.Sar automatic target recgnition based on kpca criterion[J].Journal of Electronics and Information Technology,2003,25(10):1297-1301.
[15] 曾庆虎,邱静,刘冠军,等.基于KPCA-HSMM设备退化状态识别与故障预测方法研究[J].仪器仪表学报,2009,30(7):1341-1346.
ZENG Qinghu,QIU Jing,LIU Guanjun,et al.Research on equipment degradation state recognition and fault prognostics method based on KPCA-Hidden Semi-Markov Model[J].Chinese Journal of Scientific Instrument,2009,30(7):1341-1346.
[16] 李晓艳,张子刚,张逸石,等.一种基于KL散度和类分离策略的特征选择算法[J].计算机科学,2012,39(12):224-227.
LI Xiaoyan,ZHANG Zigang,ZHANG Yishi,et al.KL-divergence based feature selection algorithm with the separate-class strategy[J].Computer Science,2012,39(12):224-227.
[17] 卢继平,徐兵.基于小波包能量相对熵的配电网单相接地故障区段定位[J].电力系统保护与控制,2012,40(20):26-31,37.
LU Jiping,XU Bing.Single-phase earth fault section location based on wavelet packet energy relative entropy in distribution network[J].Power System Protection and Control,2012,40(20):26-31,37.
[18] 李一鸣.基于非平稳振动信号的综放工作面垮落煤岩识别方法研究[D].北京:中国矿业大学(北京),2018.
LI Yiming.Collapsing coal and rock recognition method based on non-stationary vibration signal in fully mechanized caving face[D].Beijing:China University of Mining & Technology(Beijing),2018.
[19] 薛光辉,赵新赢,柳二猛,等.基于振动信号时域特征的综放工作面煤岩识别[J].煤炭科学技术,2015,43(12):92-97.
XUE Guanghui,ZHAO Xinying,LIU Ermeng,et al.Time-domain characteristic extraction of coal and rock vibration signal in fully-mechanized top coal caving face[J].Coal Science and Technology,2015,43(12):92-97.
[20] 李一鸣,柳二猛,焦亚博,等.基于主元分析与神经网络的垮落煤岩性状识别方法研究[J].煤炭工程,2016,48(6):106-109.
LI Yiming,LIU Ermeng,JIAO Yabo,et al.Collapsed coal-rock identification based on principle component analysis and neural network[J].Coal Engineering,2016,48(6):106-109.
