随着物联网时代的到来，“物联网+”技术已经应用至工业生产的每一个角落，同时也掀起了煤矿领域的第4次技术革命。一些大型煤矿通过组建矿山物联网，形成对煤矿生产的整体感知，组建煤矿生产过程中各类信息的监控和监测系统，实现对生产资源(工作人员、生产设备与物资)的感知与识别，工作环境和位置环境等环境信息的感知与采集，从而实现煤矿生产的自动化、信息化和智能化。但在实际应用中，多数煤矿发现物联网技术在解决生产信息采集的实时性上具有独特的优势，但面对采煤现场恶劣的工作环境和监测信息远距离传送带来的信号失真，物联网技术在保证生产信息的准确性上显得力不从心。
数据融合技术应用各种算法对信息采集系统收集到的信息数据进行融合处理，是当前提高监测信息准确性的有效手段，但当前与煤矿监测数据融合技术相关的文献并不多见。文献[1-2]研究了煤矿监测数据的分析处理技术，但文献的研究重点侧重于煤矿监测数据分类技术;文献[3]将D-S证据理论和RS理论两种算法综合应用融合处理煤矿粉尘监测数据，以实现准确判断工作面粉尘状态的目的，但该算法属决策层数据融合算法，存在着融合过程复杂且融合精度较低的不足;文献[4]探讨了煤矿监测数据融合技术，但内容只局限于当前煤矿监测数据融合算法的介绍，并未给出相关算法的模型和融合数据。多年来，一些专家学者探索着应用多传感器数据融合技术中卡尔曼滤波[5]、模糊证据理论[6]和贝叶斯估计算法[7]等算法融合处理煤矿生产现场的监测数据，但这些算法尽管具有一定的数据融合精度，却无法克服煤矿监测信息穿透煤层带来的强度降低和远距离传输中信号干扰带来的信息失真等技术难题。文献[8]针对离散制造系统复杂多变的生产特点，将分数阶微分算子拓展至分数阶偏微分领域，对离散制造系统中受多重因素影响的监测信息进行融合处理，但该算法存在着多重影响因素难以准确确认和计算过程过于复杂的双重不足。笔者尝试应用分数阶微分算子融合处理应用物联网技术采集的煤矿监测信息数据，并通过煤矿井下瓦斯监测数据的融合处理实例验证算法的准确性和有效性，为提高煤矿监测系统工作的可靠性和管理系统决策的科学性提供理论上的支持。
1 分数阶微分算子
1.1 分数阶微分算子的定义
分数阶微分算子是从整数阶微分方程拓展而来，本质上就是任意阶的分数阶导数。目前，在基本理论研究和工程应用研究领域，比较有名的分数阶微分定义有Grunwald-Letnikov、Riemann-Liouville和Caputo Riesz三种[9]。3种定义中因Grunwald-Letnikov定义容易将函数近似求解，计算过程相对比较简单而被广泛应用，故本文应用基于Grunwald-Letnikov定义的分数阶微分算子融合处理煤矿监测信息。分数阶微分的Grunwald-Letnikov定义为:对于任意实数v，记v的整数部分为[v],假设函数s(t)在区间[a,t]上有n+1阶连续导数，v>0时，n≥[v],则定义信号s(t)的v阶微分为
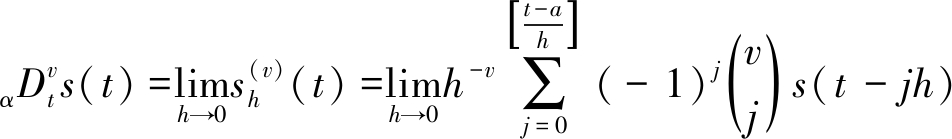
(1)
式中，D为微分处理函数;
为将(t-a)/h的计算值取整数；s(t)的持续时间[a,t]，α为函数微分区间[α,t]的最小值;h为步长值;v为分数阶次，且
是指函数s(t)在步长为h时的v阶微分函数;
为二项式系数;且
(2)
将式(2)代入式(1)可得信号s(t)的v阶微分的最终表达式
(3)
1.2 分数阶微分算子在信号处理中的应用特性
作为分数阶微积分理论的一份子，近年来，分数阶微分算子逐渐受到工程技术人员的高度关注，并将其应用于电化学[10]、材料力学[11]、流体场理论[12]、电磁场理论[13]、生物医学[14]和信号处理[15]等学科领域中，且取得了丰硕的研究成果。经研究发现，分数阶微积分理论适合于研究具有非线性、非因果、非平稳等特征不确定的信号，因此分数阶微积分理论中许多经典算法都非常适合在现代信号分析与处理中应用[16]，下面就开始探讨分数阶微分算子在信号处理中的应用特性。
假设在工程实践中信息采集系统采集到一平方可积的能量信号S(t)，且S(t)∈L2(R)，则可对信号S(t)进行 Fourier变换，得到
(4)
由Fourier变换性质可知:v阶微分算子等于v阶微分乘子函数
的乘性算子，将S(t)分数阶v阶导数记为Sv(t)，可得以下方程
(5)
其中，ω为时域t转换到频域后的角速度;^为函数进行傅里叶变换的固有表达方式，即D的傅里叶变换表示为
为傅里叶变换。
式(5)中令
则可将式(5)简化处理，得
(6)
从上式可以看出，能量信号的分数阶微分处理的本质就是对信号进行滤波处理，滤波函数为
根据滤波函数，绘制如图1所示分数阶微分算子的幅频特性曲线，可以总结出能量信号S(t)经过不同阶次微分处理后具有以下幅频特性[17]:① 分数阶微分算子对能量信号高频部分具有提升作用，提升幅度随着微分算子阶次和信号频率的增加而增加，且呈非线性增长趋势;② 对于能量信号的中低频部分，整数阶微分算子具有削弱作用，而分数阶微分算子(0<v<1)却能对该部分进行不同程度的提升;③ 分数阶微分算子既能加强能量信号的中、高频成分，也能非线性地提升其低频、甚低频成分，具有改善信号强度的功能。
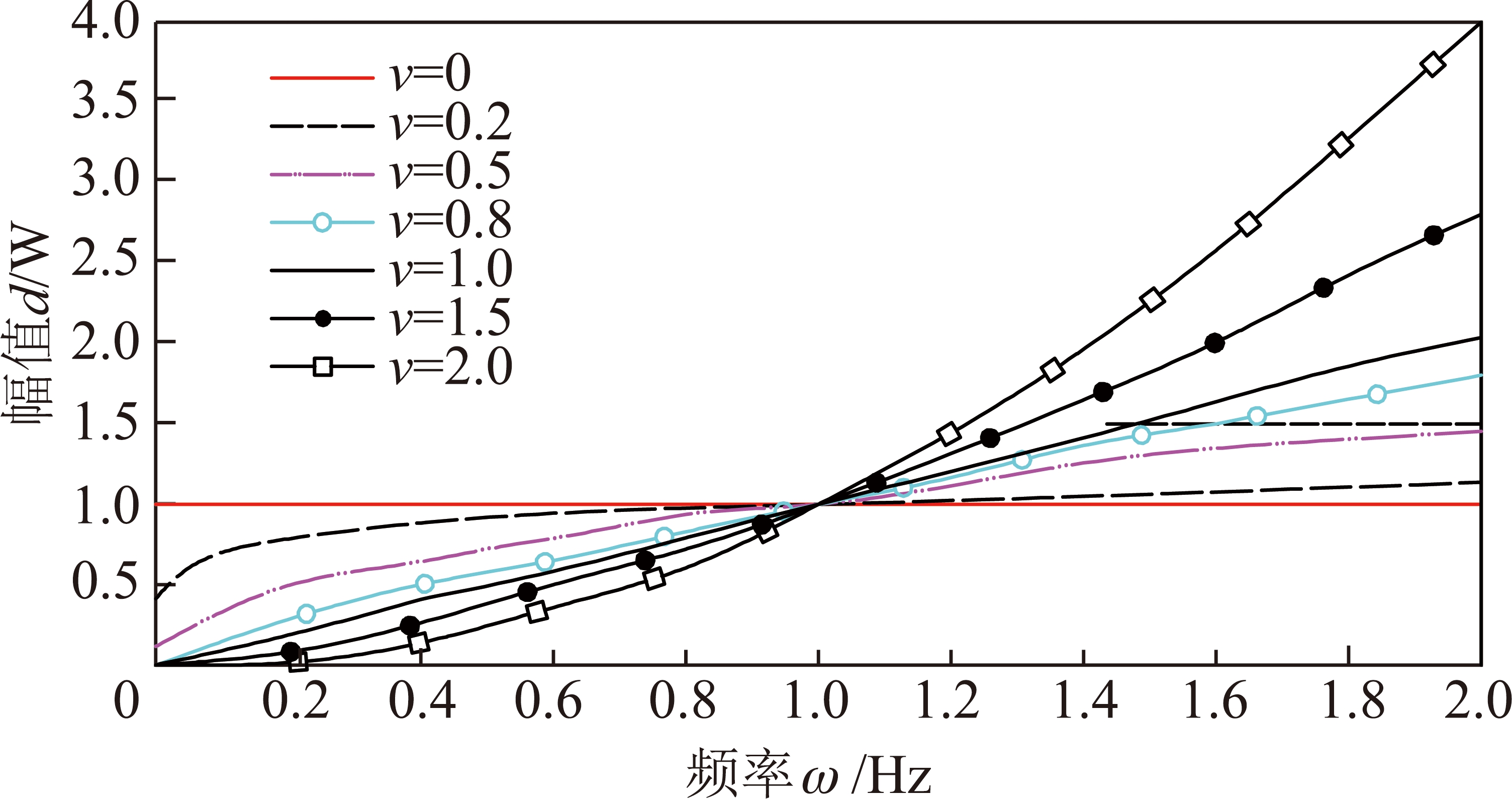
图1 分数阶微分算子的幅频特性曲线
Fig.1 Amplitude frequency characteristic curves of fractional differential operator
2 基于分数阶微分算子的煤矿监测信息的融合处理模型
2.1 信息数据融合处理模型
设煤矿生产信息监测系统应用传感器感知采煤工作面一能量信号E(t)，信号的测量值为Ei(i=1,2,…，n)，并应用物联网技术传送至煤矿生产信息采集中心。因煤矿生产现场环境恶劣，受传感器性能和工作环境的影响，测量值难免存在较大的测量误差;加上信息必须经过穿透几百米地层的远距离传送，信息在传输过程中必然会带来较大的能量损耗，从而致使测量值Ei大幅低于真值。但不论何种影响因素我们都可以用信息测量值的影响因子x来表示，并可以运用Matlab软件找出影响因子xi与测量值Ei之间的关系式E(x),x∈(a,b),其中,a，b为影响因子x的最小值与最大值。
根据Grunwald-Letnikov定义，将采集到的煤矿监测信息E(x)的影响因子x的持续区间(a,b)按步距h均分，则可得n=(b-a)/h。这样就可以得到Grunwald-Letnikov定义下的函数E(x)关于影响因子x的分数阶微分方程:
(7)
其中，G为基于分数阶微分G-L定义的方程式;
为二项式系数，且:
(8)
将式(8)代入式(7)，可得Grunwald-Letnikov定义下基于分数阶微分的煤矿监测信息的数据融合算法模型:
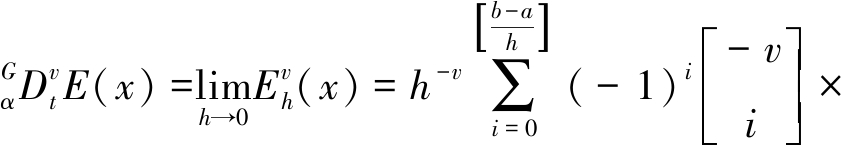
(9)
式中,
为权系数值，其计算公式为
(10)
2.2 监测信息融合处理过程
先应用各类前端监测传感器实现对煤矿生产过程中的各类生产信息的感知与测量，再采用分布式系统下的积分思想[18]对所采集的信息进行分类，评判同类信息数据的有效性。如果采集到的同类数据间偏差值超过了系统设置的公差范围，则应用基于分数阶微分算子的多传感器监测数据融合模型对数据进行融合处理，实现同类数据间的高效融合。最后，应用物联网技术实现对融合后高精度生产信息的实时传输与采集。因此，基于分数阶微分算子的煤矿监测信息数据的融合处理过程为
步骤1:应用测量技术监测煤矿生产系统中由前端传感器感知测量的某一生产信息(如工作面瓦斯浓度)，受传感器性能和工作环境的影响，不同传感器收集到的同一生产信息的数据存在着难以预测的测量误差。
步骤2:评判经不同传感器采集到的生产信息数据之间的误差是否在监测系统设定的误差范围内，如在误差范围内，则向数据采集中心直接发送监测结果，如数据间误差超过系统设定的误差范围，则进入下一步。
步骤3:根据所监测信息的数据属性，选取监测信息测量值的影响因子x;综合各传感器的测量值Ei和相应的影响因子xi，应用MATLAB软件拟合出测量值Ei和影响因子xi之间的函数关系式E(x)。
步骤4:参考监测数据融合模型(式(9))，构建方程E(x)的分数阶微分数据融合模型，并应用MATLAB软件计算各监测数据Ei的分数阶微分处理结果
步骤5:分析比较各监测数据Ei的分数阶微分处理结果
间的误差，评价融合结果。如间的误差在系统设置的范围内，则向数据中心输送融合后的数据。否则，将作为初始值返回步骤3，再次应用分数阶微分算子融合处理，直至最终融合结果间的误差在系统设定范围内。
步骤6:煤矿监测信息的监测数据分数阶微分融合处理过程结束。
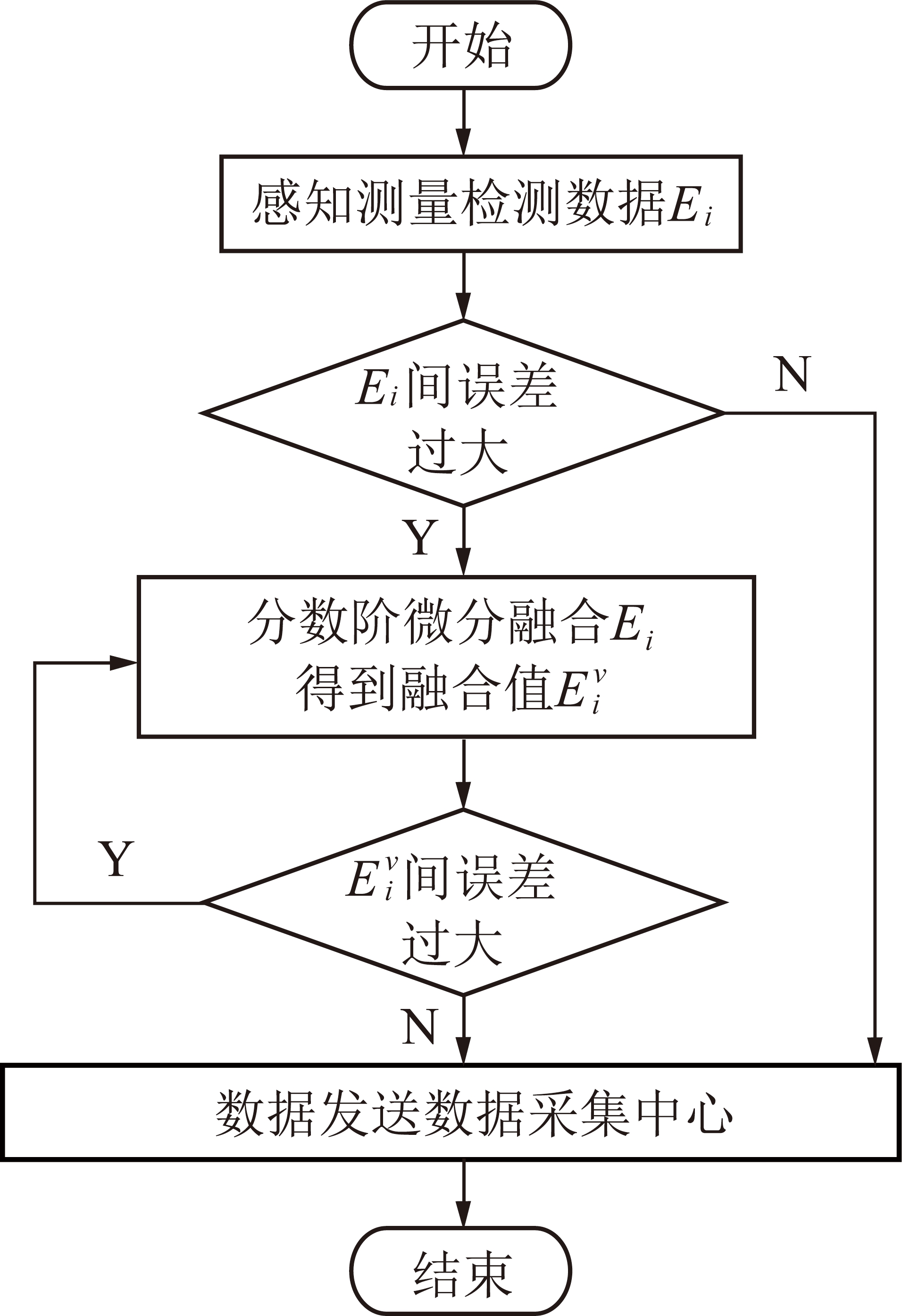
图2 监测数据融合处理过程
Fig.2 Detection fusion procession
3 分数阶微分算子在煤矿监测数据融合处理中的应用
3.1 实验环境
淮南是我国重要的煤炭生产基地，淮南煤矿的突出特点是“高瓦斯”矿井比较多，高瓦斯采煤工作面产量约占全区总产量的70%以上。因此，对于工作面瓦斯的控制一直是确保矿区安全生产的重点和难点。如想实现对工作面瓦斯体积分数的有效控制，首先要做到的就是对工作面瓦斯体积分数的准确测量和监测数据的实时传送，监测数据传输的实时性随着计算机技术的发展已经成功解决，但是由于受到监测仪器性能、工作环境和信号干扰等因素的影响，实现工作面瓦斯浓度的准确测量和远距离传送始终是高瓦斯煤矿安全管理的技术难题。
为了不影响煤矿的正常生产和保证监测系统的工作安全性,本案例采用物联网技术实时采集淮南某矿151302工作面一采煤点的瓦斯体积分数监测值，模拟分数阶微分算子对煤矿工作面瓦斯体积分数监测值的融合处理过程。151302工作面自2015年初开始采煤，经过3 a多的开采刚成为采空区，实验地点位于地下991.0 m，距离主矿井3.75 km处。结合煤矿生产信息采集与传输特点，监测系统在井下应用WIFI无线传输方式将瓦斯体积分数信息传送至主矿井附近的信息采集系统，再通过有线网络将监测信息传送到地面上的煤矿生产信息处理中心。因此，传感器采集到的瓦斯体积分数信息需要通过远距离的井下巷道传送才能到达主矿井附近的数据采集中心。为确保测量值的准确性和监测系统工作的可靠性，实验中应用6只能正常工作的3-2.3V LEL型可燃气体传感器测量该采煤点同一位置的瓦斯体积分数，该测量位置位于采空区且距采煤作业现场近200 m，故采煤作业现场对监测点瓦斯体积分数的影响较小。6只传感器同时工作且每隔5 s测量1次，监测数据经分数阶微分算子快速融合处理后经WIFI实时传送至主矿井下的信息采集中心，6只传感器5次瓦斯体积分数测量数据见表1。
表1 实验数据
Table 1 Experimental data
%
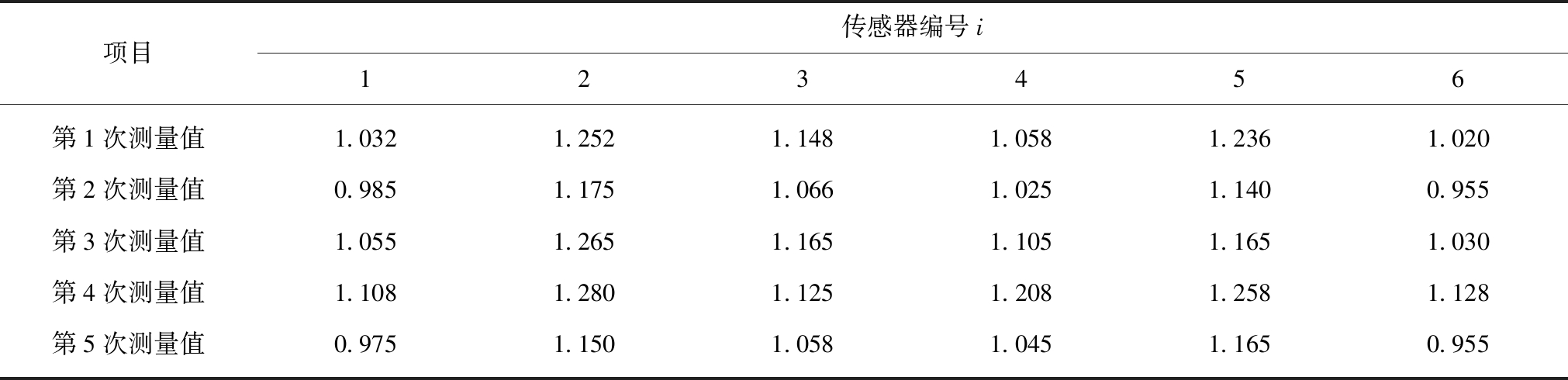
项目传感器编号i123456第1次测量值1.032 1.252 1.1481.058 1.2361.020第2次测量值0.985 1.175 1.0661.0251.1400.955第3次测量值1.055 1.265 1.1651.1051.165 1.030 第4次测量值1.108 1.2801.1251.2081.2581.128 第5次测量值0.975 1.1501.0581.045 1.165 0.955
3.2 数据分析
从3.1节的实验环境可以看出，数据中心接收到的瓦斯体积分数测量值在传感器采集时会受到传感器性能和工作环境等因素的影响，在WIFI传送过程中必将受到复杂的信号干扰和能量衰减带来的监测误差。由表1所示的各传感器在不同时间的测量值可以看出，监测点瓦斯体积分数的测量值是无规律可循的动态变化值，因取样点位于采空区且距采煤作业现场存在近200 m距离，25 s内工作环境的差异性产生突变的可能性较小，故传感器在不同时间点的测量值误差较小;6只传感器放置地点相同，每只传感器监测数据的工作环境和数据采集过程中受到的信号干扰基本相同。因此，本次实验中不同传感器测量值间的差异性主要来自于监测仪器性能的差异性。
实验中将5次测量的平均值
作为各传感器的测量值，所有测量值的平均值作为测量真值E，可以得到物联网下上述监测点瓦斯体积分数测量值的汇总表(表2)和监测数据分布图(图3)。由表2可知，因监测设备间性能存在差异和工作环境较差，同一工作环境下的传感器间测量误差较大，如传感器2的测量值与测量真值E之间测量误差为1.134，远超传感器3的测量误差0.014。从图3所示各传感器监测数据分布曲线可以看出，监测数据并未呈现实验室中测量值在真值附近随机分布的特征，而在测量真值附近呈现无规律的离散分布状态。以上两点可以看出:受监测设备性能和工作环境的影响，煤矿井下监测点瓦斯体积分数的监测值严重失真，很难为煤矿的安全管理提供准确的监测数值，严重影响着安全管理系统决策的科学性。
表2 实验数据
Table 2 Experimental data
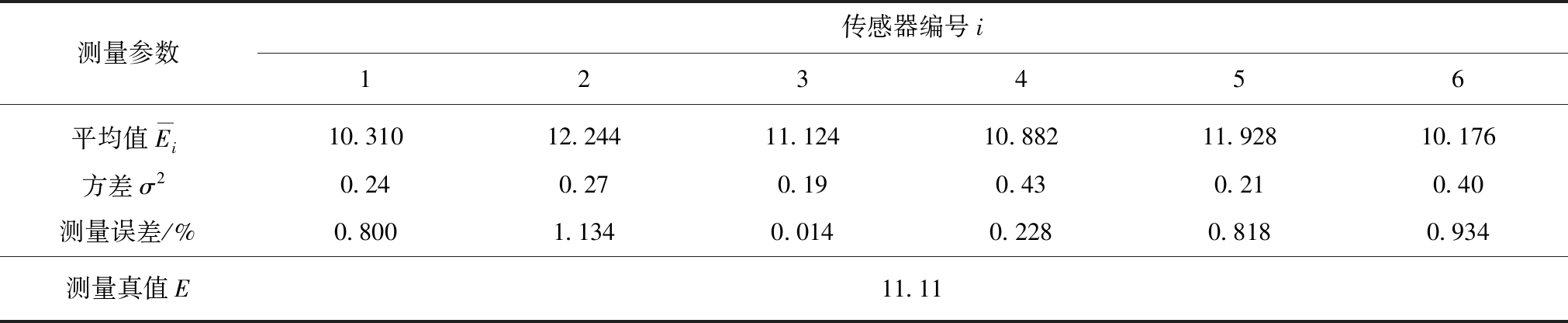
测量参数传感器编号i123456平均值Ei10.310 12.244 11.12410.882 11.92810.176方差σ20.24 0.27 0.190.430.210.40测量误差/%0.8001.1340.0140.2280.8180.934测量真值E11.11
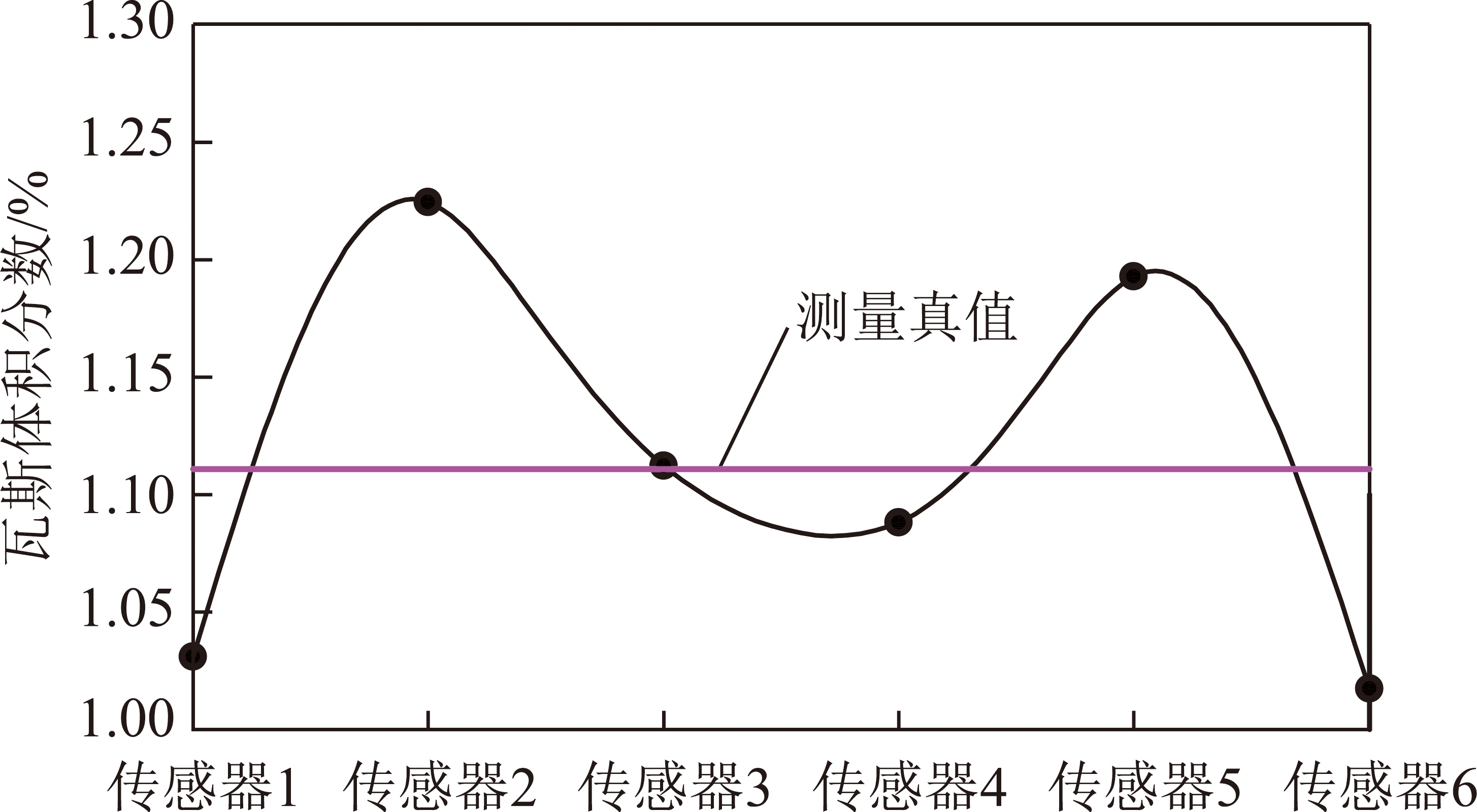
图3 监测数据分布曲线
Fig.3 Detection data distribution curve
3.3 数据融合处理过程
3.3.1 监测值影响因子的选择
如上所述，6只传感器工作于同一工作环境中，同时工作并以相同的频率监测所处位置的瓦斯体积分数值，故工作时所受环境影响和信息传送中所受信号干扰基本相同，传感器间的监测精度主要与监测设备的性能相关。在测量技术中，方差σ2是衡量监测设备性能的最佳参数，故本案例采用方差σ2作为传感器测量值的影响因子，分析监测设备性能与测量值间的相互关系。各传感器的测量值及其测量方差σ2见表2。
3.3.2 监测值与影响因子间关系式的计算
因最小二乘法具有数据处理过程中不需数据先验信息的优点，被广泛应用于对监测数据函数多项式的拟合中，并能取得理想的数据融合精度，故本案例采用最小二乘法拟合各传感器的测量值Ei及其影响因子xi之间的函数E(x)。表2为各传感器的测量值Ei及其影响因子xi(方差σ2)的参数值，为了求得测量值Ei及其影响因子xi之间的函数关系式E(x)，假设函数E(x)的数学表达式为
E(x)=a0+a1x+a2x2+…+anxn
(11)
从式(11)可以看出，函数E(x)的获取实质为多项式阶次n和系数ai的计算。
根据最小二乘法的定义，拟合的多项式阶次应小于数据样本的数量，故案例中所求的函数E(x)的阶次n<6。由于函数E(x)的拟合精度并不随着阶次n的增大而提高，故必须在0<n<6找到最佳阶次值，使得函数E(x)与测量真值之间的误差最小。应用Matlab软件中Polyfit函数，可以得到式(11)在不同阶次下的拟合总误差值，见表3。
表3 函数在不同阶次下的拟合总误差
Table 3 Total fitting error of function in different order
多项式阶次n12345E(x)总误差1.8071.9462.1143.344198.280
比较表3所示的不同阶次下拟合方程的测量误差可知:当拟合方程为二元一次方程时，各传感器的拟合值与测量真值之间的总误差最小。此时，E(x)函数的方程为
E(x)=a0+a1x
(12)
再次运用Matlab数学软件中的Polyfit函数，可以得出:a0=12.158,a1=-3.611 4。
这样即可得出基于最小二乘法的监测数据Ei与影响因子xi间的函数关系式为
E(x)=-3.611 4x+12.158
(13)
3.3.3 基于分数阶微分算子的监测数据融合模型
Grunwald-Letnikov定义下基于分数阶微分算子的煤矿井下瓦斯浓度监测信息的数据融合算法模型如式(9)所示，如想得到详细的数学模型，首先要确定式(9)中的阶次v和步长h的取值。
(1)阶次v的选择。
从图1所示的不同阶次v时分数阶微分算子的特性可以看出:在低频部分，当微分阶次0<v<1时，分数阶微分算子与整数阶算子相比具有一定的增强作用，而且随着阶次的降低，增强效果越明显，具有对信号的低频率成分非线性保留的作用。为了节约篇幅，本案例取[0,1]的中间值v=0.5，探讨分数阶微分算子对监测数据的融合处理效果。
(2)步长h的取值。
根据分数阶微积分的 Grunwald-Letnikov定义，可知步长h取值越小，计算的结果越精确，但是也会带来计算工作量增大的难题。因此，步长h的取值应综合考虑计算精度和速度两方面因素。本案例中，监测数据影响因子x的取值范围为[0.19，0.43]，故可将步长h取值0.01，这样需要计算的步数i=24，可以同时满足计算精度和速度两方面的要求。
现将分数阶次v=0.5和步长h=0.01代入式(9)，可得本案例中监测数据的融合算法模型:
(14)
3.4 监测数据融合结果
结合式(13)可以得出每一步E(x-ih)的数值，将计算结果代入式(14)，即可得到各传感器测量值E(xi)关于其影响因子xi(方差σ2)的0.5阶微分融合处理结果E0.5(xi)，见表4。
从表4所示最终融合结果可以看出:① 经过0.5阶分数阶微分算子融合处理后，煤矿井下监测点瓦斯浓度监测值有所提高，测量值经0.5阶微分算子融合处理后的测量平均值
为11.736，与测量真值E=11.11相比，数值提高了5.63%。② 各传感器间的测量误差大幅减小，使得原有的数据间离散性大幅下降，从图4所示的融合后监测数据分布曲线可以看出:经过0.5阶分数阶微分算子融合处理后，煤矿工作面的瓦斯体积分数值随机的分布在平均值附近。
表4 各传感器测量数据的0.5阶微分融合值
Table 4 0.5-order differential fusion values of measured data from each sensor
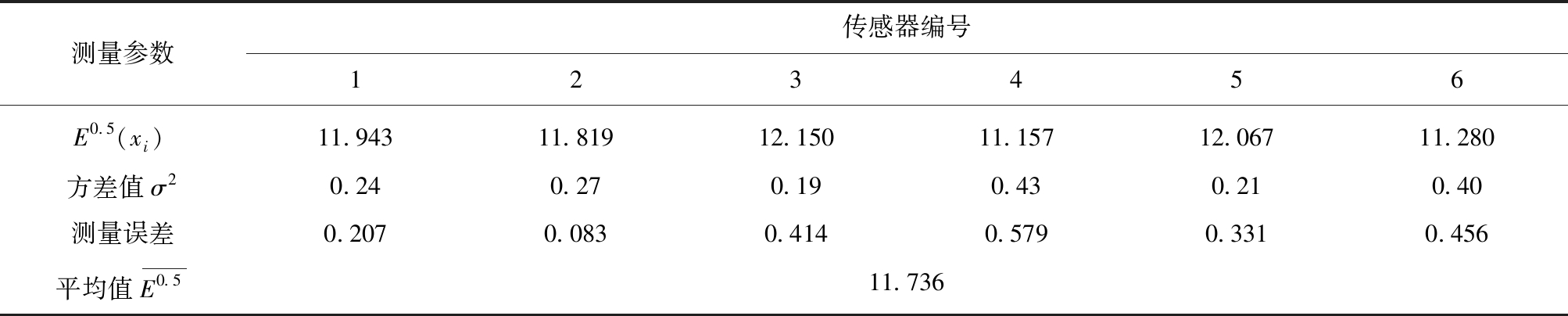
测量参数传感器编号123456E0.5(xi)11.94311.81912.15011.15712.06711.280方差值σ20.240.270.190.430.210.40测量误差0.2070.0830.4140.5790.3310.456平均值E0.511.736
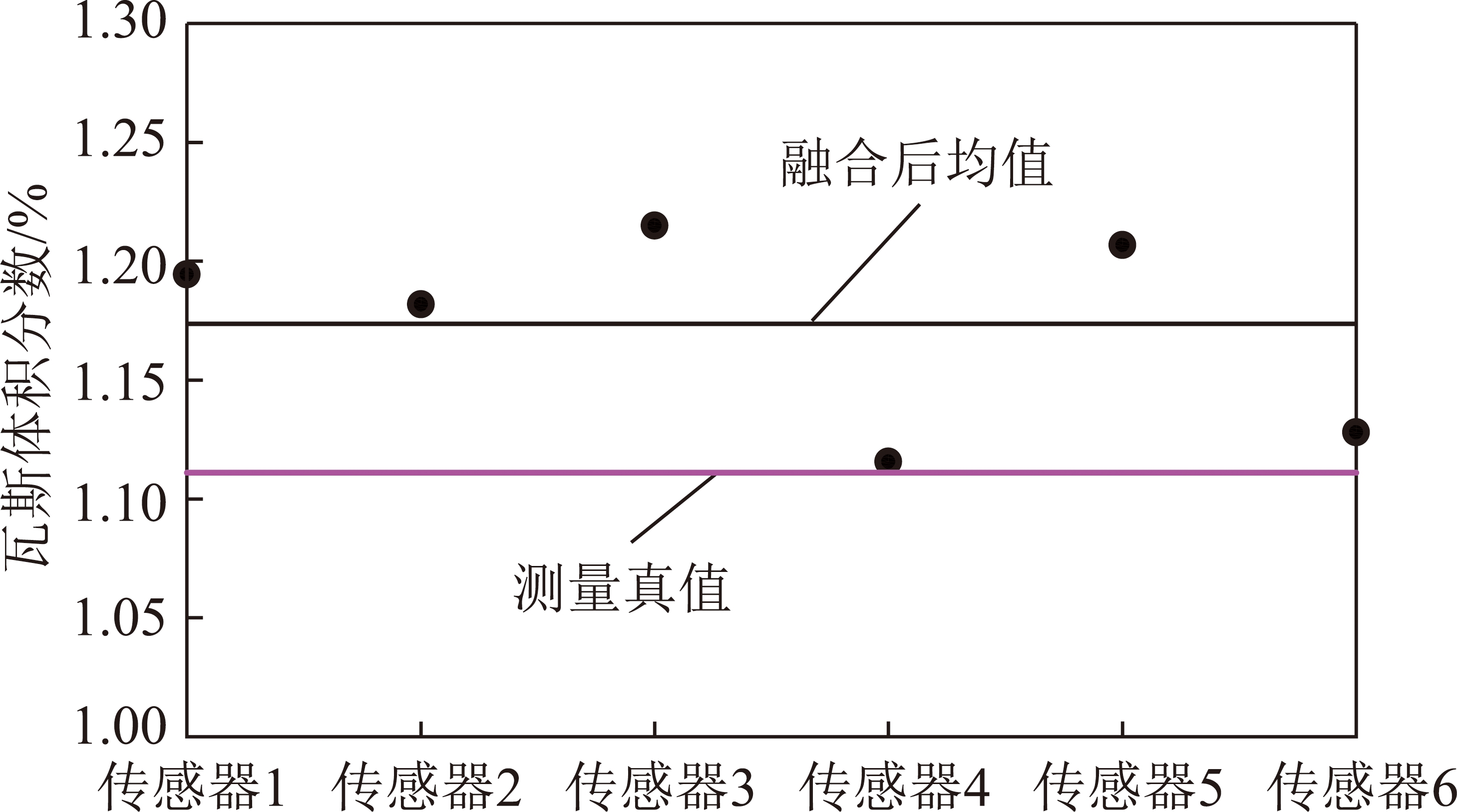
图4 0.5阶微分算子融合后监测数据分布曲线
Fig.4 Distribution curve of the detection data fused by 0.5- order differential operators
3.5 融合结果分析
表4所示数据是表2中各传感器监测数据经最小二乘法拟合后，应用0.5阶微分算子融合处理的结果。由式(13)可算得各传感器监测结果经最小二乘法拟合后的平均值为9.782，但经过0.5阶微分算子融合处理后的平均值达到11.736，数值提升了近20%。为便于比较分数阶微分算子与其他算法的优缺点，现将表4中各传感器的融合结果E0.5(xi)除去增强系数，可得出在平均值E=11.11时本文所用算法得到的最终融合值间的标准差为0.13，大幅小于卡尔曼滤波算法的标准差0.27和最小二乘法的标准差0.59，具有较好的融合处理精度。
4 结 论
(1)煤矿工作面的环境恶劣，导致物联网下煤矿生产信息监测系统采集到的生产信息难免存在测量误差大和信号失真等技术难题。煤矿生产信息监测硬件设施质量的大幅提升为以上难题的解决提供了可能，但庞大的煤矿生产信息采集系统硬件设施的更新将是一项耗资巨大的工程。本文综合考虑成本和技术等多重因素后，将分数阶微分滤波算法应用于物联网下煤矿生产信息数据的融合处理之中，通过监测数据分数阶微分融合算法来提高信息采集子系统的监测精度和工作可靠性。
(2)建立了基于分数阶微分算子的煤矿监测数据融合处理模型，通过对淮南某煤矿井下采空区瓦斯浓度监测数据的融合处理，验证了分数阶微分算子可以有效融合去数据采集过程中各种因素带来的测量误差，具有较高的多传感器监测数据融合精度，实现煤矿安全生产管理决策科学性和准确性的大幅提升，具有重要的实用价值。
[1] 武珍珍.数据挖掘在煤矿瓦斯检测系统中的研究[J].煤炭技术，2017,36(7):258-260.
WU Zhenzhen.Research on data mining in coal mine gas monitoring system[J].Coal Technology,2017,36(7):258-260.
[2] 殷大发.煤矿安全监控系统监测点数据异常识别技术研究[J].矿山机械，2013，41(4):120-123.
YING Dafa.Study on technology of identifying data abnormality of monitoring points in colliery safety monitoring system[J].Mining & Processing Equipment,2013，41(4):120-123.
[3] 王毅然.两级数据融合算法在没鲁昂粉尘监测中的应用研究[D].太原:太原理工大学，2017.
WANG Yiran.Application research of two-stage date fusion algorithm in coal mine dust monitoring[D].Taiyuan:Taiyuan University of Technology,2017.
[4] 冀少军.基于煤矿环境监测的多传感器数据融合算法研究[J].煤矿机械，2016,37(2):157-159.
JI Shaojun.Research on multi-sensor data fusion algorithm based on coal mine environment monitoring[J].Coal Mine Machinery,2016,37(2):120-123.
[5] 李海艳,李维嘉,黄运保.基于卡尔曼滤波的多传感器测量数据融合[J].武汉大学学报:工学版,2011(4):521-525.
LI Haiyan,LI Weijia,HUANG Yunbao.Multi-sensor measured data fusion based on Kalman filtering[J].Engineering Journal of Wuhan University,2011(4):521-525.
[6] 璩晶磊,李少波,张成龙.基于模糊证据理论的多传感器数据融合算法[J].仪表技术与传感器,2017(10):118-122.
QU Jinglei,LI Shaobo,ZHANG Chenglong.Multi-sensor data fusion algorithm based on fuzzy evidence theory[J].Instrument Technique and Sensor,2017(10):118-122.
[7] 张品,董为浩,高大冬.一种优化的贝叶斯估计多传感器数据融合方法[J].传感技术学报,2014,27(5):643-648.
ZHANG Pin,DONG Weihao,GAO Dadong.An optimal method of data fusion for multi-sensors based on Bayesian estimation[J].Chinese Journal of Sensors and Actuators,2014,27(5):643-648.
[8] 左延红,程桦,张克仁.基于分数阶偏微分的离散制造系统检测数据融合算法[J].计算机集成制造系统,2015,21(12):3256-3262.
ZUO Yanhong,CHENG Hua,ZHANG Keren.Fusion algorithm of discrete manufacturing system detection data based on fractional partial differential[J].Computer Integrated Manufacturing Systems,2015,21(12):3256-3262.
[9] PODLUBNY I.Fractional differential equations,mathematics in Science and Engineering[M].New York:Academic Press,1999.
[10] DARLING R,NEWMAN J.On the short behavior of porous intercalation electrodes[J].Journal of the Electrochemical Society,1997,144(9):3057-3063.
[11] FELLAH M,FELLAH Z E A,DEPOLLIER C.Transient wave propagation in inhomogeneous porous materials:Application of fractional derivatives[J].Signal Processing,2006,86(10):2658-2667.
[12] MEERSCHAERT M M,MORTENSEN J,WHEATCRAFT S W.Fractional vector calculus for fractional advection-dispersion[J].Physicaa,2006,367:181-190.
[13] TENREIRO Machado J A,ISABEL S Jesus,ALEXANDRA Galhano,et al.Fractional order electro-magnetic[J].Signal Processing,2006,86(10):2637-2644.
[14] DAVIS G B,KOHANDEL M,SIVALOGANATHAN S,et al.The constitutive properties of the brain paraenchyma Part 2.Fractional derivative approach[J].Medical Engineering & Physics,2006,28(5):455-459.
[15] SIEROCIUK D.Fractional Kalman Filter algorithm for states,parameters and order of fractional systeme stimation[J].International Journal of Applied Mathematics and Computer Science,2006,16(1):1-14.
[16] 张意,蒲亦非,周激流.分数阶微分掩模及其滤波器的构造[J].华南理工大学学报(自然科学版),2011，39(7):95-101.
ZHANG Yi,PU Yifei,ZHOU Jiliu.Construction of fractional derivation masks and corresponding filter[J].Journal of South China University of Technology(Natural Science Edition),2011,39(7):95-101.
[17] 廖一鹏，王卫星，付华栋，等.结合分数阶微分的浮选泡沫图像NSCT多尺度增强[J].华南理工大学学报(自然科学版)，2018,46(3):92-102.
LIAO Yipeng,WANG Weixing,FU Huadong,et al.Flotation foam image NSCT multi-scale enhancement with fractional differential[J].Journal of South China University of Technology(Natural Science),2018,46(3):92-102.
[18] TRELEA I C.The particle swarm optimization algorithm:Convergence analysis and parameter selection[J].Information Processing Letters,2003,85(6):317-325.
