吴元
人工土冻结法(以下简称“冻结法”)由于基本不受支护范围和支护深度的限制，以及能有效防止涌水以及城市挖掘、钻凿施工中相邻土体的变形而受到越来越多的重视[1]，并广泛应用于矿井、隧道、基坑工程、盾构进出洞、联络通道等多种工程[1-2]。
由于冻结法中冻土的物理力学性质对温度敏感性很高，其在冻结、开挖过程中都有可能发生险情或事故。例如，安徽某煤矿主副井因冻结深度未达到要求而导致淹井[3]，俄罗斯圣彼得堡地铁因过大的地下水流速和含盐地层导致冻土帷幕未封闭而引发的隧道突涌水[4]，以及上海某临江地铁的联络通道施工中因多种因素导致承压水突涌的事故[5]。
对诸多事故的原因调查结果表明，冻结工程的安全性与地下水和冻土的相互作用有很大关系。关于地下水对冻土帷幕在形成过程中的影响的研究已有相当丰富的成果[6-8]，而对于冻结工程灾害发生时，地下水对冻土的削弱、侵蚀作用的研究较少[3]。笔者对冻土帷幕中的渗水孔隙等灾害源在地下水的侵蚀作用下逐渐扩展的过程进行研究，在一定假设条件下对该物理过程进行简化，建立了相应的相变传热模型并进行了求解和验证。研究的结果对冻结工程事故的灾变机理和灾害控制有一定的理论意义和工程指导价值。
由于移动边界(冻结锋面)带来的非线性，笔者所研究的圆柱坐标系下基于对流换热边界条件(第三类边界条件)的固体相变问题目前并无精确解析解[9]。因此，笔者采用由GOODMAN提出的热平衡积分方法(HBIM)[10-15]，根据LARDNER等的建议[16]，采用对数形式温度分布假设对该问题进行理论求解，并采用结合了坐标变换的有限差分方法进行数值验证。笔者建立的相变传热模型具有一般性，对该相变传热问题的研究成果可应用于竖井冻结壁出水、多年冻土隧道渗漏水、天然冻土河岸冲刷等问题的研究。
本文研究的物理过程如图1(a)所示，设想冻土内有一孔隙，当地下水流经该孔时，水流与冻土之间形成对流换热边界Ω，孔洞四周冻土升温至融点后融化，融土被地下水带走，于是水流与冻土的作用边界逐渐向外扩展，即孔洞半径不断扩张。针对上述物理过程，本文采用如下假设来建立传热模型:
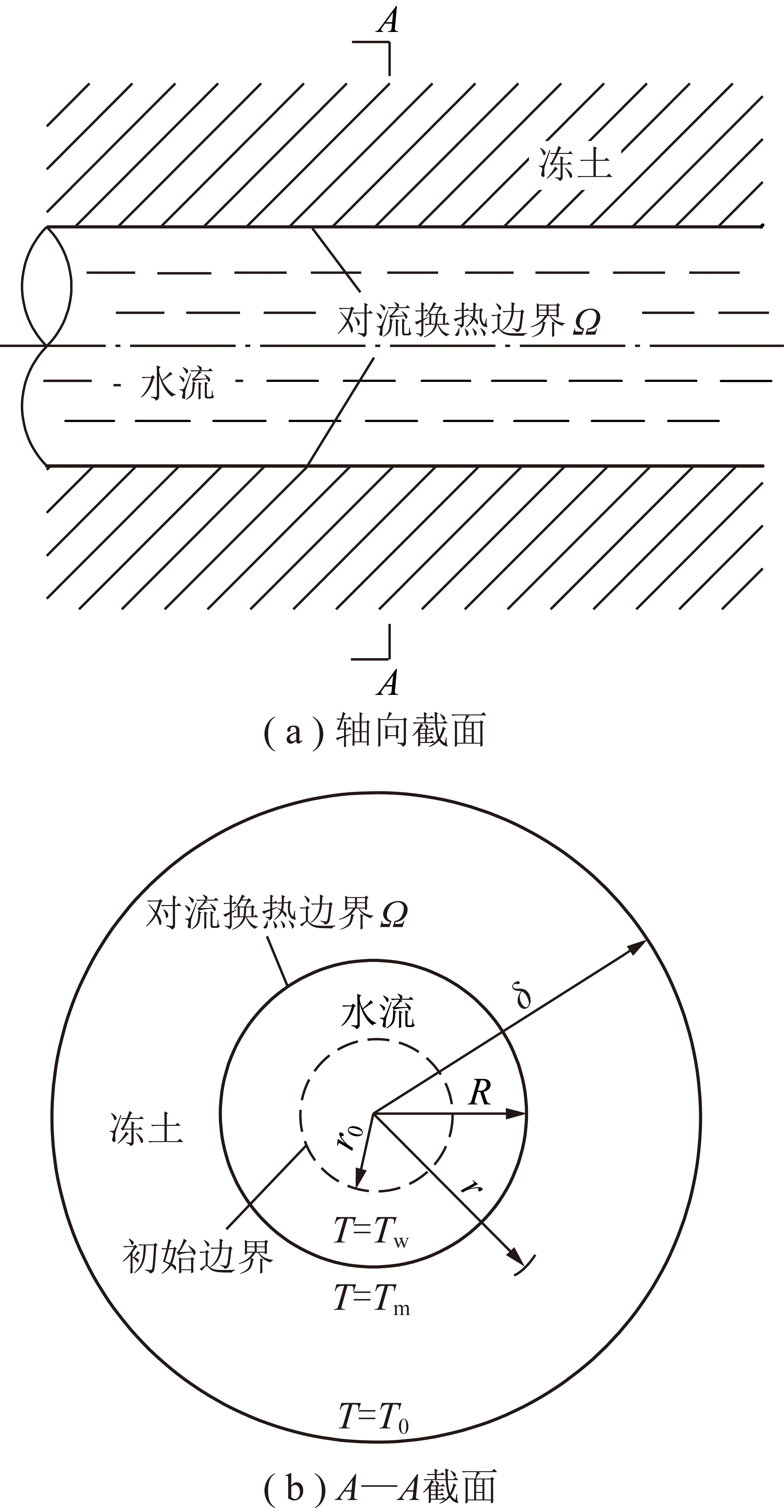
图1 计算模型示意
Fig.1 Schematic diagram of the phase change problem
(1)内孔隙假定为一半径为R的圆孔，且孔洞轴向与冻结壁轴向(冻结孔轴向)垂直，孔洞距离冻土边界较远，不考虑边界热流对孔洞扩展的影响。
(2)在孔洞周围的冻土视为均匀温度分布，即不考虑冻土温度梯度的影响。
(3)在孔径逐渐扩大的过程中，水温、边界上的对流换热系数均假定为常数。
(4)融化后的土颗粒能够立即被水流带走，即将水流侵蚀形成的“孔洞边界”与“冻土融化相变边界”视为重合。
在上述假定下，该问题可转化为圆柱坐标系下一维径向热传导问题，边界Ω的移动规律即是圆孔半径R随时间的变化规律。Ω既是水流与冻土的换热边界也是冻土的相变边界，其随时间的扩展情况是本文研究的重点。
具体的计算参数如图1(b)所示，为图1(a)截面A-A示意图，设初始孔径为r0，侵蚀移动相变边界Ω的位置坐标为R，热平衡积分法中的热层厚度为δ。冻土的初始时刻温度分布均匀，其值为T0，冻土融化温度为Tm，水流温度为Tw。其中，热层厚度δ的定义为:从实际角度出发，认为超过某一厚度就不存在热流，则将此厚度定义为热层厚度。因此，超过热层厚度δ以外，初始的温度分布就不再受影响。
设所研究对象的温度分布函数为T(r,t)，其中r为空间坐标，t为时间。则该热传导问题的控制方程及基于上述热层定义的定解条件如下:
(1)
当r=R(t)时，T=Tm
(2)
当r=δ(t)时，T=T0
(3)
当r=δ(t)时，
(4)
当t=0时，T=T0
(5)
式中，α为导温系数，满足α=k/(ρc)，其中ρ为密度;k为导热系数;c为比热容。
相变界面处能量平衡方程为
(6)
式中，l为单位物质的相变潜热;h为固液间的对流换热系数。
根据LARDNER等的建议[16]，在柱坐标系下应用热积分平衡方法时，常规的多项式形式的温度分布假设已经不适用，推荐采用对数分布的形式。这里结合边界条件，假设冻土内温度分布函数T(r,t)满足:
(7)
可验证，式(7)已满足定解条件式(2)～(5)。用算子
rdr对式(1)两边进行积分，并利用莱布尼兹积分法则(Leibniz Integral Rule)和模型的边界条件式(4)得到热平衡积分方程:
(8)
式中，ω定义为:ω=rTdr。
将式(7)代入式(6),(8)，得到
(9)
(10)
(11)
为了后续讨论方便，采用了如下无量纲参数:
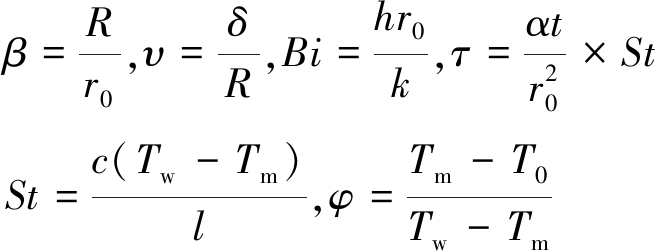
(12)
经过上述过程，非线性偏微分方程转化为常微分方程组(式(9)～(11))。用传统的四阶荣格-库塔(Runge-Kutta)方法即可求解该常微分方程组。
相变边界随时间由内向外移动，求解区域也随之变化。本文参考SPARROW等[17]提到的方法，采用坐标变换方法将求解边界固定。为此，引入如下变量代换:
(13)
则控制方程式(1)及定解条件变为
(14)
当η=0时，θ=0
当 η=1时，θ=φ
当 η=1时，
当 τ=0时，θ=φ
为方便,定义Δ为:Δ=(δ-R)/r0。
相变界面的能量平衡方程式(6)变为
(15)
为了求解上述偏微分方程，需要定义无量纲热层厚度相关的量Δ和无量纲边界位置β之间的关系。令Δ=Cβ，其中C取一个较大的值，以使热层厚度足够大从而不影响数值结果的准确性。
将变量代换后的控制方程式(14)写成:
(16)
其中:
ρ=C2×St×β2，
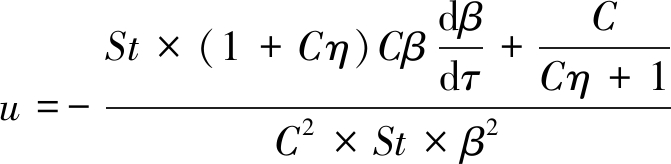
则原来的热传导方程经过变量代换变成了对流-扩散型方程的形式，见式(16)[18]。对于该方程，根据控制容积法，采用乘方定律格式[17]进行离散。如图2所示为结点P及周边的结点W,E组成的典型结点组。
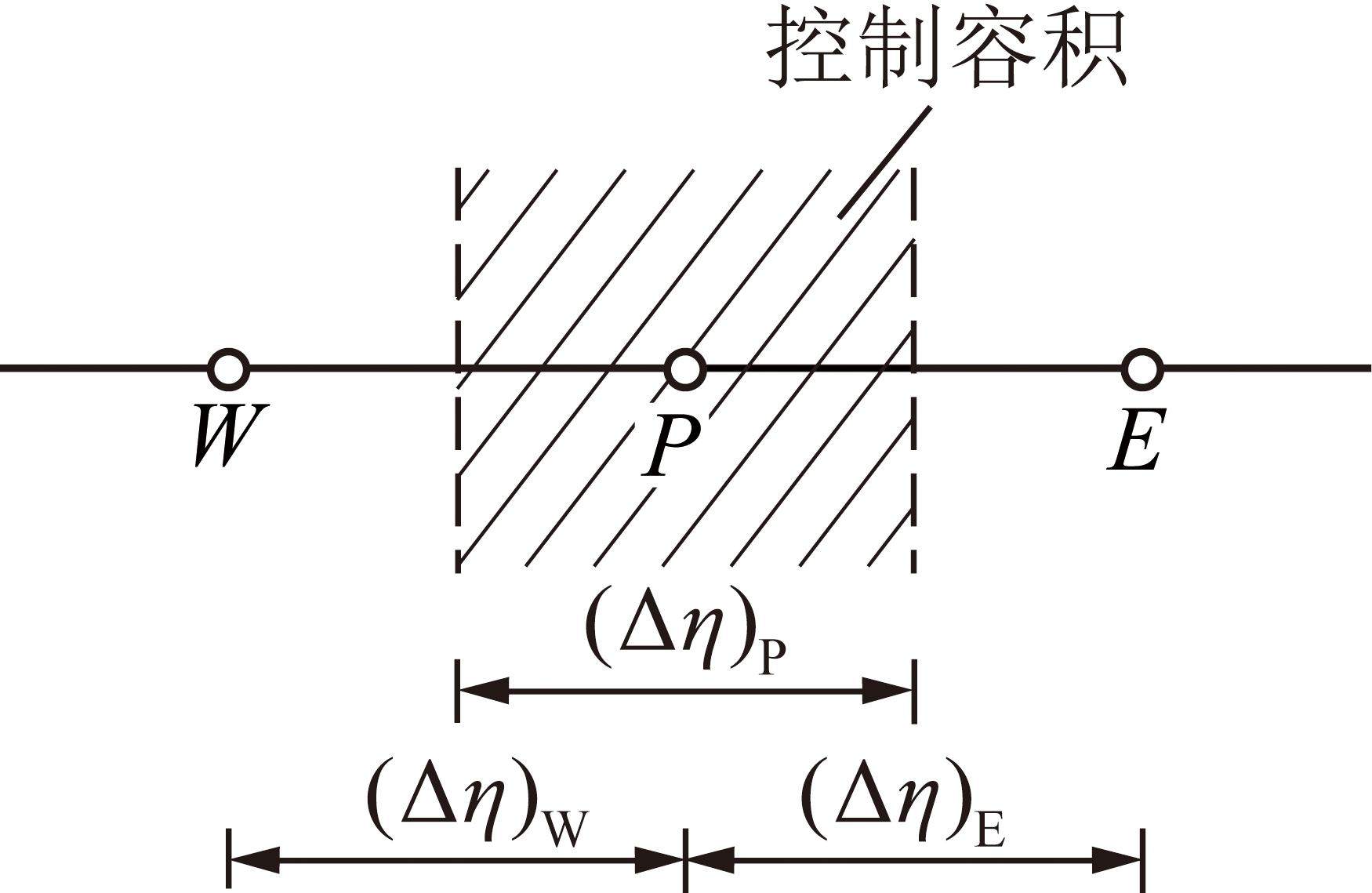
图2 典型计算节点组示意
Fig.2 Schematic diagram of a representative point group
在P点上，方程(14)离散为
(17)
式中，上标“0”和“1”为τ0时刻及τ0+Δτ时刻的值;下标P，W和E为对应节点处的值。其中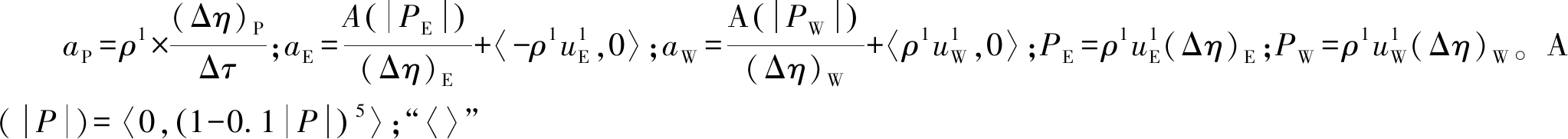
表示取括号内所有量中最大值。
由相变界面的能量平衡方程(15)可得
则关于相变界面的能量平衡方程差分格式为
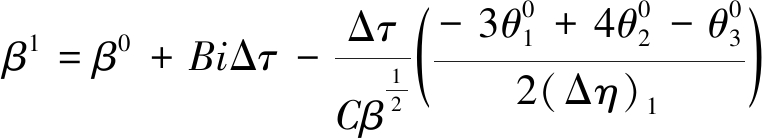
(18)
式中，
和
分别为相变界面边界点以及其旁边两点处在τ0时刻的θ值;
为β在τ0+Δτ/2时刻的值，可由β0参照上式直接得到，目的是保证相变界面的能量平衡方程的差分格式和主控制方程的差分格式具有相同阶数的精度。
至此，在假定温度初值后，相变界面的能量方程可通过式(18)显式求解，其求出的结果可以作为主控制离散方程(17)的参数，继而通过方程(17)得到的系数矩阵可通过无需迭代的三角矩阵算法(TDMA)直接求解。
现根据上海市某隧道工程的地质勘测报告求解一具体算例，冻土的热物理性质及温度边界条件等各参数取值情况见表1。
表1 算例参数取值
Table 1 Parameter values of the example
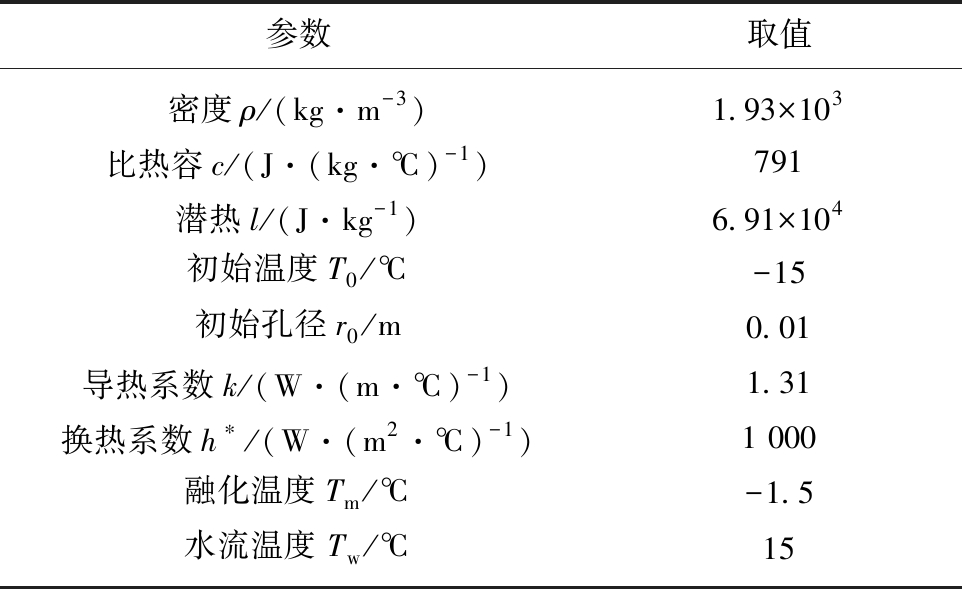
参数取值密度ρ/(kg·m-3)1.93×103比热容c/(J·(kg·℃)-1)791潜热l/(J·kg-1)6.91×104初始温度T0/℃-15初始孔径r0/m0.01导热系数k/(W·(m·℃)-1)1.31换热系数h∗/(W·(m2·℃)-1)1 000融化温度Tm/℃-1.5水流温度 Tw/℃15
注：*该值系根据对流换热的Gnielinski实验关联式计算后取整得到[19]。
根据表1，St=c(Tw-Tm)/l=0.189，Bi=hr0/k=7.63，φ=(Tm-T0)/(Tw-Tm)=0.818。
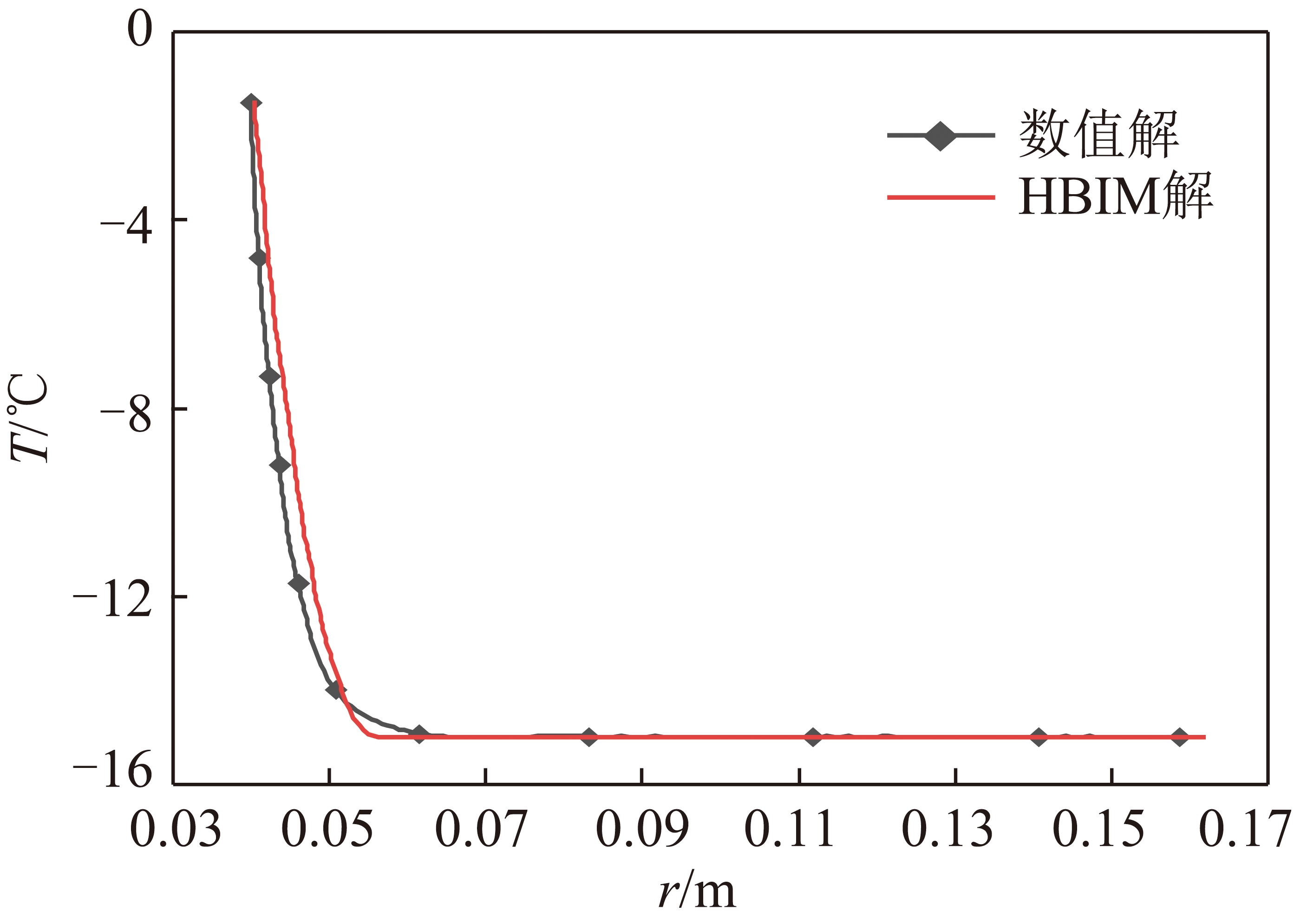
图3 t=5 min时温度分布情况
Fig.3 Temperature distribution at t=5 min
分别采用热平衡积分方法和数值方法求解上述算例。时间t=5 min时冻土的温度T随r分布情况以及侵蚀相变边界R随时间t的变化关系分别如图3,4所示。由图3可知，t=5 min时相变边界移动至r=0.04 m左右的位置，相变边界附近的温度梯度较大，说明此处热交换剧烈。而在r≥0.07 m的范围，温度基本维持在初始温度，温度梯度基本为0，说明热量还未传导至该区域。由图4可知，相变边界R随时间近似线性变化，变化速率约为0.106 mm/s。
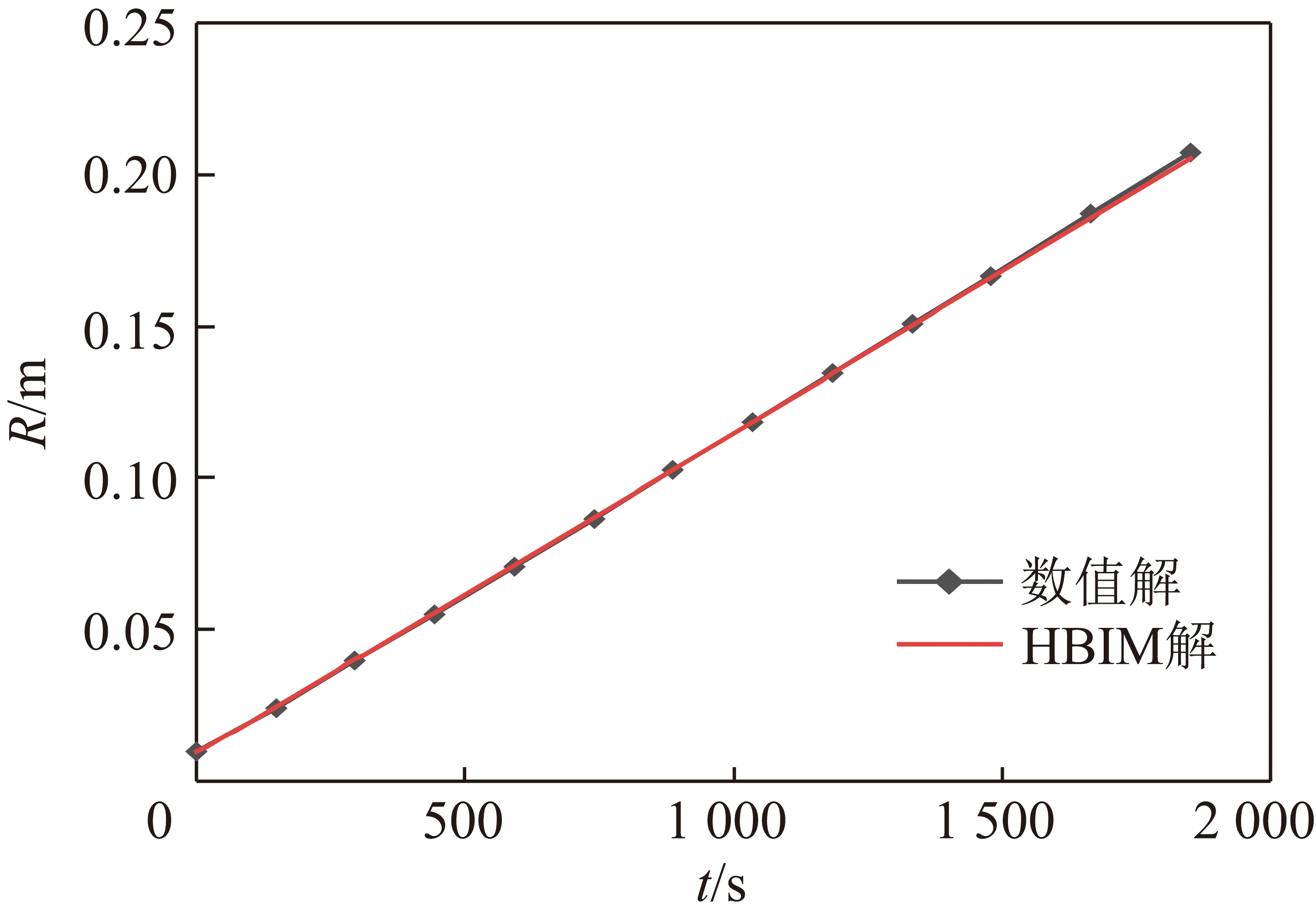
图4 侵蚀相变边界R随时间t变化情况
Fig.4 Phase change position R vs time t
而且从图3,4可以看到，数值解与热平衡积分解结果吻合的较好，尤其是移动界面R的数值解与解析解偏差很小，计算结果表明二者最大偏差不超过0.1%。说明本文采用的热平衡积分求解方法能够适用于柱坐标系下的对流相变问题的求解，尤其是对于相变边界位置R，该方法能够得到令人满意的结果。为了保证结果的正确性，在后续的分析中，均把数值解与热平衡积分解包括在内。
由上述求解过程可知，影响相变界面位置β随时间变化规律的因素有:史蒂芬数St、毕渥数Bi、以及过冷系数φ。根据冻土及水的热物理性质及实际工程温度条件，将上述3个影响因素的代表性取值及组合列于表2。
表2 影响因素的代表性取值及组合
Table 2 Representative values of St,Bi and φ
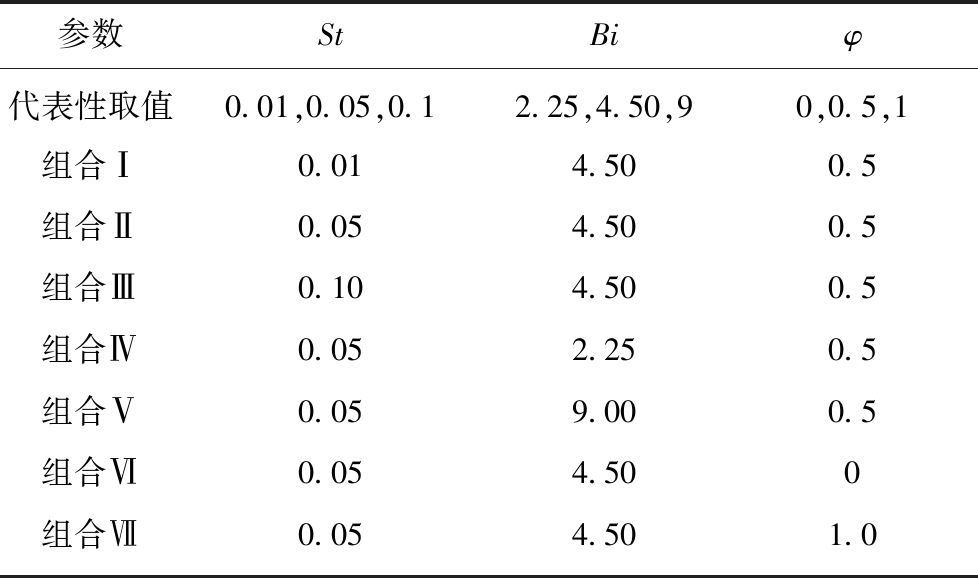
参数StBiφ代表性取值0.01,0.05,0.12.25,4.50,90,0.5,1组合Ⅰ0.014.500.5组合Ⅱ0.054.500.5组合Ⅲ0.104.500.5组合Ⅳ0.052.250.5组合Ⅴ0.059.000.5组合Ⅵ0.054.500组合Ⅶ0.054.501.0
为了消除无量纲时间参数τ中史蒂芬数St的影响，取傅里叶数Fo为后续分析的无量纲时间参数:
图5～7分别反映了St,Bi,φ变化时对侵蚀相变速率的影响。
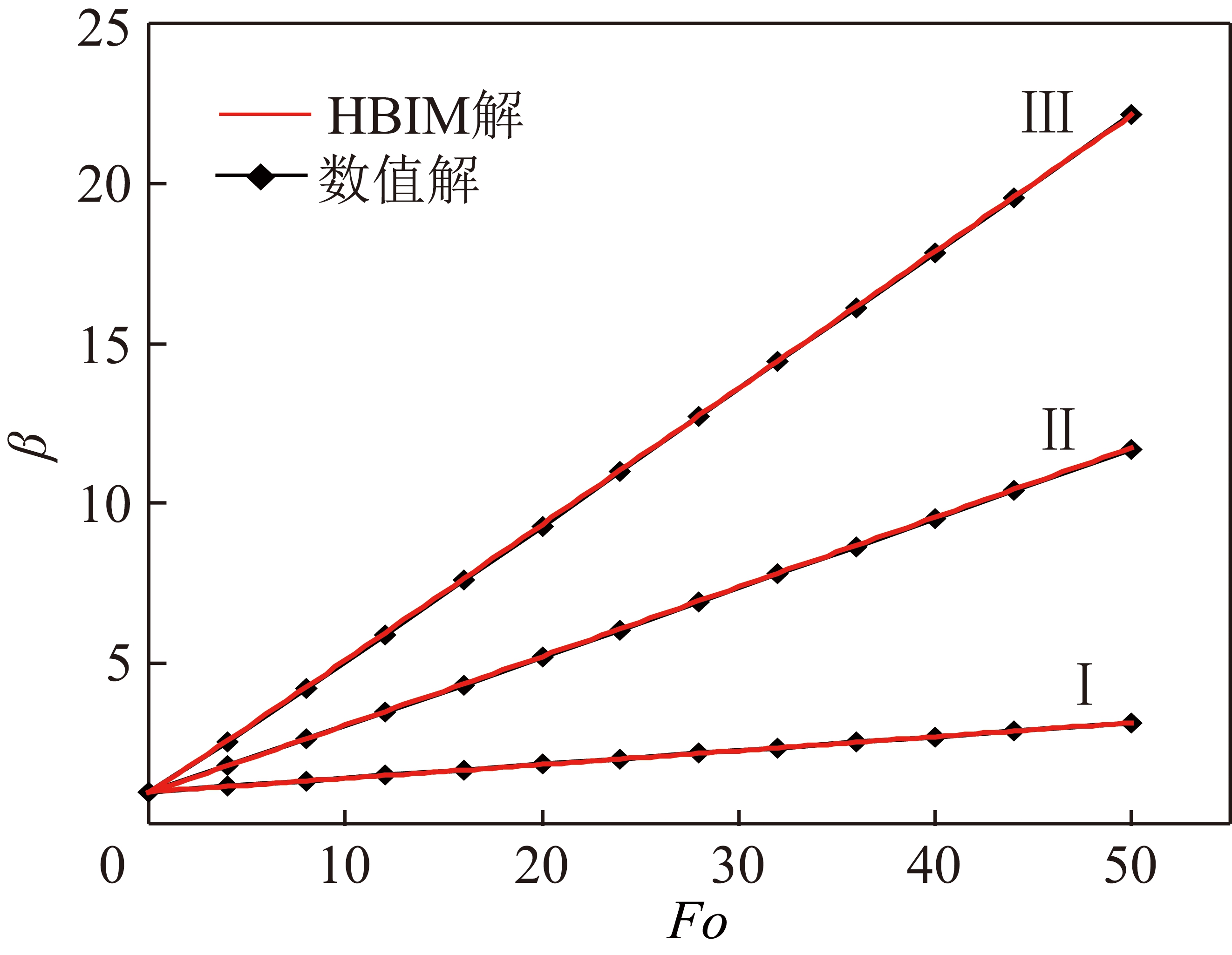
图5 不同St条件下侵蚀相变位置β随Fo变化
Fig.5 Phase change position β vs Fo under the condition of different St
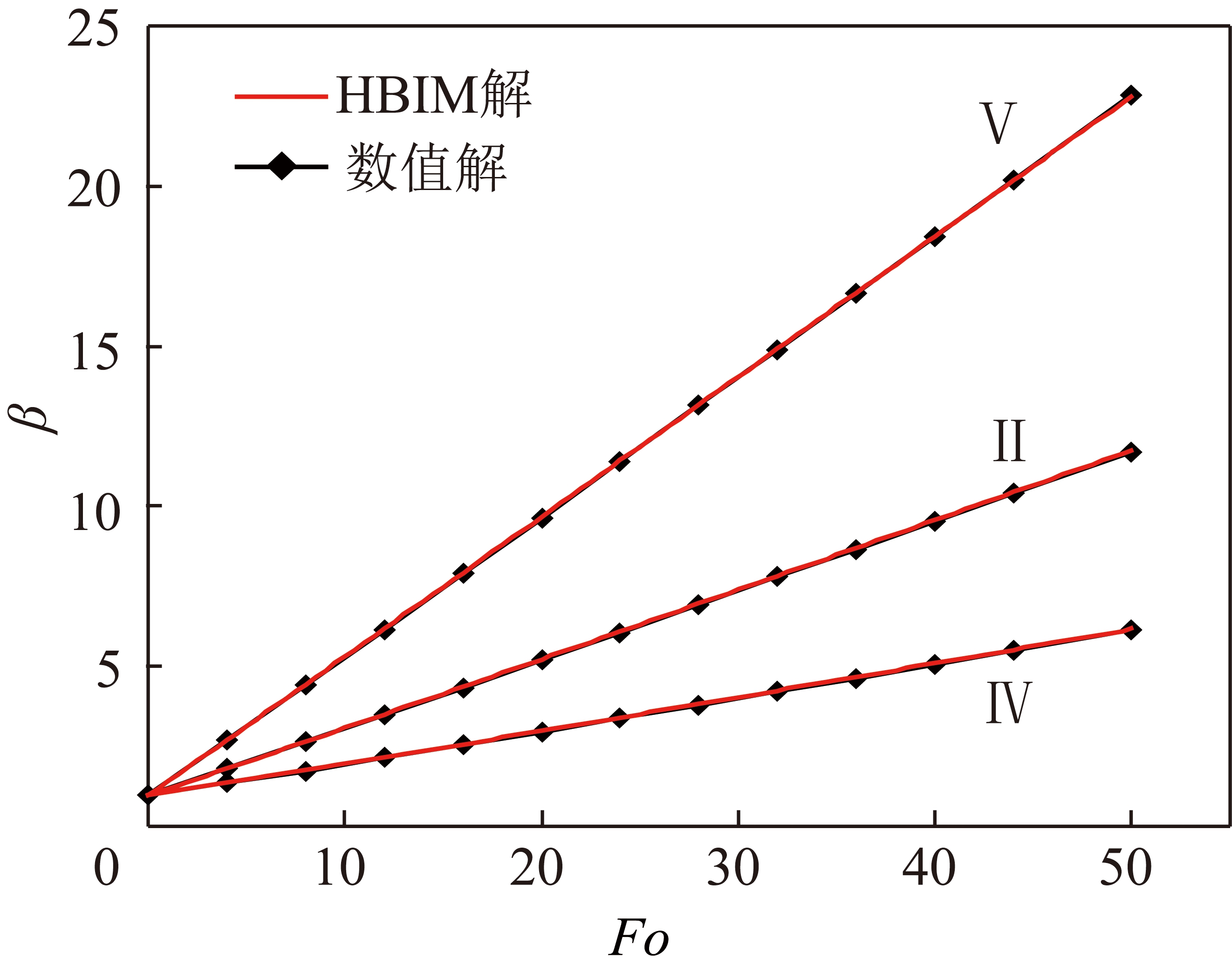
图6 不同Bi条件下侵蚀相变位置β随Fo变化
Fig.6 Phase change position β vs Fo under the condition of different Bi
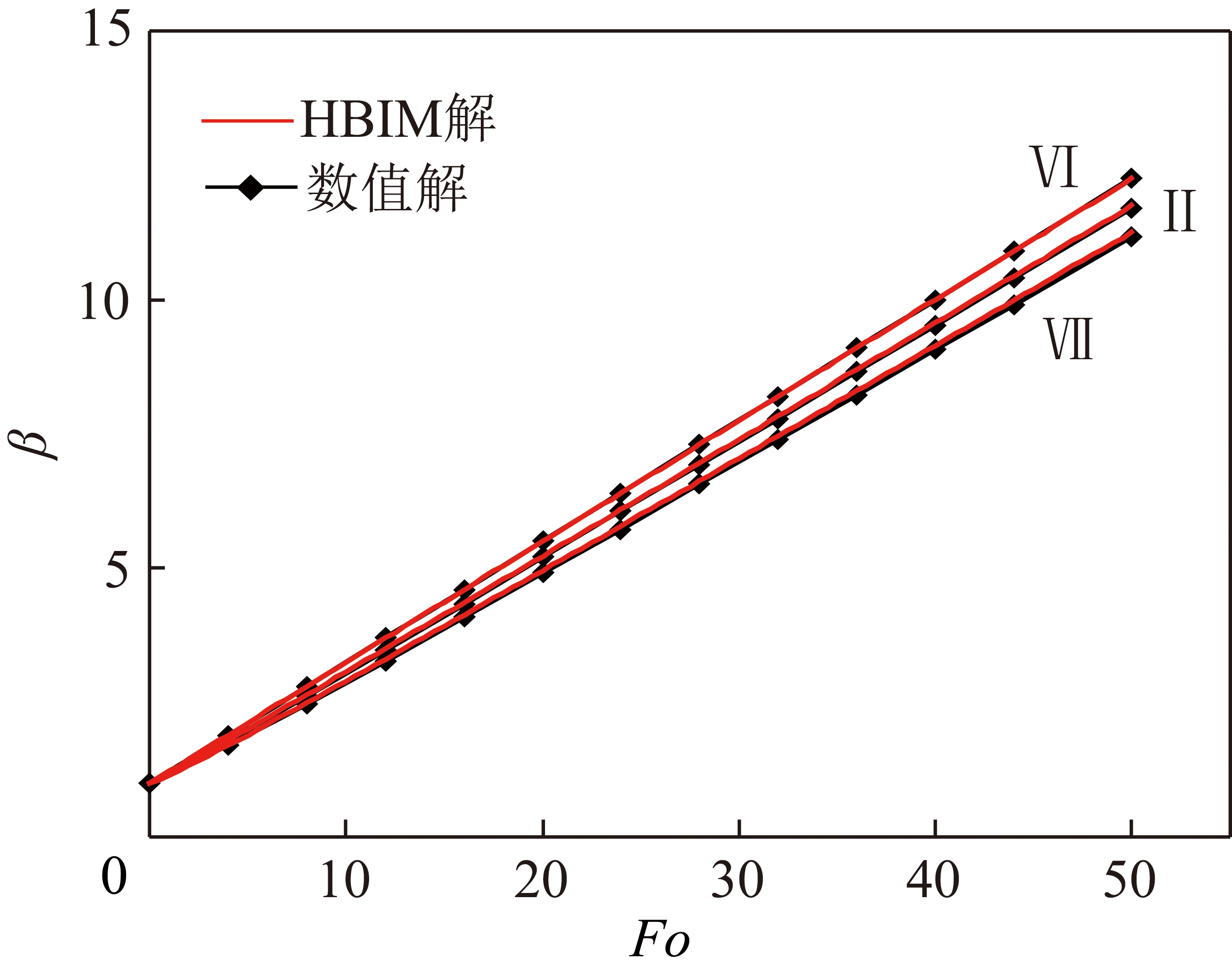
图7 不同φ条件下侵蚀相变位置β随Fo变化
Fig.7 Phase change position β vs Fo under the condition of different φ
其中，图5表明在其他参数不变时，随着史蒂芬数St的增加，侵蚀相变速率明显增大。由St计算公式:St=c(Tw-Tm)/l，可知在冻土的热物性参数c,l以及Tm一定的条件下，St主要取决于水流温度大小。St越大，意味着Tw值越大，则水流与冻土的换热量越大，即相变潜热交换量越大，所以侵蚀相变速率越大。以该图中的数据为例，当Tw由5 ℃(对应St约为0.05)上升一倍至10 ℃(对应St约为0.1)时，侵蚀相变速率也增加了1倍。
图6则表明在其他参数不变时，随着毕渥数Bi的增加，侵蚀相变速率也明显增大。由Bi计算公式:Bi=hr0/k，可知在冻土的热物性参数k以及初始孔径一定的条件下，Bi主要取决于对流换热系数h的大小。h值越大，意味着Bi越大，则水流与冻土的换热量越大，即相变潜热交换量越大，所以侵蚀相变速率越大。以该图中的数据为例，当h由600 W/(m2·℃)(对应Bi约为4.5)上升1倍至1 200 W/(m2·℃)(对应Bi约为9)时，相变速率也增加了1倍左右。
图7表明在其他参数不变时，随着过冷系数φ的增加，侵蚀相变速率相应减小。由φ计算公式:φ=(Tm-T0)/(Tw-Tm)，可知在冻土的融化温度Tm以及水流温度一定的条件下，φ主要取决于冻土初始温度T0的大小。T0值越大，意味着φ越小，冻土初始温度越低，则水流与冻土的换热量中显热量占比增加，相应地相变潜热量占比降低，所以侵蚀相变速率减小。以该图中的数据为例，当T0由-7.5 ℃(对应φ约为0.5)下降1倍至-15 ℃(对应φ约为1)时，相变速率减小了5%左右。
由图5～7可知，不管在哪种情况下，侵蚀相变位置随时间均呈现出近似线性变化规律。但St,Bi,φ三者变化时对侵蚀相变速率的影响程度不同:在其他参数不变的条件下，St,Bi增大1倍时，侵蚀相变速率均增加1倍左右，而φ增加一倍时，侵蚀相变速率仅减小了5%。所以，在实际工程中，降低冻土的平均温度是能够减缓侵蚀相变速率的，但作用十分有限;相反，降低水流温度或者减缓水流的流速等措施则能够有效减缓水流侵蚀速率。
由于在实际工程中，随着孔洞半径R逐渐增大，水流的流速、水温以及边界上的对流换热系数也会随之变化，因此在具体工程取值计算时需考虑这些因素的实际变化对求解结果的影响。对于地下水温度Tw，由于水流在穿过孔洞时会吸收周围冻土的冷量，当孔径较小，流速较慢时，水温低于正常情况下的地下水温度;而当孔径增大，流速加快时，水温会比较接近正常的地下水温，所以对Tw取值为地下水正常平均温度时，所估算的相变界面换热量比实际偏高，得到的侵蚀速率也偏高，对于工程来讲是偏于安全的。而对于对流换热系数h，当孔径较小时，流速较慢且孔内水流形式可能为层流，相应换热系数较小;当孔径较大时，流速加快，流动形式也更接近于湍流，相应换热系数较大，因此h取值计算时应考虑成湍流且对于流速应取一个较大值，这样得到的侵蚀速率会比实际偏高，对于工程来讲也是偏安全的。
此外，在建立计算模型时，本文认为融化后的土颗粒能够立即被水流带走(第1节假设(4))，该假设对于要求水流达到一定速度的同时，土颗粒间的黏结作用也要较小。在孔隙发展到一定程度后，这种假定对于颗粒间黏聚力较小的砂性土是较为合理的，但对于黏性土而言，颗粒未必会被立即带走。因此在定量参考本文的计算结果时，可将得到的相变侵蚀速率视为冻结工程灾害发生时孔隙发展速度的上限值。
(1)本文采用基于对数形式温度分布的热平衡积分方法(HBIM)求解第三类边界条件下圆孔相变问题是可行的，尤其对于相变边界位置R的求解，该方法能够得到令人满意的结果。
(2)在不同的控制参数情况下，侵蚀相变位置随时间均呈现出近似线性变化规律，在其他参数不变的条件下，St,Bi增大一倍时，侵蚀相变速率均增加一倍左右，而φ增加一倍时，侵蚀相变速率仅减小了5%。
(3)在实际工程中，降低冻土的平均温度是能够减缓侵蚀相变速率的，但作用十分有限;相反，降低水流温度或者减缓水流的流速等措施则能够有效减缓水流侵蚀速率。
(4)利用本文结果预测实际冻结工程灾变过程时，需考虑土性的不同以及地下水温度、对流换热系数等随孔径变化带来的影响，可将由本文方法得到的相变侵蚀速率视为冻结工程灾害发生时孔隙发展速度的上限值。
[1] 陈瑞杰，程国栋，李述训，等.人工地层冻结应用研究进展和展望[J].岩土工程学报，2000，22(1):43-47.
CHEN Ruijie，CHENG Guodong，LI Shuxun，et al.Development and prospect of research on application of artificial ground freezing[J].Chinese Journal of Geotechnical Engineering，2000，22(1):43-47.
[2] MA W.Review and prospect of the studies of ground freezing technology in China[J].Journal of Glaciology and Geocryology，2001，23(3):218-224.
[3] 李柱和.临江地铁冻结工程事故机理及修复技术研究[D].北京:中国矿业大学(北京)，2013:6-10.
LI Zhuhe.Research on the mechanics about accident of subway engineering with refrigeration construction technology and its repairing technology[D].Beijing:China University of Mining and Technology(Beijing)，2013:6-10.
[4] 胡向东，白楠，李鸿博.圣彼得堡地铁1号线区间隧道事故分析[J].隧道建设，2008，28(4):418-422.
HU Xiangdong，BAI Nan，LI Hongbo.Analysis on tunnel accident on Line 1 of Saint Petersburg Metro[J].Tunnel Construction，2008，28(4):418-422.
[5] 白云，汤竞.软土地下工程的风险管理[J].地下空间与工程学报，2006，2(1):21-27.
BAI Yun，TANG Jing.Risk management of for underground project in soft soils[J].Chinese Journal of Underground Space and Engineering，2006，2(1):21-27.
[6] 赖远明，吴紫汪，朱元林，等.寒区隧道温度场、渗流场和应力场耦合问题的非线性分析[J].岩土工程学报，1999，21(5):529-533.
LAI Yuanming，WU Ziwang，ZHU Yuanlin，et al.Nonlinear analysis of the coupling of temperature，seepage and stress fields of tunnels in cold region[J].Chinese Journal of Geotechnical Engineering，1999，21(5):529-533.
[7] 杨平，皮爱如.高流速地下水流地层冻结壁形成的研究[J].岩土工程学报，2001，23(2):167-171.
YANG Ping，PI Airu.Study on the effects of large groundwater flow velocity on the formation of frozen wall[J].Chinese Journal of Geotechnical Engineering，2001，23(2):167-171.
[8] 周晓敏，王梦恕，张绪忠.渗流作用下地层冻结壁形成的模型试验研究[J].煤炭学报，2005，30(2):196-201.
ZHOU Xiaomin，WANG Mengshu，ZHANG Xuzhong.Model test research on the formation of freezing wall in seepage ground[J].Journal of China Coal Society，2005，30(2):196-201.
[9] CARSLAW H S，JAEGER J C.Conduction of heat in solids[M].London:Clarendon Press，1986:1054-1057.
[10] GOODMAN T R.Application of integral methods to transient nonlinear heat transfer[J].Advances in Heat Transfer，1964(1):51-122.
[11] LUNARDINI V J，VAROTTA R.Approximate solution to neumann problem for soil systems[J].Journal of Energy Resources Technology，1981，103(1):76-81.
[12] 何绍杰.用热平衡积分法求瞬态温度场近似解[J].上海第二工业大学学报，1990(1):63-71.
HE Shaojie.Approximate solution for instantaneous temperature distribution by heat balance integration method[J].Journal of Shanghai Second Polytechnic University，1990(1):63-71.
[13] VENKATESHAN S P，RAO V R.Approximate solution of non-linear transient heat conduction in cylindrical geometry[J].Heat & Mass Transfer，1991，26(2):97-102.
[14] MYERS T G，MITCHELL S L，MUCHATIBAYA G，et al.A cubic heat balance integral method for one-dimensional melting of a finite thickness layer[J].International Journal of Heat & Mass Transfer，2007，50(25):5305-5317.
[15] 刘永杰，令锋.边界条件随时间变化Stefan问题的一种热平衡积分解法[J].内蒙古大学学报(自然科学版)，2010，41(6):625-631.
LIU Yongjie，LING Feng.A heat balance integral method for the Stefen problem with time-dependent boundary conditions[J].Journal of Inner Mongolia University(Natural Science Edition)，2010，41(6):625-631.
[16] LARDNER T J，POHLE F V.Application of the heat balance integral to problems of cylindrical geometry[J].Journal of Applied Mechanics，1961，28(2):310.
[17] SPARROW E M，RAMADHYANI S，PATANKAR S V.Effect of subcooling on cylindrical melting[J].Journal of Heat Transfer，1978，100(3):395-402.
[18] 帕坦卡.传热和流体流动的数值方法[M].合肥:安徽科学技术出版社，1984:83-95.
[19] 杨世铭，陶文铨.传热学(第四版)[M].北京:高等教育出版社，2006:229-280.
移动阅读