岩石节理面的存在对岩石整体强度有较大削弱作用,节理剪切力学行为一直是国内外研究热点[1-4]。节理面三维粗糙度直接影响岩体强度、变形、渗流等特征[5]。BELEM等[6]提出了5个几何参数来描述节理形貌特征,根据试验过程中参数的变化,建立起参数与节理峰值强度的关系。然而提出的剪切模型仅与节理几何特征有关,并没有从力学机理解释变化原因。TANG[7]提出了基于光照阴影的粗糙度指标,建立了基于光学试验的峰值抗剪模型。然而基于光影的BAP指标物理意义不明确,没能在力学上解释与节理剪切行为之间的关系。陈世江[8]运用多重分维普宽与广义维数阈值宽度来描述节理粗糙度,并建立起相应的节理抗剪强度模型。虽然该模型可以建立起强度与节理形貌面多重分形的关系,但该描述指标也仅是从几何角度研究形貌面。GRASSELLI等[9]提出了基于有效抵抗角的峰值抗剪模型,然而基于三角形单元划分网格具有一定的主观性,同时建立的强度模型不能反映节理形貌与膨胀角之间的关系。XIA等[10]在Grasselli 指标的基础上提出了抗剪强度模型,但存在剪胀角与基本摩擦角量纲不一致的问题。孙辅庭[11]基于等效倾角提出了新的粗糙度指标。但上述指标仅仅是对节理几何形貌特征的描述,没能将节理剪切强度与节理形貌特点从力学意义上联系起来。其他学者如唐志成[12-13]、杨洁[14]等基于Grasselli粗糙度指标提出了一系列节理峰值抗剪强度公式。但由于指标的局限,强度模型存在些许不足。
节理还分闭合、张开、充填等情形,不同接触状态的节理对其剪切强度也有不同的影响。同时节理几何尺寸的大小也会影响其剪切强度。本文主要研究目的是耦合节理的节理剪切强度,影响藕节节理剪切强度最主要的因素是节理法向应力与粗糙度。在研究节理强度前,最基础的研究是如何更为合理的描述粗糙度。笔者[15]基于长方体微凸体破坏的力学机理,提出了粗糙度指标AHD来反映节理三维粗糙度。AHD可以将节理三维粗糙度与剪切强度很好的联系起来,同时不同剪切方向的指标数值不同反映了剪切强度方向性。借助3D打印技术制备了确定节理形貌的水泥砂浆节理试样,进行了节理在不同节理粗糙度与不同法向应力情况下的剪切试验,分析了三维粗糙度与峰值抗剪强度之间的关系,建立了含有新的粗糙度指标的节理峰值抗剪强度模型。下一步在明确耦合节理的剪切强度情况下会通过提出接触状态参数来进一步考虑节理闭合、张开、充填等情形对节理剪切强度的影响,同时也会考虑几何尺寸对剪切强度的影响。
1 节理直剪试验
本节采用巴西劈裂试验获取了劈裂岩石节理表面,通过三维激光扫描技术获取了节理面形貌的高精度点云,然后通过逆向建模得到了自然岩石表面的立体模型,结合3D打印技术制作出了形貌与岩石节理表面一致的PLA模具,最后以PLA模具为底模通过水泥砂浆浇筑成型了水泥砂浆节理试样。PLA模具与水泥砂浆材料差异较大,材料在凝结过程中不易与PLA模具黏结,脱模过程中较为方便,不会破坏节理面。
所研究岩石节理形貌面是由花岗岩经巴西劈裂试验得到的。试验时,在尺寸200 mm×100 mm×100 mm岩石试块上选择200 mm×100 mm的平面,在所选表面的中心沿长轴方向画两条标记线作为劈裂试验加载中心。为防止劈裂试验完成后节理分开坠落导致节理面破坏,试验前可用保鲜膜将试块包围以免节理形成后分散。进行竖向加载时设置加载速率为0.5 mm/min,得到劈裂节理。按上述方法进行劈裂20组岩石试块,然后选取5组节理形貌特征较大的节理试样备用。
为定量表征岩石节理形貌面粗糙度,劈裂所得花岗岩节理扫描试验是在武汉大学自制的三维激光扫描仪上进行。最终获取节理形貌图如图1所示。
图1 节理形貌面
Fig.1 Morphology of rock joints
3D打印技术具有精度高、成型快等特点,基于该技术制作了复制特定节理形貌面的模具。试验时,应用计算机三维软件设计出立体的节理样式,其节理形貌基于扫描获得的5组节理面数据,设置打印精度为0.2 mm,最终基于预设模型逐层打印出了成型的5组模具。3D打印的优势在于试验的可重复性,可以精确复制模具来制作水泥砂浆节理。
节理面形貌上的几何信息复杂无序,相近的位置几何形貌也会有很大的不同。为了能够合理的复制节理面的形貌,所选用的材料应基本消除粒径对复制准确度的影响。本节制作复制结构面所选取的细骨料为标准砂,可在浇筑过程中减小对节理面形态的影响。为复制出节理微小的结构,材料选择42.5R基准水泥、标准砂和水,质量配合比为水∶水泥∶砂=1∶2.3∶4.5。试模采用铸铁试模,尺寸为200 mm×100 mm×100 mm,试模内部表面要清理干净。制作时,将PLA模具放在铸铁试模内并保持节理面向上。在PLA模具上刷少量均匀的润滑油,然后将搅拌均匀的水泥砂浆一层一层浇筑在打印模具表面并充分振捣。最后磨平铸铁模具顶面获得上盘节理。试块拆模应在砂浆达到一定强度后进行,并保证不得有边角损坏。最终获得20组耦合节理面。
在节理试块制作过程中制备了5个高度为100 mm,直径为50 mm的圆柱形砂浆试件。为保证材料性质一致,在制作过程中测试力学参数所用砂浆柱与剪切试验节理配合比相同、振捣过程一致,养护条件均一致。在岩石三轴伺服试验机上进行单轴以及三轴压缩试验,测定其平均单轴抗压强度为29 MPa、平均内摩擦角为35°。由倾斜试验获得平均基本摩擦角为32°。
将20组试样按形貌面分为5组,每组进行法向应力分别为0.5,1.0,1.5,2.0 MPa的直剪试验。首先按照速率为0.10 kN/min在试块上施加法向荷载,达到预定值稳定后通过伺服调整荷载加载方式为位移加载,速率为0.5 mm/min施加切向荷载。试验过程中记录了剪位移、剪荷载等试验数据。得到20组直剪试验峰值抗剪强度见表1。
表1 节理峰值抗剪强度试验结果
Table 1 Test results of peak shear strength of joints
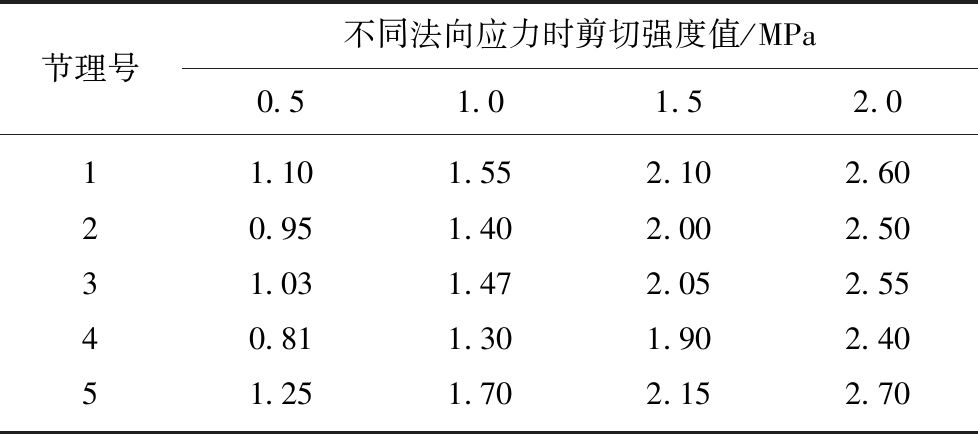
节理号不同法向应力时剪切强度值/MPa0.51.0 1.52.011.101.552.102.6020.951.402.002.5031.031.472.052.5540.811.301.902.4051.251.702.152.70
2 新的粗糙度指标简介
笔者[15]将节理面微凸体等效为长方体微凸体并研究了长方体微凸体的破坏模式。如图2所示,几何参数m=h/l决定了长方体微凸体的破坏模式,当m<mc时,破坏模式为剪胀破坏,如图2(a)所示。当m>mc时,破坏模式为剪断破坏,如图2(b)所示。图2中,N为法向荷载;T为剪切荷载;h,l,m分别为微凸体高度,宽度,高宽比;ms为临界几何参数,研究发现,长方体微凸体峰值抗剪强度随着微凸体高度增大而增大,当微凸体高度大于lmc时,其对强度有贡献的高度为lmc,微凸体高度继续增加,强度不变,其中mc与完整岩石的峰值内摩擦角有关。
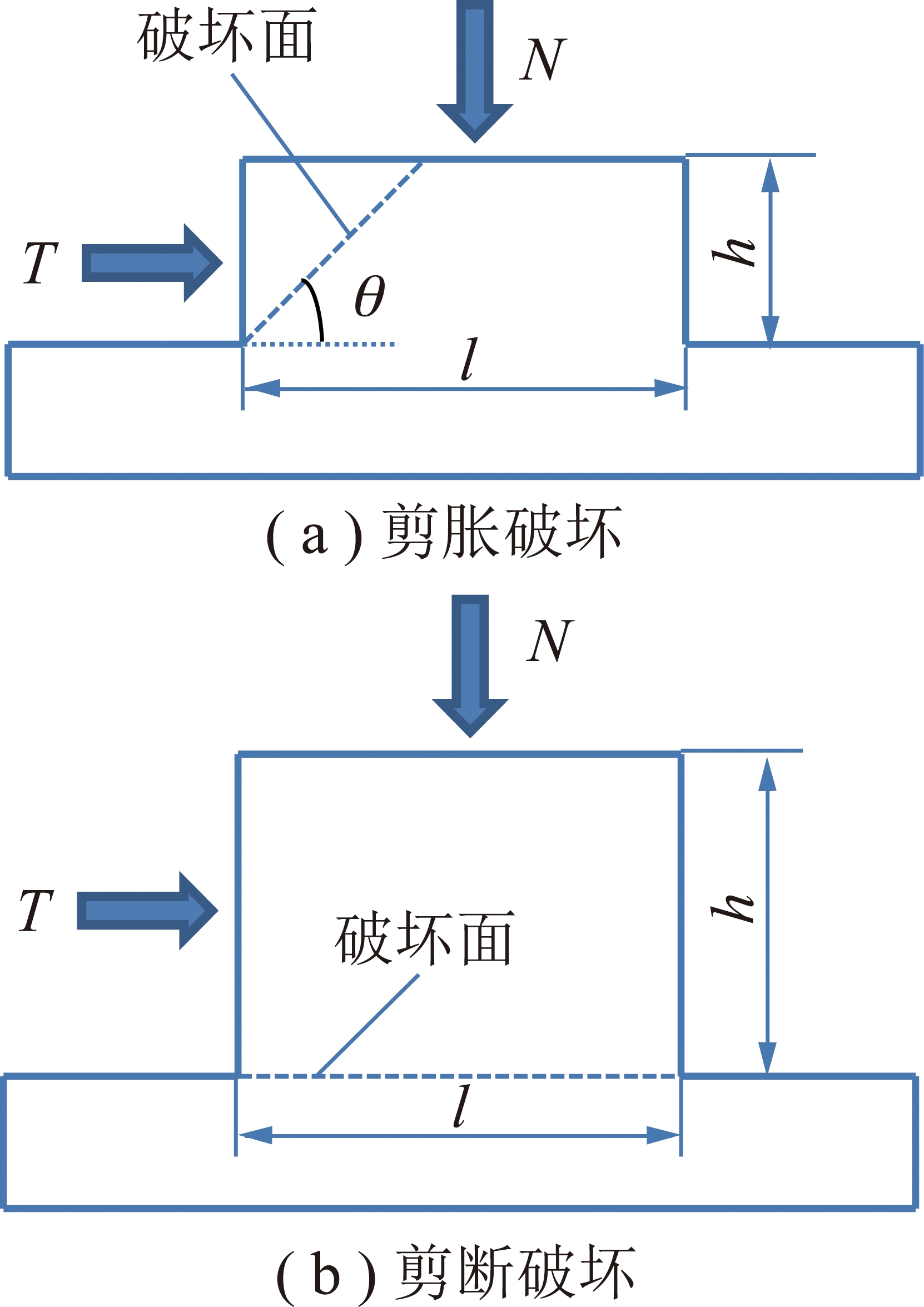
图2 长方体微凸体破坏模式
Fig.2 Failure modes of rectangular-shaped asperity
将节理面按照一定网格密度等效为一系列连续的长方体微凸体,提出了一种确定其计算高度的方法。对于长方体微凸体,其沿剪切方向相对凸出来部分为对节理剪切强度的贡献高度。因此可提出等效高差的概念,其定义为对强度有贡献的高差,当宽度一定时,同种材料的微凸体剪切强度与等效高差成正比。则等效高差![]() 为
为
![]()
(1)
式中,Hn为第n个微凸体高度。
将等效高差沿长度方向平均,得到可以反映不同破坏方式对强度贡献比例的粗糙度指标:平均等效高差AHD[15]。
天然节理具有自仿射分形特征,可根据分形理论来研究节理面的粗糙度。在不同测量尺度δ下获得节理面粗糙度指标AHD(δ),当δ=1 mm时,AHD(δ)为AHD,其数值与测量尺度δ之间存在幂定律的关系,进而提出了分形的粗糙度指标DAHD[15]。
平均等效高差AHD表征了不同破坏形式的微凸体对强度的贡献,可反映节理面的起伏方向性;分形粗糙度AHD0实质为测量尺度为1 mm的平均等效高差;DAHD反映了不同尺度AHD的关系,可全面描述节理面信息。结合两个粗糙度指标AHD0与DAHD,可提出描述形貌面剪切强度特征的粗糙度指标系统,两者指标的具体组合形式可由理论分析结合试验结果得到。
3 粗糙度新指标与剪切强度之间的关系

图3 节理等效高差与节理磨损对比
Fig.3 Equivalent height difference distribution and the wear distribution of joint surface
将节理形貌面等效为宽度为1 mm的一系列长方体微凸体,绘制节理试验所取剪切方向的等效高差分布图,如图3中左侧一列。其中白色区域代表等效高差为0,表示该区域微凸体未破坏;黑色区域为等效高差为0~mc,表示该区域微凸发生剪胀破坏;蓝色区域等效高差为mc,表示该区域微凸体发生剪断破坏。图3右侧一列为经历剪切后的节理图。对比发现节理磨损的范围与等效高差分布图中蓝色范围基本一致,并且在蓝色区域较大且成片的区域磨损较为严重。节理1蓝色区域分布较为均匀,对应磨损图中磨损的位置分布也较为均匀。节理2蓝色部分主要集中在左半部分,中部蓝色部分很少。对比磨损图可见左半部分磨损严重,中部基本没有磨损。节理3中部蓝色区域较大且成片,对比磨损图中恰好反映了蓝色区域的分布特点。而节理4蓝色区域较小且不连续,对比磨损图中可见磨损的范围较小且较为零星。节理5的磨损范围小于等效高差范围,可能是由于节理施加法向应力较小,剪切磨损不够明显,在图片上显示不出来的缘故。但节理5磨损区域也恰好对应蓝色区域密度较大部分。这些吻合说明蓝色区域对节理抗剪具有重要作用,同时表明基于等效高差分布所提的粗糙度指标具有一定的合理性。
分形粗糙度AHD0实质为测量尺度为1 mm的平均等效高差,两者物理意义一致。从长方体微凸体的破坏模式以及微凸体破坏理论上可知其大小反映了节理形貌特征对强度的贡献。根据试验结果,节理峰值抗剪强度与法向应力比值和粗糙度指标AHD0的关系如图4所示。
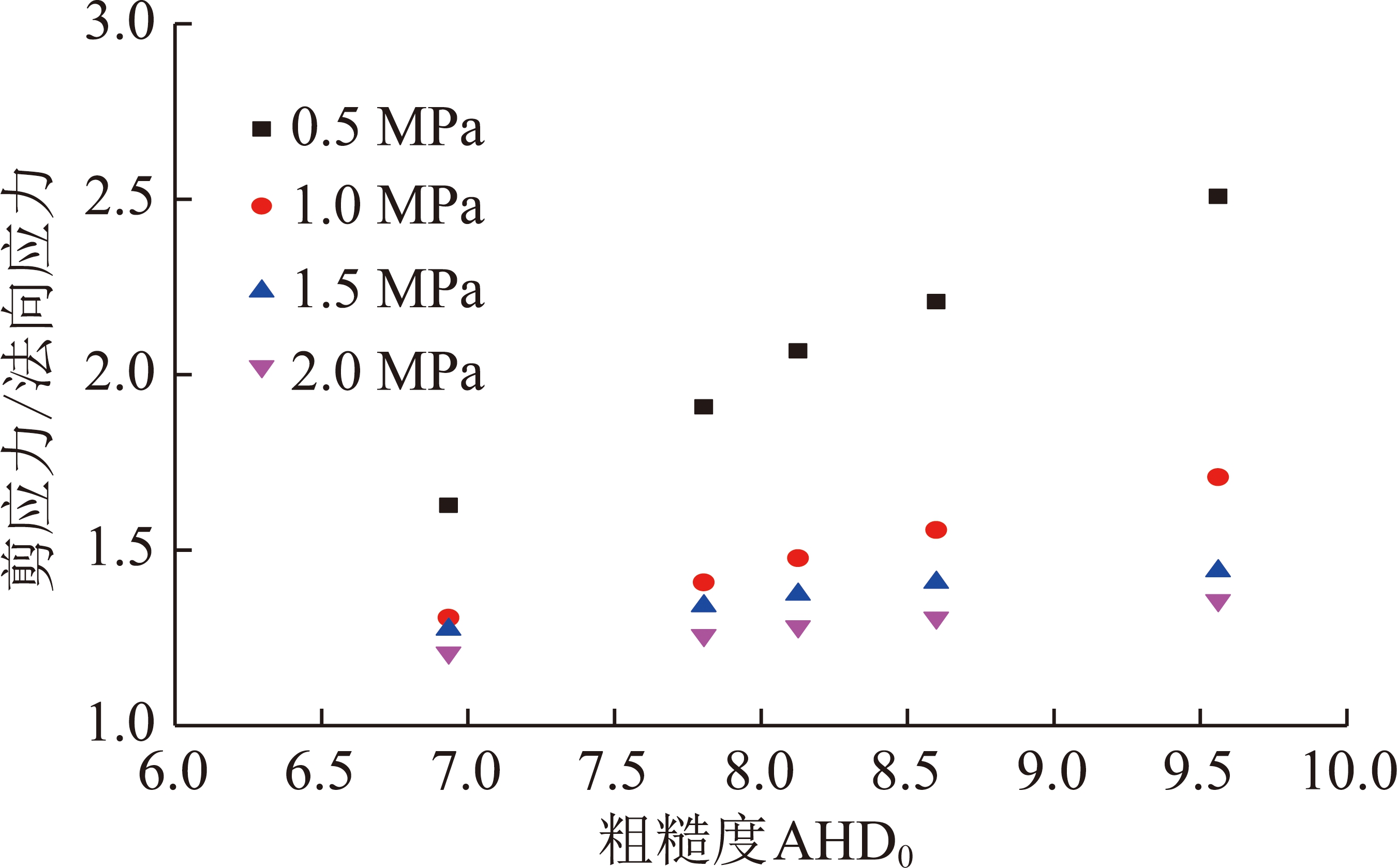
图4 节理峰值抗剪强度与法向应力比值和粗糙度 指标AHD0的关系
Fig.4 Relationship between the ratio of peak shear strength to normal stress and roughness parameter AHD0
由图4可知在相同法向应力情况下,节理峰值抗剪强度与法向应力比值和粗糙度指标AHD0成线性相关关系。不同法向应力所对应斜率不同,这是因为法向应力影响了节理的峰值膨胀角变化趋势。总体来说节理峰值抗剪强度与法向应力比值随着粗糙度指标AHD0增大而增大,同时等效高差分布情况与节理磨损情况具有良好的一致性也可反映出节理峰值抗剪强度与粗糙度指标AHD0表现出良好的相关性。
分形维数DAHD表征了不同测量尺度下粗糙度指标AHD之间的关系,可从不同尺度全面描述节理面信息。研究表明[16]分形维数越大,节理形貌含有更多的复杂精细的结构,在法向应力存在时尤其是法向应力较大时节理面越容易磨损。由此可推断,在粗糙度指标AHD0一定的情况时,节理分形维数越大其峰值抗剪强度越小。根据试验结果,节理峰值抗剪强度与法向应力比值和粗糙度指标DAHD的关系如图5所示。
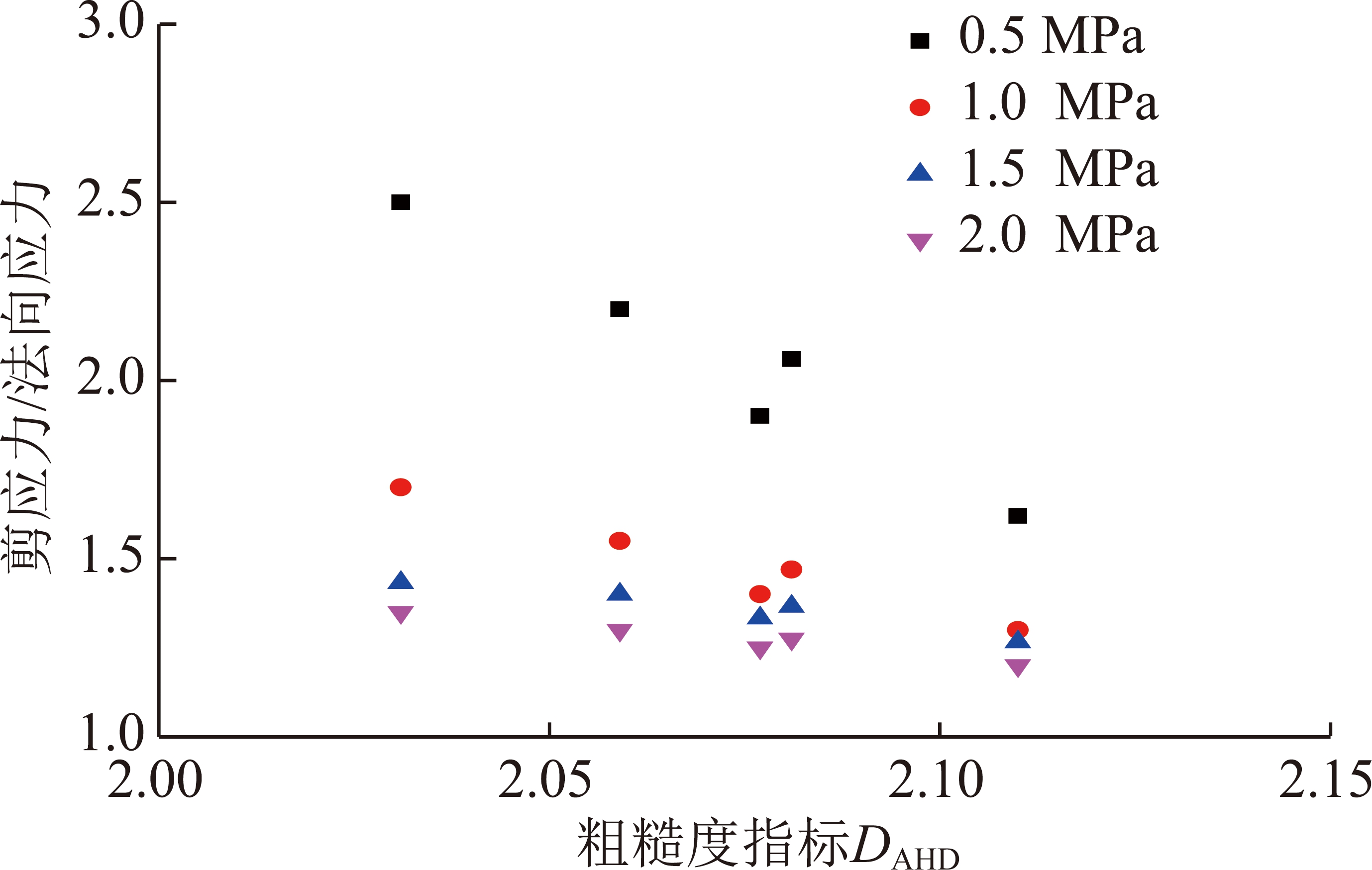
图5 节理峰值抗剪强度与法向应力比值和粗糙度 指标DAHD的关系
Fig.5 Relationship between the ratio of peak shear strength to normal stress and roughness parameter DAHD
由图5可知节理峰值抗剪强度与法向应力比值随着粗糙度指标DAHD增大而减小,表现出良好的相关性。
4 节理峰值抗剪强度模型
对于没有填充物的耦合节理,其峰值抗剪强度由两部分组成。其中一部分是由节理基本摩擦角影响;另一部分为峰值摩擦角影响,与节理类型、法向应力、节理粗糙度有关。当节理为规则齿形,此时可得到Patton模型[17]。然而Patton公式并没有考虑峰值膨胀角随着法向应力变化而变化的现象。岩石节理受剪切作用时,随着法向应力的变化节理基本摩擦角不变而峰值膨胀角会变化从而引起剪切强度的变化。因此研究节理面抗剪强度的重点是如何表征峰值膨胀角。BARTON[18]通过JRC(节理粗糙度系数)与JCS(节理面壁强度)两个参数来预测峰值膨胀角,本文也尝试用新的粗糙度指标与岩石单轴抗压强度来预测各法向应力情况下峰值膨胀角。
为此需提出一个描述峰值膨胀角随法向应力变化的函数,该函数需满足下述边界条件:当正应力趋近于0时,峰值膨胀角趋近初始膨胀角;当正应力趋近于无穷大时,峰值膨胀角趋近0。
σn→0⟹i=ip0 σn→ ⟹i=0
⟹i=0
(2)
式中,ip0为初始膨胀角;σn为法向应力。
研究表明[19-20]节理峰值膨胀角随着法向应力增大而减小,同时BARTON和CHOUBEY[21] 研究指出节理峰值抗剪强度与节理面的抗压强度和法向应力的比值有关。结合式(2)边界条件,峰值膨胀角i可由下述形式的函数预测:
![]()
(3)
其中,σc为单轴抗压强度;b为试验所待定系数。
对于确定岩石种类的节理,初始膨胀角仅与表面形貌有关。由文献[21]可知ip0仅与JRC有关,KUSUMI[22]利用一个统计公式来预测初始膨胀角。节理破坏模式可分为剪胀破坏与剪断破坏,而新提出的粗糙度指标反映了这一力学过程,因此表示初始膨胀角的模型中应存在粗糙度指标项。考虑到节理峰值抗剪强度与粗糙度指标AHD0成正相关,与粗糙度指标DAHD呈负相关,因此可构造函数
![]()
(4)
因此可得峰值抗剪强度模型为
![]()
(5)
其中,a与b为试验数据回归拟合参数;φb为基本摩擦角;τ为峰值抗剪强度。式(5)反映了影响峰值抗剪强度的主要因素,其他因素通过拟合系数来体现。
节理峰值抗剪强度公式是一个剪胀类型的强度公式。其中峰值膨胀角表达式物理意义清晰,反映了膨胀角由初始膨胀角开始随着节理法向应力的增大而减小的规律。模型的实质还为Patton剪胀型模型,较之改进的地方在于引入了可反映节理强度特征的三维粗糙度指标和反映膨胀角随法向应力变化的趋势。
通过20组节理剪切试验数据回归分析可得,a=4.9,b=16.4。因此抗剪强度模型为
![]()
(6)
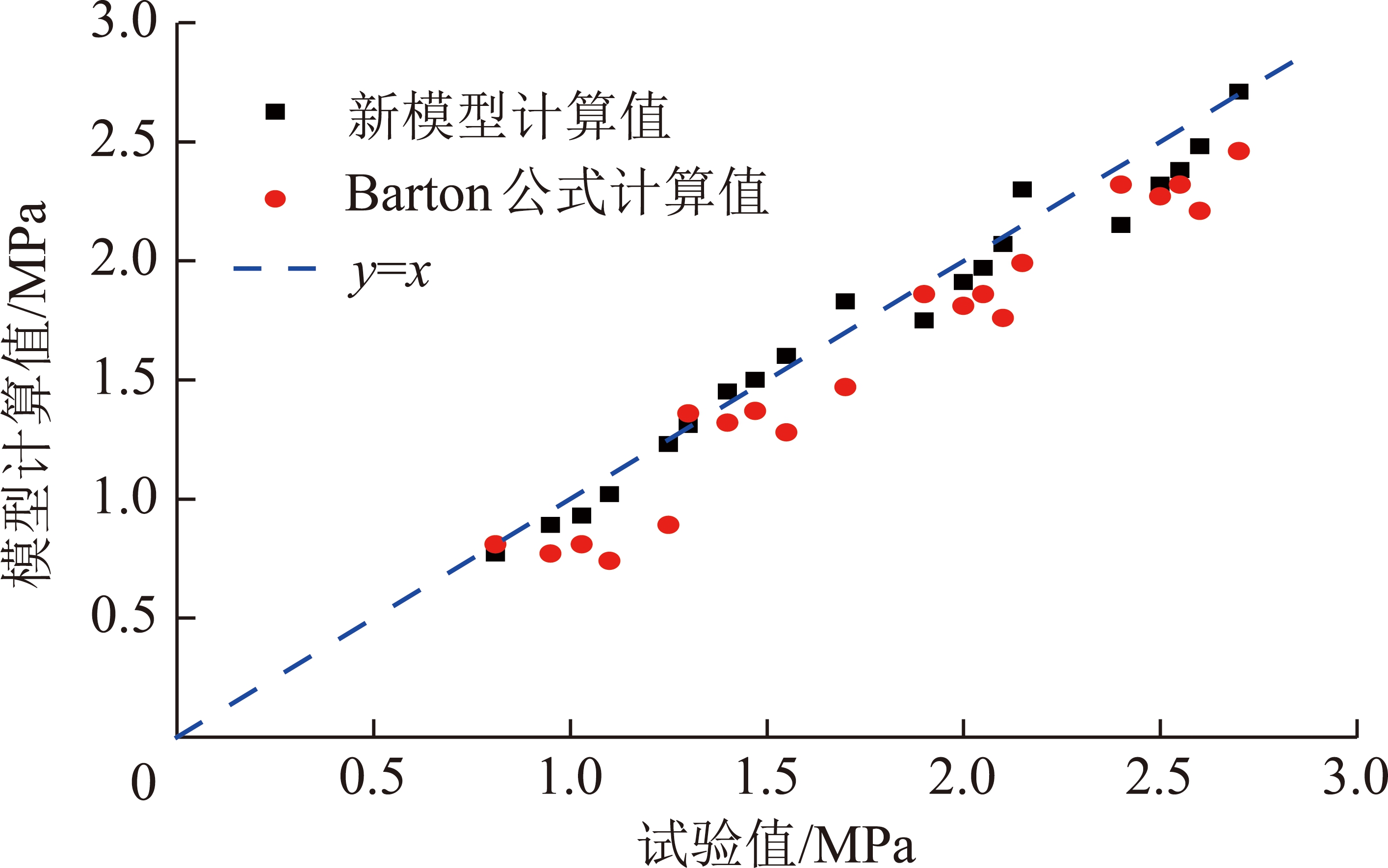
图6 试验结果、新模型以及Barton模型结果对比
Fig.6 Comparison of test results and calculation results of new model and Barton model
为验证峰值抗剪强度新模型的合理性,以及应用新模型预测节理峰值抗剪强度的有效性。图6对比了峰值抗剪强度的试验结果、新模型计算结果以及Barton公式计算结果。其中Barton公式中参数JRC是通过每个节理面沿剪切方向每隔10 mm获取一条节理剖面线,并结合TSE[23]建立的公式确定的JRC平均值。
由图6可见Barton公式与新模型计算结果均分布在蓝色直线附近,表明两种模型均能较好的计算得到节理峰值抗剪强度。然而有一半新模型计算值的离散点落在了蓝色直线上,其他离散点也落在了直线附近,表明新模型计算结果精度较高。而Barton公式计算结果的离散点大部分落在蓝色直线的下方,表明Barton公式计算结果小于试验结果。新模型与Barton公式结果对比发现新模型与试验结果误差相对较小。
5 新模型简化模型
新模型中需要获取节理面两个粗糙度指标AHD0与DAHD。计算AHD0时可在采样间距为1 mm情况下计算节理形貌面AHD指标,该过程只需要一步即可。计算DAHD时需要获取至少2个采样间距的AHD指标数值,并且还需数值拟合才能求得指标DAHD。相对于AHD0来说,指标DAHD的确定较为麻烦。朱小明等[24]研究表明高阶微凸体相对于一阶与二阶微凸体来说对强度的贡献较小。分析初始膨胀角表达式发现DAHD对峰值抗剪强度的影响较小。同时由以上节理粗糙度计算结果可知,对于一般自然节理DAHD变化范围较小。那么是否可在强度模型中去掉粗糙度指标DAHD项而将其影响通过调整a,b拟合系数来考虑。为此构造简化模型
![]()
(7)
通过20组节理剪切试验结果回归分析可得a=4.8,b=16.4。
则新模型可简化为
![]()
(8)
对比式(6)与(8)可知模型简化后仅拟合系数a由4.9变为4.8,而系数b并没有变化。这一特点可间接验证上述猜想:粗糙度指标DAHD对节理峰值抗剪强度影响较小,可调整拟合系数来考虑其影响。
将全部节理峰值抗剪强度计算值(新模型计算值、新模型简化模型计算值与Barton公式计算值)与试验值对比如图7所示,3种模型计算结果均分布在蓝色直线附近,表明3种模型均能较好的预测节理峰值抗剪强度。由图7可知,新模型计算值标准偏差0.113(对应相对偏差5%);Barton公式计算值标准偏差0.232(对应相对偏差12%);新模型简化结果标准偏差0.119(对应相对偏差5.5%)。定量分析新模型与新模型简化计算结果与试验结果的标准偏差可见新模型较新模型简化结果标准偏差小,可知新模型简化后其计算精度有所降低但由于所需参数减小计算较为方便。定量分析Barton公式与新模型简化计算结果与试验结果的标准偏差可见新模型简化结果较Barton公式标准偏差小,可知新模型简化结果精度虽然有所下降但是还是比Barton公式结果精度高。由此也可验证粗糙度指标DAHD对节理峰值抗剪强度影响较小,对其主要影响的是粗糙度指标AHD0。对于岩石工程中边坡情况,0.1~2.0 MPa的应力范围相当于10~80 m的负载深度。人们普遍认为,在大多数岩石工程(边坡)问题,作用于岩石节理的正应力在这个区域[21]。本文所提公式经过试验验证具有一定的合理性,试验法向应力范围为1~2 MPa,该应力范围可包含岩石节理剪切大部分工程情况。
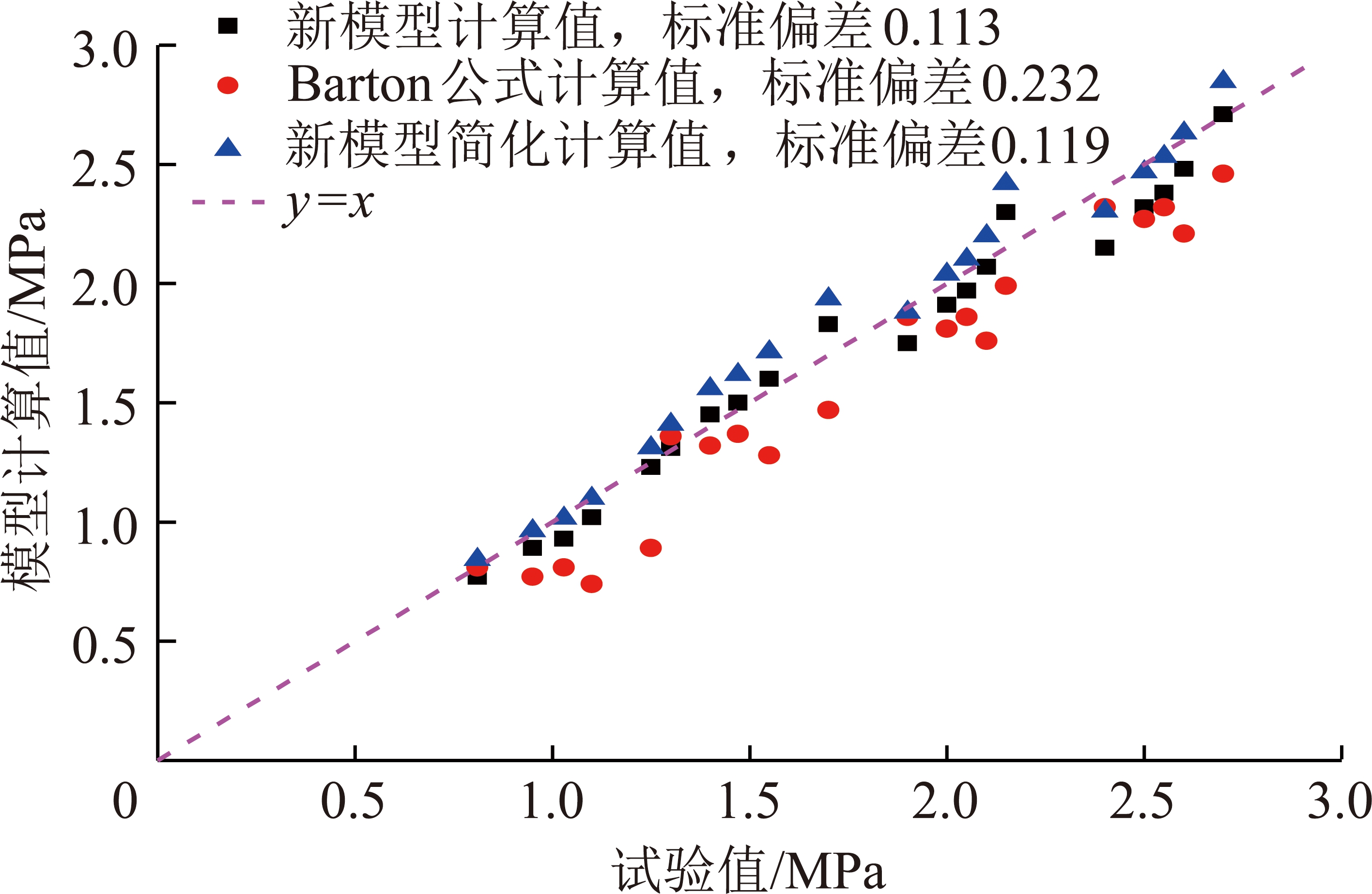
图7 峰值抗剪强度的试验结果以及计算结果对比
Fig.7 Comparison of test results and calculation results
6 结 论
(1)进行了具有5组形貌面的20个水泥砂浆节理在不同法向荷载情况下的节理剪切试验,得到了节理剪切位移-荷载曲线。分析了典型的节理剪切位移-荷载曲线特征。
(2)节理经过剪切历程后形貌面出现不同程度的磨损,其磨损范围与等效高差分布范围基本一致,并且在等效高差为蓝色区域较大且成片的区域磨损较为严重。表明等效高差图中蓝色区域对节理抵抗剪切作用较为明显,同时也反映基于等效高差分布所提的粗糙度指标具有一定的合理性。
(3)提出了具有新粗糙度指标的节理峰值抗剪强度模型,验证了新模型能够较好的计算节理峰值抗剪强度。
(4)研究发现粗糙度指标DAHD对节理峰值抗剪强度的影响较小,在新模型基础上提出了一个简化模型。将新模型计算结果、简化计算结果与试验结果和Barton公式结果对比发现新模型简化后其计算精度较新模型有所降低但由于所需参数减小计算较为方便,新模型简化结果精度虽然有所下降但是还是比Barton公式结果偏差小。
[1] WANG W L,WANG T T,SU J J,et al.Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake[J].Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research,2001,16(3):133-150.
[2] RODRIGUEZ C E,BOMMER J J,CHANDLER R J.Earthquake-induced landslides:1980-1997[J].Soil Dynamics & Earthquake Engineering,1999,18(5):325-346.
[3] 张振宇,李豪杰,贾长恒,等.带有橡胶垫层混凝土接触摩擦特性的试验研究[J].矿业科学学报,2018,3(1):20-28.
ZHANG Zhenyu,LI Haojie,JIA Changheng,et al.Characteristics of direct shear test for plain concrete joint with rubber cushion[J].Journal of Mining Science and Technology,2018,3(1):20-28.
[4] 陶志刚,庞仕辉,张博,等.大尺度边坡岩体开裂解体破坏规律试验研究[J].矿业科学学报,2016,1(3):222-227.
TAO Zhigang,PANG Shihui,ZHANG Bo,et al.Experimental study on failure law of cracking and disintegration of rock mass in large-scale slope[J].Journal of Mining Science and Technology,2016,1(3):222-227.
[5] 班力壬,戚承志,单仁亮,等.考虑微凸体曲率半径变化的GW改进模型[J].矿业科学学报,2018,3(5):442-450.
BAN Liren,QI Chengzhi,SHAN Renliang,et al.An improved GW model considering the changing curvature radius of asperities[J].Journal of Mining Science and Technology,2018,3(5):442-450.
[6] BELEM T,HOMAND-Etienne F,SOULEY M.Quantitative parameters for rock joint surface roughness[J].Rock Mechanics & Rock Engineering,2000,33(4):217-242.
[7] TANG H,GE Y,WANG L,et al.Study on estimation method of rock mass discontinuity shear strength based on three-dimensional laser scanning and image technique[J].Journal of Earth Science,2012,23(6):908-913.
[8] CHEN S J,ZHU W C,YU Q L,et al.Characterization of anisotropy of joint surface roughness and aperture by variogram approach based on digital image processing technique[J].Rock Mechanics & Rock Engineering,2016,49(3):855-876.
[9] GRASSELLI G,EGGER P.Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J].International Journal of Rock Mechanics & Mining Sciences,2003,40(1):25-40.
[10] XIA C C,TANG Z C,XIAO W M,et al.New peak shear strength criterion of rock joints based on quantified surface description[J].Rock Mechanics & Rock Engineering,2014,47(2):387-400.
[11] 孙辅庭,余成学,万利台,等.基于三维形貌特征的岩石节理峰值剪切强度准则研究[J].岩土工程学报,2014,36(3):529-536.
SUN Futing,SHE Chengxue,WAN Litai,et al.Peak shear strength criterion for rock joints based on three-dimensional morphology characteristics[J].Chinese Journal of Rock Mechanics and Engineering,2014,36(3):529-536.
[12] 唐志成,刘泉声,刘小燕.节理的剪切力学性质与含三维形貌参数的剪切强度准则比较研究[J].岩土工程学报,2014,36(5):873-879.
TANG Zhicheng,LIU Quansheng,LIU Xiaoyan.Shear behavior of rock joints and comparative study on shear strength criteria with three-dimensional morphology parameters[J].Chinese Journal of Rock Mechanics and Engineering,2014,36(5):873-879.
[13] 唐志成,夏才初,宋英龙.粗糙节理的峰值抗剪强度准则[J].岩土工程学报,2013,35(3):571-577.
TANG Zhicheng,XIA Caichu,SONG Yinglong.New peak shear strength criteria for rough joints[J].Chinese Journal of Rock Mechanics and Engineering,2013,35(3):571-577.
[14] YANG J,RONG G,HOU D,et al.Experimental study on peak shear strength criterion for rock joints[J].Rock Mechanics & Rock Engineering,2016,49(3):821-835.
[15] 班力壬,戚承志,单仁亮,等.一种新的表征岩石节理粗糙度指标系统[J].煤炭学报,2018,3(5):442-450.
BAN Liren,QI Chengzhi,SHAN Renliang,et al.A new 3D roughness parameter system for rock joint[J].Journal of China Coal Society,2018,3(5):442-450.
[16] SUN F T,JIANG Q R,SHE C X.Research on three-dimensional roughness characteristics of tensile granite joint[J].Applied Mechanics & Materials,2012,204-208:514-519.
[17] PATTON F D.Multiple modes of shear failure in rock[A].Proceeding of the Congress of International Society of Rock Mechanics[C].1966:509-513.
[18] BARTON N.Review of a new shear-strength criterion for rock joints[J].Engineering Geology,1973,7(4):287-332.
[19] SCHNEIDER H J.The friction and deformation behaviour of rock joints[J].Rock Mechanics,1976,8(3):169-184.
[20] JING L.Numerical modeling of jointed rock masses by distinct element method for two,and three dimensional problems[D].Lulea:Lulea University of Technology,1990.
[21] BARTON N,CHOUBEY V.The shear strength of rock joints in theory and practice[J].Rock Mechanics,1977,10(1-2):1-54.
[22] KUSUMI H,TERAOKA K,NISHIDA K.Study on new formulation of shear strength for irregular rock joints[J].International Journal of Rock Mechanics & Mining Sciences,1997,34(3-4):168-183.
[23] TSE R,CRUDEN D M.Estimating joint roughness coefficients[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1979,16(5):303-307.
[24] 朱小明,李海波,刘博,等.含一阶和二阶起伏体节理剪切强度的试验研究[J].岩石力学与工程学报,2011,30(9):1810-1818.
ZHU Xiaoming,LI Haibo,LIU Bo,et al.Experimental study of shear strength of joints with first-order and second-order asperities[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(9):1810-1818.
