我国煤层瓦斯抽采过程中长期存在抽采率低下等问题,平均瓦斯抽采浓度仅为30%[1-2]。因此,如何保障封孔质量、增强瓦斯抽采效果,是亟待解决的问题,也是矿井安全生产的重要保证[3]。
目前,煤岩体注浆技术是瓦斯抽采钻孔常用封孔方法。其原理是通过把某些可凝浆液注入到煤岩体的裂隙或孔隙中,使煤岩体形成强度高、抗渗性好、稳定性高的新结构体,从而改善煤岩体的物理力学性能,提高煤岩体稳定性[4-5]。因此,深入研究煤岩裂隙中浆液扩散过程及渗透率变化规律、揭示浆液封堵裂隙机理,对于指导强化抽采钻孔封孔效果、提高瓦斯抽采效率具有重要工程意义。
目前,国内外有关学者围绕煤体注浆浆液流动扩散规律和封堵裂隙机制等科学问题开展了一系列的研究工作。例如,在浆液扩散理论模型和实验研究方面,主要考虑浆液的牛顿流体和非牛顿流体特性[6-8]、浆液的时变特性[9-14]等,对浆液在单一裂隙[15-16]、裂隙网格[17-18]中的扩散渗流规律进行研究;随着岩土工程计算技术的发展,越来越多的学者通过数值模拟手段开展相关研究,其基本思路主要是利用Monte-karlo法[19-20]、概率统计法等[21]数学方法模拟生成三维随机裂隙网络,在浆液流动理论模型的基础上,对不同影响因素下的注浆扩散与岩土性质变化规律开展了数值模拟研究[22-24]。此外有的学者还从微观角度对浆液在裂隙岩体内的流动扩散以及注浆行为对煤体本身微观结构变化进行了模拟[25]。
但是,目前对于浆液扩散渗透率模型主要集中在浆液的扩散流动特性研究,较少考虑浆液颗粒沉积引起的煤岩裂隙和渗透性变化的物理本质,不能够可靠的对煤样体内部浆液扩散、封堵情况进行预测分析;此外,煤岩体内部裂隙对浆液扩散有直接影响,由于注浆属于隐蔽工程,在数值模拟过程中初始孔裂隙分布不确定性使得目前研究难以精确的描述浆液运动规律和扩散范围。因此现阶段注浆理论方面的研究相对滞后于实践,以致存在较大的盲目性。
因此,在现有研究的基础上,笔者通过对裂隙煤样内部质量变化进行分析,推导并构建了浆液对裂隙煤体的堵漏降渗的变质量渗流模型;利用工业CT对裂隙煤样扫描及像素值提取,对裂隙煤体孔裂隙微观结构分析,研究裂隙煤体初始裂隙分布;开展室内试验以及数值模拟实验,对注浆浆液扩散规律及其对裂隙煤体的堵漏降渗特性开展相关研究,从注浆浆液运移和颗粒沉积的角度揭示注浆浆液封堵煤体裂隙机制,为定量分析注浆浆液颗粒运移规律、强化抽采钻孔封孔效果提供指导。
1 浆液扩散流动变质量模型的建立
根据相关研究[4,7],注浆浆液颗粒主要在煤体裂隙中迁移,随着浆液注入裂隙煤体,注浆封孔材料颗粒在流体动力以及重力的影响下发生沉积,造成裂隙变窄直至堵塞,进而影响煤体的渗透特性。在本模型建立过程中主要作以下假设:
(1)浆液颗粒不可压缩且注入浓度保持不变。
(2)浆液扩散沉积过程中不考虑应力对煤体裂隙的影响。
(3)悬浮颗粒沉积过程不可逆,即不考虑已沉积颗粒的脱离过程。
(4)注浆浆液可近似视为牛顿流体。
1.1 质量守恒方程
本文研究对象裂隙煤体及其特征微元示意图(图1),微元体基质块长度为a,裂隙宽度为b。煤岩体裂隙中浆液固体颗粒的质量密度可以认为和煤岩体骨架相同,记为ρs;液体的质量密度记为ρf;裂隙中沉积颗粒体积分数记为S,悬浮颗粒体积分数记为C,裂隙煤岩裂隙率记为φf,体积为(a+b)3,则微元体裂隙中浆液颗粒的质量浓度可表示为
![]()
(1)
注浆浆液颗粒的迁移可以看作是对流和扩散的共同作用,忽略扩散作用,在xi(i=x,y,z)方向上,对流作用下单位时间内进入微元体的颗粒质量为
ρsg(b2+2ab)vi
(2)
式中,vi为浆液流动速度分量。
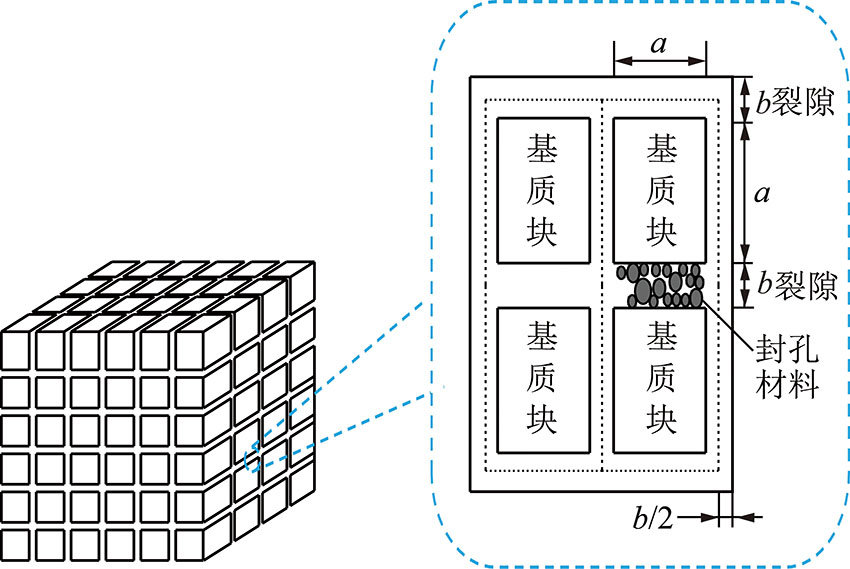
图1 裂隙煤体及特征微元示意
Fig.1 Schematic diagram of fractured coal body and characteristic micro-element
根据连续性可得,单元体上表面流出的颗粒质量为
![]()
(3)
在xi方向单位时间净流入的颗粒质量为
![]()
(4)
由于颗粒扩散作用造成的颗粒质量变化较小,此处不作考虑。同理可求得在y,z方向的颗粒质量变化。
由于颗粒沉积作用单位时间内净流入微元体质量为
CKdep(b2+2ab)(a+b)ρs
(5)
式中,Kdep为沉积系数[26]。
![]()
(6)
式中,φf0为初始裂隙率;b0为裂隙初始宽度;v为浆液流动速度;η为浆液动力黏滞系数。
根据质量守恒定律,微元体质量的增加量等于注浆封孔材料中由于沉积作用沉积的颗粒质量以及渗流作用造成的颗粒质量变化之和,整理得到
![]()
(7)
式(7)即为裂隙煤体中浆液颗粒质量守恒方程。
将式(2)代入式(6),则颗粒的质量守恒方程可改写为
![]()
 (Cφfvi)-CKdep
(Cφfvi)-CKdep
(8)
1.2 浆液流动方程
分析浆液在单裂隙内的渗流规律是研究浆液在裂隙网络内渗透扩散规律的基础。建立如图2所示浆液流动模型。
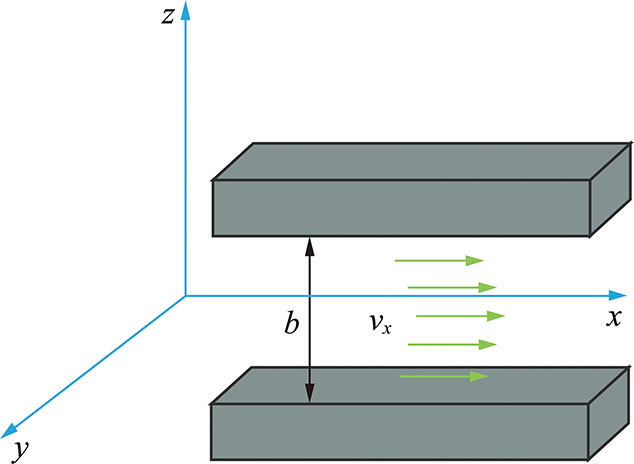
图2 单裂隙模型示意
Fig.2 Schematic diagram of single fracture model
根据相关文献[26-27],可以得到描述黏性牛顿流体的动量方程:
![]()
(9)
式中,ρ为浆液密度;p为流体压力;gi为流体质量力;σij为流体的应力分量(i,j=x,y,z)。
式(9)即为Navier-Stockes方程。
依据Navier-Stokes方程,对浆液在裂隙煤岩的单裂隙流动简化后即可获得浆液流速的表达式为
![]() (
( p+ρg
p+ρg h)
h)
(10)
由式(10)可以看出,注浆浆液的流速与裂隙的开度的平方呈正比,与压力梯度呈正比。
1.3 渗透性演化方程
对于裂隙煤体,颗粒沉积后原裂隙空间主要由沉积颗粒体积、悬浮颗粒体积(包括固体颗粒及流动液体)以及空隙体积3部分构成[28],则此时裂隙率
![]()
(11)
式中,Vd为沉积在裂隙单元体内的颗粒体积:
![]()
(12)
Vs为裂隙单元体中的悬浮颗粒体积:
![]()
(13)
将式(12),(13)代入式(11)中,得到
![]()
(14)
考虑ρs≫C得到
![]()
(15)
根据包含一阶沉积项的经典颗粒迁移-沉积模型,可以得到
![]()
(16)
![]()
(17)
ρb=(1-φf0)ρ′s+(φf0-φf)ρs
(18)
式中,ρb为煤体体积密度;ρ′s为煤骨架颗粒密度。
将式(13),(16)代入式(15)可得
![]()
(19)
煤体渗透率k与裂隙宽度之间的关系满足:
![]()
(20)
则渗透率比值:
![]()
(21)
式中,k0为煤体的初始渗透率。
综上,式(8),(10),(19),(21)共同构成了裂隙煤体浆液流动变质量渗流数学模型,利用上述模型可对注浆浆液封堵裂隙过程及煤体渗透率变化规律进行分析。
2 裂隙煤体注浆数值模型建立
2.1 注浆裂隙煤样CT扫描及渗透率测定
图3为CT扫描系统,其中,图3(a)为CT设备机械转台,机械转台上部为固定器,固定器由三爪构成,图3(b)为裂隙煤样在固定后照片,在固定前通过热熔胶条将煤样下部与橡胶棒固定,将橡胶棒另一端固定在固定器上。在煤样热缩管外部标记一纵向直线,在固定煤样时将标记线与其中一固定支脚对齐。图3(c)为注浆后煤样固定图像。图3(d)为裂隙煤样在扫描显示屏中图像,图3(e)为注浆后煤样在扫描显示屏中图像。CT实验参数设置扫描时间为50 min,生成扫描图像1 000张。

图3 CT扫描实验系统
Fig.3 CT scanning experimental system
图4为利用数值方法得到的裂隙煤样注浆前的CT重构图,可以看到煤样上端中部有一较宽裂隙近垂直向下部延伸,延伸至煤样上部1/3处向左下部延伸,延伸过程中裂隙宽度逐渐减小;在下部1/3处裂隙出现分叉,同时裂隙宽度逐渐减小,1条裂隙分支近似垂直向下部延伸,另1条裂隙向右侧延伸并发生曲折后向下部延伸至煤样底部。
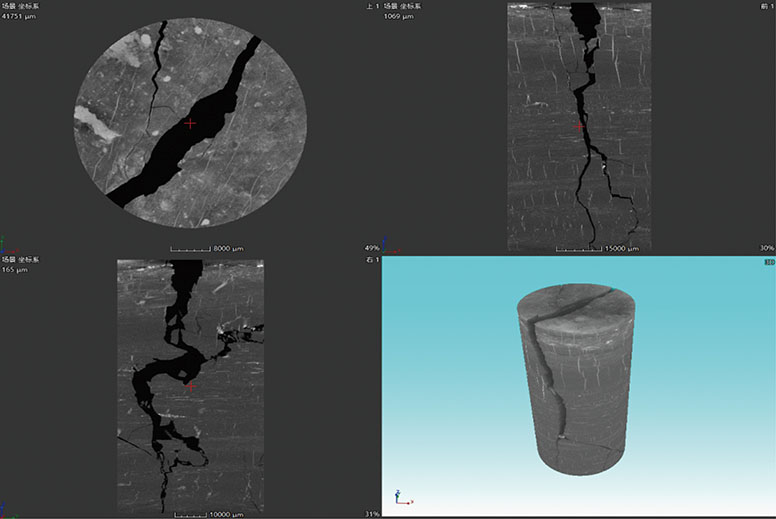
图4 裂隙煤样CT重构
Fig.4 Cracked coal sample CT reconstruction diagram

图5 注浆浆液原材料
Fig.5 Grouting slurry raw material
注浆浆液为水、固化剂、膨胀剂以及粒径小于100目的煤粉等原材料构成,如图5所示。利用自行设计的煤样注浆实验系统(图6),按表1所示注浆实验参数对裂隙煤样进行注浆。步骤如下:① 将待注浆煤样外包裹密封胶圈,将煤样从密闭腔下端塞入,将下端盖与密闭腔拧紧,下阀门处于打开状态;② 将上阀门一端与注浆管路连接,另一端与上端盖连接,上端盖下侧与密闭腔上侧连接拧紧,上阀门处于打开状态(将上端盖连接后,确保装置气密性);③ 配置注浆封孔材料,将配置好的注浆封孔材料加入手动加压泵后开始注浆试验;④ 实验过程中保持注浆压力为0.2 MPa,实验持续时间30 min后将上阀门关闭,清洗注浆管路及手动加压泵;⑤ 分别打开上下端盖,通过上部挤压将煤样推出密闭腔后干燥,将注浆气室清洗待用;⑥ 待注浆结束后,将煤样外部清洗干燥后开展CT扫描实验。
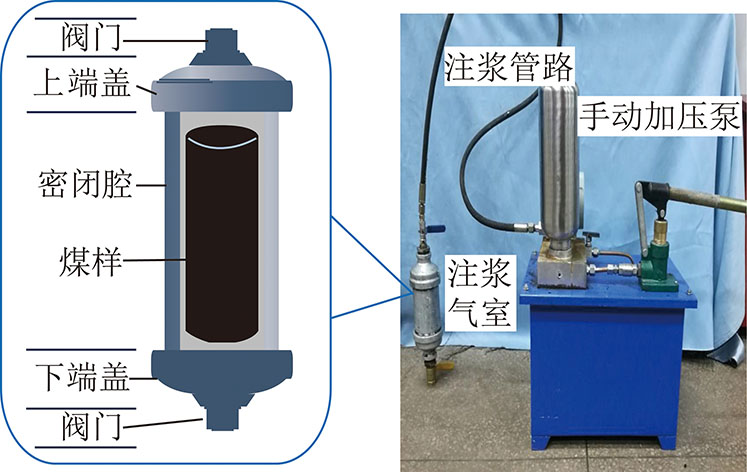
图6 煤样注浆实验系统
Fig.6 Grouting experimental system for coal sample
表1 注浆实验参数
Table 1 Grouting experimental parameters

编号注浆压力/MPa水固比黏时变性η10.21.5154.55e0.025 4t
从图7可以看出,煤样裂隙分布较为贯通,封孔材料将裂隙密实充填,且封孔材料与裂隙交界处贴合密实。在煤样下部1/3处出现分支裂隙,向右侧分支后又闭合,但右侧裂隙未被封孔材料充填。
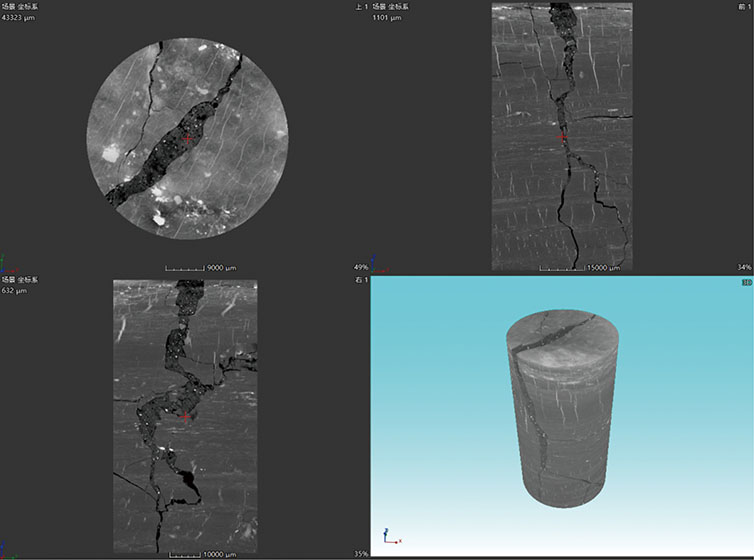
图7 煤样注浆后CT重构
Fig.7 CT reconstruction after coal sample grouting
为定量表征注浆对煤样渗透性的影响效果,文献[29-30]中的煤样渗透率测试方法,利用三轴煤岩瓦斯渗流试验系统对煤样注浆前后的渗透率进行了测试,测试条件和结果见表2。可以看到,注浆后煤样渗透率较原始大幅下降,下降幅度达95.7%。
表2 煤样渗透率测试结果
Table 2 Coal sample permeability test

编号瓦斯压力/MPa围压和轴压/MPa初始渗透率/10-15 m2注浆后渗透率/10-15 m210.21185.47.9
2.2 数值模型及边界条件
将CT重构后的裂隙煤样模型导入数值模拟软件COMSOL,得到与实验煤样尺寸一致的数值计算模型,即50 mm×100 mm的圆柱体模型,数值几何模型及网格划分如图8所示。
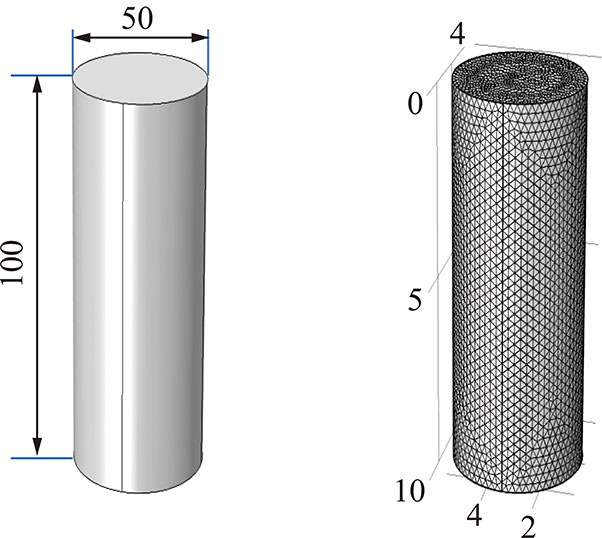
图8 模型几何及网格划分
Fig.8 Model schematic diagram
根据实验条件设置对应的数值模拟边界条件:煤样上表面设置注浆压力0.2 MPa,煤样下表面压力为0,煤样四周为无渗透边界;对于模型初始条件:模型初始浆液浓度为0,煤样初始渗透率分布可以根据初始裂隙与渗透性关系获取,图9给出了模型初始渗透率分布,可以看到,渗透率上部较大,下部较小,这是由于煤样上部裂隙开度较大,而下部裂隙开度较小。
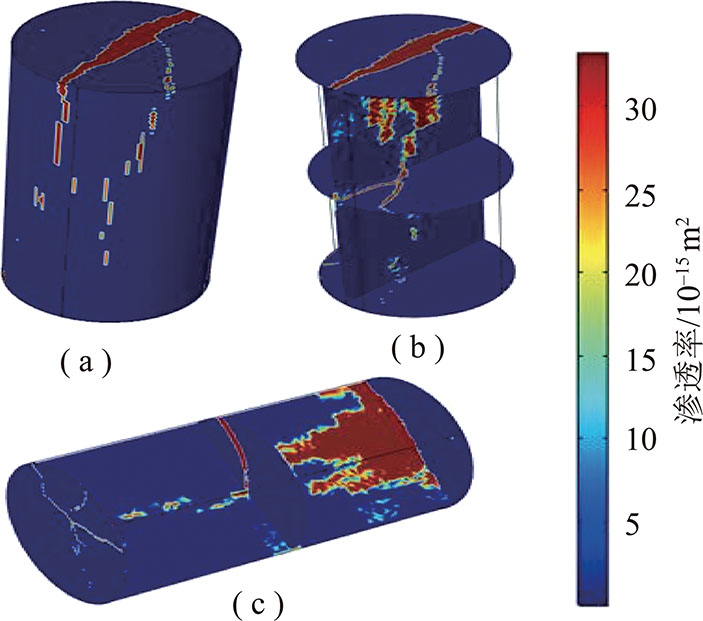
图9 模型初始渗透率分布
Fig.9 Model initial permeability coefficient distribution
3 裂隙煤体注浆数值模拟及分析
图10为注浆压力随时间变化云图。由图10可知,随着注浆时间增加,煤样注浆压力从上部逐步向下部扩散,当注浆时间为100 s时,压力分布基本贯穿煤样,表明此时注浆浆液从煤样上端流动到了下端。随着注浆时间继续增加,煤样下部注浆压力有所增大,当注浆时间为1 000 s以后,煤样注浆压力趋于稳定。还可以看到,煤样注浆压力上端较大、下部较小,特别是煤样上半部分注浆压力衰减很小,在中部附近注浆压力有明显的下降,结合CT扫描图可知,这是由于煤样上部裂隙发育,裂隙开度大,渗透性好,而煤样下部裂隙开度较小,渗透性较差。
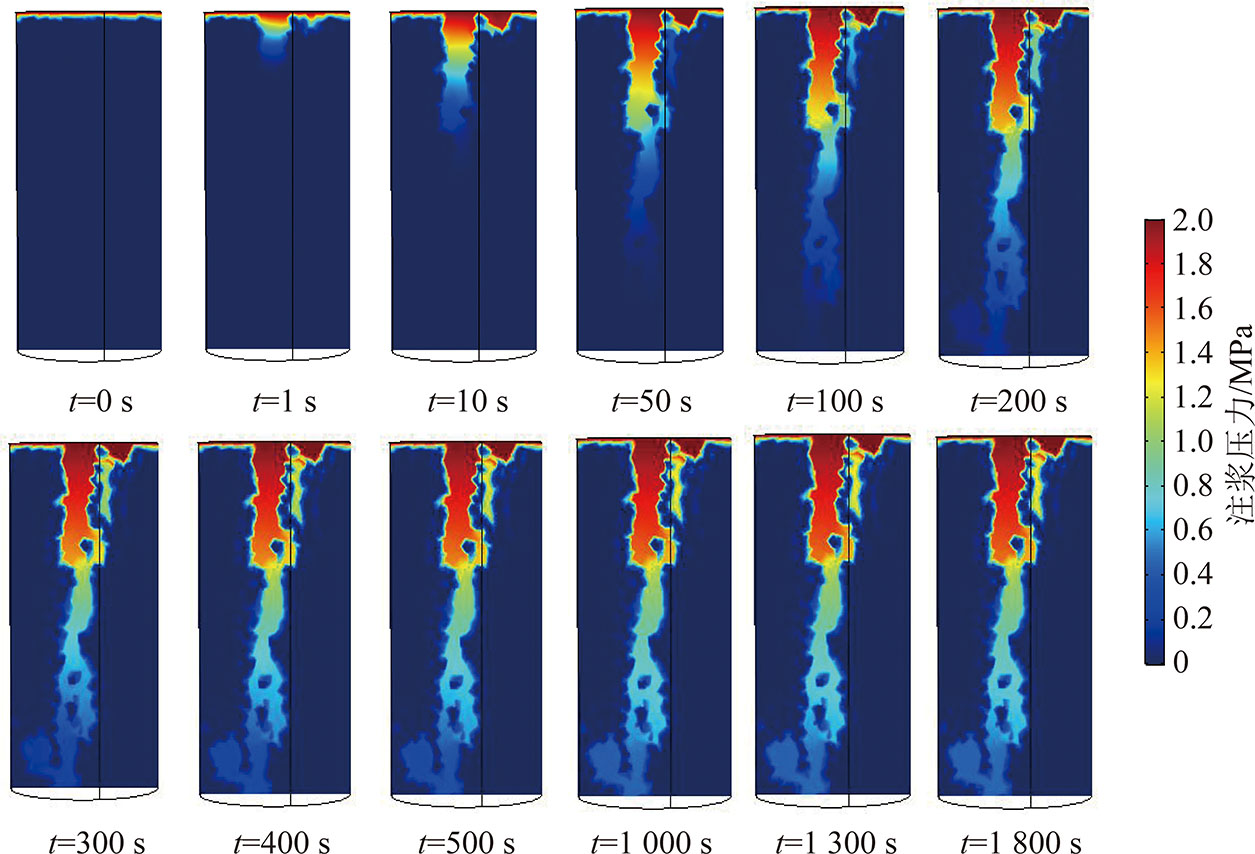
图10 注浆压力随时间变化云图
Fig.10 Grouting pressure changes with time
图11为不同时刻的煤样渗透率变化云图。从图11可以看到,随着注浆时间增加,煤样裂隙被浆液封堵,渗透率不断降低。当注浆时间为100 s时,煤样裂隙渗透率整体开始下降,表明此时注浆浆液贯穿了煤样裂隙;之后,随着注浆时间继续增加,煤样渗透率开始快速下降,当注浆时间为1 000 s以后,煤样的渗透率逐渐趋于稳定。还可以看到,在注浆作用下,煤样上端裂隙首先被封堵,渗透率快速下降,之后随着浆液扩散,煤样下部渗透率也逐渐变小,最终煤样贯通裂隙被注浆浆液封堵。
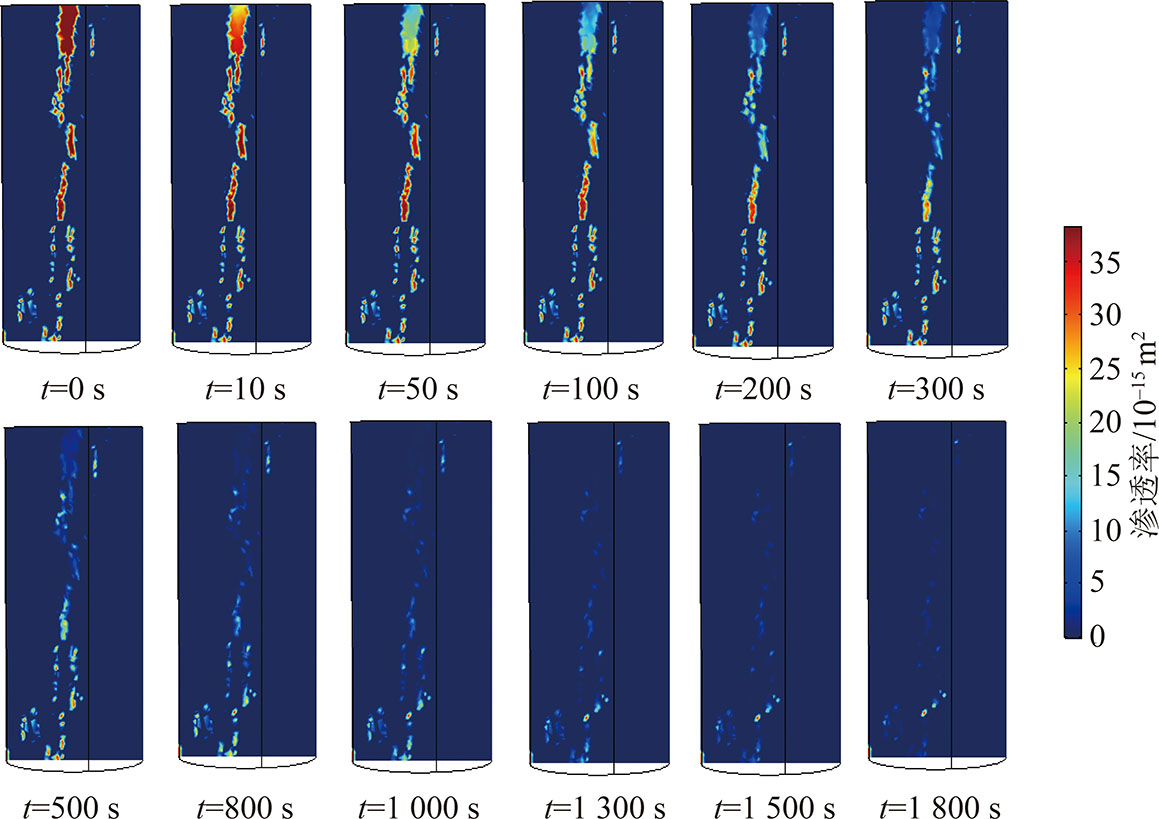
图11 渗透率随时间变化云图
Fig.11 Permeability change over time
图12为数值模拟得到的注浆过程中煤样渗透率随时间变化曲线,从图12可以看出,煤样内部裂隙分布较贯通,初始渗透率为182.0×10-15 m2,随着注浆时间的增加,煤样渗透率逐渐降低。当注浆时间为100 s时,煤样渗透率较初始下降幅度约45.1%;当注浆时间为300 s时,煤样上端部渗透率显著下降,整体渗透率下降幅度约为65.3%;当注浆时间为1 800 s后,煤样裂隙基本被注浆颗粒充填,整体渗透率下降到5.6×10-15 m2,下降幅度为96.9%。对比煤样注浆前后的渗透率实验测试结果,其值从注浆前的185.4×10-15 m2下降到最终的7.9×10-15 m2左右,下降幅度为95.7%。数值模拟结果与实验结果具有较好的一致性,验证了本文模型的正确性。
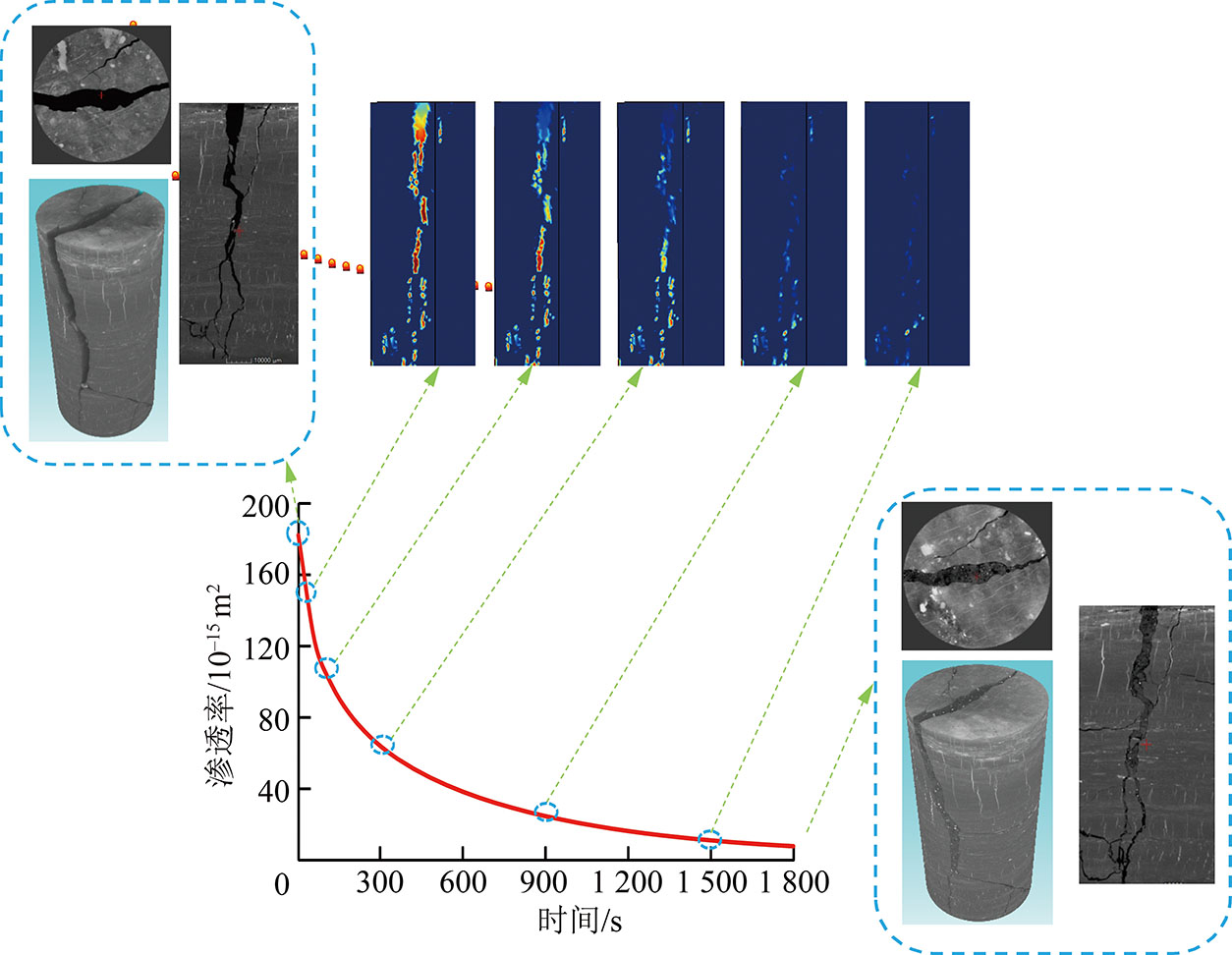
图12 煤样模型渗透率变化曲线
Fig.12 Permeability curve of coal sample model
4 讨 论
为探究注浆材料对裂隙煤岩的降渗机制,为提高瓦斯抽采钻孔封孔质量提供理论依据,针对目前理论研究中较少考虑浆液颗粒沉积引起的煤岩裂隙和渗透性变化以及数值模拟研究中初始孔裂隙分布不确定性导致难以精确的描述浆液运动规律和扩散范围的研究现状,笔者通过对裂隙煤样内部质量变化进行分析,推导并构建了考虑浆液颗粒沉积作用的裂隙煤体注浆堵漏降渗变质量渗流模型;同时,利用工业CT扫描的可以对煤岩体内部孔裂隙结构进行观测,可以解决煤岩体注浆的“黑箱”问题,实现了对煤体微观结构的“可视化”分析;在此基础上对注浆浆液扩散规律及其对裂隙煤体的堵漏降渗特性开展研究,从注浆浆液运移和颗粒沉积的角度揭示注浆浆液封堵煤体裂隙机制,为定量分析注浆浆液颗粒运移规律、强化抽采钻孔封孔效果提供指导。
本文模型模拟结果与CT扫描、煤样渗透率测定结果具有较好的一致性,证明本文模型的正确性,然而浆液沉积和封堵裂隙涉及较为复杂的物理化学过程,模型本身和研究手段等方面尚存在需进一步完善的部分。例如,注浆材料化学性质可能随时间发生变化、沉积颗粒可能重新变成悬浮颗粒等,本文对沉积过程进行了简化处理,重点考虑了浆液颗粒沉积封堵的物理结果;其次,由于实验条件等因素限制,不能够对浆液注入全过程进行CT扫描和观测分析,仅对煤样初始状态和注浆后进行了CT扫描和渗透性测试,对于浆液注浆全过程的“可视化”实现尚需实验手段的改进和升级;此外,该研究尚处于实验室条件和尺度,对于工程尺度和复杂条件下浆液的扩散规律和封堵机理尚需进一步研究。
5 结 论
(1)建立了基于沉积作用的浆液对裂隙煤体的堵漏降渗的变质量渗流模型,将渗透率变化与注浆浆液颗粒沉积过程相关联,得到连续注浆条件下裂隙率及渗透率等的变化规律。
(2)对煤样注浆前后进行渗透率进行了实验测定,煤样初始渗透率为185.4×10-15 m2,注浆之后煤样整体渗透率下降到7.9×10-15 m2,下降幅度为95.7%,注浆后渗透率值有明显减小,表明该注浆封孔材料对裂隙煤体具有明显封堵效果。
(3)本文模型数值求解得出的压力分布云图以及渗透率变化等结果与CT扫描实验中煤样内部注浆封孔材料分布有较好的一致性,验证了本模型的正确性。
[1] WANG L,CHENG Y P.Drainage and utilization of Chinese coal mine methane with a coal-methane co-exploitation model:Analysis and projections[J].Resources Policy,2012,37(3):315-321.
[2] YUAN R,CHEN C,WEI X,et al.Heat-fluid-solid coupling model for gas-bearing coal seam and numerical modeling on gas drainage promotion by heat injection[J].International Journal of Coal Science & Technology,2019 6(4):564-576.
[3] 周福宝,孙玉宁,李海鉴,等.煤层瓦斯抽采钻孔密封理论模型与工程技术研究[J].中国矿业大学学报,2016,45(3):433-439.
ZHOU Fubao,SUN Yuning,LI Haijian,et al.Research on the theoretical model and engineering technology of the coal seam gas drainage hole sealing[J].Journal of China University of Mining & Technology,2016,45(3):433-439.
[4] 张超,李树刚,曾强,等.浆液在煤岩体裂隙中渗透规律的数值模拟[J].煤矿安全,2015,46(12):19-22,26.
ZHANG Chao,LI Shugang,ZENG Qiang,et al.Numerical simulation on permeation laws of grouting in coal and rock fracture[J].Safety in Coal Mines,2015,46(12):19-22,26.
[5] 王振锋,周英,孙玉宁,等.新型瓦斯抽采钻孔注浆封孔方法及封堵机理[J].煤炭学报,2015,40(3):588-595.
WANG Zhenfeng,ZHOU Ying,SUN Yuning,et al.Novel gas extraction borehole grouting sealing method and sealing mechanism[J].Journal of China Coal Society,2015,40(3):588-595.
[6] BAKER W H.Planning and performing structural chemical grouting[A].Grouting in Geotechnical Engineering[C].ASCE,2010.
[7] 王晓晨,刘人太,张春雨,等.裂隙注浆浆液浓度分布试验研究与机制探讨[J].煤炭学报,2019,44(7):1-9.
WANG Xiaochen,LIU Rentai,ZHANG Chunyu,et al.Experimental study on concentration distribution of fracture grouting and discussion on its mechanism[J].Journal of China Coal Society,2019,44(7):1-9.
[8] 郝哲,王介强,刘斌.岩体渗透注浆的理论研究[J].岩石力学与工程学报,2001,20(4):492-496.
HAO Zhe,WANG Jieqiang,LIU Bin.Theoretical study of osmotic grouting in rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(4):492-496.
[9] 阮文军.注浆扩散与浆液若干基本性能研究[J].岩土工程学报,2005,27(1):69-73.
RUAN Wenjun.Research on diffusion of grouting and basic properties of grouts[J].Chinese Journal of Geotechnical Engineering,2005,27(1):69-73.
[10] 李术才,刘人太,张庆松,等.基于黏度时变性的水泥-玻璃浆液扩散机制研究[J].岩石力学与工程学报,2013,32(12):2415-2421.
LI Shucai,LIU Rentai,ZHANG Qingsong,et al.Research on C-S slurry diffusion mechanism with time-dependent behavior of viscosity[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(12):2415-2421.
[11] 杨志全,侯克鹏,郭婷婷,等.黏度时变性宾汉体浆液的柱-半球形渗透注浆机制研究[J].岩土力学,2011,32(9):2697-2703.
YANG Zhiquan,HOU Kepeng,GUO Tingting,et al.Study of column-hemispherical penetration grouting mechanism based on Bingham fluid of time-dependent behavior of viscosity[J].Rock and Soil Mechanics,2011,32(9):2697-2703.
[12] FREITAS T M B,POTTS D M,ZDRAVKOVIC L.A time dependent constitutive model for soils with isotach viscosity[J].Computers & Geotechnics,2011,38(6):809-820.
[13] 刘健,张载松,韩烨,等.考虑黏度时变性的水泥浆液盾构壁后注浆扩散规律及管片压力模型的试验研究[J].岩土力学,2015,36(2):361-368.
LIU Jian,ZHANG Zaisong,HAN Ye,et al.Backfilled grouting diffusion law and model of pressure on segments of shield tunnel considering viscosity variation of cement grout[J].Rock and Soil Mechanics,2015,36(2):361-368.
[14] ZHANG D M,HUANG Z K,YIN Z Y,et al.Predicting the grouting effect on leakage-induced tunnels and ground response in saturated soils[J].Tunneling & Underground Space Technology,2017,65:76-90.
[15] DUAN Y J.Study of permeation-grouting diffusion mechanism of bingham fluid based on percolation effect[J].Building Technology Development,2016,43(10):103-106.
[16] WANG L,LI T.The calculation of grouting diffusion radius on based bingham fluid for chunnel that passes through fractured rock mass[J].Applied Mechanics & Materials,2013,256-259:1280-1286.
[17] YUN S K,WHITTLE A J.Particle network model for simulating the filtration of a microfine cement grout in sand[J].Journal of Geotechnical & Geoenvironmental Engineering,2009,135(2):224-236.
[18] 罗平平,李志平,范波,等.倾斜单裂隙宾汉浆液流动模型理论研究[J].山东科技大学学报(自然科学版),2010,29(1):49-53.
LUO Pingping,LI Zhiping,FAN Bo,et al.Theoretical study on flow model for tilted single fracture binghamian grouts[J].Journal of Shandong University of Science and Technology (Natural Science),2010,29(1):49-53.
[19] 郝哲,王介强.岩体裂隙注浆的计算机模拟研究[J].岩土工程学报,1999,21(6):727-730.
HAO Zhe,WANG Jieqiang.Computerized simulation of crack grouting in rock mass[J].Chinese Journal of Geotechnical Engineering,1999,21(6):727-730.
[20] 杨米加,贺永年,陈明雄.裂隙岩体网络注浆渗流规律[J].水利学报,2001,32(7):41-46.
YANG Mijia,HE Yongnian,CHEN Mingxiong.Law of grouting penetrating through fracture network of rock mass[J].Journal of Hydraulic Engineering,2001,32(7):41-46.
[21] 陈剑平.岩体随机不连续面三维网络数值模拟技术[J].岩土工程学报,2001,23(4):397-402.
CHEN Jianping.3-D net work numerical modeling technique for random discontinuities of rock mass[J].Chinese Journal of Geotechnical Engineering,2001,23(4):397-402.
[22] 罗平平,陈蕾,邹正盛,等.空间岩体裂隙网络灌浆数值模拟研究[J].岩土工程学报,2007,29(12):1844-1848.
LUO Pingping,CHEN Lei,ZOU Zhengsheng,et al.Numerical simulation of grouting in space fracture network of rock mass[J].Chinese Journal of Geotechnical Engineering,2007,29(12):1844-1848.
[23] 李宁,张平,闫建文.灌浆的数值仿真分析模型探讨[J].岩石力学与工程学报,2002,21(3):326-330.
LI Ning,ZHANG Ping,YAN Jianwen.Numerical modeling of grouting in geoengineering[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(3):326-330.
[24] 刘健,刘人太,张霄,等.水泥浆液裂隙注浆扩散规律模型试验与数值模拟[J].岩石力学与工程学报,2012,31(12):2445-2452.
LIU Jian,LIU Rentai,ZHANG Xiao,et al.Diffusion law model test and numerical simulation of cement fracture grouting[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(12):2445-2452.
[25] 王强,冯志强,王理想,等.裂隙岩体注浆扩散范围及注浆量数值模拟[J].煤炭学报,2016,41(10):2588-2595.
WANG Qiang,FENG Zhiqiang,WANG Lixiang,et al.Numerical analysis of grouting radius and grout quantity in fractured rock mass[J].Journal of China Coal Society,2016,41(10):2588-2595.
[26] 李华伟.赤泥滤液的渗流穿透特性及污染物迁移过程研究[D].北京:北京交通大学,2015.
LI Huawei.The study on the penetration property of red mud filtrate and transport process of contaminant[D].Beijing:Beijing Jiaotong University,2015.
[27] 阮文军.基于浆液粘度时变性的岩体裂隙注浆扩散模型[J].岩石力学与工程学报,2005,24(15):2709-2714.
RUAN Wenjun.Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(15):2709-2714.
[28] 刘泉声,崔先泽,张程远.基于变孔隙率的多孔介质中悬浮颗粒沉积渗透率衰减模型研究[J].岩石力学与工程学报,2016,41(S1):3308-3314.
LIU Quansheng,CUI Xianze,ZHANG Chengyuan.Permeability reduction model of particles deposit in porous medium considering changeable porosity[J].Chinese Journal of Rock Mechanics and Engineering,2016,41(S1):3308-3314.
[29] 魏建平,位乐,王登科.含水率对含瓦斯煤的渗流特性影响试验研究[J].煤炭学报,2014,39(1):97-103.
WEI Jianping,WEI Le,WANG Dengke.Experimental study of moisture content influences on permeability of coal containing gas[J].Journal of China Coal Society,2014,39(1):97-103.
[30] 魏建平,王登科,位乐.两种典型受载含瓦斯煤样渗透特性的对比[J].煤炭学报,2013,38(S1):93-99.
WEI Jianping,WANG Dengke,WEI Le.Comparison of permeability between two kinds of loaded coal containing gas samples[J].Journal of China Coal Society,2013,38(S1):93-99.
