我国埋深在1 000 m以下煤炭资源储量为2.95万亿t，约占煤炭资源总量的53%[1]。《国家中长期科学和技术发展规划纲要》(2006—2020)明确提出:重点研究开发煤炭高效开采技术及配套装备，建设千米深井以开发深部矿物资源已成为应对能源紧缺问题的必然选择[2]。在千米煤矿深井中，提升容器以速度高达16 m/s、载重量达45 t的高速重载工况下装卸载物料，系统运行过程中，每根钢丝绳的弹性伸长变化及对应绳槽的磨损量不一致，钢丝绳会出现提升不同步现象，进而造成多钢丝绳间张力差异，当钢丝绳张力差过大时，会造成卡罐现象，甚至导致断绳、坠罐等严重安全事故，造成重大财产损失和人员伤亡。因此，有必要在提升系统运行过程中及时降低钢丝绳张力差，实现安全高效生产[3]。
当前，针对提升系统钢丝绳张力差异较大问题，应用最广泛的为液压悬挂装置[4-5]。然而，该装置安装于钢丝绳与提升容器之间，随着提升速度和提升载荷的增加，该装置的质量也必然急剧增大，造成提升容器的有效提升载荷降低。此外，由于该装置借助连通器原理完成张力调节，属于被动调节方式，钢丝绳张力调节响应速度较慢。因此，亟需研究一种钢丝绳张力主动调节方法，提高钢丝绳张力控制效果。
双绳缠绕式深井提升系统可以看作一种并联柔索系统，邵杏国等[6]设计了煤矿建井吊盘钢丝绳张力均衡控制器，提出了模糊PID控制方法调节吊盘的钢丝绳张力差。HASSAN与KHAJEPOUR[7]提出了投影法计算柔索驱动机器人执行器张力，实现绳索张力优化。然而，上述关于柔索机器人的相关控制策略并没有考虑非线性系统存在的不确定性和外部干扰，自适应反步控制[8-10]能够动态跟随系统特性的变化调节控制器的参数，在非线性系统中广泛应用。闫茂德等[11]针对一类三角结构形式的非不确定性系统，利用反步和滑模控制设计了一种状态参考自适应反步滑模控制器。在自适应反步控制理论基础上，引入自适应模糊控制设计方法，可以进一步提高控制精度[12]。文献[13-14]将模糊状态观测器和模糊滤波器结合，有效解决了一类严格反馈的状态不可测非线性不确定系统的控制问题。ZHU等[15]结合非线性干扰观测器和自适应反步控制器，提出了一种鲁棒自适应控制算法，实现了双绳缠绕式提升系统运行过程中钢丝绳张力平衡控制。然而，双绳缠绕式提升系统的钢丝绳张力控制存在输出约束问题[16]，针对该问题，文献[17-18]利用可观的度量函数——障碍李雅普诺夫函数来处理非线性系统的对称/不对称以及输出约束问题。严格反馈非线性系统在设计控制器时，通常和反步控制相结合。
针对双绳缠绕式深井提升系统，首先建立提升系统钢丝绳张力主动控制模型，进而考虑钢丝绳张力反馈信号存在的无线传输延时问题，设计反馈信号传输延时补偿观测器;然后，结合钢丝绳张力主动控制模型，将反步控制和障碍李雅普诺夫函数相结合设计得到控制律;最后，搭建了双绳缠绕式深井提升试验台，对提出的控制方法开展了实验验证，实验结果表明，延时补偿观测器可以有效减小由于无线传输造成的钢丝绳张力反馈信号滞后量，与传统的被动式张力调节装置相比，提出的钢丝绳张力主动控制方法可以更有效地减小两根钢丝绳之间的张力差。
1 钢丝绳张力主动控制系统建模
双绳缠绕式深井提升系统如图1所示，系统主要包括:卷筒、提升钢丝绳、浮动天轮和提升容器。双绳缠绕提升系统利用两个卷筒驱动两条钢丝绳提升一个容器，在提升和下放过程中，由于钢丝绳制造偏差、卷筒尺寸制造偏差、钢丝绳弹性变形等因素，两根钢丝绳会出现提升不同步现象，造成钢丝绳张力差。提出利用液压缸驱动浮动天轮，改变浮动天轮高度，进而主动调节垂直段提升钢丝绳长度，最终调节提升系统运行过程中两根钢丝绳张力。
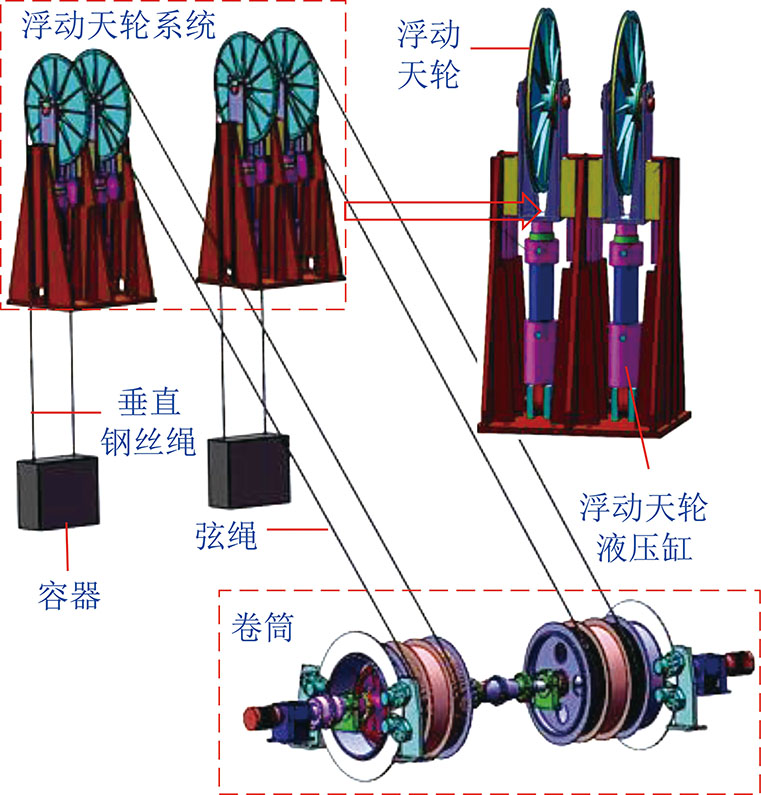
图1 双绳缠绕式深井提升系统
Fig.1 Double-rope winding deep well hoisting system
浮动天轮张力主动调节系统如图2(a)所示。对于浮动天轮系统来说，直接负载力并不是钢丝绳张力，该负载力可以通过浮动天轮和液压缸之间安装的压力传感器进行测量，通过测量的负载压力值可以对提升钢丝绳张力进行推导，液压缸所受负载压力与钢丝绳张力之间关系如图2(b)所示。由图2(b)可知，作用在浮动天轮液压缸上的负载力为垂直提升钢丝绳张力和弦绳张力的合力，通过如图2(b)所示的几何关系，垂直提升钢丝绳张力为
(1)
式中，Tl为钢丝绳张力;α为钢丝绳弦绳与水平面夹角;Fp为作用在浮动天轮液压缸上的负载力。
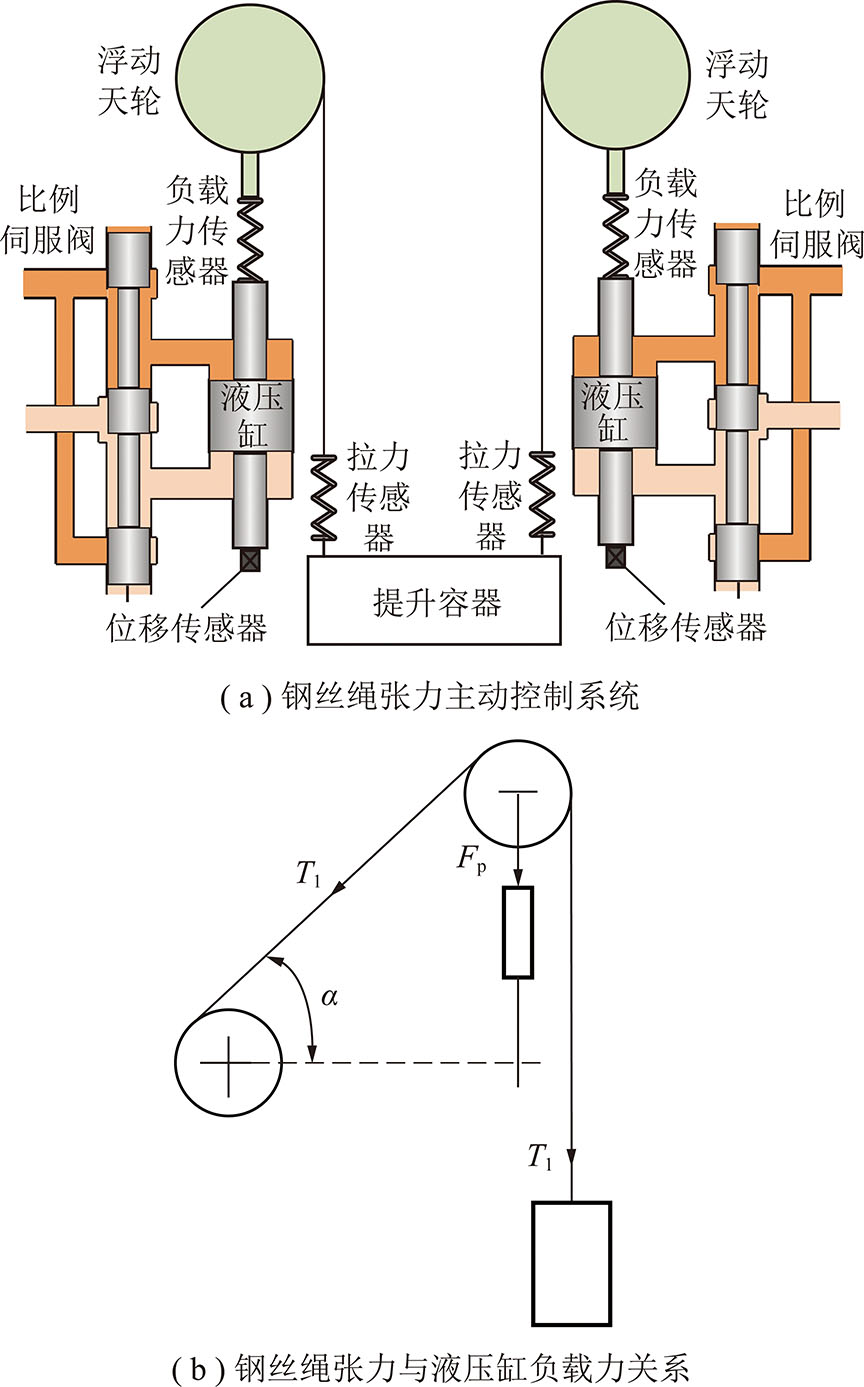
图2 钢丝绳张力主动控制原理
Fig.2 Schematic diagram of wire rope tension active control system
液压缸轴向负载力通过浮动天轮和液压缸活塞杆之间的压力传感器测量，钢丝绳张力通过钢丝绳末端与容器之间的张力传感器测量，根据式(1)所示的负载力与钢丝绳张力之间的关系，钢丝绳张力为
Tl=g(Fp)=g[kf(xp-xhs)]
(2)
式中，kf为压力传感器弹性刚度;xp为液压缸活塞杆位移;xhs为浮动天轮位移。
浮动天轮液压缸的力平衡方程为
(3)
式中，mp为浮动天轮、钢丝绳和一部分提升负载质量;Ap 为液压缸有效作用面积;PL为液压缸两压差;Bp为弹性阻尼系数;t为时间。
比例伺服阀负载流量QL为
(4)
式中，Ctp为液压缸总泄漏系数，可表示为Ctp=Cip+Cep/2，Cip为内泄漏系数，Cep为外泄漏系数;βe为液压油有效体积弹性模数;Vt为液压缸两腔总容积。
钢丝绳张力平衡系统的状态变量为
则控制系统的状态空间方程为
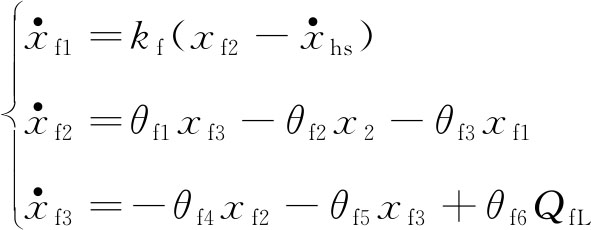
(5)
其中，各状态方程中的系数具体如下:
θf1=Ap/mp，θf2=Bp/mp，θf3=1/mp，θf4=4βeAp/Vt，θf5=4βeCtp/Vt，θf6=4βe/Vt;Qfl为钢丝绳张力平衡控制负载流量。
2 钢丝绳张力传输延时补偿观测器
在双绳缠绕式深井提升系统中，钢丝绳张力信号无法通过布置电缆的方式实时采集反馈信号，需要采用无线采集方式，然而无线采集通常存在传输延时，并不能将采集到的信号进行实时反馈，进而影响控制算法的实现，降低控制精度，甚至会导致系统不稳定。针对该问题，设计了反馈信号传输延时补偿观测器。
钢丝绳张力平衡系统可看作一个三阶非线性系统，则式(5)可改写为
Abtxbt(t)+Bbtχbt(x,t,u)
(6)
式中，
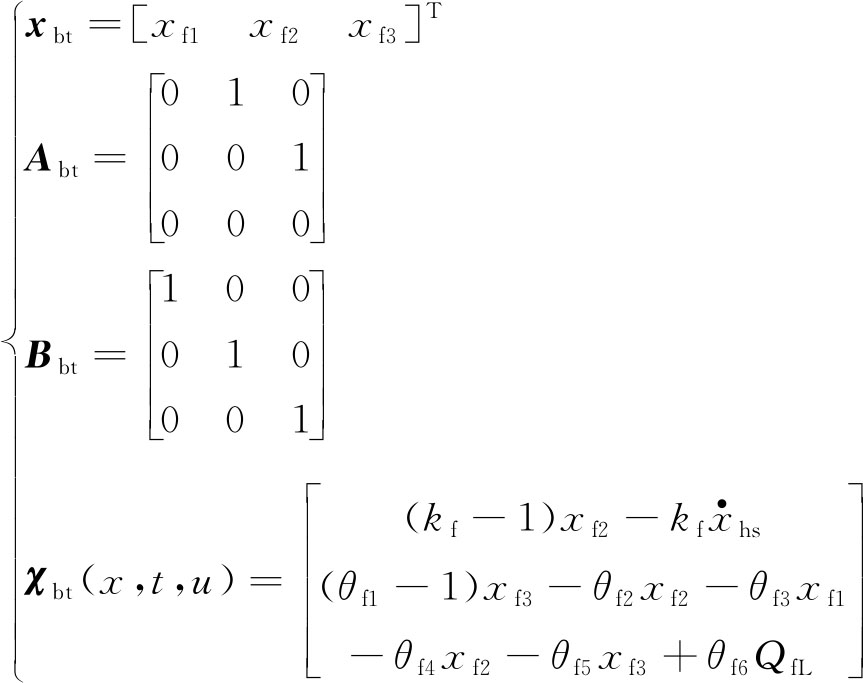
假设钢丝绳张力信号经过无线采集系统传输后的延时为Δt，则控制系统实际测量到的钢丝绳张力信号为
(7)
式中，
钢丝绳张力平衡系统状态空间方程进行转换的过程可知，2个转换后矩阵方程的系数Abt和Cbt均为已知的。因此，基于此通过设计增益矩阵
可以使矩阵Abt-KbtCbt满足Hurwitz条件。定义
为矩阵Abt-KbtCbt的特征值集合，则利用矩阵Abt-KbtCbt的特征值集合可将增益矩阵
设计为
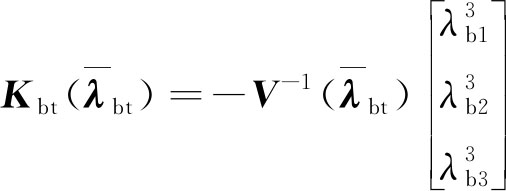
(8)
范德蒙德矩阵
定义为
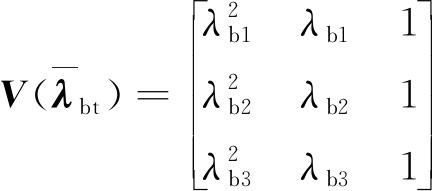
(9)
基于式(9)所示的范德蒙德矩阵，矩阵和Abt-KbtCbt可以被对角化:
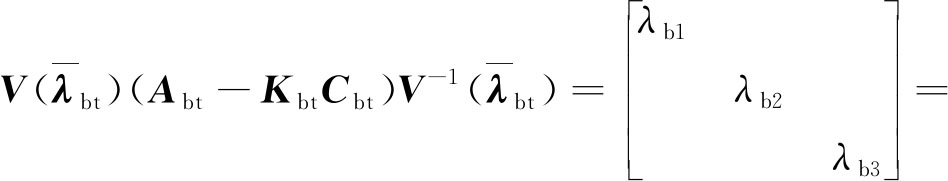
(10)
其中，
为关于
的对角矩阵。式(10)左右两边分别乘以
和
(11)
针对式(6)所示的钢丝绳张力平衡延时系统，信号传输延时观测器可以设计[19]为
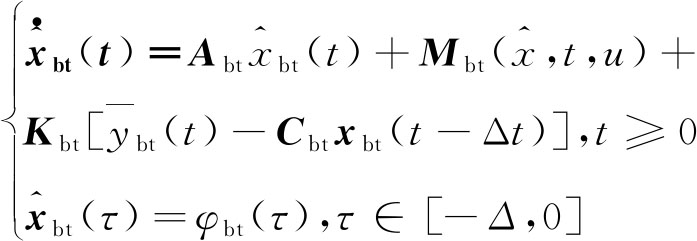
(12)
其中，
为xbt的估计值;Δ为延时上限值。
对于提升系统和钢丝绳张力平衡系统的信号传输延时补偿，考虑如下矩阵方程
(Abt-KbtCbt)TPbt+Pbt(Abt-KbtCbt)+
(13)
其中，αbt和γbt为实数;Ibt为单位矩阵;Nbt为正定的3阶对角矩阵，对于任意的正常数αbt和γbt，通过设计矩阵Kbt，存在正定的对称对角矩阵Pbt使式(13)满足等式关系。
证明:式(13)可以改写为如下形式
(14)
式中，
假设矩阵Kbt的特征值集合
中的元素满足如下条件
(15)
则可得矩阵
是具有稳定性，基于此，可得公式(14)的解为
(16)
为保证矩阵Pbt正定，在式(16)的左右两边分别乘以
和Bbt，可得
(17)
根据式(16)和(17)所示的转换关系可得
(18)
式中,
因此，式(17)可改写为
(19)
结合式(16)～(19)可得，为保证矩阵Pbt正定，应保证
为正定矩阵。由式(19)可以看出，为正定矩阵且不受Nbt的数值影响的不等式条件表示如下
(20)
由于
则可得
(21)
根据式(20)，可得
(22)
基于此，当选取λbt=-ωbt的值足够小时，式(22)满足所示关系。因此，对于任意取值的γbt，可使保持正定。
定义状态变量延时观测偏差为
(23)
结合式(6)和(12)，可得
ebt(τ)=xbt(τ)-φbt(τ),τ∈[-Δ,0]
(24)
式中，
为延时时间;
信号传输延时观测器设计完成后，应对其收敛性进行证明，本文基于Lyapunov-Razumikhin稳定性判据对观测器的收敛性进行验证，可具体描述为
(25)
因此，设计的延时观测器可保证系统稳定性。
3 钢丝绳张力主动控制方法
提出了将反步控制和障碍李雅普诺夫函数相结合的控制方法来设计钢丝绳张力控制律，障碍李亚普诺夫函数在解决非线性系统中的状态和输出约束上有较为突出的优点，当状态或者输出约束接近预定的约束界时，李亚普诺夫函数就会趋于无穷大，保证了在系统运动过程中约束限制被破坏的可能[20]。
图3为钢丝绳张力主动控制原理图，钢丝绳张力反馈值经过延时观测器处理后，结合基于障碍李雅普诺夫函数的反步控制器，得到浮动天轮液压缸的驱动电压值，驱动浮动天轮液压缸对钢丝绳张力进行主动调节。对两根钢丝绳施加相同的张力参考信号，从而减小两根钢丝绳之间的张力差。
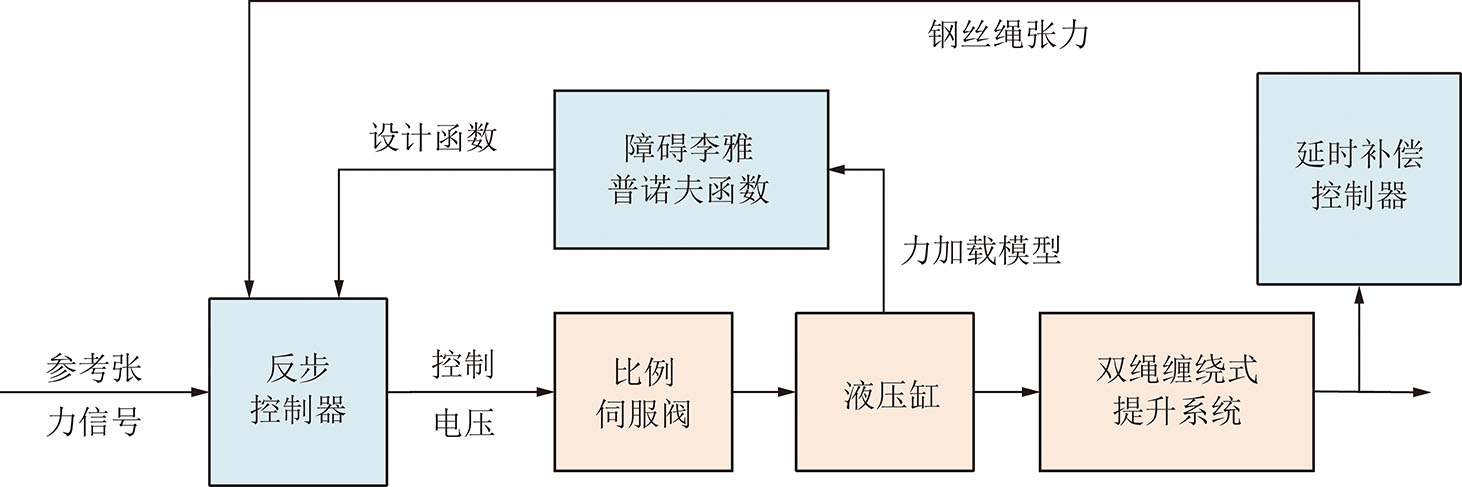
图3 钢丝绳张力主动控制原理
Fig.3 Principle diagram of wire rope tension active control
具体设计步骤包括以下3步:
(1)定义钢丝绳张力跟踪误差为ef1
ef1=xf1-xf1r
(26)
式中，xf1r为钢丝绳张力的期望值。
钢丝绳张力跟踪误差关于时间的导数
(27)
然后，定义系统状态变量xf2的虚拟控制变量为αf1，则状态变量xf2与其虚拟控制变量αf1之间的偏差为
ef2=xf2-αf1
(28)
则状态变量xf2为
xf2=ef2+αf1
(29)
定义关于误差ef1的障碍Lyapunov函数Vf1为
(30)
式中，ka为控制参数。
则Vf1关于时间的导数为
(31)
虚拟控制变量αf1为
(32)
则Vf1关于时间的导数改写为
(33)
(2)定义状态变量xf3的虚拟控制变量为αf2，则状态变量xf3与其虚拟控制变量αf2之间的偏差为
ef3=xf3-αf2
(34)
虚拟控制变量αf1的时间导数为
(35)
偏差ef2的时间导数为
(36)
然后，定义关于误差ef2的障碍Lyapunov函数Vf2
(37)
则Vf2关于时间的导数为
(38)
虚拟控制变量αf2为
(39)
则Vf2关于时间的导数改写为
(40)
(3)在该设计步骤中，由于实际控制输入QfL是可见的，因此不需要再定义虚拟控制变量，则虚拟控制变量αf2的时间导数为
Aθf2+Bθf3+C
(41)
式中，
偏差ef3的时间导数为
Aθf2+Bθf3+C
(42)
然后，定义关于偏差ef3和参数估计误差的Lyapunov函数Vf3，即
(43)
则Vf3关于时间的导数为
(44)
然后，实际控制输入QfL可设计为
(45)
则Vf3关于时间的导数可改写为
(46)
因此，系统稳定性可证。
4 实验结果及分析
为验证本文提出的钢丝绳张力主动控制方法的有效性，在中信重工机械股份有限公司搭建的双绳缠绕式深井提升试验台上开展了试验验证(图4)，试验台具体参数见表1。
图4 双绳缠绕式深井提升试验台
Fig.4 Double-rope winding deep well hoisting experimental system
表1 双绳缠绕式深井提升试验台参数配置
Table 1 Parameters of double-rope winding deep well hoisting experimental system
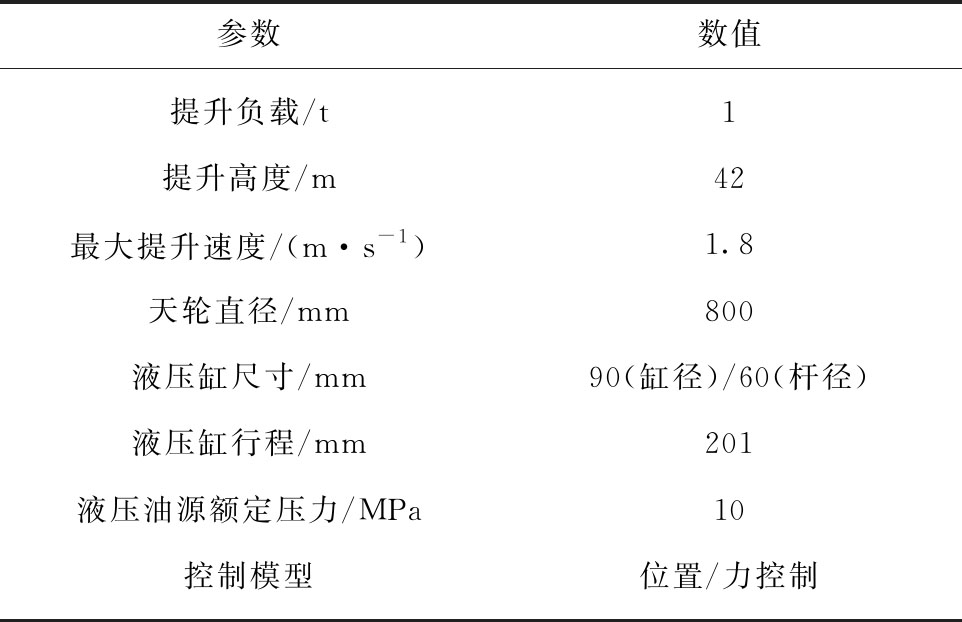
参数数值提升负载/t1提升高度/m42最大提升速度/(m·s-1)1.8天轮直径/mm800液压缸尺寸/mm90(缸径)/60(杆径)液压缸行程/mm201液压油源额定压力/MPa10控制模型位置/力控制
双绳缠绕式深井提升试验系统控制方案如图5所示。钢丝绳张力主动控制系统由4套伺服液压缸及4套比例伺服阀组成，每个液压缸均安装有位移传感器、油压传感器以及负载力传感器。钢丝绳张力反馈信号由串联在钢丝绳和提升容器之间的拉力传感器获得后传递至无线采集系统。各传感器反馈值经信号调理系统处理后由研华公司A/D板卡PCI-1716采集。各数字量信号由PCL-731采集。两根钢丝绳张力差信号经控制算法处理后产生浮动天轮期望的位移信号，生成的位移信号与液压缸的位移输出信号构成位置闭环，进而由凌华公司D/A板卡ACL-6126生成±10 V范围内的电压信号，经信号调理模块优化处理后驱动比例换向阀的工作，比例换向阀根据期望的激励信号控制液压油输入到液压缸中，液压缸驱动浮动天轮将按照期望的位移信号沿导轨运动。
图5 双绳缠绕式深井提升试验系统控制方案
Fig.5 Control scheme of double-rope winding deep well hoisting experimental system
图6为钢丝绳张力平衡系统使用延时观测器前后两根钢丝绳张力反馈值比较，从图中可以看出使用延时观测器可以有效减小反馈延时和控制信号延时造成的钢丝绳张力相位差。
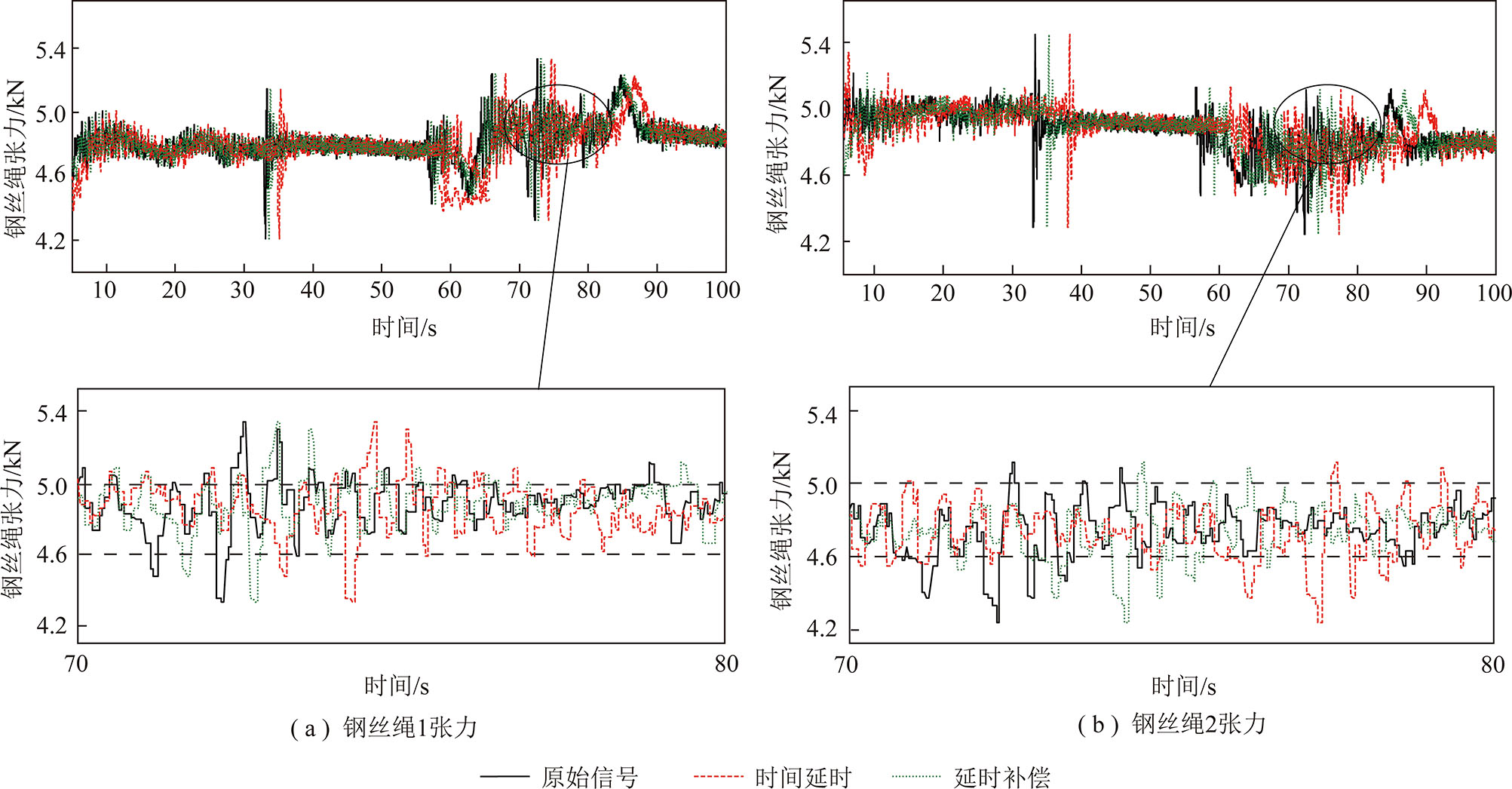
图6 钢丝绳张力延时补偿效果
Fig.6 Effect of delay compensation on two wire rope tensions
为验证提出的主动控制方法相对于被动控制的优越性，分别在0.5，1.0，1.4 m/s三种运行速度下使用不同控制方法进行了实验(图7～9)。对于主动控制方法，延时补偿观测器和钢丝绳张力平衡控制器的控制参数见表2。
图10为3种运行速度下不同控制方法所得的钢丝绳张力差。由图7～10可知，无论在高速还是低速工况下，采用主动式液压缸浮动天轮钢丝绳张力调节模型可以更有效地减小两根钢丝绳之间的张力差异。
表2 控制器参数
Table 2 Parameters of controllers
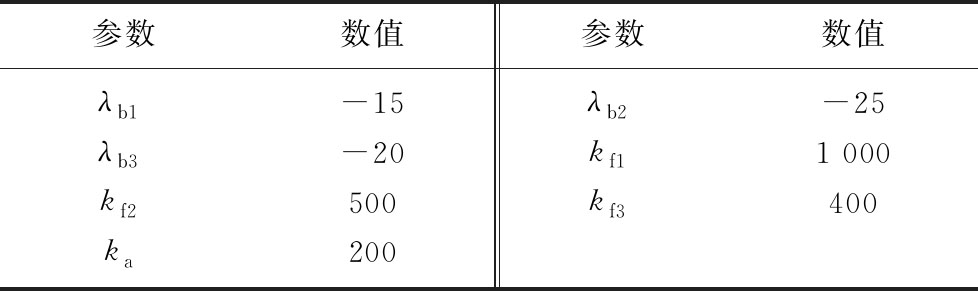
参数数值参数数值λb1-15λb2-25λb3-20kf11 000kf2500kf3400ka200
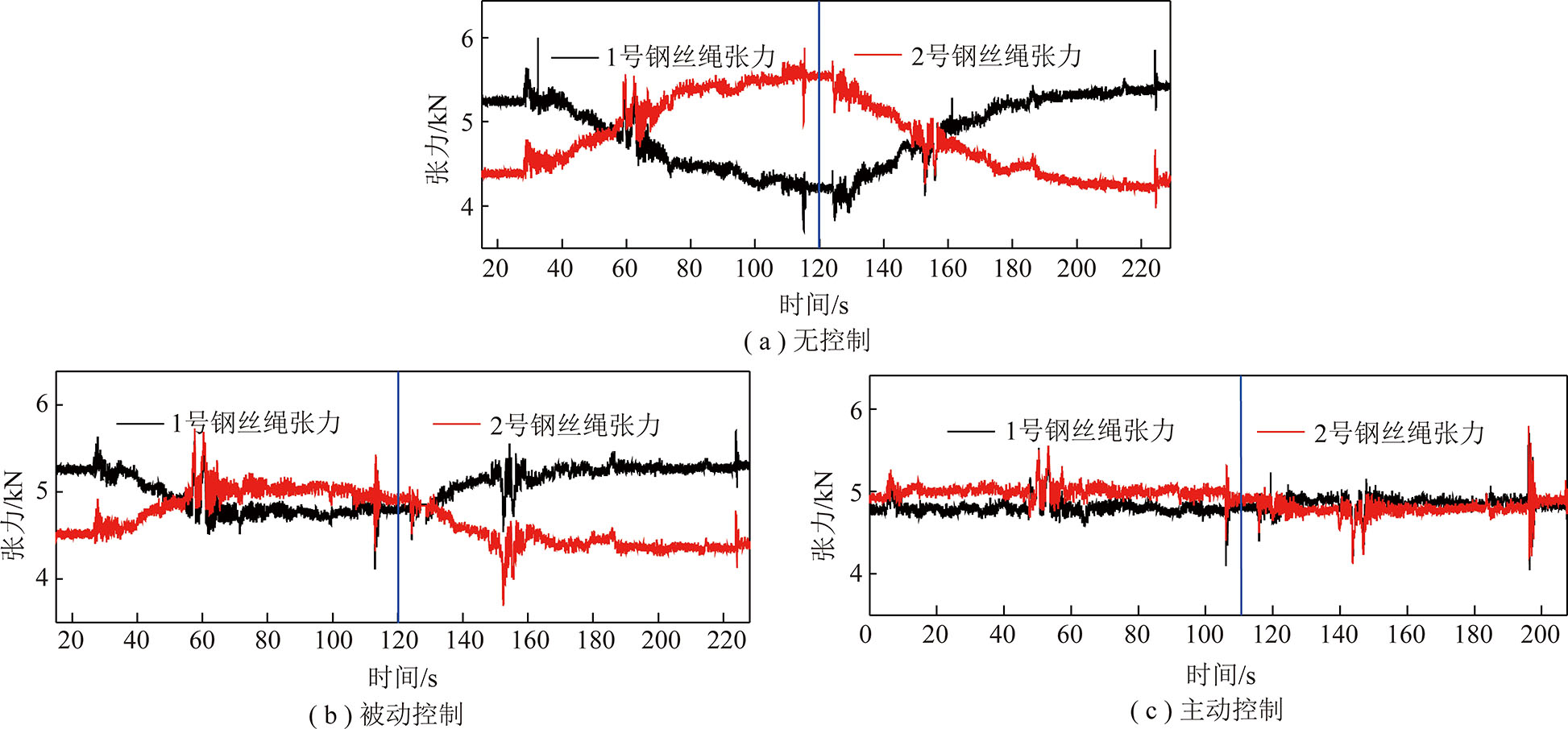
图7 运行速度0.5 m/s的钢丝绳张力控制结果
Fig.7 Results of wire rope tension control with operating speed of 0.5 m/s
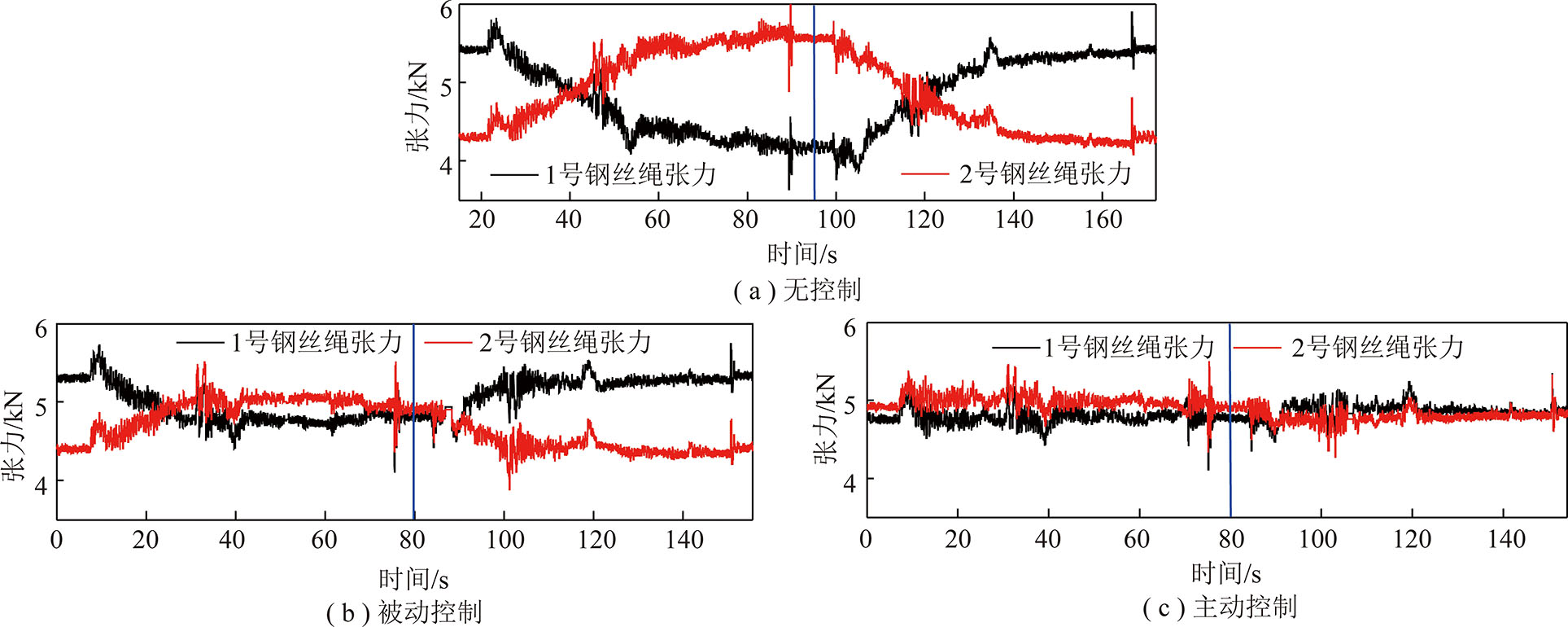
图8 运行速度1.0 m/s的钢丝绳张力控制结果
Fig.8 Results of wire rope tension control with operating speed of 1.0 m/s
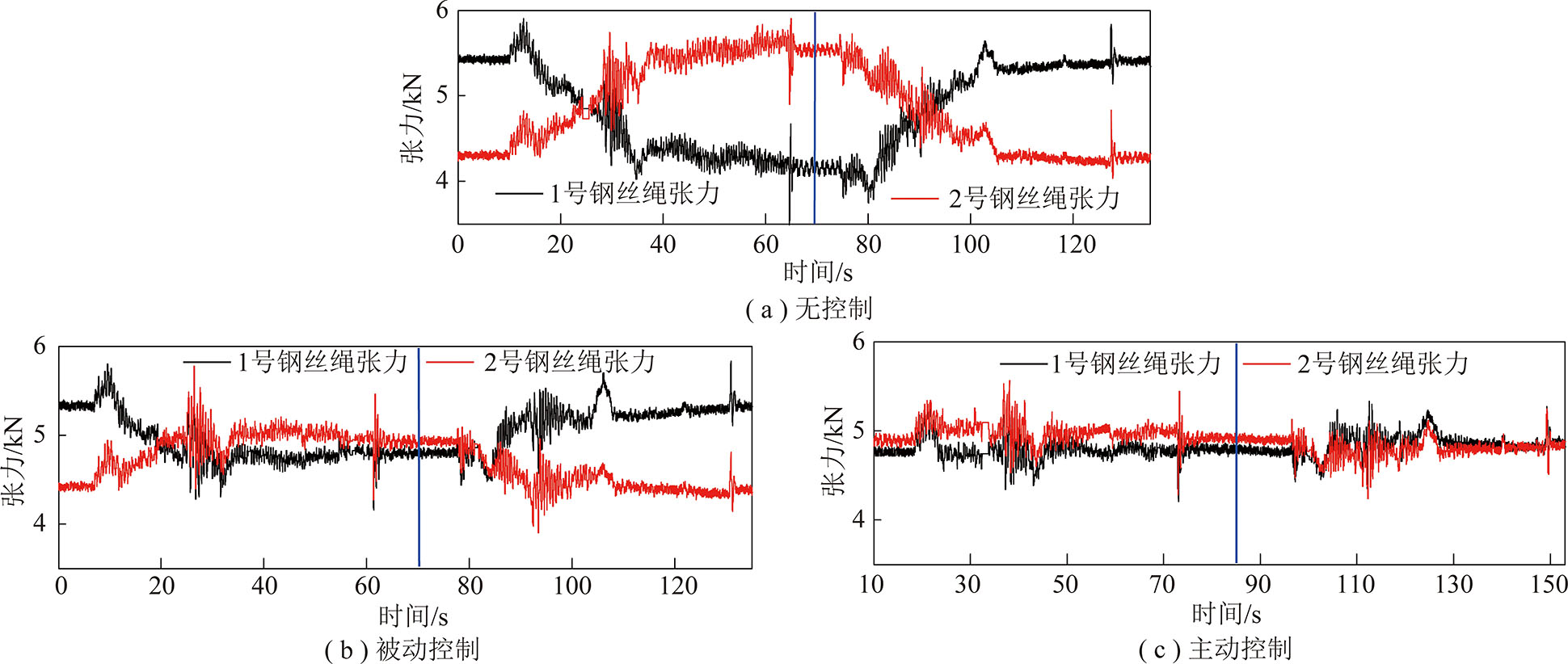
图9 运行速度1.4 m/s的钢丝绳张力控制结果
Fig.9 Results of wire rope tension control with operating speed of 1.4 m/s
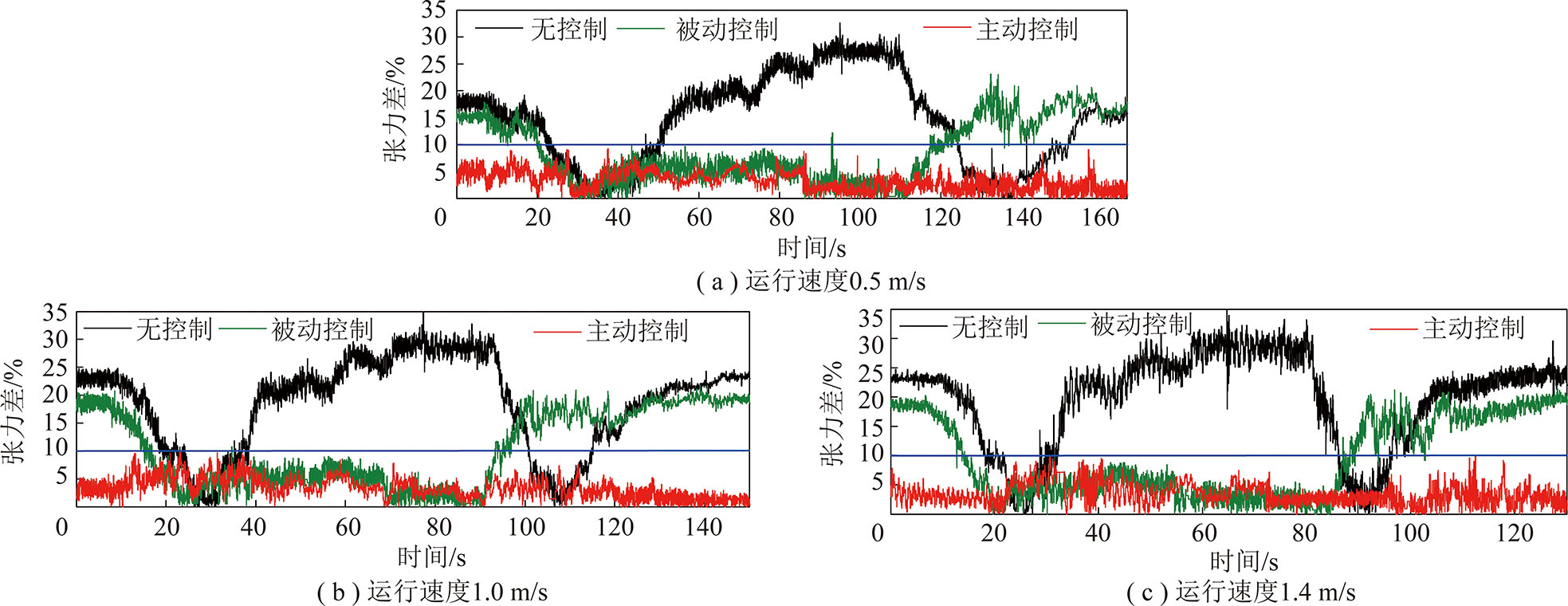
图10 不同运行速度下的钢丝绳张力差
Fig.10 Difference of wire rope tension at different operating speeds
5 结 论
(1)分析了双绳缠绕式深井提升系统钢丝绳张力主动控制原理，建立了控制模型，并在此基础考虑提升系统运行过程中钢丝绳张力反馈信号通过无线传输存在延时问题，设计了针对反馈信号传输延时的补偿观测器，并对加入延时补偿观测器之后系统的稳定性进行了证明。
(2)将障碍李雅普诺夫函数与反步控制相结合，设计了双绳缠绕式深井提升系统钢丝绳张力主动控制方法，并在试验台上对提出的延时补偿和钢丝绳张力控制方法进行了试验验证。
[1] 刘劲军,邹声勇,张步斌,等.我国大型千米深井提升机械的发展趋势[J].矿山机械,2012,40(7):1-6.
LIU Jinjun,ZOU Shengyong,ZHANG Bubin,et al.Discussion trend of domestic large hoisting equipments for deep shafts of thousands meters[J].Mining & Processing Equipment,2012,40(7):1-6.
[2] ALFRED C.Mine hoisting in deep shafts in the 1st half of 21st Century[J].Acta Montanistica Slovaca,2002,7(3):188-192.
[3] 吴荣华.立井摩擦提升钢丝绳张力平衡动态特性及优化研究[D].徐州:中国矿业大学,2014.
WU Ronghua.Dynamic characteristics and optimization of hoisting frictional rope’s tension balance[D].Xuzhou:China University of Mining and Technology,2014.
[4] YAO J N,XIAO X M,PENG A H,et al.Assessment of safety for axial fluctuations of head sheaves in mine hoist based on coupled dynamic model[J].Engineering Failure Analysis,2015,51:98-107.
[5] 桑安乐.多绳提升机钢丝绳张力自动平衡悬挂装置的使用探讨[J].中国科技信息,2007,16:37-38.
SANG Anle.Application of automatic balance suspension device for wire rope tension of multi-rope hoist[J].China Science and Technology Information,2007,16:37-38.
[6] 邵杏国,朱真才,曹国华,等.吊盘稳车机构调平控制策略研究与实验验证[J].煤炭学报,2012,37(3):528-532.
SHAO Xingguo，ZHU Zhencai，CAO Guohua,et al.Auto-leveling control for sinking winch mechanism and experimental validation[J].Journal of China Coal Society,2012,37(3):528-532.
[7] MAHIR H,AMIR K.Optimization of actuator forces in cable-based parallel manipulators using convex analysis[J].IEEE Transactions on Robotics,2008,24(3):736-740.
[8] ASTR M K J,WITTENMARK B.Adaptive control[M].New York:Courier Dover Publications,2008.
[9] SASTRY S,BODSON M.Adaptive control:Stability,convergence and robustness[M].New York:Dover Publications,2011.
[10] 张细政,王耀南.永磁同步电机鲁棒自适应反步控制[J].煤炭学报,2009,34(4):572-576.
ZHANG Xizheng,WANG Yaonan.Adaptive backstepping based robust speed control of permanent magnet synchronous motor servo drive[J].Journal of China Coal Society,2009,34(4):572-576.
[11] 闫茂德,贺昱曜,李俊.一类三角结构非线性系统状态参考反演变结构控制[J].火力与指挥控制,2008,33(3):13-16.
YAN Maode,HE Yuyao,LI Jun.State reference backstepping variable structure control for a class of nonlinear systems with uncertainties[J].Fire Control and Command Control,2008,33(3):13-16.
[12] 吴江潦,易灵芝,彭寒梅,等.开关磁阻电机自适应模糊神经网络系统(ANFIS)无位置传感器控制[J].煤炭学报,2010,35(8):1401-1405.
WU Jiangliao,YI Lingzhi,PENG Hanmei,et al.Position sensorless control of the switched reluctance motor using adaptive network fuzzy inference system(ANFIS)[J].Journal of China Coal Society,2010,35(8):1401-1405.
[13] TONG S C,LI C Y,LI Y M.Fuzzy adaptive observer backstepping control for MIMO nonlinear systems[J].Fuzzy Sets and Systems,2009,160(19):2755-2775.
[14] TONG S C,LIU C L,LI Y M.Fuzzy adaptive decentralized control for large-scale nonlinear systems with dynamical uncertainties[J].IEEE Transactions on Fuzzy Systems,2010,18(5):845-861.
[15] ZHU Z C,LI X,SHEN G,et al.Wire rope tension control of hoisting systems using a robust nonlinear adaptive backstepping control scheme[J].ISA Transactions,2018,72:256-272.
[16] 孙萍.基于反步控制的电液伺服系统输出约束问题研究[D].成都:电子科技大学,2018.
SUN Ping,Backstepping control of electro-hydraulic servo system with output constraints[D].Chengdu:University of Electronic Science and Technology of China,2018.
[17] TEE K,GE S S,TAY E.Barrier Lyapunov Functions for the control of output-constrained nonlinear systems[J].Automatica,2009,45(1):918-927.
[18] REN B,GE S S,TEE K P,et al.Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function[J].IEEE Transactions on Neural Networks,2010,21(8):1339-1345.
[19] CACACE F,GERMANI A,MANES C.An observer for a class of nonlinear systems with time varying observation delay[J].Systems & Control Letters,2010,59(5):305-312.
[20] GUO Q,ZHANG Y,CELLER B G,et al.State-constrained control of single-rod electrohydraulic actuator with parametric uncertainty and load disturbance[J].IEEE Transactions on Control Systems Technology,2018,26(6):1-8.
