在大部分深部开采矿井,围岩剧烈变形已成为采动巷道的常态,甚至冒顶事故也时有发生,已严重影响矿山的正常生产,威胁矿井安全。深部巷道开挖后,围岩因卸荷作用而产生大范围破坏,无论是高强度锚杆(索)支护还是其他支护方式似乎都难以阻止巷道围岩的破坏。研究表明,锚杆支护难以改变巷道的塑性区和应力场分布,并且在目前的技术装备条件下,任何支护方式均难以有效控制高应力带给巷道围岩的给定变形[1-5],那么,锚杆支护能在多大程度上控制巷道围岩的大变形?巷道的支护问题如何解决?这都是深部巷道支护必须深入研究的重要问题。
近年来,国内外学者大多在利用数值模拟方法、试验方法研究锚杆支护对锚固体的峰值强度、残余强度、内部应力变化的影响以及试件破坏规律等方面,但研究对象多集中在峰前完整岩体或预制裂隙试件。例如,侯朝炯[6]通过相似材料试验,研究了锚杆支护对岩体峰值强度和残余强度等力学参数的强化作用。孟波[7]通过真三轴相似模拟试验,研究了破裂围岩锚固体以及锚杆的变形破坏特征。董方庭[8]通过井下碎石锚固模拟试验研究了单根锚杆的控制范围、锚固体强度以及内应力分布情况。李术才[9]研究了复杂应力状态下脆性断续节理岩体在压剪、拉剪应力状态下的本构模型及断裂损伤机制。王平[10]通过对预制裂隙试件进行单轴破断试验研究了锚杆对裂隙岩体的锚固机制及影响因素。上述研究多集中在完整岩体试件或预制裂隙的试件,巷道开挖后,围岩在高地应力作用下发生破裂形成塑性区,塑性区内围岩的裂隙均为无规则裂隙,但阐述有关锚杆对塑性区内破裂围岩的锚固作用研究的文献较少见[11-15]。
事实上,对于深部巷道,支护对象往往是峰后破裂围岩,研究锚杆对峰后破裂围岩的控制作用,需要在实验室对试件进行人为预裂。笔者采用自制的三轴相似模拟试验台进行了预裂试件的锚固试验,通过对锚固试件的破坏特征进行分析,研究锚杆对破裂岩体的锚固作用,得到一些有益的结论,对揭示锚杆支护机理、深部巷道变形控制有重要的借鉴意义。
1 试验装置与方案
1.1 试验装置
巷道开挖前,围岩体处于原岩应力状态,巷道开挖后,其围岩弹性能瞬间释放导致周边围岩发生塑性破坏,形成一定范围的塑性区;此时对巷道围岩进行支护,锚杆作用范围为处于塑性破坏状态的岩体,其蠕变特性使得锚杆与围岩形成的锚固体力学特性不断发生变化,而力学解析方法难以有效的研究该问题,即使获得了力学解析解,但由于与实际条件差别较大,其研究成果也难以应用于工程实践,而相似模拟方法是一种较为有效的研究手段。
为了研究锚杆对破裂试件的锚固效果,制作了一套能够模拟现场围岩应力情况的三轴加载试验装置,如图1所示,其左右侧约束挡板由2块80 mm厚的Q235钢板制作而成,并通过φ50 mm的Q235圆钢制作而成的拉杆连接;后部挡板为厚度80 mm的 Q235钢板,由焊接在左右侧挡板上的限位条约束,后档板上布置有锚杆孔位;实验室现有压力试验机的底座尺寸为900 mm×600 mm,除去装置两侧约束挡板占用的空间,此装置只能容纳的试件尺寸为400 mm×400 mm×400 mm。试件顶部传力板采用多层钢板叠合焊制而成,为了防止传力板与周围挡板间相互接触咬合的问题,其尺寸设置为395 mm×395 mm。前挡板位置设有反力板,用于给试件施加前端围压,反力板由套在水平拉杆上的反力套环固定,千斤顶放置于反力板与前挡板之间,通过反力板给前档板施加围压来模拟原岩应力状态,卸除前挡板围压能够模拟开挖过程,施加锚杆能够模拟锚杆的锚固作用。试验装置的刚度均满足试验要求。
1.2 模拟试验相似关系及试验材料
水泥砂浆材料是一种力学性质与岩石相似的非均质相似材料,可以较真实的模拟岩石材料[16]。本文采用的相似材料为石英砂、水泥、石膏按一定的质量比例加水配合而成,质量比例为75%∶10%∶15%,水占固体质量的10%,根据力学试验获得其容重为17 kN/m3,采用该配比来模拟巷道围岩中常见的砂质泥岩。
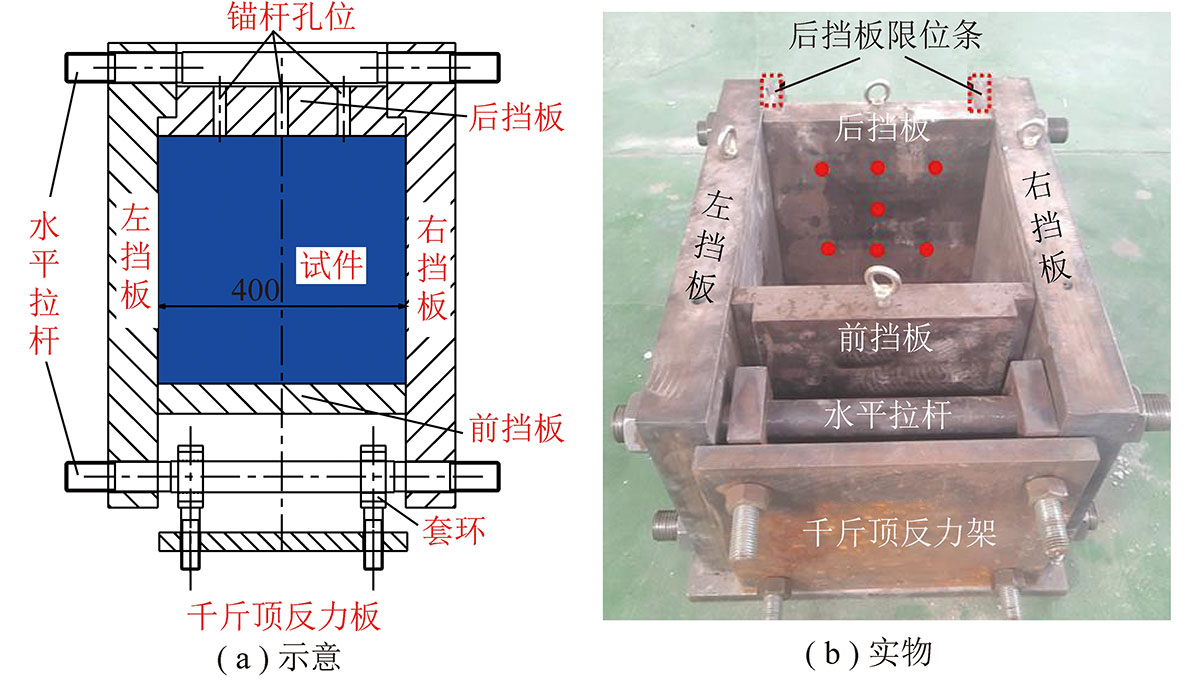
图1 模型试验台
Fig.1 Model test device
考虑到现场锚杆直径、钻孔直径、锚固力均较小,煤矿现场的锚杆支护间排距一般为800 mm×800 mm左右,因此几何相似比确定为2,砂质泥岩的容重为24 kN/m3,故容重比为1.4,则应力相似比Cσ=ClCγ=2.8,弹性模量、黏结力的相似比均为2.8,预紧力相似比![]() 泊松比、内摩擦角以及应变的相似比均为1[17]。经过换算及试验,相似锚杆采用φ8 mm HRB400螺纹钢,采用扭矩扳手对锚杆施加一定的预紧力,锚杆上粘贴应变片用于测试锚杆受力情况;锚杆托盘选用φ70 mm厚度10 mm的圆形钢板。试件原型及模型物理力学参数见表1。
泊松比、内摩擦角以及应变的相似比均为1[17]。经过换算及试验,相似锚杆采用φ8 mm HRB400螺纹钢,采用扭矩扳手对锚杆施加一定的预紧力,锚杆上粘贴应变片用于测试锚杆受力情况;锚杆托盘选用φ70 mm厚度10 mm的圆形钢板。试件原型及模型物理力学参数见表1。
表1 试件与原型物理力学参数
Table 1 Mechanical parameters of physical specimens and prototype
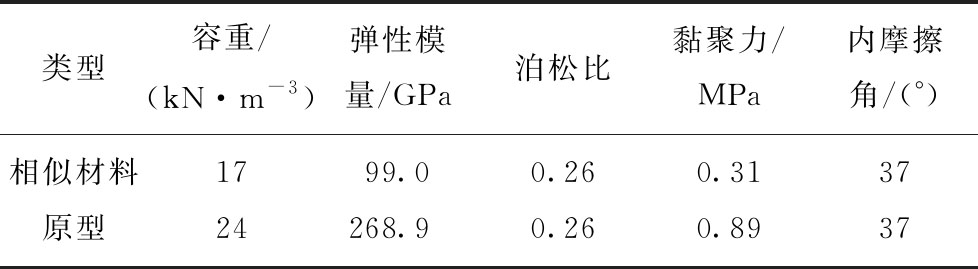
类型容重/(kN·m-3)弹性模量/GPa泊松比黏聚力/MPa内摩擦角/(°)相似材料1799.00.260.3137原型24268.90.260.8937
按照配比将材料充分搅拌后,在试件模具中浇筑成型,为尽量减小试件之间的力学性能差异,同一组试验采用搅拌机配料一次制作若干个试件,如图2所示。为减小试件与模型试验台间的摩擦作用,在试件与试验台装置间缠裹塑料薄膜,截取薄膜尺寸分别为400 mm×400 mm,400 mm×3 200 mm,其中400 mm×400 mm薄膜放置于试件底部与顶部,分别减小试件底部与底座间的摩擦以及试件与试验机压头之间的摩擦,而400 mm×3 200 mm缠绕于试件四周,减小试件与周围钢板间的摩擦,然后将试件放置于模型试验台中。

图2 试件
Fig.2 Specimen
1.3 试验方案与过程
锚杆提供的支护阻力与原岩应力相差1~2个数量级,而与破碎围岩中的残余应力同处一个数量级,因此锚杆对破裂围岩的支护效果更为明显;巷道开挖后,在锚杆支护前,围岩弹性能的释放引起围岩发生破坏形成塑性区,锚杆的支护对象是塑性区破裂围岩。因此,对试件进行预裂,制作峰后破裂围岩。
预裂的步骤如下:安装试件后,将拉杆螺母拧紧,拉杆属于被动承载,当垂直方向施加载荷(第1主应力)引起试件垂直方向出现压缩变形,而试件侧向出现的膨胀变形对侧板产生作用力,同时侧板对试件存在一个反作用力,此作用力看作是第2主应力。千斤顶通过反力架对试件前挡板提供围压(第3主应力),其数值随试验机施加的垂直载荷增大而增大,以此来模拟开挖前的原岩应力状态,如图3所示。

图3 试件预裂及模型试验台
Fig.3 Specimen pre-cracking and model test device
通过施加三向压力模拟原岩应力环境,达到预定载荷后稳定一段时间,然后卸载前挡板压力,同时垂直方向持续加载,来模拟开挖卸荷作用,当试件进入峰后残余强度阶段后停止加载,此时试件预裂完成,预裂应力应变曲线如图4所示。在完成预裂的试件上安装模拟锚杆,如图5所示。采用静态应变测试仪记录加载过程中试件内部、锚杆、水平拉杆所受载荷,采用50 mm量程数显百分表配合采集卡监测和实时记录数据,如图6所示。
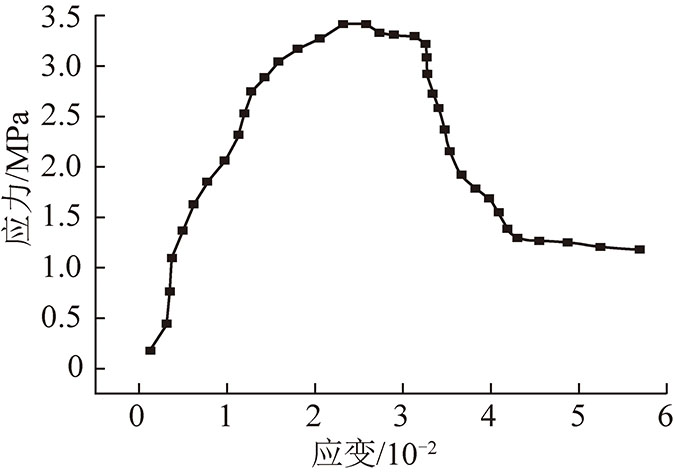
图4 预裂试件应力-应变曲线
Fig.4 Stress-stain curve of pre-splitting rock mass

图5 施加预紧力
Fig.5 Application of pre-tension

图6 模型试验台
Fig.6 Testing device
在煤矿现场,锚杆支护密度的规范表述方式是采用锚杆间排距参数,在该试验中,试件尺寸相同,均匀布置不同数量的锚杆,锚杆支护密度采用锚杆数量的表述方式更直观,因此本文采用锚杆支护数量来表达锚杆支护密度。具体试验方案如下:对于不同锚杆支护密度试验,4个试件安装不同数量的锚杆,分别为不安装锚杆、安装1根、2根、3根锚杆,锚杆预紧力均设置为5 kN;对于不同预紧力锚杆试验,均安设一根锚杆,分别施加1,5,10 kN预紧力。
2 试验结果分析
2.1 锚固体力学特性
2.1.1 锚杆支护密度的影响
预裂后试件压缩过程中垂向应力应变关系如图7所示。
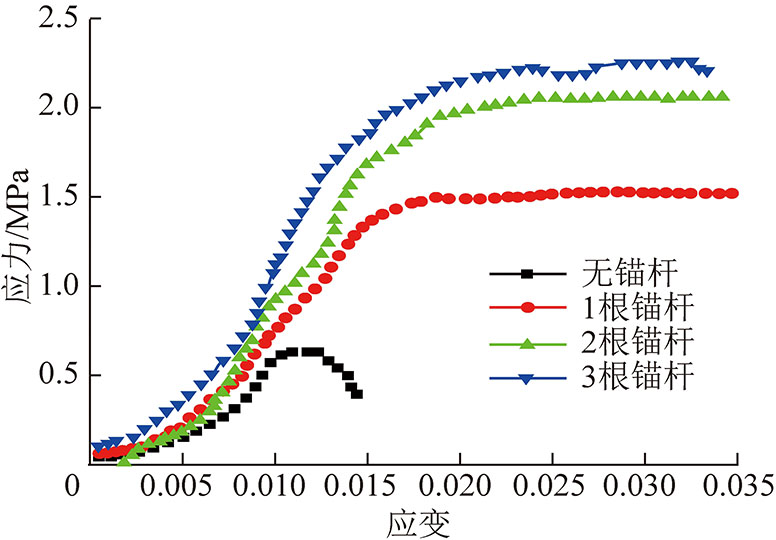
图7 试件应力应变曲线
Fig.7 Stress-strain curves of specimen
由图7分析可知,随锚杆支护密度增加,试件峰值强度表现出逐渐增大的趋势,例如当锚杆数量由1根增加到2根时,峰值强度由1.5 MPa增大到2.18 MPa,锚杆数量与试件峰值强度的关系如图8所示,试验发现,试验峰值强度与锚杆数量服从指数关系,拟合方程为
σm=-2.33e-0.49n+2.94
(1)
式中,σm为试件峰值强度;n为锚杆支护数量。
相关系数R2=0.998 6,拟合程度较高。试件不安装锚杆时,试件呈现脆性破坏;安装锚杆后,应力应变曲线具有较好的屈服平台,峰后阶段出现较大的塑性流动现象,甚至出现应变硬化特征,呈近似的理想弹塑性特征,锚固试件在发生变形的同时还能保持较高的承载能力。随着垂向载荷增大,试件发生破裂,破裂岩体发生碎胀扩容,锚杆因被动承载力对试件形成了较高的约束反力,等效于对试件施加了一定的围压,提高了试件峰值强度,限制了围岩的碎胀变形。对于深部巷道,围岩发生大变形几乎是不可避免的,但巷道围岩进行锚杆支护后,虽出现大变形,但围岩仍然保持一定的强度,这就很好的解释了深部巷道在有效的支护条件下即使出现大变形现象,但围岩仍然能保持较好的稳定性。

图8 锚杆数量与试件峰值强度的关系
Fig.8 Relationship between bolt density and peak intensity
2.1.2 预紧力的影响
设计的锚杆预紧力分别为1,5,10 kN。各预紧力下的试件峰值强度如图9所示,由图9可以看出,锚杆预紧力对试件峰值强度影响明显,呈现正相关关系。当预紧力从1 kN增大到5 kN时,对应的试件峰值强度从0.83 MPa增大到1.52 MPa,峰值强度提高83.1%;当预紧力从5 kN 提高到10 kN时,对应的峰值强度从1.52 MPa提高到1.88 MPa,峰值强度提高23.2%,说明提高锚杆预紧力,能够提高锚固体的承载能力,当锚杆预紧力比较低时,预紧力对锚固体峰值强度影响较大,当预紧力增大到一定程度后,对试件的峰值强度的影响变弱。
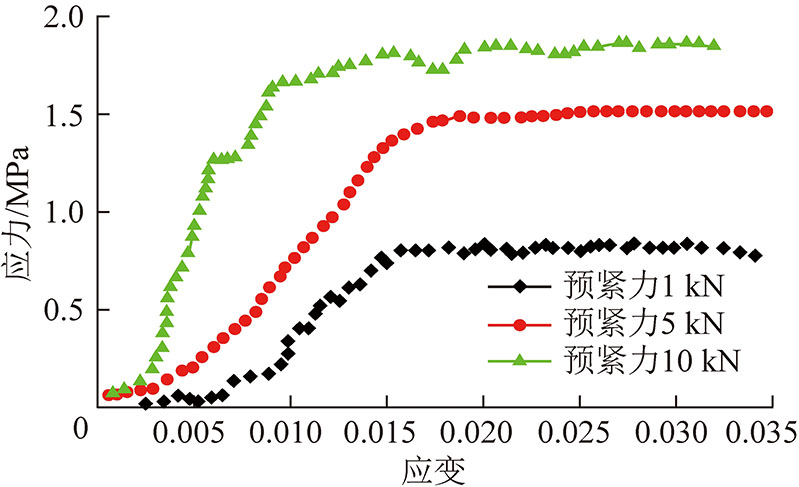
图9 不同预紧力下锚固体应力-应变曲线
Fig.9 Stress-strain curves under different pretension
2.2 变形破坏特征
试验结果发现,在试件沿垂向的位移量(压缩)均在20 mm左右时的情况下,锚杆支护密度不同,试件沿锚杆轴向的位移(拉伸)呈一定规律变化,如图10所示,当锚杆支护密度由无增大到1根时,试件沿锚杆轴向的位移由42.73 mm降低至31.56 mm,降低幅度为26.14%;当锚杆支护密度从1根增大到2根时,试件垂直位移由31.56 mm降低到27.46 mm,降低幅度为12.9%,当锚杆支护数量从2根增大到3根时,试件轴向位移为25.1 mm,降低幅度为8.69%。
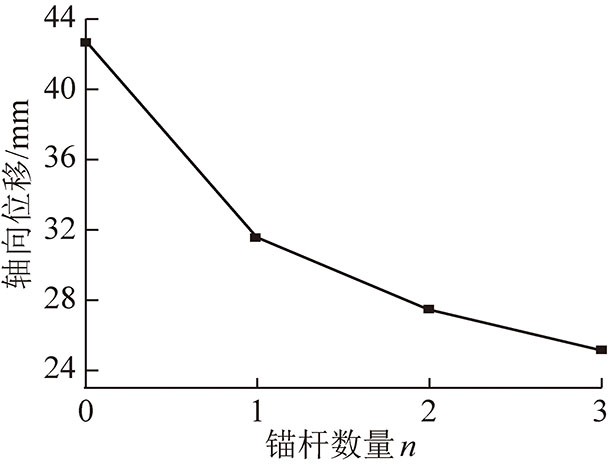
图10 不同锚杆支护密度下试件轴向位移量
Fig.10 Axial displacement of specimens under different bolt density
施加一根锚杆的试件在垂直位移量均在20 mm左右时的情况下,当锚杆施加不同的预紧力时,试件沿锚杆轴向位移呈一定规律变化,如图11所示。当预紧力由1 kN变为5 kN时,试件垂直位移由35.7 mm降低到27.2 mm,降幅为22.6%;当预紧力由5 kN增大到10 kN时,试件垂直位移由27.2 mm增大到24.5 mm,降幅为11.3%。
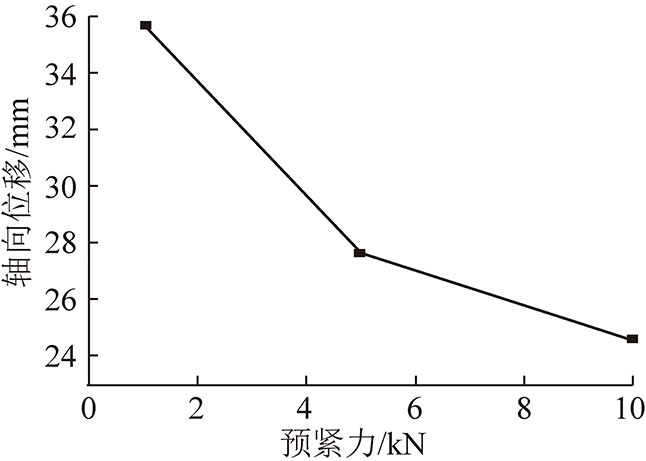
图11 不同预紧力下的轴向位移量
Fig.11 Axial displacement under different pretension
试件的体应变ε计算公式[16]为
ε=ε1+ε2+ε3
(2)
![]()
(3)
![]()
(4)
将式(3),(4)代入式(2)中,得到体应变
![]()
(5)
其中,ε1为试件垂直应变;ε2为锚杆径向方向的试件应变,近似等于0;ε3为试件临空面方向的应变;b为试件垂向压缩位移量;c为试件临空面方向的位移量;m为试件的边长,为常数。各工况情况下的体应变见表2,3。
试件无锚杆支护时,其裂纹以拉伸裂纹为主,而试件两侧及后面受到刚性挡板约束的作用,试件位移只能沿临空面方向以及垂直方向发展。在垂向位移较为接近的情况下,沿锚杆轴向位移的大小则决定了试件体应变的大小。由表2,3中可以看出,随锚杆支护密度及施加的预紧力增大,试件的体应变均出现降低,对应的试件非连续变形也会降低。
表2 不同锚杆支护密度下的位移量
Table 2 Displacement under different bolt density
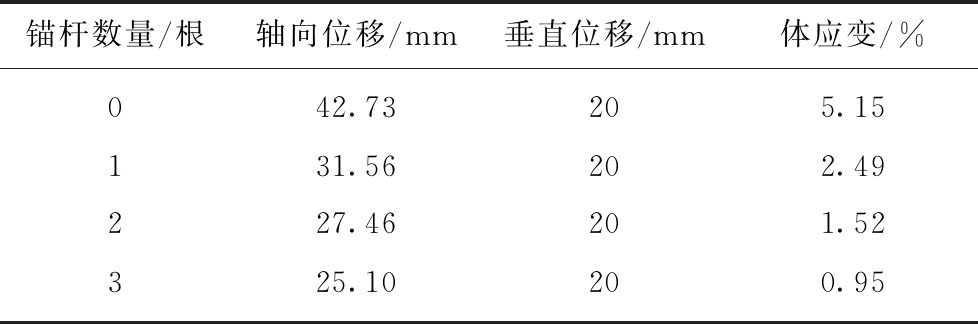
锚杆数量/根轴向位移/mm垂直位移/mm体应变/%042.73205.15131.56202.49227.4620 1.52325.10200.95
表3 不同预紧力下的位移量
Table 3 Displacement under different pretension
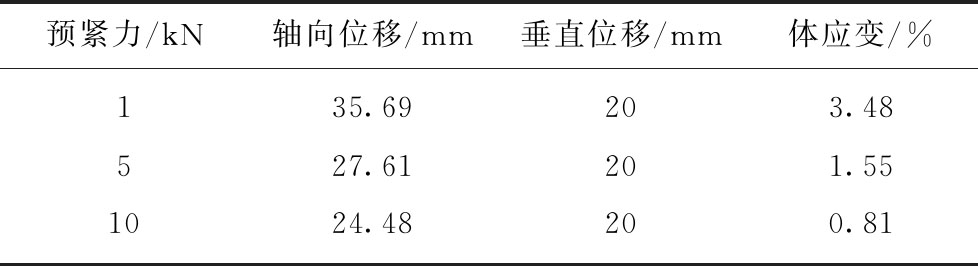
预紧力/kN轴向位移/mm垂直位移/mm体应变/%135.69203.48527.61201.551024.48200.81
3 锚杆锚固机制
试件破坏形态如图12所示,观察图12可以发现,因试件几何相似比较大的原因,试件自由面破裂区域边界虽不明显,但仍可以看出锚固体临空面出现部分区域凹进,部分区域凸出的变形特征,这是因为无锚杆支护时试件破裂块体类似于松散体,而有锚杆支护时其托盘位置附近可形成锚固压缩区,远离托盘位置形成了非锚固区,其内部的块体缺乏有效支撑作用,拆除塑料薄膜后部分块体直接脱落。试件破裂方向主要沿近似垂直方向,试件出现压剪破坏而产生剪切裂纹,裂纹间相互交叉、贯穿,通过侧面裂隙分布图可以发现拉伸裂缝与剪切裂纹,明显的拉伸裂缝主要集中在临空面附近,而较大的剪切裂纹位于距离临空面较远的位置。拉伸裂纹的分布规律说明试件的破坏是由表及里的,多条纵向拉伸裂缝将试件分割成若干个类似于板状的结构,板状结构向临空面移动过程中,应力集中的存在会进一步诱导板状结构萌生剪切裂纹或拉伸裂纹,使板状结构失稳破裂成碎块,而结构的失稳反过来重新调整试件内部应力场,再次萌生新的裂隙,如此反复直至锚固系统平衡,在板状结构移动失稳过程中产生的变形即为非连续变形。

图12 试件破裂形态
Fig.12 Fracture morphology of specimens
根据断裂力学原理[18],裂纹的扩展最终大致与最大主应力方向平行,随载荷增加,裂纹长度将相应增长,当达到一定长度后,自由表面的存在导致裂纹非稳定扩展,从而使裂纹长度突然增长,形成平行于试件自由面的尺寸较大的劈裂裂纹。而贯通后的类似板梁的结构在纵向载荷的进一步作用下,会发生屈曲破坏。
板状结构的拉伸裂缝呈现出锚杆锚固位置处闭合,边缘张开的形式,体现了锚杆对板状结构的控制作用。根据以上分析,提出试件劈裂破坏的板状结构力学模型,简化为如图13所示的力学模型,即将似板状结构简化为板梁结构。在建立力学模型时如果精确考虑各方面的因素,得到的解可能会过于复杂,甚至有时还难以求解,为了求解的方便,一般都会进行一些必要的假设,如连续性、完全弹性、各向同性、材料均质等。本文建立板梁结构的目的在于在理论上描述试验现象,定性说明锚杆的作用,难以准确与试验数据相对应。
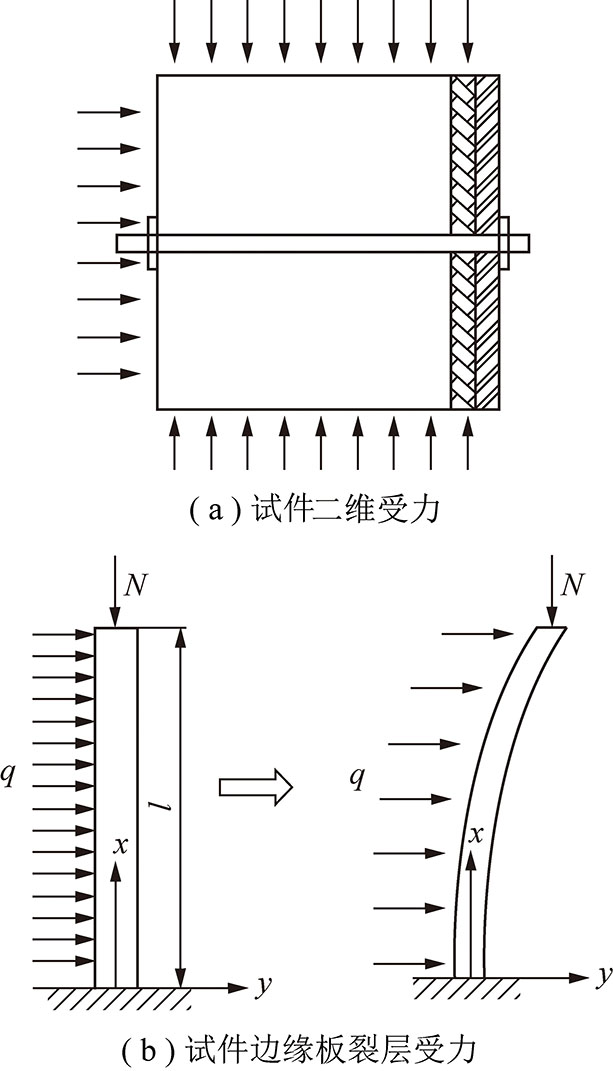
图13 支护1根锚杆时板梁力学模型
Fig.13 Mechanical model of plate-beam with one bolt
板梁受到的围岩压力视为均布载荷,试验机施加的轴向力为N,忽略板梁自身重力的影响。采用弹性平衡体系的能量原理分析该结构。由弹性理论可知,结构弯曲时,结构体系总势能W为弯曲变形能U和外载荷势能V之和:
![]()
(6)
其中,E为试件弹性模量;Iz为梁的惯性矩;N为试件垂直载荷;q为试件轴向力;l为梁的长度;w′,w″为挠度w的一阶,二阶导数。
总势能W为挠度w的泛函,其中w为变量,其余量都假定为已知的不变量。为使边界得到满足,设挠度w具有以下形式:
![]()
(7)
其中,δ为板梁结构端头位置的最大挠度。
根据最小势能原理,为使δ取得最小值,应使W满足:
![]()
(8)
求解得板梁结构端头的最大挠度为
![]()
(9)
其中,a=EIz/2。
挠度方程为
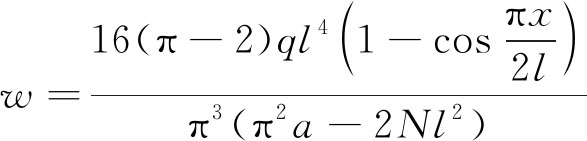
(10)
板梁的最大应力计算公式为
![]()
(11)
其中,d为梁沿y轴的厚度。
当梁受到的应力超过板梁极限强度后将出现破裂,最外层板梁发生破裂失稳后,试件向里逐层发生劈裂,不断产生新的板梁结构,内部板梁受到外部板梁的制约,挠度逐渐变小。锚杆的锚固位置处的板梁结构挠度最小,试件不易产生离层,随与锚固位置的距离加大,各板梁的弯曲破裂引起的试件非连续变形出现增大趋势,呈现出如图12所示外凸内凹的破坏形态。
从式(10)中可以看出板梁挠度除与试件自身力学性能、外载荷有关外,还与板梁的长度l有关。随锚杆密度增大,每根锚杆的作用区域减小,相当于两端固支的板梁结构,如图14所示。两端固支梁的挠度小于悬臂梁的挠度,且当锚杆支护密度增大,梁的长度l减小,挠度更小[19]。两端固支结构中间位置处的挠度最大,但小于单根锚杆作用下的梁端处的最大挠度。试件表面各处的非连续变形量近似等于锚杆延伸量与板梁挠度之和。因此,锚杆密度的增大改变了板梁结构,锚杆支护密度增大,试件非连续变形出现减小的趋势。
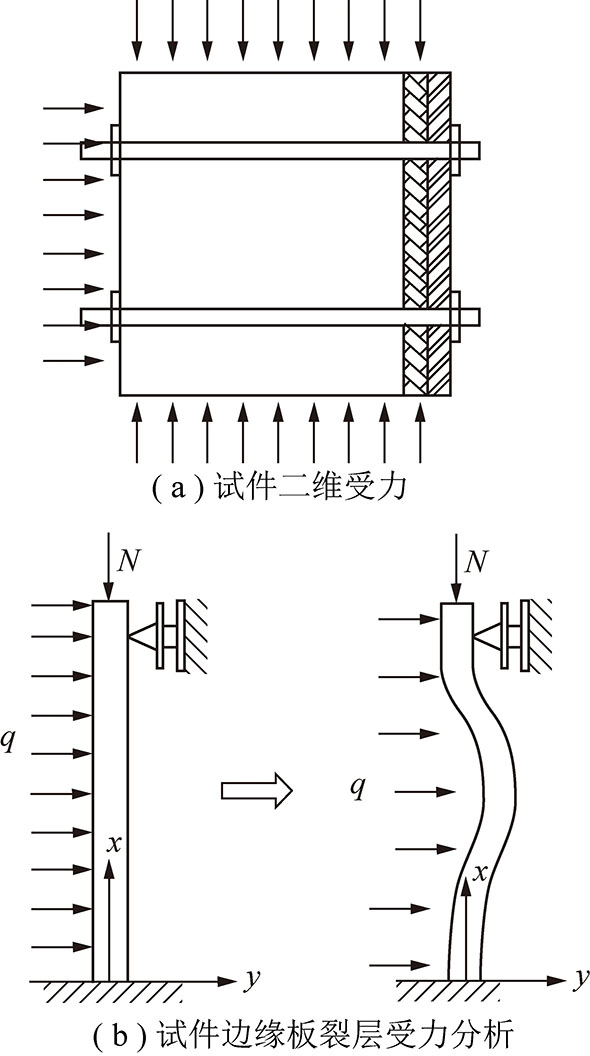
图14 支护2根锚杆时板梁力学模型
Fig.14 Mechanical Model of plate-beam with two bolts
对锚杆不施加预紧力或预紧力较小时,相当于被动支护,在锚杆锚固力起到较好的支护作用时,试件已经产生了较大的非连续变形,基本丧失了整体强度,后期残余强度完全由锚杆维持。对锚杆施加较大的预紧力能够实现主动支护,保证初期强度并防止因被动承载导致试件初始变形过大而破裂,难以形成稳定板梁结构;同时,施加较大的预紧力能使锚固区形成刚度较大的预应力承载结构,阻止劈裂板梁产生离层,同时改善围岩内部的应力状态,解释了为什么深部巷道围岩在锚杆支护作用下虽出现大变形现象但仍能保持一定的稳定性。
4 结 论
(1)锚杆支护密度及施加的预紧力与预裂试件的承载能力正相关,随着锚杆支护密度、预紧力增加,预裂试件的承载能力得到提高。无锚杆支护时,试件呈现脆性破坏,而安装锚杆后的试件应力应变曲线则出现较好的屈服平台,出现塑性流动现象,此时的试件在发生变形的同时仍能保持较高的承载能力。
(2)通过试验发现,在试件垂向位移量相近的情况下,沿锚杆轴向位移的大小则决定了试件体应变的大小,而随着锚杆支护密度及预紧力增大,试件的体积应变均出现降低。
(3)试件主要沿最大主应力方向(垂直方向)发生劈裂破坏,在锚杆作用下形成类似板梁结构,板梁挠度不仅与试件自身力学性能、外载荷有关,还与板梁长度、板梁形式有关。锚杆支护密度的增大改变了板梁结构形式,降低了板梁挠度。
(4)对于深部巷道,围岩给定变形是难以控制的,锚杆的主要作用是提高巷道破裂围岩的承载能力,提高围岩的整体性和连续性,减少破裂围岩的非连续变形。
[1] 王卫军,袁超,余伟健,等.深部大变形巷道围岩稳定性控制方法研究[J].煤炭学报,2016,41(12):2921-2931.
WANG Weijun,YUAN Chao,YU Weijian,et al.Stability control method of surrounding rock in deep roadway with large deformation[J].Journal of China Coal Society,2016,41(12):2921-2931.
[2] 马念杰,赵希栋,赵志强,等.深部采动巷道顶板稳定性分析与控制[J].煤炭学报,2015,40(10):2287-2295.
MA Nianjie,ZHAO Xidong,ZHAO Zhiqiang,et al.Stability analysis and control technology of mine roadway roof in deep mining[J].Journal of China Coal Society,2015,40(10):2287-2295.
[3] 康红普,范明建,高富强,等.超千米深井巷道围岩变形特征与支护技术[J].岩石力学与工程学报,2015,34(11):2227-2241.
KANG Hongpu,FAN Mingjian,GAO Fuqiang,et al.Deformation and support of rock roadway at depth more than 1 000 meters[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2227-2241.
[4] 赵志强.大变形回采巷道围岩变形破坏机理与控制方法研究[D].北京:中国矿业大学(北京),2014.
[5] 康红普.深部煤巷锚杆支护技术的研究与实践[J].煤矿开采,2008,13(1):1-5.
KANG Hongpu.Research and practice of bolting support technology in deep coal roadways[J].Coal Mining Technology,2008,13(1):1-5.
[6] 侯朝炯,勾攀峰.巷道锚杆支护围岩强度强化机理研究[J].岩石力学与工程学报,2000,19(3):342-345.
HOU Chaojiong,GOU Panfeng.Study of strengthening mechanism in surrounding rock strength for roadway bolt support[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(3):342-345.
[7] 孟波,靖洪文,杨旭旭,等.破裂围岩锚固体变形破坏特征试验研究[J].岩石力学与工程学报,2013,32(12):2497-2505.
MENG Bo,JING Hongwen,YANG Xuxu,et al.Exprimental study of deformation and failure characteristics of anchorage unit in fractured surrounding rocks[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(12):2497-2505.
[8] 董方庭.锚喷支护研究——围岩松动圈测定及锚固体强度实验(实验小结)[J].中国矿业学院学报,1980(2):29-40.
DONG Fangting.Investigation in shotcrete roof boltsupports:A study of zone of movement of surrounding rock and strength of anchored body[J].Journal of China University of Mining and Technology,1980(2):29-40.
[9] 李术才,王刚,王书刚,等.加锚断续节理岩体断裂损伤模型在硐室开挖与支护中的应用[J].岩石力学与工程学报,2006,25(8):1582-1590.
LI Shucai,WANG Gang,WANG Shugang,et al.Application of fracture-damage model to anchorage of discontinuous jointed rockmass of excavation and supporting[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(8):1582-1590.
[10] 王平,冯涛,朱永建,等.加锚预制裂隙类岩体锚固机制试验研究及其数值模拟[J].岩土力学,2016,37(3):793-801.
WANG Ping,FENG Tao,ZHU Yongjian,et al.Experimental study and numerical simulation of anchoring mechanism of anchored rocklike material with prefabricated fracture[J].Rock and Soil Mechanics,2016,37(3):793-801.
[11] 牛双建,靖洪文,杨旭旭,等.深部巷道破裂围岩强度衰减规律试验研究[J].岩石力学与工程学报,2012,31(8):1587-1596.
NIU Shuangjian,JING Hongwen,YANG Xuxu,et al.Experimental study of strength degradation law of surrounding rock in fractured zone of deep roadway[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(8):1587-1596.
[12] 袁璞,徐颖,薛俊华.锚固支护深部巷道爆破开挖模型试验研究[J].岩石力学与工程学报,2016,35(9):1830-1836.
YUAN Pu,XU Ying,XUE Junhua.Model test of anchorage deep tunnel in blasting excavation[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(9):1830-1836.
[13] 刘宁,张春生,褚卫江.深埋围岩破裂损伤深度分析与锚杆长度设计[J].岩石力学与工程学报,2015,34(11):2278-2284.
LIU Ning,ZHANG Chunsheng,CHU Weijiang.Depth of fracture and damage in deep-buried surrounding rock and bolt length design[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2278-2284.
[14] 董恩远,王卫军,马念杰,等.考虑围岩蠕变的锚固时空效应分析及控制技术[J].煤炭学报,2018,43(5):1238-1248.
DONG Enyuan,WANG Weijun,MA Nianjie,et al.Analysis of anchor space-time effect and research of control technology considering creep of surrounding rock[J].Journal of China Coal Society,2018,43(5):1238-1248.
[15] 朱文心,靖洪文,张力,等.锚杆作用下块状岩体力学特性试验研究[J].采矿与安全工程学报,2018,35(2):261-266.
ZHU Wenxin,JING Hongwen,ZHANG Li,et al.Experimental study on the mechanical properties of lumpy rock mass under bolt reinforcement[J].Journal of Mining & Safety Engineering,2018,35(2):261-266.
[16] JAEGER J C.Fundamentals of rock mechanics[M].Fundamentals of Rock Mechanics,1976.
[17] SZÜCS E. Similitude and modelling[M].New York:Elsevier Scientific Publishing Company,1980.
[18] 王自强,陈少华.高等断裂力学[M].北京:科学出版社,2009.
[19] 刘鸿文.材料力学(第5版)[M].北京:高等教育出版社,2011.
