岩爆是高地应力状态下地下硐室开挖过程中,硬脆性围岩因开挖卸荷导致洞壁切向应力超出围岩强度极限,引发岩体弹性能急剧猛烈释放而产生碎片剥落、岩块动力弹射抛掷现象,并伴有不同程度的爆炸、撕裂声,直接威胁现场作业人员和设备安全,影响工程进度[1-4]。
岩爆预测是岩爆灾害的有力防控手段[5]。岩爆预测方法主要分为两大类,即单因素预测方法以及多因素综合预测方法。前者利用已建立的岩爆判据实现岩爆烈度预测[2,6-13],判据不同,岩爆烈度判别结果稍有差别;后者利用非线性理论综合多种岩爆判据、岩石力学参数等实现岩爆预测,应用的非线性理论主要分为两类:数学方法和智能算法。前者主要结合模糊数学综合评判法[6]、可拓学理论[14]、逼近理想解排序法(TOPSIS)[15-16]、灰色系统理论[17]、云模型理论[18-19]、距离判别法[2]、理想点法[5,20]、未确知测度理论[21]等;后者主要应用BP神经网络[22]、支持向量机[23]、人工神经网络[24]、广义回归神经网络[25]等。与单因素预测方法相比,多因素综合预测方法考虑岩爆影响因素更为全面、判别结果较为准确,具有一定优势。此外,基于微震监测技术的岩爆预测也正逐步推广应用,该技术通过获取岩体内部产生微破裂的前兆信息,可实时反映出围岩应力状态及强度等物理力学参数的变化特征,实现岩爆预测[3,26-27]。
以上理论方法、技术从不同角度揭示了岩爆现象发生规律及指标特征,丰富了岩爆预测理论。由于岩爆影响因素较多,其孕育演化机制尚不明朗,需要充分利用指标信息、挖掘指标特征与岩爆烈度等级的内在联系,并结合多种预测理论方法、技术才有可能实现岩爆的准确预测,故仍有必要引入新的预测模型开展岩爆烈度分级预测方法研究。
概率神经网络(PNN)是由Specht于1988年提出的,具有结构简单、训练容易、收敛速度快,容错能力强等优点,并可用线性学习算法实现非线性学习算法的功能[28-29],主要应用于故障诊断等模式分类问题[30-31]。PNN网络的激活函数采用高斯函数时,指标变量需满足互不相关且同分布[32]。事实上,大多数岩爆预测指标间均存在一定的相关性,故应用PNN网络前需先消除岩爆预测指标间相关性。
消除指标间相关性的常用方法有限制指标数量、分离重迭元、修正指标权重、主成分分析法、因子分析法等[33]。考虑到本文选用预测指标较多,选用主成分分析法(PCA)对岩爆预测指标数据预处理,除可消除指标间的相关性外,还能实现指标数据降维,提高PNN网络训练和分类速度。由此笔者基于主成分分析-概率神经网络模型开展岩爆烈度分级预测方法研究。
1 方法原理
1.1 主成分分析法
主成分分析法的核心是将原指标通过线性组合,使之成为一组新的、互相独立的、并包含大部分原始信息的综合指标,以此达到降维的目的[34]。在保证原始数据足够信息量的前提下,对原多维指标变量数据进行降维,可压缩指标个数、简化数据,缩减岩爆烈度分级预测所消耗的时间。该法模型如下:
假定m个样本和n个评价指标中第i个样本的第j个指标取值为xij,构造原始评价指标数据矩阵X=(xij)m×n:
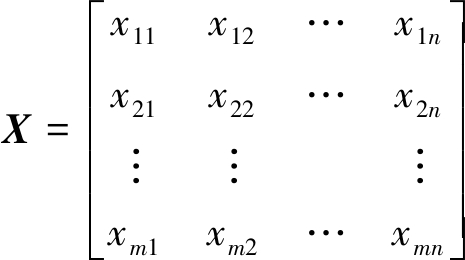
(1)
则原变量指标为x1,x2,…,xn,设降维后综合指标即主成分为y1,y2,…,yn,用X的n个指标向量作线性组合,即
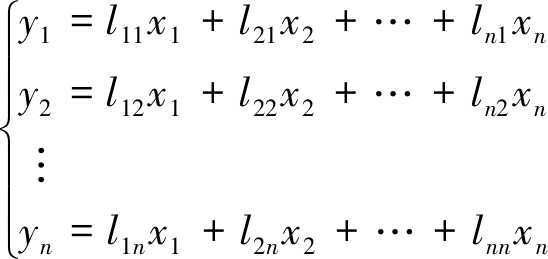
(2)
式(1),(2)满足:① 各等式系数平方和为1,如式(3)所示;② 任何两个主成分相互独立,互不相关;③ y1是x1,x2,…,xn的全部线性组合中方差最大者,y2是与y1不相关的x1,x2,…,xn的全部线性组合中方差最大者,yn是与y1,y2,…,yn-1均不相关的x1,x2,…,xn的全部线性组合中方差最大者[34]。
![]()
(3)
从相关矩阵出发求解主成分的步骤[35-36]。
步骤1:将原始数据标准化。
![]()
(4)
![]()
(5)
式中,![]() 和sj分别为第 j 个指标的均值和标准差。
和sj分别为第 j 个指标的均值和标准差。
步骤2:计算指标间的Pearson相关系数矩阵,即
R=(rkl)n×n (k,l=1,2,…,n)
(6)
其中,rkl为第k个指标和第l个指标间的相关系数,且rkl=rlk(即对称矩阵),计算公式为
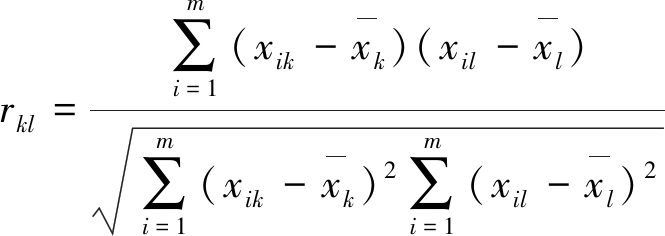
(7)
步骤3:计算相关矩阵R的特征值和特征向量。特征值记为λ1,λ2,…,λn,满足λi≥0(i=1,2,…,n),特征值对应的单位化特征向量记为p1,p2,…,pn。
步骤4:确定主成分个数。计算主成分的累计贡献率,一般取特征值大于1、累计贡献率达85%~95%所对应的前k个主成分。
![]()
(8)
式中,vs为第s个主成分的方差贡献率。
![]()
(9)
式中,vsumk为前k个主成分的累计贡献率。
步骤5:计算提取主成分的对应得分。主成分系数矩阵为:U=(p1,p2,…,pn),若从原指标中提取了前k个主成分,则有
![]()
(10)
式中,X*为原数据的标准化矩阵,![]() 为标准化后的指标变量。
为标准化后的指标变量。
1.2 概率神经网络
概率神经网络以径向基神经网络为基础,采用统计学方法推导的激活函数替换S型激活函数,在某些易满足的条件下由PNN实现的决策边界渐近趋向贝叶斯最优决策面[28],是径向基网络与贝叶斯决策理论、概率密度函数的非参数估计的有机融合。PNN网络由输入层、模式层、累加层和输出层组成,其网络拓扑结构如图1[37]所示。输入层接收训练样本数据,神经元个数与输入向量长度相等,输入向量经加权处理后传递给模式层见式(11):
Zi=xwi
(11)
式中,Zi为模式层第i个神经元的输入;x为输入向量;wi为权值向量。
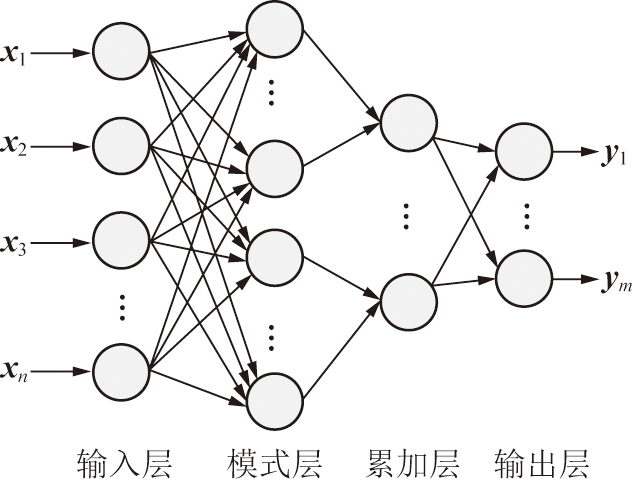
图1 概率神经网络拓扑结构
Fig.1 Probabilistic neural network topology
模式层用来计算输入向量与各模式的匹配关系,并返回一个标量值。该层神经元个数与输入的训练样本个数相同。向量x输入到模式层,则模式层中第i类模式的第j个神经元输出关系为
φij=1/[(2π)0.5σd]e[-(x-xij)(x-xij)T/σ2]
(12)
式中,d为度量空间的维数;σ为平滑因子;xij为第i类样本的第j个中心;φij为模式层中第i类模式的第j个神经元输出值。
累加层的主要作用是线性求和、加权平均。将模式层中同一模式的神经元的输出做加权平均,该层神经元数目与样本模式总数相同,且与模式层神经元建立连接关系的前提条件是两者属于同一模式分类。
![]()
(13)
式中,vi为第i类类别的输出,(i=1,2,…,M),M为训练样本模式总数;L表示第i类神经元的个数。
输出层由竞争神经元构成,神经元个数与训练样本模式总数相同,每个神经元分别对应一种模式。用于为累加层的输出做临界值判别,将输出层内具有最大后验概率密度的神经元输出为1,其余输出为0。
2 岩爆烈度预测模型
2.1 PNN适用性分析
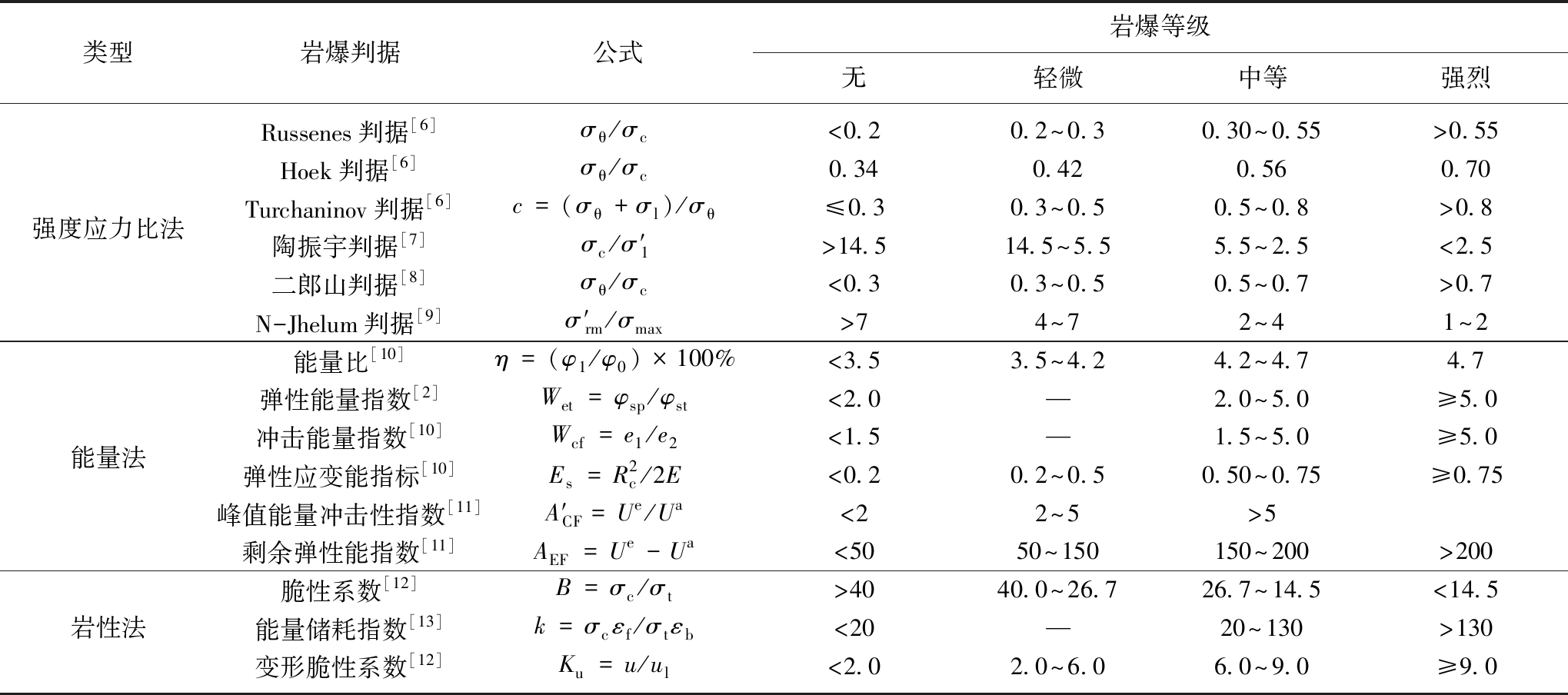
将岩爆烈度分级预测视为模式分类问题的依据(即PNN适用性)如下:① 岩爆烈度有分级。关于岩爆烈度分级国内外目前虽尚无统一标准,目前常用的岩爆判据见表1。由表1可知,岩爆烈度常被分为4级,即岩爆烈度预测结果共有4类;② 岩爆预测问题有相应的指标量化数据,且一组样本有惟一确定的岩爆烈度;③ 岩爆预测问题的基本思路主要是通过对岩爆指标变量数据的非线性处理,挖掘预测指标与岩爆烈度的内在联系,使模型判定结果能够与实际岩爆等级一致,达到预测的目的。该过程与PNN模式分类问题相似,即先通过岩爆典型样本训练学习预测指标与岩爆等级间的对应关系,进而将训练后的PNN网络判定测试样本岩爆等级。
表1 岩爆判据及烈度分级
Table 1 Rockburst criterion and intensity classification
类型岩爆判据公式岩爆等级无轻微中等强烈Russenes判据[6]σθ/σc<0.20.2~0.30.30~0.55>0.55Hoek判据[6]σθ/σc0.340.420.560.70强度应力比法Turchaninov判据[6]c=(σθ+σl)/σθ≤0.30.3~0.50.5~0.8>0.8陶振宇判据[7]σc/σ′1>14.514.5~5.55.5~2.5<2.5二郎山判据[8]σθ/σc<0.30.3~0.50.5~0.7>0.7N-Jhelum判据[9]σ′rm/σmax>74~72~41~2能量比[10]η=(φ1/φ0)×100%<3.53.5~4.24.2~4.74.7弹性能量指数[2]Wet=φsp/φst<2.0—2.0~5.0≥5.0能量法冲击能量指数[10]Wcf=e1/e2<1.5—1.5~5.0≥5.0弹性应变能指标[10]Es=R2c/2E<0.20.2~0.50.50~0.75≥0.75峰值能量冲击性指数[11]A′CF=Ue/Ua<22~5>5剩余弹性能指数[11]AEF=Ue-Ua<5050~150150~200>200脆性系数[12]B=σc/σt>4040.0~26.726.7~14.5<14.5岩性法能量储耗指数[13]k=σcεf/σtεb<20—20~130>130变形脆性系数[12]Ku=u/ul<2.02.0~6.06.0~9.0≥9.0
注:σθ为硐室最大切向应力,MPa;σc为岩石单轴抗压强度,MPa;σl为硐室轴向应力,MPa;σ′1为最大主应力,MPa;σ′rm为岩体强度,MPa;σmax为垂直于隧道轴向的最大水平主应力,MPa;η为能量比;φ1为破坏后岩石碎片弹射的动能,kJ/m3;φ0为岩石受载后储存的最大弹性应变能,kJ/m3;Wet为弹性能量指数;φsp为岩石试件在单轴压缩过程中,达到σc以前(0.8σc~0.9σc)所存储的弹性应变能,kJ/m3;φst为一个加载循环中产生微破裂和岩石塑性变形所耗损能量,kJ/m3;Wcf为冲击能量指数;e1为峰值前贮存的变形能;e2为破坏过程损耗的变形能;Es为弹性应变能指标;E为岩石的弹性模量,GPa;A′CF为峰值能量冲击性指数;AEF为剩余弹性能指数;Ue,Ua分别为峰前弹性能密度和峰后破坏能密度,kJ/m3;B为脆性系数;k为能量储耗指数;Ku为变形脆性系数;σt为岩石单轴抗拉强度,MPa;εf,εb为峰值前和峰值后的总应变量;u,ul为岩石峰值荷载前的总变形和永久变形。
2.2 岩爆预测指标选取
岩爆的发生与岩体特征、地应力、地质构造和开挖扰动等因素密切相关[9],具有显著的随机性、突发性和复杂性等特点[38-39],给岩爆预测带来了较大挑战。岩爆预测的数据信息源于选取的指标,目前岩爆预测指标体系多数基于3~6种岩爆判据或岩石力学参数。总的来说,预测指标的选取应满足:① 在室内或现场易于获取,具有较好的可操作性;② 具有较好的代表性;③ 能够从不同角度反映岩爆特征信息。利用上述已有研究成果,根据岩爆的影响因素、特点及成因,选取围岩最大切应力σθ、单轴抗压强度σc、单轴抗拉强度σt、应力系数σθ/σc、脆性系数σc/σt和弹性能量指数Wet六种指标组成岩爆预测指标体系。前3种为围岩应力参数,后3种为岩爆判据(岩爆烈度分级标准见表1)。
2.3 PCA-PNN岩爆烈度预测模型
主要过程为:① 根据选定指标搜集岩爆案例数据;② 为消除指标间量纲、数量级差异,将原始数据标准化,再作相关性分析;③ 采用主成分分析法(PCA)对数据预处理,消除指标间相关性并降维,得到主成分数据;④ 创建PNN网络,设置不同的平滑因子;⑤ 将训练样本数据输入PNN进行训练,获取各类样本的特征信息;⑥ 训练完成后,分别输入训练样本和测试样本对网络性能测试,计算其分类正确率。
由表1可知,岩爆烈度分级有无、轻微、中等、强烈4类,笔者将该分级分别设定为1,2,3,4级,则PNN输出向量为1×4行向量,类别编码采用第i类在行向量第i个元素位置输出为1、其余为0,如输出向量为(0,1,0,0)表示该样本属于2级,即轻微岩爆。
3 预测模型实现过程
3.1 PCA预处理
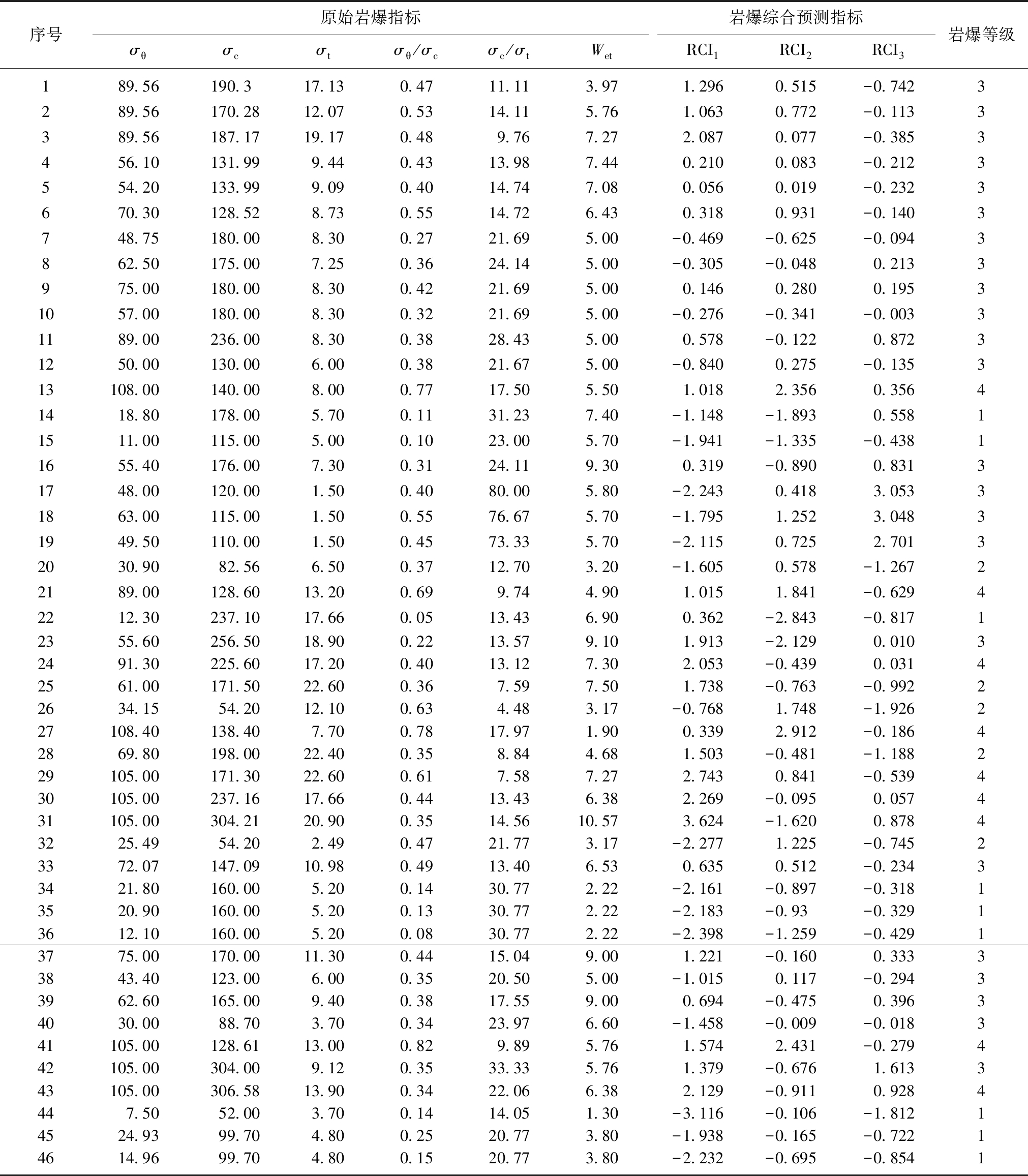
依据所选指标,笔者搜集国内外46组典型工程岩爆案例数据[12,40-42](表2),前36组为训练样本,后10组作为测试样本。
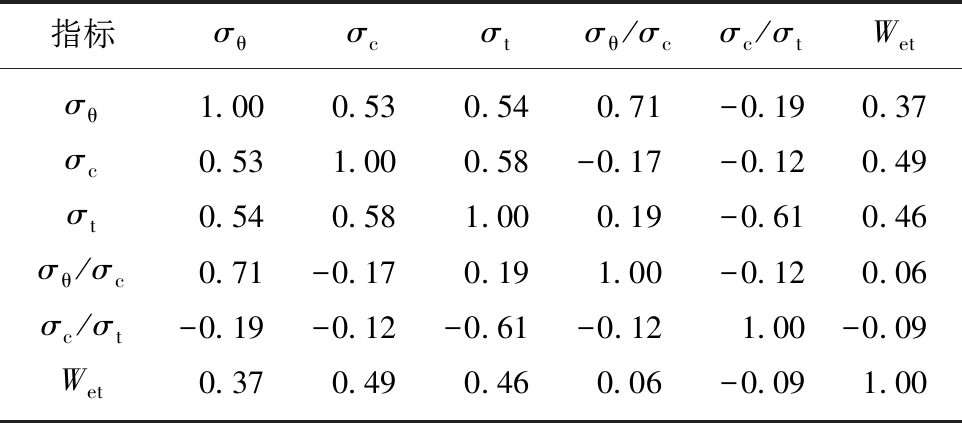
各指标间相关系数见表3,σc与σt,σt与σc/σt,σθ与σc,σt,σθ/σc的相关系数均超过0.5,预测指标间有较为明显的相关性,岩爆烈度分级预测结果必定会受其影响,故有必要采用主成分分析法对原始数据作相关性消除处理。
表2 原始岩爆案例数据与主成分数据
Table 2 Data of original rockburst cases and principal components
序号原始岩爆指标σθσcσtσθ/σcσc/σtWet岩爆综合预测指标RCI1RCI2RCI3岩爆等级189.56190.317.130.4711.113.971.2960.515-0.7423289.56170.2812.070.5314.115.761.0630.772-0.1133389.56187.1719.170.489.767.272.0870.077-0.3853456.10131.999.440.4313.987.440.2100.083-0.2123554.20133.999.090.4014.747.080.0560.019-0.2323670.30128.528.730.5514.726.430.3180.931-0.1403748.75180.008.300.2721.695.00-0.469-0.625-0.0943862.50175.007.250.3624.145.00-0.305-0.0480.2133975.00180.008.300.4221.695.000.1460.2800.19531057.00180.008.300.3221.695.00-0.276-0.341-0.00331189.00236.008.300.3828.435.000.578-0.1220.87231250.00130.006.000.3821.675.00-0.8400.275-0.135313108.00140.008.000.7717.505.501.0182.3560.35641418.80178.005.700.1131.237.40-1.148-1.8930.55811511.00115.005.000.1023.005.70-1.941-1.335-0.43811655.40176.007.300.3124.119.300.319-0.8900.83131748.00120.001.500.4080.005.80-2.2430.4183.05331863.00115.001.500.5576.675.70-1.7951.2523.04831949.50110.001.500.4573.335.70-2.1150.7252.70132030.9082.566.500.3712.703.20-1.6050.578-1.26722189.00128.6013.200.699.744.901.0151.841-0.62942212.30237.1017.660.0513.436.900.362-2.843-0.81712355.60256.5018.900.2213.579.101.913-2.1290.01032491.30225.6017.200.4013.127.302.053-0.4390.03142561.00171.5022.600.367.597.501.738-0.763-0.99222634.1554.2012.100.634.483.17-0.7681.748-1.926227108.40138.407.700.7817.971.900.3392.912-0.18642869.80198.0022.400.358.844.681.503-0.481-1.188229105.00171.3022.600.617.587.272.7430.841-0.539430105.00237.1617.660.4413.436.382.269-0.0950.057431105.00304.2120.900.3514.5610.573.624-1.6200.87843225.4954.202.490.4721.773.17-2.2771.225-0.74523372.07147.0910.980.4913.406.530.6350.512-0.23433421.80160.005.200.1430.772.22-2.161-0.897-0.31813520.90160.005.200.1330.772.22-2.183-0.93-0.32913612.10160.005.200.0830.772.22-2.398-1.259-0.42913775.00170.0011.300.4415.049.001.221-0.1600.33333843.40123.006.000.3520.505.00-1.0150.117-0.29433962.60165.009.400.3817.559.000.694-0.4750.39634030.0088.703.700.3423.976.60-1.458-0.009-0.018341105.00128.6113.000.829.895.761.5742.431-0.279442105.00304.009.120.3533.335.761.379-0.6761.613343105.00306.5813.900.3422.066.382.129-0.9110.9284447.5052.003.700.1414.051.30-3.116-0.106-1.81214524.9399.704.800.2520.773.80-1.938-0.165-0.72214614.9699.704.800.1520.773.80-2.232-0.695-0.8541
注:37~46组为测试样本,表7同。
表3 各指标间相关系数
Table 3 Correlation coefficients between different indexes
指标σθσcσtσθ/σcσc/σtWetσθ1.000.530.540.71-0.190.37σc0.531.000.58-0.17-0.120.49σt0.540.581.000.19-0.610.46σθ/σc0.71-0.170.191.00-0.120.06σc/σt-0.19-0.12-0.61-0.121.00-0.09Wet0.370.490.460.06-0.091.00
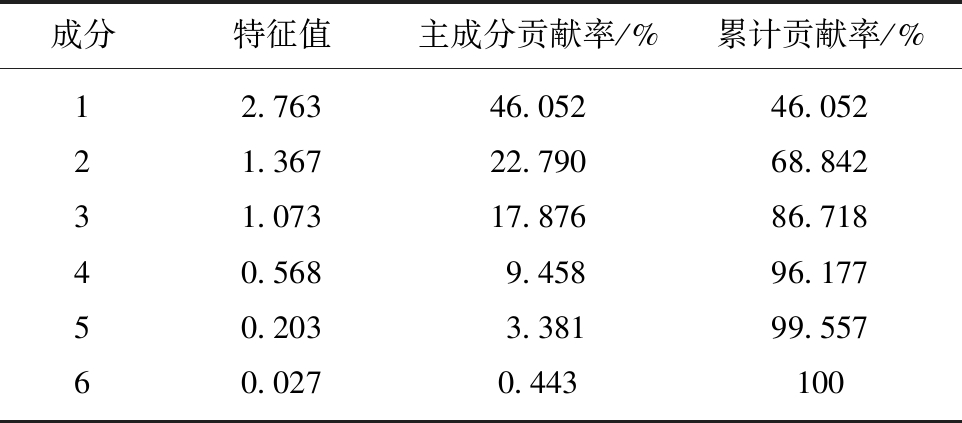
采用标准化的46组岩爆案例数据作主成分分析,其计算步骤如前文所述。各主成分方差贡献率及累计贡献率见表4,前3个主成分的累计贡献率达86.718%,表明前3个主成分共包含86.718%的原始信息,且对应的特征值均大于1,满足前述条件,因此选取这3个主成分。表5为主成分系数矩阵,由此得出主成分y1,y2,y3与6个指标变量之间的关系为
![]()
(14)
![]()
(15)
![]()
(16)
表4 PCA处理后的结果
Table 4 Results by PCA
成分特征值主成分贡献率/%累计贡献率/%12.76346.05246.05221.36722.79068.84231.07317.87686.71840.5689.45896.17750.2033.38199.55760.0270.443100
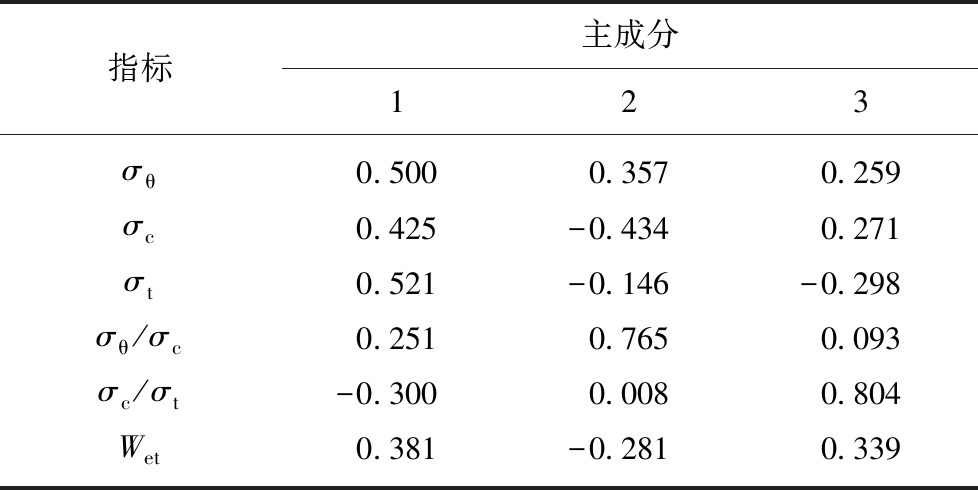
表5 主成分系数矩阵
Table 5 Coefficient matrix of principal components
指标主成分123σθ0.5000.3570.259σc0.425-0.4340.271σt0.521-0.146-0.298σθ/σc0.2510.7650.093σc/σt-0.3000.0080.804Wet0.381-0.2810.339
用式(1),(2)将指标数据标准化后代入式(14),(15),(16),可得主成分数据(表2)。3个主成分包含了原指标中的绝大部分信息,故可将3个主成分视为岩爆综合预测指标RCI1,RCI2,RCI3。
3.2 PNN网络参数确定
各组岩爆综合预测指标RCI1,RCI2,RCI3构成PNN网络输入向量。训练样本数据有36组,岩爆烈度有4种分类模式,因此PNN输入层、模式层、累加层、输出层的神经元个数分别为3,36,4,4,其拓扑网络结构为3×36×4×4。先输入36组训练样本对PNN进行训练,再分别输入训练样本、10组测试样本对网络性能进行测试。
平滑因子的选取对网络性能起着关键作用。平滑因子取值过小易造成网络过度拟合[43];平滑因子取值过大则不能完全区分细节,PNN网络接近于线形分类器[44]。本文考虑平滑因子Spread值取值区间为[0.02,1.00],满足区间内均匀分布,共50个Spread值。经测试,岩爆训练样本、测试样本的预测正确率随Spread值的变化曲线如图2所示。
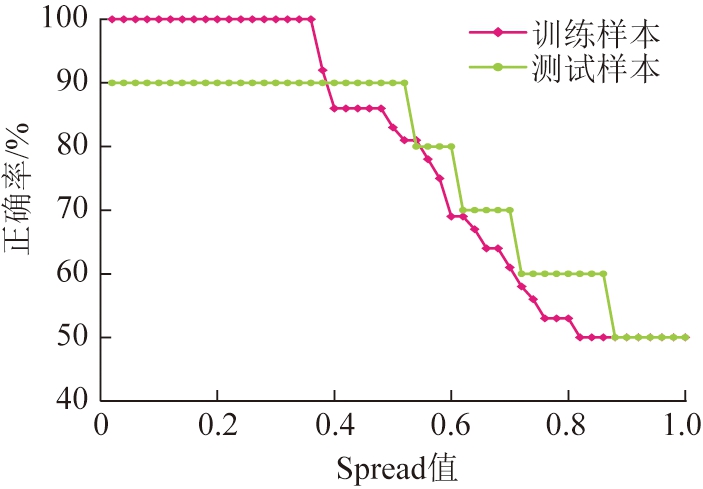
图2 模型预测正确率随Spread值的变化
Fig.2 Accuracy rate of the model prediction changes with Spread values
由图2可知,在0.02~1.00,训练样本、测试样本预测正确率总体上随平滑因子的减小而趋增高;在某些小范围内,训练样本正确率、测试样本正确率不随平滑因子变化,说明PNN网络对这些区间内的spread值变化不敏感。训练样本、测试样本正确率最大值及首次达到最大时的spread值见表6。
表6 模型最优结果及对应参数
Table 6 Optimal results and corresponding parameters
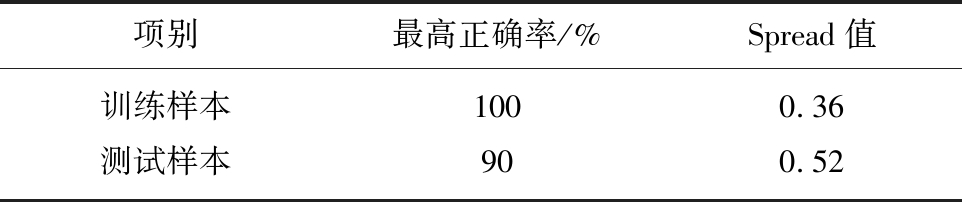
项别最高正确率/%Spread值训练样本1000.36测试样本900.52
3.3 PCA-PNN模型预测结果
取Spread值为0.36,46组岩爆案例判定结果如图3,4所示。由图3,4可知,训练样本测试误判率为0,测试样本中第8组岩爆案例误判,预测结果比实际发生的岩爆等级略大一级,误判率为10%。
为进一步说明模型的可行性,将预测结果与随机森林(RF)模型、支持向量机(SVM)模型及人工神经网络(ANN)模型的两组预测结果[40]对比,具体见表7。由表7可知,4种模型的预测结果相差不大,与实际岩爆烈度基本吻合。RF模型、SVM模型及ANN模型的训练样本误判率、测试样本误判率见表8。由表8可知,PCA-PNN模型比SVM模型及ANN模型预测效果稍好,误判率与RF模型训练样本平均误判率、测试样本平均误判率一致。此外PNN收敛速度快,通常在数秒内即可完成,且分类效果较为理想,表明PCA-PNN岩爆烈度分级预测模型是合理可行的。
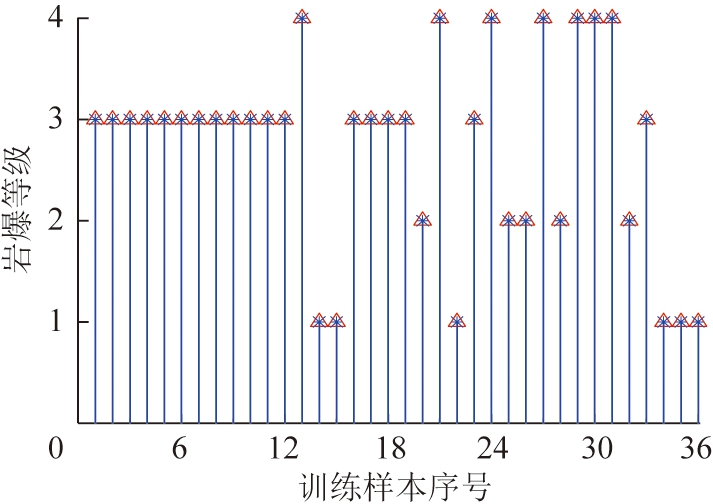
图3 训练样本预测结果
Fig.3 Training sample prediction results
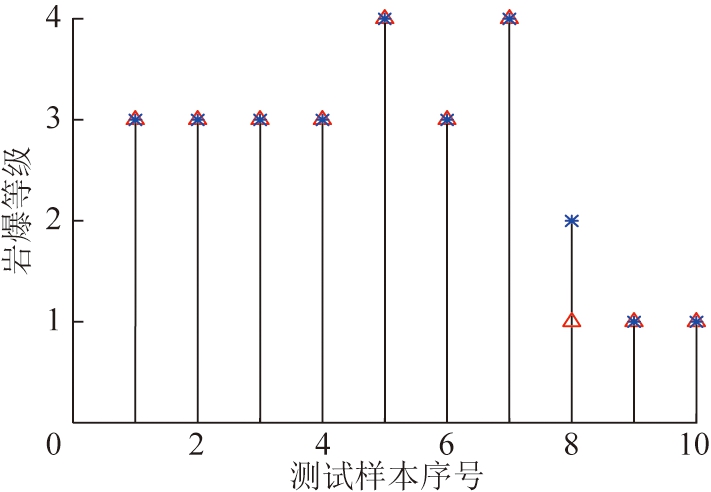
图4 测试样本预测结果
Fig.4 Test sample prediction results
表7 与其它模型预测结果对比
Table 7 Contrast with other model predictions
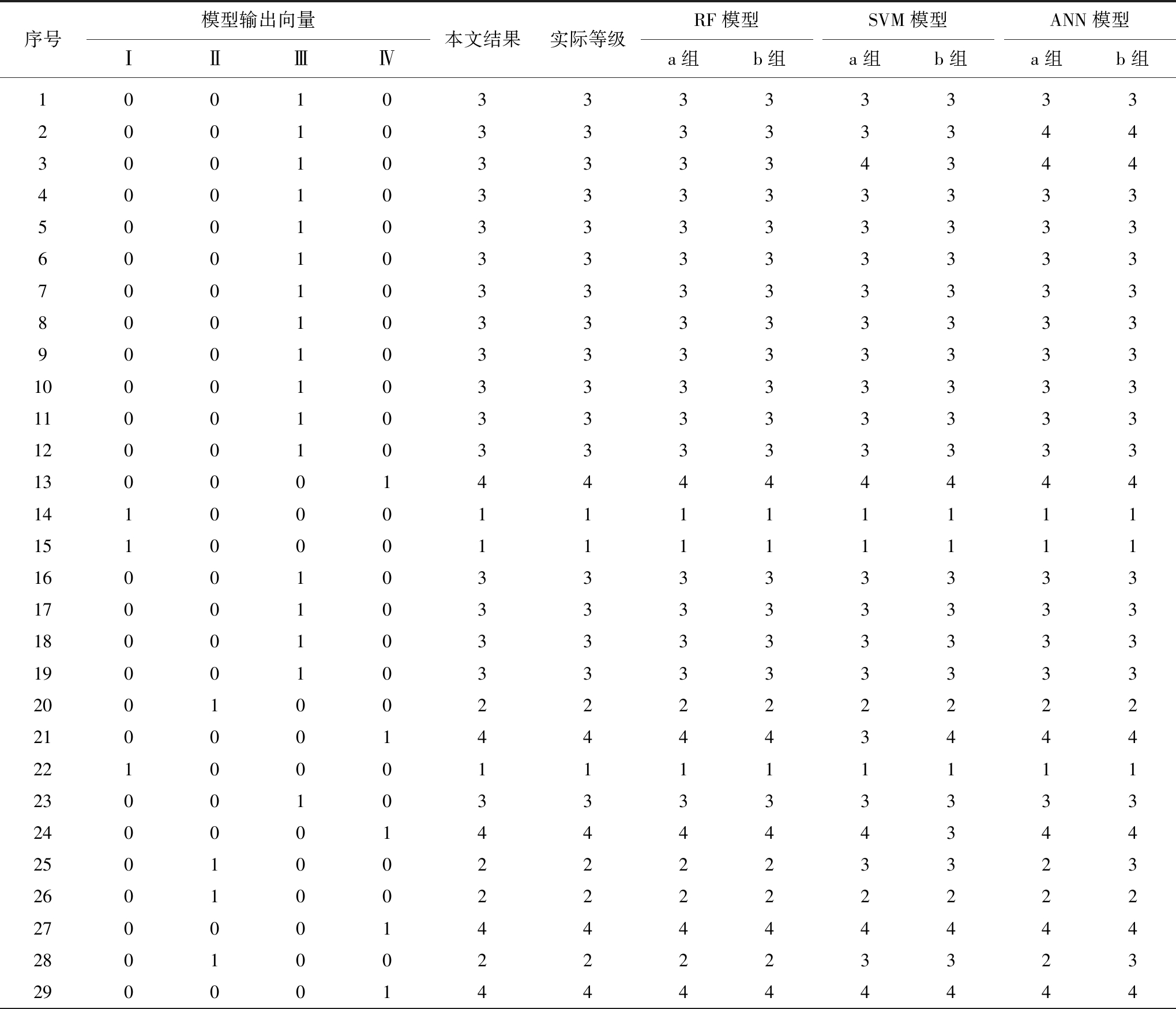
序号模型输出向量ⅠⅡⅢⅣ本文结果实际等级RF模型a组b组SVM模型a组b组ANN模型a组b组1001033333333200103333334430010333343444001033333333500103333333360010333333337001033333333800103333333390010333333331000103333333311001033333333120010333333331300014444444414100011111111151000111111111600103333333317001033333333180010333333331900103333333320010022222222210001444434442210001111111123001033333333240001444443442501002222332326010022222222270001444444442801002222332329000144444444
续 表
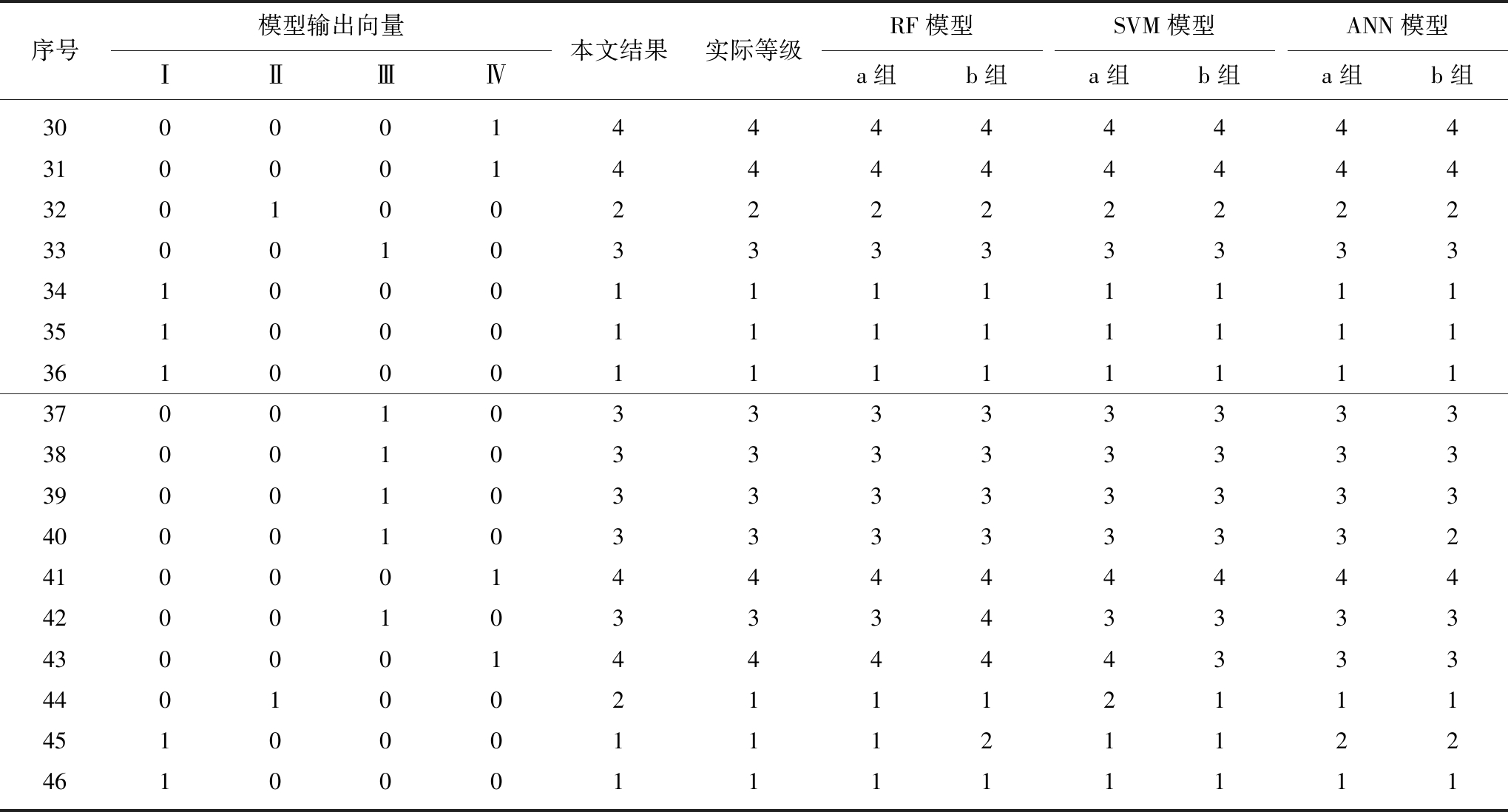
序号模型输出向量ⅠⅡⅢⅣ本文结果实际等级RF模型a组b组SVM模型a组b组ANN模型a组b组3000014444444431000144444444320100222222223300103333333334100011111111351000111111113610001111111137001033333333380010333333333900103333333340001033333332410001444444444200103334333343000144444333440100211121114510001112112246100011111111
表8 3种模型误判率汇总[40]
Table 8 Summary of misjudgment rates of three other models[40]

误判率RF模型a组b组SVM模型a组b组ANN模型a组b组训练样本误判率/%0011.18.35.611.1测试样本误判率/%02010102030训练样本平均误判率/%09.708.35测试样本平均误判率/%101025
4 结 论
(1)选取围岩最大切应力σθ、单轴抗压强度σc、单轴抗拉强度σt、应力系数σθ/σc、脆性系数σc/σt和弹性能量指数Wet共6个指标构成岩爆预测指标体系。考虑到指标间的相关性及PNN网络对指标变量间相互独立的要求,采用主成分分析法对原始数据预处理,消除指标相关性并降维,得出3个线性无关的主成分即岩爆综合预测指标RCI1,RCI2,RCI3。
(2)平滑因子σ(Spread值)对概率神经网络性能影响较大。在满足均匀分布的前提下,选取[0.02,1.00]内的50个Spread值,经测试训练样本、测试样本正确率最大值分别为100%,90%,两者首次达到最大时对应的Spread值分别为0.36,0.52。
(3)为使训练样本、测试样本正确率同时最优,取Spread值为0.36。并将判别结果与RF模型、SVM模型及ANN模型的两组预测结果比较,发现4种模型之间预测结果总体相差不大,但PCA-PNN模型比SVM模型、ANN模型的预测结果稍好,误判率与RF模型的训练样本平均误判率、测试样本平均误判率一致。此外PNN收敛速度快,通常在数秒内即可完成,效果较为理想。以上表明PCA-PNN岩爆烈度分级预测模型是合理可行的。
[1] 裴启涛,李海波,刘亚群,等.基于组合赋权的岩爆倾向性预测灰评估模型及应用[J].岩土力学,2014,35(S1):49-56.
PEI Qitao,LI Haibo,LIU Yaqun,et al.A grey evaluation model for predicting rockburst proneness based on combination weight and its application[J].Rock and Soil Mechanics,2014,35(S1):49-56.
[2] 宫凤强,李夕兵.岩爆发生和烈度分级预测的距离判别方法及应用[J].岩石力学与工程学报,2007,26(5):1012-1018.
GONG Fengqiang,LI Xibing.Distance discrimination method for rockburst occurrence and intensity classification prediction and its application[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):1012-1018.
[3] 冯夏庭,陈炳瑞,张传庆,等.岩爆孕育过程的机制、预警与动态调控[M].北京:科学出版社,2013:1-18.
[4] 谭以安.岩爆特征及岩体结构效应[J].中国科学(B辑),1991(9):985-991.
TAN Yian.Rockburst characteristics and rock mass structure effects[J].Science in China(Series B),1991(9):985-991.
[5] 徐琛,刘晓丽,王恩志,等.基于组合权重-理想点法的应变型岩爆五因素预测分级[J].岩土工程学报,2017,39(12):2245-2252.
XU Chen,LIU Xiaoli,WANG Enzhi,et al.Prediction and classification of strain mode rockburst based on five-factor criterion and combined weight-ideal point method[J].Chinese Journal of Geotechnical Engineering,2017,39(12):2245-2252.
[6] 王元汉,李卧东,李启光,等.岩爆预测的模糊数学综合评判方法[J].岩石力学与工程学报,1998,17(5):15-23.
WANG Yuanhan,LI Wodong,LI Qiguang,et al.Rockburst prediction based on fuzzy mathematics comprehensive evaluation method[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(5):15-23.
[7] 张镜剑,傅冰骏.岩爆及其判据和防治[J].岩石力学与工程学报,2008,27(10):2034-2042.
ZHANG Jingjian,FU Bingjun.Rockburst and its criteria and control[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2034-2042.
[8] 徐林生,王兰生.二郎山公路隧道岩爆发生规律与岩爆预测研究[J].岩土工程学报,1999,21(5):569-572.
XU Linsheng,WANG Lansheng.Study on the laws of rockburst and its forecasting in the tunnel of Erlang Mountain road[J].Chinese Journal of Geotechnical Engineering,1999,21(5):569-572.
[9] MA C S,CHEN W Z,TAN X J,et al.Novel rockburst criterion based on the TBM tunnel construction of the Neelum-Jhelum (NJ)hydroelectric project in Pakistan[J].Tunnelling and Underground Space Technology,2018,81:391-402.
[10] 张传庆,卢景景,陈珺,等.岩爆倾向性指标及其相互关系探讨[J].岩土力学,2017,38(5):1397-1404.
ZHANG Chuanqing,LU Jingjing,CHEN Jun,et al.Discussion on rock burst proneness indexes and their relation[J].Rock and Soil Mechanics,2017,38(5):1397-1404.
[11] 宫凤强,闫景一,李夕兵.基于线性储能规律和剩余弹性能指数的岩爆倾向性判据[J].岩石力学与工程学报,2018,37(9):1993-2014.
GONG Fengqiang,YAN Jingyi,LI Xibing.A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(9):1993-2014.
[12] ZHOU J,LI X,SHI X.Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines[J].Safety Science,2012,50(4):629-644.
[13] 唐礼忠,王文星.一种新的岩爆倾向性指标[J].岩石力学与工程学报,2002,21(6):874-878.
TANG Lizhong,WANG Wenxing.New rock burst proneness index[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(6):874-878.
[14] 张乐文,张德永,邱道宏.基于粗糙集的可拓评判在岩爆预测中的应用[J].煤炭学报,2010,35(9):1461-1465.
ZHANG Lewen,ZHANG Deyong,QIU Daohong.Application of extension evaluation method in rockburst prediction based on rough set theory[J].Journal of China Coal Society,2010,35(9):1461-1465.
[15] 龚剑,胡乃联,崔翔,等.基于AHP-TOPSIS评判模型的岩爆倾向性预测[J].岩石力学与工程学报,2014,33(7):1442-1448.
GONG Jian,HU Nailian,CUI Xiang,et al.Rockburst tendency prediction based on AHP-TOPSIS evaluation model[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1442-1448.
[16] 周科平,雷涛,胡建华.深部金属矿山RS-TOPSIS岩爆预测模型及其应用[J].岩石力学与工程学报,2013,32(S2):3705-3711.
ZHOU Keping,LEI Tao,HU Jianhua.RS-TOPSIS model of Rockburst prediction in deep metal mines and its application[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(S2):3705-3711.
[17] 裴启涛,李海波,刘亚群,等.基于改进的灰评估模型在岩爆中的预测研究[J].岩石力学与工程学报,2013,32(10):2088-2093.
PEI Qitao,LI Haibo,LIU Yaqun,et al.Rockburst prediction based on a modified grey evaluation model[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(10):2088-2093.
[18] 李绍红,王少阳,朱建东,等.基于权重融合和云模型的岩爆倾向性预测研究[J].岩土工程学报,2018,40(6):1075-1083.
LI Shaohong,WANG Shaoyang,ZHU Jiandong,et al.Prediction of rock burst tendency based on weighted fusion and improved cloud model[J].Chinese Journal of Geotechnical Engineering,2018,40(6):1075-1083.
[19] 过江,张为星,赵岩.岩爆预测的多维云模型综合评判方法[J].岩石力学与工程学报,2018,37(5):1199-1206.
GUO Jiang,ZHANG Weixing,ZHAO Yan.A multidimen-sional cloud model for rockburst prediction[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(5):1199-1206.
[20] XU C,LIU X,WANG E,et al.Rockburst prediction and classification based on the ideal-point method of information theory[J].Tunnelling and Underground Space Technology,2018,81:382-390.
[21] 史秀志,周健,董蕾,等.未确知测度模型在岩爆烈度分级预测中的应用[J].岩石力学与工程学报,2010,29(S1):2720-2726.
SHI Xiuzhi,ZHOU Jian,DONG Lei,et al.Application of unascertained measurement model to prediction of classification of rockburst Intensity[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S1):2720-2726.
[22] 李永松,尹健民,艾凯.BP神经网络在岩爆预测中的应用[J].长江科学院院报,2008(5):183-185,190.
LI Yongsong,YIN Jianmin,AI Kai.Application of BP neural network in prediction of rockburst[J].Journal of Yangtze River Scientific Research Institute,2008(5):183-185,190.
[23] 李宁,王李管,贾明涛.基于粗糙集理论和支持向量机的岩爆预测[J].中南大学学报(自然科学版),2017,48(5):1268-1275.
LI Ning,WANG Liguan,JIA Mingtao.Rockburst prediction based on rough set theory and support vector machine[J].Journal of Central South University (Science and Technology),2017,48(5):1268-1275.
[24] 张光存,高谦,杜聚强,等.基于人工神经网络及非线性回归的岩爆判据[J].中南大学学报(自然科学版),2013,44(7):2977-2981.
ZHANG Guangcun,GAO Qian,DU Juqiang,et al.Rockburst criterion based on artificial neural networks and nonlinear regression[J].Journal of Central South University (Science and Technology),2013,44(7):2977-2981.
[25] 贾义鹏,吕庆,尚岳全.基于粒子群算法和广义回归神经网络的岩爆预测[J].岩石力学与工程学报,2013,32(2):343-348.
JIA Yipeng,LÜ Qing,SHANG Yuequan.Rockburst prediction using particle swarm optimization and generalized regression neural network[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(2):343-348.
[26] 马天辉,唐春安,唐烈先,等.基于微震监测技术的岩爆预测机制研究[J].岩石力学与工程学报,2016,35(3):470-483.
MA Tianhui,TANG Chun’an,TANG Liexian,et al.Mechanism of Rockburst forcasting based on micro-seismic monitoring technology[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(3):470-483.
[27] 张文东,马天辉,唐春安,等.锦屏二级水电站引水隧洞岩爆特征及微震监测规律研究[J].岩石力学与工程学报,2014,33(2):339-348.
ZHANG Wendong,MA Tianhui,TANG Chun’an,et al.Research on characteristics of rockburst and rules of microseismic monitoring at diversion tunnels of Jinping II Hydropower Station[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(2):339-348.
[28] 陈明.MATLAB神经网络原理与实例精解[M].北京:清华大学出版社,2013:205-207.
[29] 史忠植.神经网络[M].北京:高等教育出版社,2009:203-210.
[30] 叶志锋,孙健国.基于概率神经网络的发动机故障诊断[J].航空学报,2002,23(2):155-157.
YE Zhifeng,SUN Jianguo.Probabilistic neural network based engine fault diagnosis[J].Acta Aeronautica et Astronautica Sinica,2002,23(2):155-157.
[31] 梁晴晴,韩华,崔晓钰,等.基于主元分析-概率神经网络的制冷系统故障诊断[J].化工学报,2016,67(3):1022-1031.
LIANG Qingqing,HAN Hua,CUI Xiaoyu,et al.Fault diagnosis for refrigeration system based on PCA-PNN[J].CIESC Journal,2016,67(3):1022-1031.
[32] 易军,李太福,田应甫,等.基于对称Alpha稳定分布概率神经网络的铝电解槽况诊断[J].化工学报,2012,63(10):3196-3201.
YI Jun,LI Taifu,TIAN Yingfu,et al.Diagnosis of status of aluminum reduction cells based on Symmetric Alpha-stable probabilistic Neural Network[J].CIESC Journal,2012,63(10):3196-3201.
[33] 徐祥发,肖人彬.评价指标相关性的消除方法研究[J].系统工程理论与实践,2002,11:1-5.
XU Xiangfa,XIAO Renbin.An approach of eliminating correlation of assessment-index[J].System Engineering Theory and Practice,2002,11:1-5.
[34] 任雪松,于秀林.多元统计分析(第2版)[M].北京:中国统计出版社,2011:184-198.
[35] 汪冬华,马艳梅.多元统计分析与SPSS应用(第2版)[M].上海:华东理工大学出版社,2018:192-206.
[36] 张文彤,董伟.SPSS统计分析高级教程(第3版)[M].北京:高等教育出版社,2018:239-244.
[37] Specht D F.Probabilistic neural networks[J].Neural Networks,1990,3(1):109-118.
[38] 吴顺川,周喻,高斌.卸载岩爆试验及PFC3D数值模拟研究[J].岩石力学与工程学报,2010,29(S2):4082-4088.
WU Shunchuan,ZHOU Yu,GAO Bin.Study of unloading tests of rockburst and PFC3D numerical simulation[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S2):4082-4088.
[39] 高永涛,周兴国,吴顺川,等.深埋隧道白云岩试样岩爆模拟实验研究[J].北京科技大学学报,2010,32(7):819-826.
GAO Yongtao,ZHOU Xingguo,WU Shunchuan,et al.Simulation experimental investigation on rockburst of dolomite specimens at great depth tunnel[J].Journal of University of Science and Technology Beijing,2010,32(7):819-826.
[40] DONG L J,XIBING L I,PENG K.Prediction of rockburst classification using Random Forest[J].Transactions of Nonferrous Metals Society of China,2013,23(2):472-477.
[41] AFRAEI S,SHAHRIAR K,MADANI S H.Developing intelligent classification models for rock burst prediction after recognizing significant predictor variables,Section 1:Literature review and data preprocessing procedure[J].Tunnelling and Underground Space Technology,2019,83:324-353.
[42] 杨涛,李国维.基于先验知识的岩爆预测研究[J].岩石力学与工程学报,2000,19(4):429-431.
YANG Tao,LI Guowei.Study on rockburst prediction method based on the prior knowledge[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(4):429-431.
[43] 张国亮,杨春玲,王暕来.基于优化概率神经网络和红外多光谱融合的大气层外空间弹道目标识别[J].电子与信息学报,2014,36(4):896-903.
ZHANG Guoliang,YANG Chunling,WANG Jianlai.Discrimination of exo-atmospheric targets based on optimization of probabilistic neural network and ir multispectral fusion[J].Journal of Electronics & Information Technology,2014,36(4):896-903.
[44] 田立.基于鱼群优化概率神经网络算法的研究[D].沈阳:辽宁大学,2014:39-41.
TIAN Li.Researches of probabilistic neural networks optimized by ash swarm algorithm[D].Shenyang:Liaoning University,2014:39-41.
