在地质调查和岩体工程建设中经常会遇到大量天然岩石中富含近似弧形裂隙现象。在外来荷载的作用下，这些已经存在的裂隙尖端附近很容易萌生新的裂纹，新生裂纹的扩展可能会导致岩石工程失稳[1-5]。近年来国内外众多学者针对直线型缺陷岩石力学特性开展了大量的研究工作，取得了一系列研究成果[6-12]，然而对于含非直线型裂隙岩石力学特征研究涉及较少，相关研究鲜有报道，因此开展研究非直线型缺陷岩石的力学问题对岩石工程的稳定控制具有重要意义。
国内外岩石力学研究学者通过在类岩石和真实岩石材料中预制不同参数的直线型裂隙，研究裂隙参数对岩石裂隙力学特征的影响。NEMAT等[13]分别对单轴和双轴压缩条件下直线型裂隙相互影响开展试验研究，研究表明预制裂隙倾角是控制尖端主生裂隙扩展方向和试样破坏模式的有效参数之一，并利用断裂力学分析了在整体远场压缩作用下预制直裂纹的平面扩展机制，对裂纹生长过程的各种参数进行了量化。WONG等[14]在类岩石材料中预制平行裂隙，通过单轴压缩研究裂纹贯通模式及峰值强度，提出了含平行裂隙缺陷试样的破坏规则。WONG和CHAU等[15]分析了单轴压缩下断续双裂隙大理岩的强度和裂纹扩展特征，得到裂隙倾角对试样破坏模式的影响规律。杨圣奇[16]对断续三裂隙砂岩试样进行了单轴压缩试验，通过照相测量技术研究了不同裂隙倾角对砂岩强度和裂纹扩展的影响规律，并给出了三裂隙砂岩试样宏观变形特性与裂纹扩展过程之间的关系。YANG等[17-18]分析了预制断续单裂隙脆性砂岩的力学特征，探讨了裂隙长度和裂隙倾角对脆性砂岩强度和变形参数、AE分布规律以及裂纹扩展机制的影响。熊飞等[19]通过对含尖端相交裂隙砂岩试样进行单轴压缩试验，研究了2条相交裂隙分布方向角β和夹角α对砂岩强度、变形及破裂演化特征的影响，并利用声发射记录了试样加载过程中的声发射特征，在宏观裂纹的起裂、扩展和贯通过程中都会产生明显的AE事件。
数字照相和声发射技术作为监测裂纹扩展规律重要技术手段，已经广泛应用于岩石力学研究领域。NGUYEN等[20]采用数字照相量测技术，研究了平面应变条件下断续裂隙Neapolitan凝灰岩的裂纹扩展特征，加强了对软岩中裂纹扩展机制的理解;YIN等[21]在花岗岩中预制表面裂隙，并借助数字散斑相关技术研究了不同岩桥倾角的平行裂隙试样中裂纹贯通模式以及应变场变化规律。在数值模拟和理论分析方面也取得了大量的研究成果，XIE等[22]利用声发射仪对层状岩盐单轴压缩全过程进行数据采集，结合分形理论，提出了一种分析岩石损伤过程中AE数分形性质的方法。
以上文献针对含直线型裂隙缺陷砂岩试样的力学特性进行了大量的研究工作，众多研究表明含预制裂隙缺陷岩石强度会明显劣化，裂隙的形态、大小、位置和方向对岩石的破坏演化过程起着至关重要作用。然而在自然界中，岩石中的裂隙形状并不规则，除了前人研究的裂隙形态外还含有大量的非直线型裂隙。目前已经有学者开展相关方面的研究工作，MA等[23]通过3D打印技术，在材料中设置正弦裂隙，通过单轴压缩试验研究倾斜角度和有效曲率对预制裂纹的影响，研究认为当有效曲率小于2/7.5时，正弦裂纹的开裂以尖端开裂的形式为主;当有效曲率大于2/7.5时，裂纹起裂以非尖端裂纹形式出现。但针对非直线型岩石力学相关特征研究还不够全面，基于此笔者对含预制弧形裂隙砂岩进行室内单轴压缩，研究弧形裂隙的γ(弧形拱顶高度a与弦长b/2比值)对砂岩基本力学参数、声发射特征、破裂演化过程及破坏模式的影响规律，并探讨弧形裂隙尖端裂纹扩展力学机制。
1 试 验
1.1 试样制备
本试验所需黄砂岩岩样采自山东临沂市，该类岩石自然状态下呈浅黄色，质地较为致密均匀，表面无孔洞裂隙缺陷，主要成分为石英和长石，平均密度为2.16 g/cm3。
参照前人试样制作方法，本文对大块岩样进行切割打磨，制作成尺寸为(160±2) mm×(80±2) mm×(30±2) mm长方体板状试样。利用高压水射流切割机试样中心切割出弦长b为40±1 mm，拱高a分别为2，5，8，12，16和20 mm，其误差值均在-1～+1 mm内，试样加工如图1所示。为减小试样离散性对试验数据分析影响，每种试样制作2块，完整试样2块，共计14块试样。
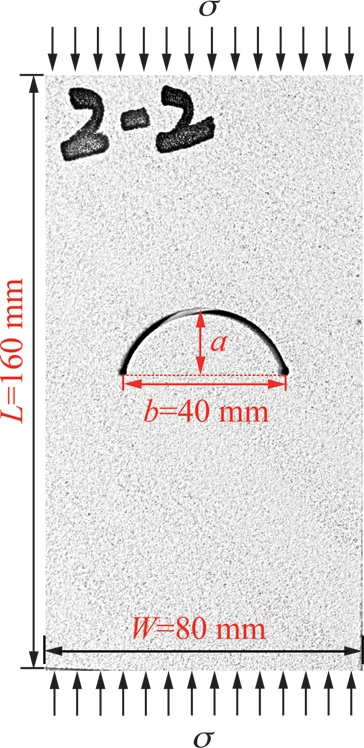
图1 试样及弧形预制裂隙几何形态示意
Fig.1 Diagram of the arc prefabricated fissure in the sandstone sample
1.2 试验设备
试验系统包括加载系统和数据采集系统如图2所示，加载系统为中国矿业大学YNS-2000型电液伺服试验机，该试验机提供的荷载为0～2 000 kN，加载方式为位移控制加载，加载速度为0.02 mm/min，在进行单轴压缩试验前，为减小试样端部摩擦效应，在试样与加载板之间均匀涂抹一层凡士林。试验数据采集系统主要包括应力应变数据采集、DS2声发射数据采集系统和数字图像采集系统，数字图像采集利用高速摄像机对试样的加载破裂演化过程进行实时采集。
图2 试验加载及数据采集系统
Fig.2 YNS2000 electro-hydraulic servo test machine and the data acquisition system
2 试验结果分析
2.1 轴向应力-应变曲线
单轴压缩作用下2个完整黄砂岩试样的应力-应变曲线如图3(a)所示，2个完整试样的峰值强度、峰值应变、平均弹性模量和割线模量的平均值分别为47.94 MPa，10.20×10-3，57.4 GPa和40.9 GPa，离散系数分别为1.42×10-2，3.9×10-2，2.6×10-2和5.4×10-2。由此可以看出本文所选用的黄砂岩均质性较好，力学参数离散性较小，适合对预制弧形裂隙砂岩力学特性进行定量研究分析。
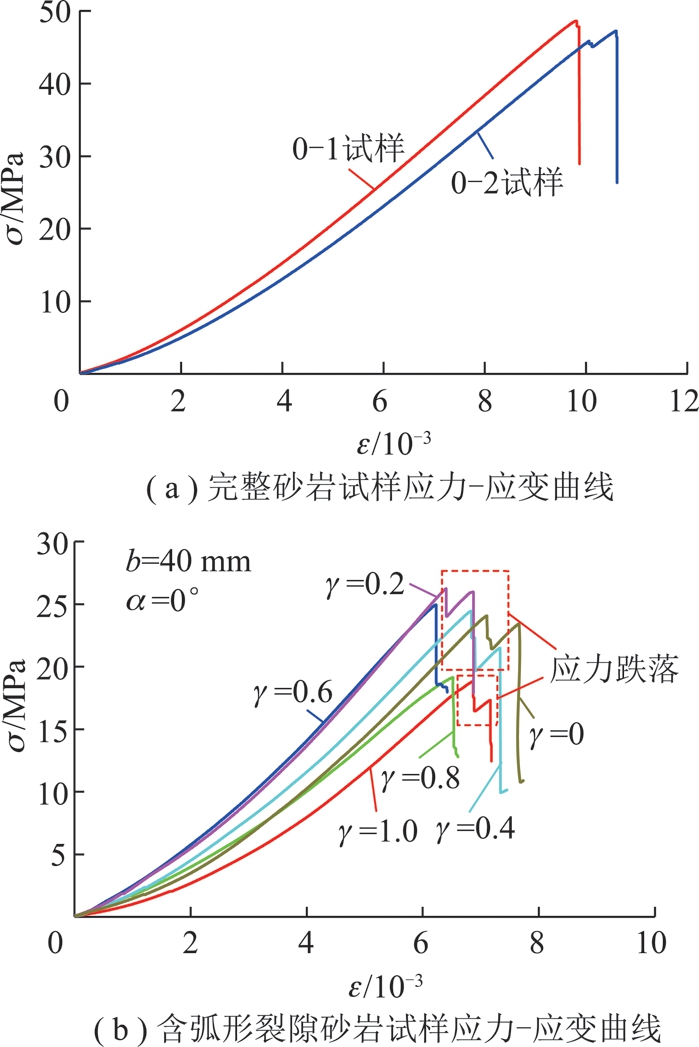
图3 完整黄砂岩和含弧形裂隙砂岩试样应力-应变曲线
Fig.3 Stress-strain curves of the intact and arc fissures sandstone samples
完整试样应力-应变曲线分孔隙裂隙压密段、弹性变形至微弹性裂隙稳定发展阶段、非稳定破裂发展阶段、破裂后阶段。从图3(a)可以看出轴向压力在0～10 MPa内2个试样均处于孔隙裂隙压密阶段表现出明显的非线性特征，该段σ-ε曲线呈现比较明显的上凹型，说明完整的黄砂岩内部的微裂纹和孔洞发育比较丰富，此阶段主要是微裂纹与微孔洞闭合引起的;随着位移的增加当轴向应力超过10 MPa后，试样σ-ε曲线进入线弹性阶段，此阶段轴向应力与轴向应变之间呈现近似直线性关系。0-2号试样轴向应力达到45.84 MPa(对应轴向应变为10.06×10-3)出现首次应力跌落，应力跌落至45.45 MPa(对应轴向应变为10.07×10-3)，应力跌落幅度为0.39 MPa。0-1号试样在峰值强度前未出现明显的应力跌落现象，当达到峰值强度时，试样内部承载结构遭到整体破坏，试样失去承载能力，应力迅速跌落至0。曲线在到达峰值应力之前基本未发生应力跌落，仍保持较好的线性特征，没有明显的屈服阶段，说明黄砂岩试样的脆性特征较为显著。
不同γ试样应力-应变曲线如图3(b)所示，由图可看出:与完整黄砂岩试样应力-应变曲线相比，γ=0，0.2，0.4和1.0四种弧形裂隙缺陷试样峰值强度后均有不同程度的应力跌落现象，表明试样峰值强度后仍具有一定的承载能力，弧形裂隙缺陷砂岩试样随着γ的增大，应力跌落幅度逐渐降低，峰后试样的承载能力逐渐降低。γ=0时，试样首次应力跌落点处轴向应力和轴向应变分别为24.95 MPa和6.93×10-3，分别为其峰值强度和峰值应变的94.43%和100.93%，随后应力出现反复的升降现象;γ=0.6和0.8试样达到峰值强度后并未出现应力跌落现象，而是试样整体失去承载能力，轴向应力跌落至0;γ=1时，试样首次应力跌落点处轴向应力和轴向应变分别为16.55 MPa和6.94×10-3，分别为其峰值强度和峰值应变的87.92%和101.02%，随后出现应力上升后迅速下降至0的过程，与γ=0试样相比首次应力跌幅较大。由此可见，γ对弧形裂隙黄砂岩试样的峰后特征具有重要的影响作用，γ越大，试样的峰后承载能力就越弱。
2.2 力学参数特征
由图4(a)～(c)可以看出与完整黄砂岩试样相比，单轴压缩作用下弧形裂隙缺陷砂岩力学参数出现了明显的劣化现象。图4(a)表明随着γ的增大，弧形裂隙砂岩峰值强度出现总体劣化趋势，试样峰值强度仅为完整试样平均峰值强度的38.67%～54.34%。在γ=0.4～0.6内峰值强度劣化程度处于稳定状态，但当γ在0.6～0.8内峰值强度劣化程度加剧，峰值强度由24.33 MPa降至20.13 MPa，降幅达17.27%。当γ=1时，试样平均峰值强度最小，其值为18.99 MPa，表明γ在0.6～1.0内对试样峰值强度的劣化最为明显。由图4(b)可以看出试样峰值应变为完整试样平均峰值应变的65.21%～70.12%。与试样峰值强度劣化趋势相似，峰值应变总体表现为随γ值增大而呈减小趋势。当γ=0时，试样峰值应变最大，其值为6.97×10-3;当γ=0.6时，试样峰值应变为6.64×10-3。可见在γ=0～0.6内，试样峰值应变劣化程度较小基本趋于稳定。当γ=0.8和1.0时，试样峰值应变分别降至为6.49×10-3和6.37×10-3，与γ=0.6的试样峰值应变相比分别减少了0.35×10-3和0.47×10-3。由图4(c)和(d)可以看出，随着γ值的增加，弧形裂隙砂岩试样的平均模量和割线模量均出现先增大后减小趋势。弧形裂隙砂岩试样的平均弹性模量和割线模量分别为完整试样平均值的65.70%～91.00%和49.42%～70.30%，γ值从0增大到1，试样的平均弹性模量由53.6 GPa降低到38.7 GPa，降幅为27.80%，割线模量由30.3 GPa减小到21.3 GPa，降幅为29.70%。
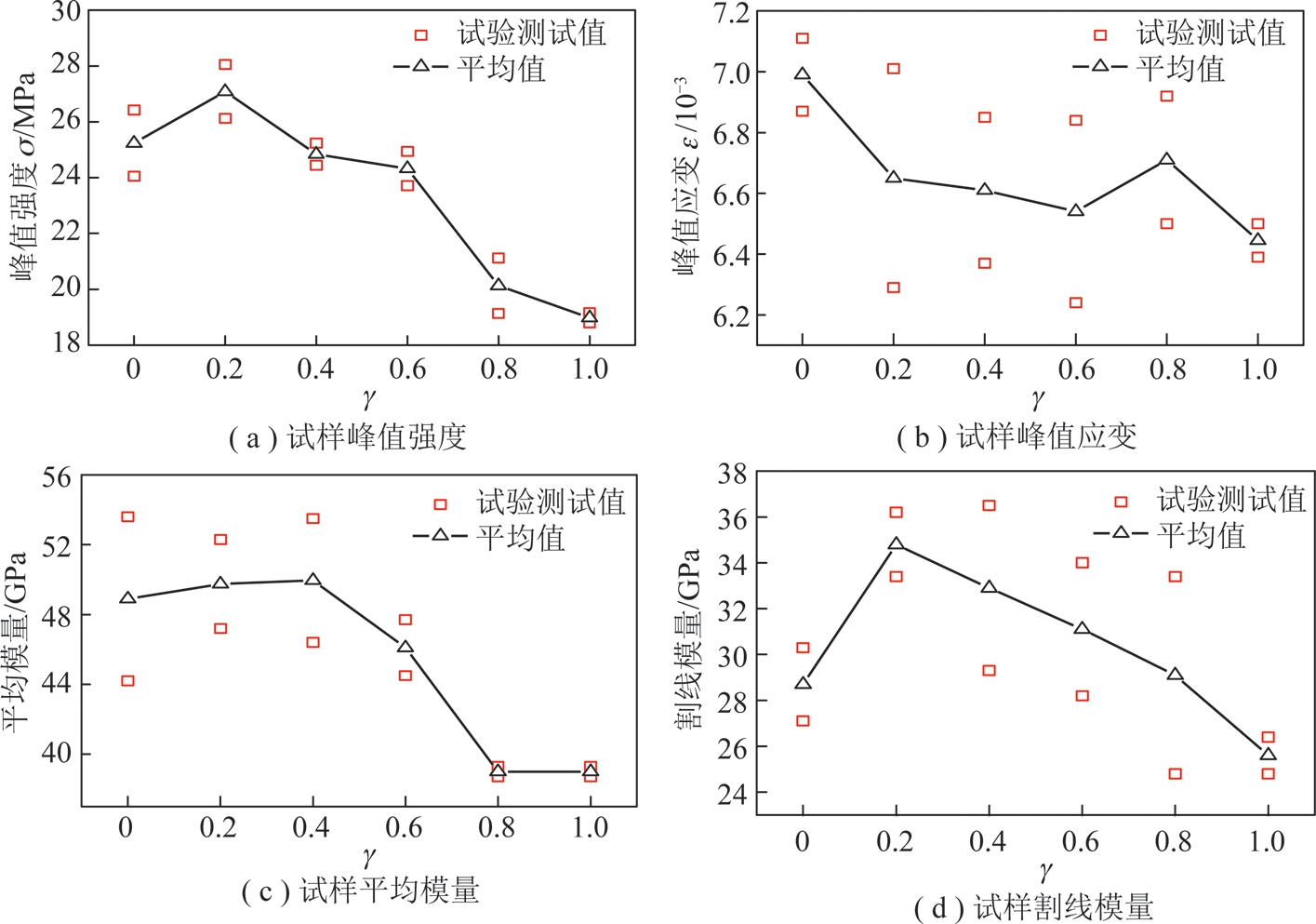
图4 不同γ值试样基本物理力学参数
Fig.4 Stress-strain curves and mechanical parameters
2.3 试样破坏演化及破坏形态
2.3.1 声发射与破裂演化特征
岩石材料在外力作用下内部裂纹萌生和扩展引起的能量释放现象称为声发射，声发射信号特征能实时反映岩石内部裂纹的动态演化过程[24]。根据岩石试件在受压过程中声发射信号特征(能量计数和振铃计数)，可将黄砂岩试样应力-时间曲线划分为5个阶段:① 压密阶段(OA)，在这个阶段中岩石内部裂纹闭合导致较小振幅的声发射产生，但由于岩石各向异性、非均匀性，声发射事件比较杂乱;② 弹性阶段(AB)，产生少量的声发射;③ 稳定破裂阶段(BC)，声发射多为突发型的，比弹性阶段声发射信号强度、事件总数有所提高;④ 非稳定破裂阶段(CD)，此段声发射活动急剧增多;⑤ 峰后阶段(DE)，此阶段能量计数率达到峰值，特别是在峰后拐点处声发射信号基本上达到峰值[25]。
图5为不同γ值试样在单轴压缩下声发射特征，由图5(a)～(f)可以看出在初始压密阶段，γ=1试样声发射现象较为明显，累计声发射次数明显增大，其余试样声发射现象并不明显，累计声发射次数呈缓慢增加趋势。这是由于弧形裂隙γ越大，裂隙尖端处受到的集中应力也就越大，在压密过程中除了部分矿物颗粒摩擦碰撞、微裂隙的咬合产生少量声发射外，主要是尖端处开始产生拉伸破裂产生密集声发射事件。
在弹性变形阶段试样的声发射事件并不明显，没有较大的声发射事件发生，累计声发射曲线几乎处于一个缓慢上升状态，表明该阶段6种试样内部并未发生大的破裂过程，没有明显的能量释放，而是聚集了较多的弹性能量。
在峰值强度前试样进入非稳定破坏阶段，试样内部尖端处裂纹扩展迅速，声发射活动变得非常活跃，在首次应力跌落即试样初次破裂时，试样释放大量能量，声发射次数显著增加，累计声发射曲线陡然上升。在试样完全破坏的瞬间声发射数达到最大值，表明弧形预制裂隙黄砂岩试样依然具有较大的脆性，试样整体破坏的瞬间释放大量能量。由图5还可以看出，随着γ值的增大累计声发射数整体减小趋势，γ为0.8时，累计声发射事件数最小，γ为0.2时，累计声发射事件数最大。这也表明γ值越大，即弧形弧度越大越容易发生拉伸破坏。
屈服强度是试样抵抗其微量塑形变形的应力，屈服点C的确定是研究固体力学机械性的一项重要评价指标。由图5(a)～(f)可知砂岩压缩过程中阶段划分的A，B，C三个分界点不易从试样强度曲线上判断，但根据声发射信息可较好的进行识别，识别过程需根据振铃计数、能量计数的特征判断，并同时参考应力-时间的曲线进行综合判定，笔者根据MARTIN[26]等提出的计算方法，定义单轴加载条件下C点为试样屈服点，C点对应的强度为试件屈服强度。
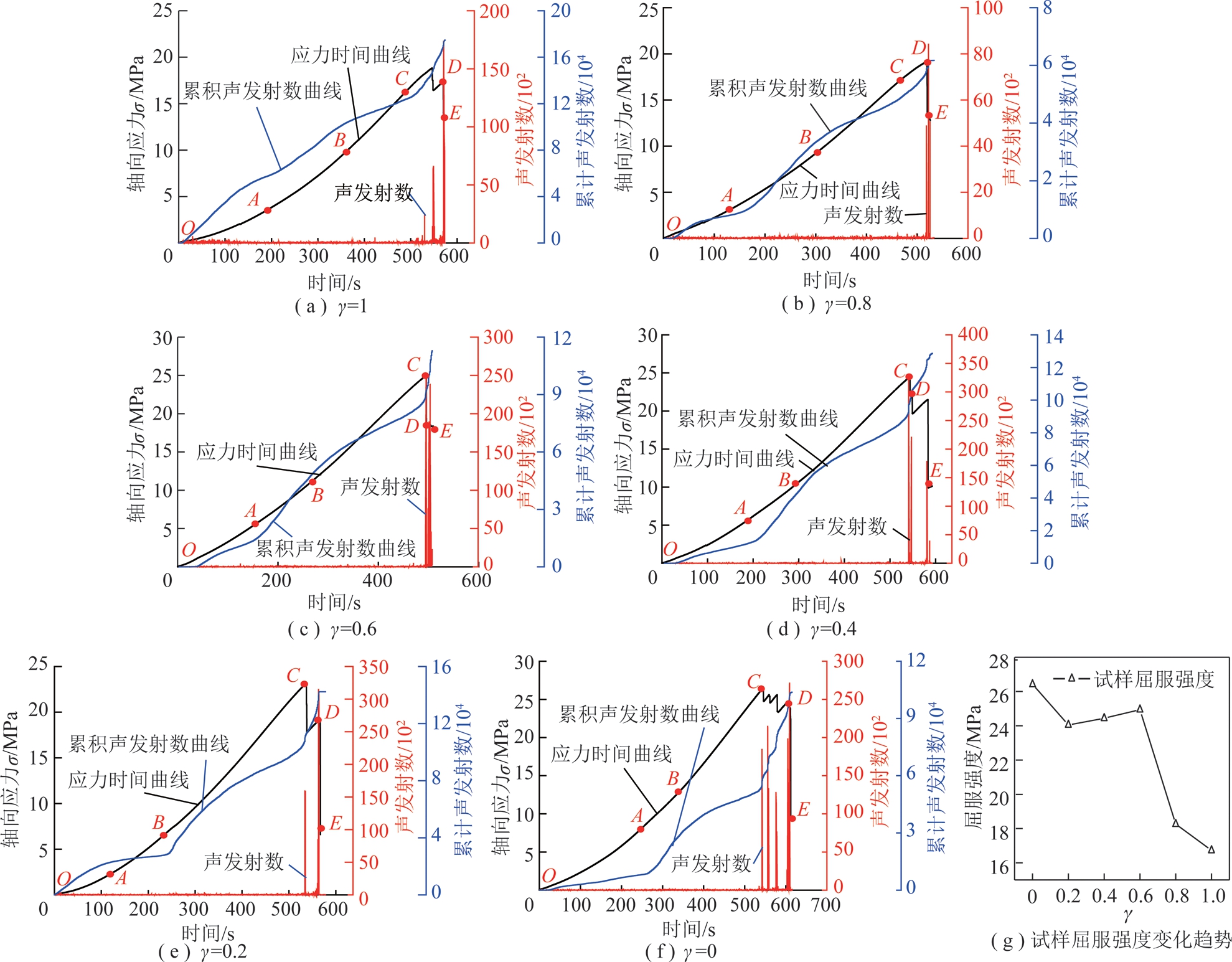
图5 不同γ值试样声发射分布特征和屈服强度
Fig.5 AE distribution characteristics and yield strength
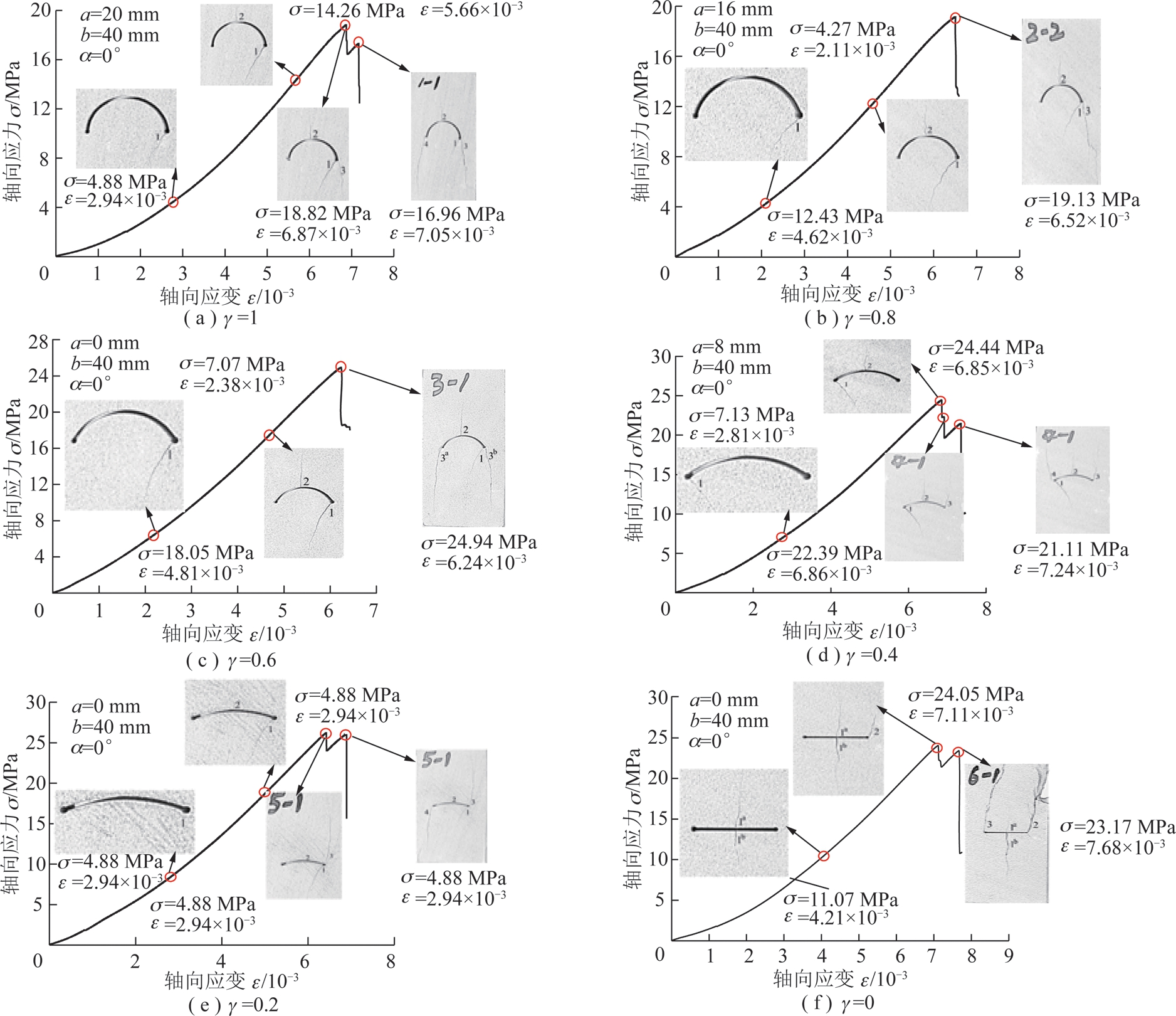
图6 不同γ值试样破裂演化过程
Fig.6 Fracture evolution process of the sandstone samples
图5(g)表明试样屈服强度随γ增大呈现先减小后缓慢增大最后又急剧减小趋势，γ=1试样屈服强度最小为16.72 MPa，γ在0.2～0.6试样屈服强度趋于稳定，γ在0.6～0.8试样屈服强度陡然减小，其强度由24.94 MPa降至18.26 MPa，下降了6.68 MPa，降幅为26.78%。γ=0时试样屈服强度达到最大值为26.42 MPa。可见，在单轴压缩作用下γ对试样的屈服强度也具有重要影响作用。
从弧形裂隙缺陷砂岩初始破坏形式可知，试样的破坏主要是从裂隙一侧尖端处发起，随后弧形顶部中间位置处产生纵向拉伸裂隙。随着轴向应力增加，次生尖端拉伸裂纹萌生并且持续扩展，次生裂纹与自由面贯通导致试样整体结构破坏，如图6所示。由于篇幅原因，本文仅选取γ =1的试样对弧形裂隙缺陷砂岩试样的破裂演化特征进行分析。
在轴向压力达到4.88 MPa，对应的轴向应变为2.94×10-3时，预制弧形裂隙右侧尖端处出现细微的拉伸裂纹1，并伴随较为强烈的声发射现象，尖端处拉伸裂纹1的扩展范围如图6(a)所示。当轴向应力达到14.26 MPa，对应的轴向应变为5.66×10-3时，拉伸裂纹1持续扩展，同时弧形预制裂纹拱顶出现平行于加载方向的微小拉伸裂纹2，左侧尖端出现轻微剥落现象并伴随强烈的声发射现象，但应力并未跌落。当轴向应力达到峰值强度18.82 MPa，对应的轴向峰值应变为6.87×10-3时，裂纹1和2继续扩展，预制裂隙的右侧尖端出现张拉裂纹3，随后轴向应力由18.82 MPa跌落至16.48 MPa。当轴向应力达到16.96 MPa时，对应轴向应变为7.05×10-3时，裂纹1宽度出现开度变窄现象，裂纹2并未出现持续扩展，这种现象是由于处于同一承载结构中的裂纹3的持续扩展和新的张拉裂纹4的出现造成。随着轴向应力的增大，拉伸裂纹3和裂纹4与试样自由面贯通，试样整体失去稳定导致最终破坏。
通过试样破裂演化特征可知，预制弧形裂隙的破坏大部分是从底部尖端脆弱区发起，分析原因是由于该处是应力集中区，当应力大于其抗拉强度时，该处产生微小的张拉裂纹。随着轴向应力增大，弧形裂纹拱顶部位出现张拉裂纹。但试样的最终破坏并不是由初始尖端裂纹和非尖端裂纹的扩展所致，而是由次生尖端裂纹的扩展并与自由面贯通造成。γ的不同对弧形裂隙缺陷试样的破坏形式具有重要影响，γ越大，试样内弧形裂纹尖端处越容易产生张拉裂纹。
2.3.2 初始起裂形式与起裂应力
岩石材料具有非均质、非连续及各向异性特点，在加载过程中会出现局部应力集中，当应力超过该区域的材料强度时，就会发生开裂破坏[18]。试样在加载过程中的起裂位置和起裂应力能够反映岩石材料的非均质性和内部缺陷的结构性。表1给出了试样的初始起裂应力、起裂时的应变及初始起裂位置。可以看出预制弧形裂隙缺陷砂岩在单轴压缩作用下，初始起裂是以弧形裂隙尖端处的拉伸破坏开始为主，出现一条与加载方向具有一定夹角的初始裂纹，随后在弧形拱顶出现非尖端拉伸裂纹。随着轴向应力的增大，裂纹逐渐扩展同时出现次生裂纹，次生裂纹扩展并与自由面贯通导致试样出现整体失稳破坏。
表1 试样起裂应力应变和起裂位置
Table 1 Stress and the position of the initial fracture of sandstone
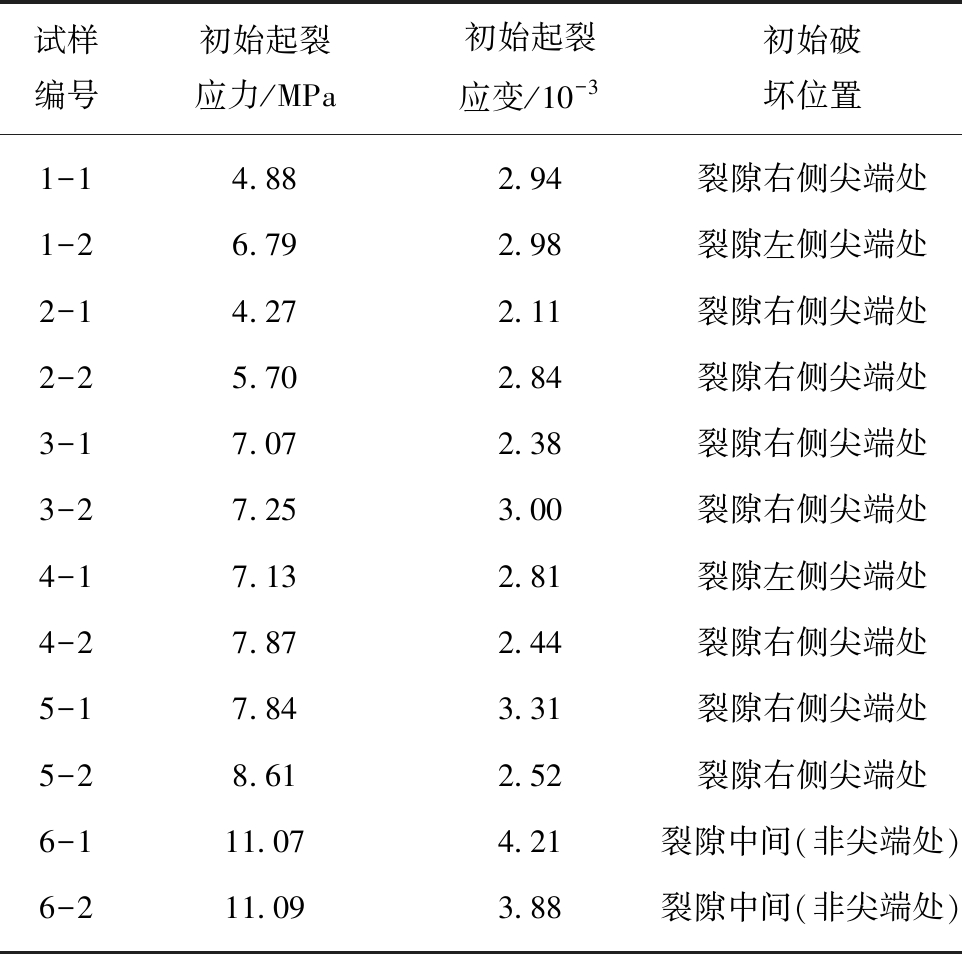
试样编号初始起裂应力/MPa初始起裂应变/10-3初始破坏位置1-14.882.94裂隙右侧尖端处1-26.792.98裂隙左侧尖端处2-14.272.11裂隙右侧尖端处2-25.702.84裂隙右侧尖端处3-17.072.38裂隙右侧尖端处3-27.253.00裂隙右侧尖端处4-17.132.81裂隙左侧尖端处4-27.872.44裂隙右侧尖端处5-17.843.31裂隙右侧尖端处5-28.612.52裂隙右侧尖端处6-111.074.21裂隙中间(非尖端处)6-211.093.88裂隙中间(非尖端处)
由图7(a)可知，γ值对试样起裂应力具有重要的影响作用，随着γ值的增大，试样起裂应力呈总体减小趋势，γ=0.8时试样的平均起裂应力最小，其值为4.99 MPa，表明该试样最容易发生初始破坏。γ=0时试样的平均起裂应力值为11.08 MPa，平均起裂应力值最大。其中，γ值在0～0.2，平均起裂应力值由11.08 MPa降至8.23 MPa，降低了2.85 MPa，降低幅度达25.72%。γ=0.2～0.6，平均起裂应力由8.23 MPa降至7.15 MPa，降低了1.08 MPa，降幅为13.12%，由此可见，试样的γ在该范围内，起裂应力值变化并不明显，对试样初始破坏影响较小。γ=0.6～0.8，平均起裂应力出现先减小后增大趋势。由图7(b)可以看出γ值对试样起裂应变也具有重要的影响，试样相应起裂应变与起裂应力变化趋势基本一致也呈现出先减小后增大的波动趋势，γ=0.8时试样的平均起裂应变最小，其值为2.48×10-3。
2.3.3 试样破坏形态分析
由图8可以看出，试样的最终破坏模式以拉伸破坏为主,图8中，T为拉伸裂纹，S为剪切裂纹。通过图9(a)～(e)可以发现，试样破坏大部分是从应力集中区的弧形尖端发起，试样在轴向应力达到起裂应力时，首先在一侧弧形尖端处产生与竖向应力有一定夹角的微小拉伸裂纹1，随着轴向应力的增大，拉伸裂纹1持续扩展且开度增大，同时弧形裂隙弧顶出现拉伸裂纹2。在应力达到一定强度时，裂隙尖端处顺序出现较大拉伸裂纹3和4，在裂纹3和4扩展的过程中裂纹1开度变小。试样最后的破坏是裂纹3和4与自由面的贯通造成的拉伸破坏。试样在破坏的瞬间释放的大量弹性能导致岩块出现折断现象，如图8(a)～(c)和(e)～(f)在试样破坏的过程中出现了1～2个的折断破坏现象，然而图8(d)试样在失去承载能力时并未发生明显的折断现象，破坏后的试样较为完整。
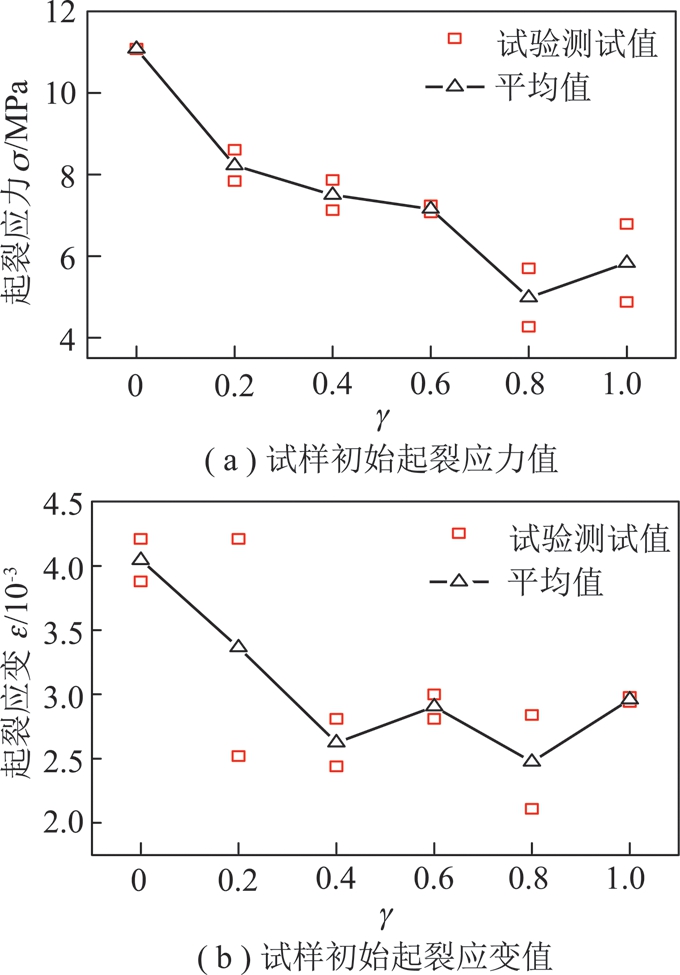
图7 预制弧形裂隙单轴压缩下起裂应力值和应变值
Fig.7 Crack initiation stress and the strain of sandstone samples
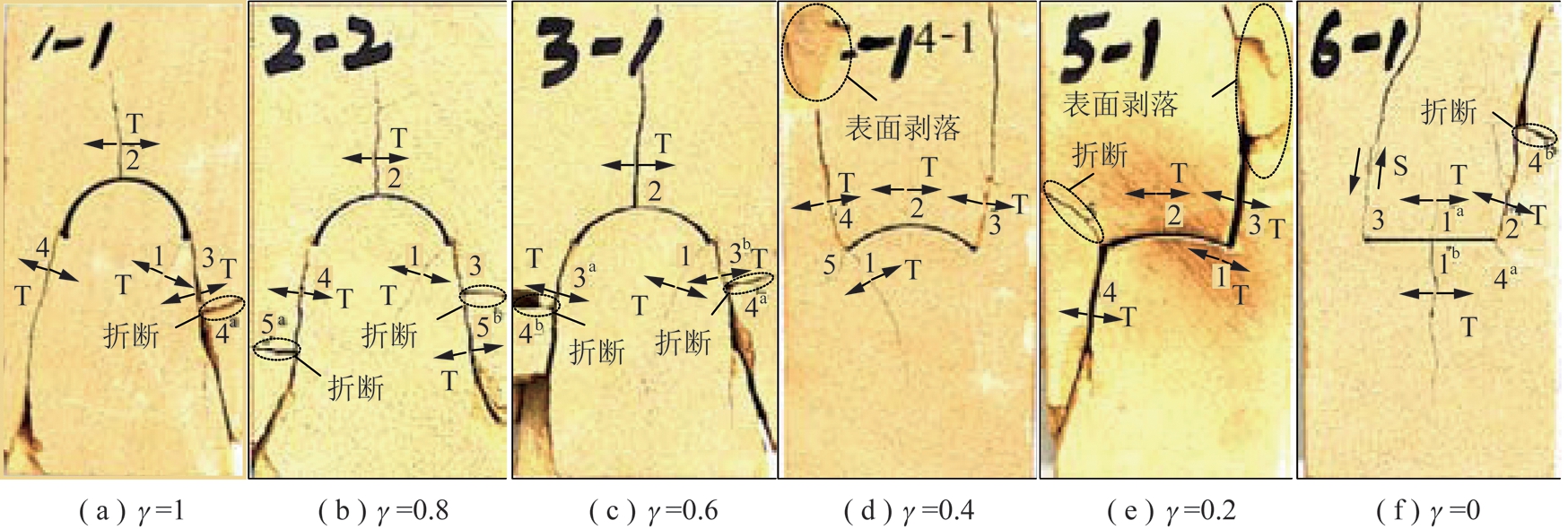
图8 不同γ值试样破坏形态
Fig.8 Failure mode of the sandstone samples
图8(f)即γ=0的试样表明初始拉伸裂纹1a和1b同时萌生于直线型预制裂隙的中间位置处，裂纹1a和1b在裂隙两侧呈对称分布，并且均近似平行于竖直加载方向。在轴向应力达到峰值强度时，裂隙右侧尖端处出现拉伸裂纹2，同时出现应力跌落现象并伴随巨大声发射事件。随着轴向加载的持续，拉伸裂纹2与自由面贯通，同时裂隙左侧尖端处发生剪切破坏产生裂纹3，可见γ=0的试样破坏模式为拉剪混合破坏。
3 裂纹扩展力学机制探讨
任一种类型裂纹端部应力场分布规律是相同的[27]，其大小仅取决于应力强度因子KJ。因此本文通过建立如图9所示弧形裂隙的力学模型来确定弧形裂隙尖端应力强度因子，该物理量可以表征裂纹端部应力场强弱以及断裂韧性大小。假设黄砂岩中任意Z0点受集中荷载作用，预制圆弧形裂纹Z1Z2的圆心角为2β，弧形裂隙的半径为r。弧形裂隙周围应力场中可通过构建黎曼-希尔伯特问题后用标准复变函数法进行求解[28]。
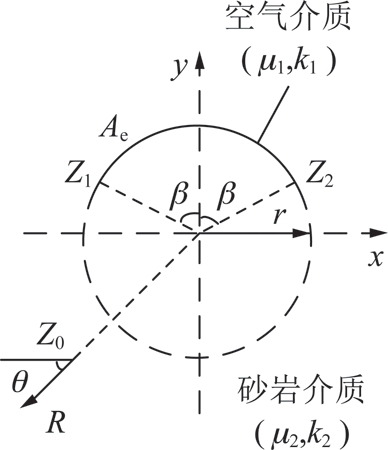
图9 集中荷载作用下弧形裂隙
Fig.9 Arc crack under concentrated load
可建立Kolosov-Muskhelishvili表达式如下:
(1)
(2)
(3)
式中，Wj(z)为裂隙尖端应力复数表达式；W′j(z)为Wj(z)一阶导数；σrr和σθθ分别为砂岩介质任一点的径向正应力和环向正应力；τrθ为砂岩介质任一点的剪应力；i为虚数单位；uj和vj为砂岩介质某点位移分量；μj为介质泊松比；z为岩石材料中任意一点位置的复数表达形式;
为z的共轭复数;kj=(3-vj)/(1+vj)为砂岩平面应力;kj=(3-4vj)为试样平面应变，引入下式
(4)
则可以证明:
(5)
式中，r为质点到坐标原点的距离。
因为裂缝面无附着摩擦力从而引入了下面的黎曼-希尔伯特问题:
在
上)
(6)
在
上)
(7)
弧形裂隙两介质交界面结合部分的应力和位移连续性需满足如下要求:
在Ab上)
(8)
在Ab上)
(9)
式中，μ1，μ2分别为空气和砂岩介质的泊松比； k1，k2分别为空气和砂岩介质的平面应力及平面应变。
Ac和Ab分别对应于2种介质交界面的开裂部分和黏结部分，式(8)和(9)可被视为在交界面结合部分从S+到S-的解析延拓，因此W1(t)和Ω1(t)可以用W2(t)和Ω2(t)来表示，因此，对于黄砂岩介质内潜能为
[W2(t)-Ω2(t)]++α[W2(t)-Ω2(t)]-=
-2(1+α)(σrr+iτrθ)
(10)
[W2(t)+αΩ2(t)]+-[W2(t)+αΩ2(t)]-=0
(11)
式中，
以上黎曼-希尔伯特问题可通过方程(12)和(13)解决:
(12)
(13)
式中，e0为常数；t1和t2分别为弧形裂隙两端的位置坐标；P0，P1，P2为罗朗展开式系数；P-1和P-2为与介质交界面法向相反的罗朗展开式系数。
式(13)中的χ(z)可由Plemelj方程解出:
(14)
上式中当z→
时，
另外，
χ(z)在z→0和z→处的展开式如下:
χ(z)=F10(1+zF12+z2F13+…),z→0
(15)
(16)
式中，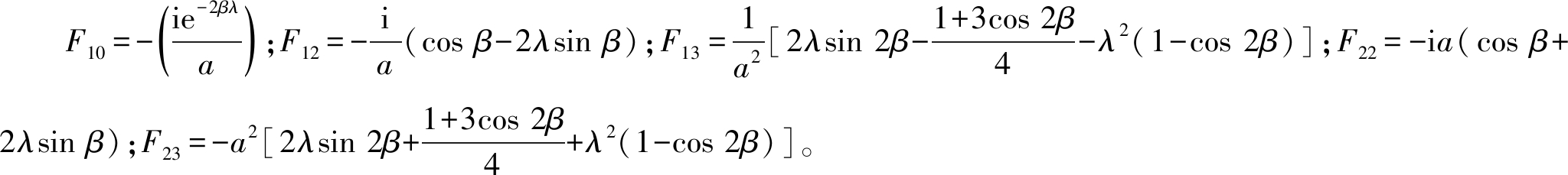
为了求解(13)中的积分，将线积分变形为远场围线积分法，可以观察到在原点、无穷大、z0和
处有极限，
其最终的解为
(17)
(18)
(19)
(20)
式中，
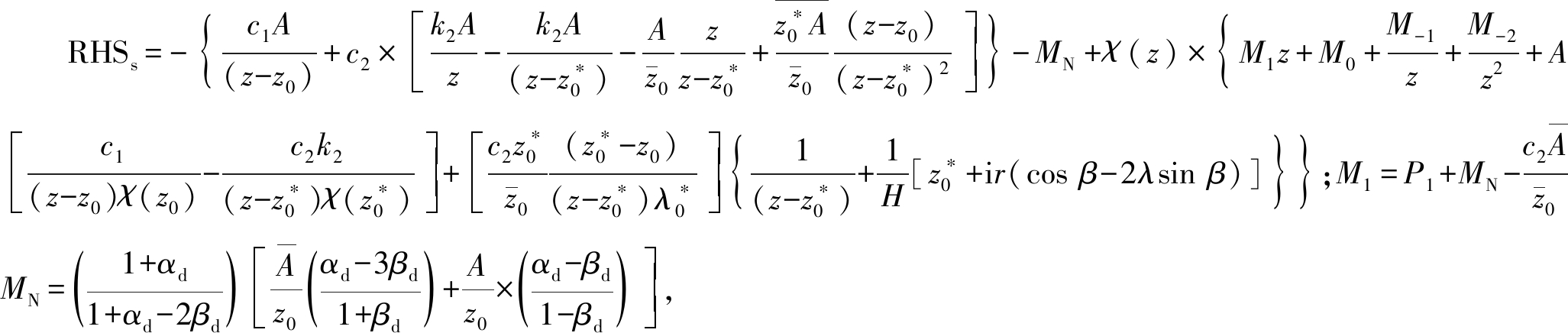其中,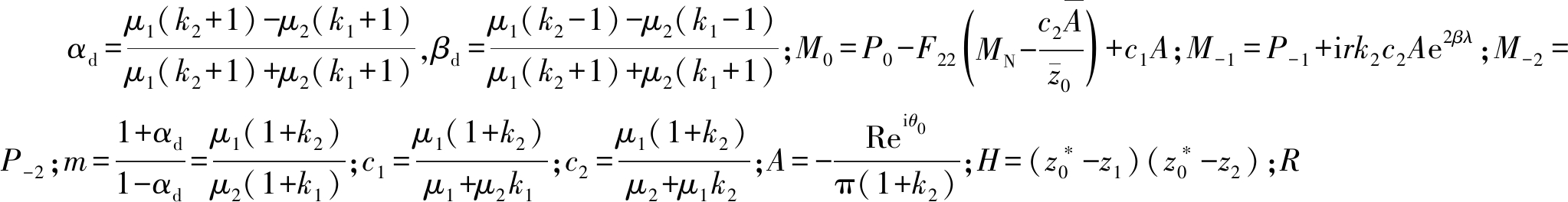
和θ0分别为点力在z0处的大小和方向。
e0,t1,t2,M1,M0,M-1和M-2七个常量是由原点和无穷大处求解所得。根据文献[29]定义了2种介质交界面裂纹的复应力强度因子为
(21)
其中，λ=-lg α/(2π)；i为虚数单位;z″对应于z1处的新坐标系，该坐标系通过z=eiβ(z″-ir)进行转换，如图10所示。通过式(17)可求得交界面裂纹的复应力强度因子为
(22)
式中，
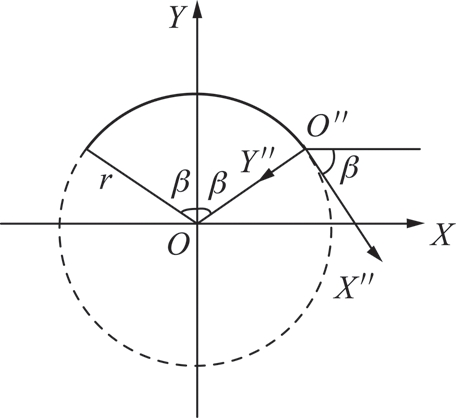
图10 经过转换后的新坐标系统O"
Fig.10 Transformation to the new coordinate system at O"
通过交界面复应力强度因子可以看出弧形裂隙夹角β和半径r影响裂隙尖端应力场分布，也是影响裂隙尖端起裂应力大小的重要因素，当γ =0→r=0 mm，β=0°;γ =0.2→r=52.0 mm，β=22.6°;γ=0.4→r=29.0 mm，β=43.5°;γ =0.6→r=22.67 mm，β=61.90°;γ =0.8→r=20.5 mm，β=77.3°;γ =1.0→r=20 mm，β=90°。把夹角β和半径r代入式(22)可求出不同γ下的应力强度因子，由图11可知，通过应力强度因子数值拟合曲线可以看出应力强度因子随γ增大呈逐渐减小趋势，这与试验测得的初始起裂应力和应变值的变化趋势基本吻合，表明弧形预知裂隙γ值越大尖端断裂韧性越小，试样越容易起裂。
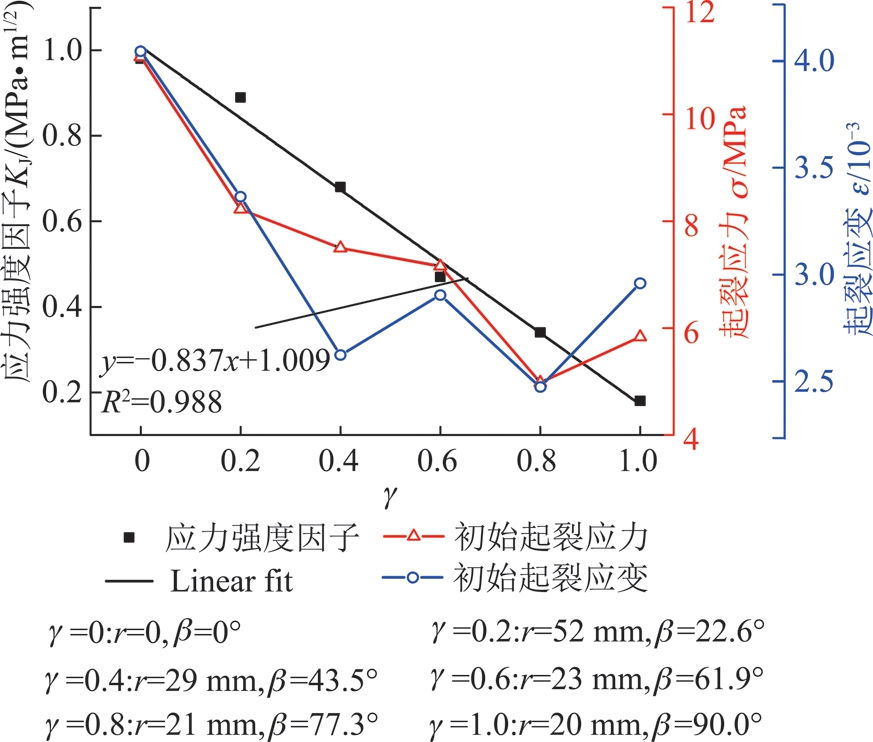
图11 应力强度因子变化趋势
Fig.11 Change trend of stress intensity factor
4 结 论
(1)弧形裂隙缺陷砂岩试样随着γ的增大，峰后试样的承载能力逐渐降低，试样峰值强度、平均模量和割线模量出现总体减小趋势。在γ=0～0.6峰值强度劣化程度处于稳定状态，当γ为0.6～0.8时峰值强度劣化程度加剧，γ为1时，试样峰值强度最小，这也表明γ在0.6～1.0对试样峰值强度的改变影响因素最为显著。
(2)随着γ值的增大累计声发射数呈整体减小趋势，γ为0.8时，累计声发射事件数最小，γ为0.2时，累计声发射事件数最大。γ值对试样起裂应力具有重要的影响作用，随着γ值的增大，试样起裂应力呈总体减小趋势，γ=0.8时平均起裂应力值最小，试样最容易发生初始破坏;γ=0时，试样的平均起裂应力值最大，其值为11.08 MPa。试样相应起裂应变也呈现出先减小后增大的波动趋势。当γ=0时初始起裂裂纹萌生于直线型裂隙的中间位置;当γ=0.2～0.8时，裂纹萌生于预制裂隙尖端位置处。
(3)随着γ的增大，试样的破坏模式由拉剪混合破坏向拉伸破坏转变，当γ=0时，试样为拉剪破坏;当γ在0.2～1.0时，试样为拉伸破坏。初始起裂裂纹扩展并不是导致试样最终破坏的原因，次生裂纹的扩展与自由面贯通才是导致试样整体破坏原因，试样破坏瞬间释放大量弹性能导致岩块折断和表面剥落现象。通过对含弧形裂隙裂纹扩展机制探讨推导出应力强度因子表达式，并根据该表达式求出相应应力强度因子值，曲线拟合后发现其变化趋势与试验值变化趋势基本吻合。
本文仅针对含弧形预制裂隙的γ对砂岩力学特征和破裂演化过程进行了研究，为了充分研究非直线型裂隙的对岩石力学影响，未来将通过改变加载方式和利用数值模拟等手段深入研究该含该类缺陷岩石的力学特征。
[1] PRUDENCIO M,JAN M V S.Strength and failure modes of rock mass models with non-persistent joints[J].International Journal of Rock Mechanics & Mining Sciences,2007,44(6):890-902.
[2] 李宁,陈文玲,张平.动荷作用下裂隙岩体介质的变形性质[J].岩石力学与工程学报,2001,20(1):74-78.
LI Ning,CHEN Wenling,ZHANG Ping.Deformation properties of jointed rock mass under dynamic cyclic loading[J].Chinese Journal of Rock Mechanics & Engineering,2001,20(1):74-78.
[3] 张平.裂隙介质静动应力条件下的破坏模式与局部化渐进破损模型研究[D].西安:西安理工大学,2004.
ZHANG Ping.Research on failure modes and localized progressive failure model of the cracked media under static and dynamic stress conditions[D].Xi’an :Xi’an University of Technology,2004.
[4] 韩观胜,靖洪文,苏海健,等.预制双圆形孔洞砂岩强度与变形破坏特征[J].煤炭学报,2017,42(4):871-878.
HAN Guansheng,JING Hongwen,SU Haijian,et al.Experimental study on compressive strength and fracture characteristics of sandstone containing double circular cavities[J].Journal of China Coal Society,2017,42(4):871-878.
[5] FAN L F,WU Z J,WAN Z,et al.Experimental investigation of thermal effects on dynamic behavior of granite[J].Applied Thermal Engineering,2017,125:94-103.
[6] 靳瑾,曹平,蒲成志.预制裂隙几何参数对类岩材料破坏模式及强度的影响[J].中南大学学报(自然科学版),2014,45(2):529-535.
JIN Jin,CAO Ping,PU Chengzhi.Influence of flaw parameters on damage mode and strength of rock-like materials[J].Journal of Central South University,2014,45(2):529-535.
[7] 郑文翔,赵延林,王敏.单轴压缩条件下预制裂隙类岩石材料试验研究[J].湖南科技大学学报(自然科学版),2013,28(4):1-6.
ZHENG Wenxiang,ZHAO Yanlin,WANG Min.Experimental study on rock-like material with pre-cracks under uniaxial compression[J].Journal of Hunan University of Science & Technology,2013,28(4):1-6.
[8] 李术才,李廷春,王刚,等.单轴压缩作用下内置裂隙扩展的CT扫描试验[J].岩石力学与工程学报,2007,26(3):484-492.
LI Shucai,LI Tingchun,WANG Gang,et al.CT real-time scanning tests on rock specimens with artificial initial crack under uniaxial conditions[J].Chinese Journal of Rock Mechanics & Engineering,2007,26(3):484-492.
[9] 杨圣奇,戴永浩,韩立军,等.断续预制裂隙脆性大理岩变形破坏特性单轴压缩试验研究[J].岩石力学与工程学报,2009,28(12):2391-2404.
YANG Shengqi,DAI Yonghao,HAN Lijun,et al.Uniaxial compression experimental research on deformation and failure properties of brittle marble specimen with pre-existing fissures[J].Chinese Journal of Rock Mechanics & Engineering,2009,28(12):2391-2404.
[10] 肖桃李,李新平,贾善坡.含2条断续贯通预制裂隙岩样破坏特性的三轴压缩试验研究[J].岩石力学与工程学报,2015,34(12):2455-2462.
XIAO Taoli,LI Xinping,JIA Shanpo.Failure characteristics of rock with two pre-existing transfixion cracks under triaxial compression[J].Chinese Journal of Rock Mechanics & Engineering,2015,34(12):2455-2462.
[11] 林恒星,朱珍德,孙亚霖,等.透明类岩石预制裂隙不同赋存方式起裂扩展研究[J].固体力学学报,2015,36(10):58-64.
LIN Hengxing,ZHU Zhende,SUN Yalin,et al.Experimental studies on pre-existing crack in different ways propagation and coalescence in transparent rock[J].Chinses Journal of Solid Mechanics,2015,36(10):58-64.
[12] 蒲成志.单轴压缩下类岩体裂隙材料断裂破坏机制的试验研究[D].长沙:中南大学,2010.
PU Chengzhi.Experiment research on the fracture failure mechanism of rock-like material with fissures under uniaxial compression[D].Changsha:Central South University,2010.
[13] NEMAT-NASSER S,HORII H.Compression-induced nonplanar crack extension with application to splitting,exfoliation,and rockburst[J].Journal of Geophysical Research Solid Earth,1982,87(B8):6805-6821.
[14] WONG R H C,CHAU K T,TANG C A,et al.Analysis of crack coalescence in rock-like materials containing three flaws—Part I:Experimental approach[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(7):909-924.
[15] WONG R H C,CHAU K T.Crack coalescence in a rock-like material containing two cracks[J].International Journal of Rock Mechanics and Mining Sciences,1998,35(2):147-164.
[16] 杨圣奇.断续三裂隙砂岩强度破坏和裂纹扩展特征研究[J].岩土力学,2013,34(1):31-39.
YANG Shengqi.Study of strength failure and crack coalescence behavior of sandstone containing three pre-existing fissures[J].Rock & Soil Mechanics,2013,34(1):31-39.
[17] YANG S Q.Crack coalescence behavior of brittle sandstone samples containing two coplanar fissures in the process of deformation failure[J].Engineering Fracture Mechanics,2011,78(17):3059-3081.
[18] YANG S Q,LIU X R,JING H W.Experimental investigation on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression[J].International Journal of Rock Mechanics & Mining Sciences,2013,63(5):82-92.
[19] 熊飞,靖洪文,苏海健,等.尖端相交裂隙砂岩强度与破裂演化特征试验研究[J].煤炭学报,2017,42(4):886-895.
XIONG Fei,JING Hongwen,SU Haijian,et al.Strength and fracture behaviors of sandstone samples containing intersect fissures under uniaxial compression[J].Journal of China Coal Society,2017,42(4):886-895.
[20] NGUYEN T L,HALL S A,VACHER P,et al.Fracture mechanisms in soft rock:Identification and quantification of evolving displacement discontinuities by extended digital image correlation[J].Tectonophysics,2011,503(1/2):117-128.
[21] YIN P,WONG R H C,CHAU K T.Coalescence of two parallel pre-existing surface cracks in granite[J].International Journal of Rock Mechanics & Mining Sciences,2014,68(6):66-84.
[22] XIE H P，LIU J F,JU Y,et al.Fractal property of spatial distribution of acoustic emissions during the failure process of bedded rock salt[J].International Journal of Rock Mechanics and Mining Sciences，2011，48(8):1344-1351.
[23] MA G W,DONG Q Q,FAN L F,et al.An investigation of non-straight fissures cracking under uniaxial compression[J].Engineering Fracture Mechanics,2018，191:300-310.
[24] 纪洪广，卢翔.常规三轴压缩下花岗岩声发射特征及其主破裂前兆信息研究[J].岩石力学与工程学报，2015，34(4):694-702.
JI Hongguang，LU Xiang.Characteristics of acoustic emission and rock fracture precursors of granite under conventional triaxial com-pression[J].Chinese Journal of Rock Mechanics and Engineering，2015，34(4):694-702.
[25] 孙强,薛雷.砂岩脆性破坏过程中声发射信息试验研究[J].固体力学学报,2012,33(5):541-547.
SUN Qiang,XUE Lei.Research on AE variation of sandstone brittle failure with along loading by uniaxial compression[J].Chinese Journal of Solid Mechanics,2012,33(5):541-547.
[26] MARTIN C D.The strength of massive Lac du Bonnet granite around underground openings[D].Manitoba:University of Manitoba,1993.
[27] 李世愚,和泰名,尹祥础.岩石断裂力学[M].北京:科学出版社,2015.
[28] PRASAD P B N,SIMHA K R Y.Interface crack around circular inclusion:SIF,kinking,debonding energetics[J].Engineering Fracture Mechanics,2003,70(2):285-307.
[29] RICE J R,SIH G C.Plane problems of cracks in dissimilar media[J].Journal of Applied Mechanics,1965,32(2):418-423.
