
移动阅读
充填采矿法是将矿业固废(尾砂、废石)与适量胶凝材料混合后回填至采空区,为地下采矿提供安全作业平台并管控地压等,实现一废治两害的绿色采矿法。随着对矿山安全和环保意识的不断提高以及对矿产资源回收率的日益重视,充填采矿法近年来获得了巨大发展和广泛应用。其中,阶段空场嗣后充填采矿法是充填法与空场法的有机结合,在继承充填法优点的同时,兼有空场法的生产效率高、回采强度大和作业环境安全等优点,是目前生产效率最高的充填采矿法,代表了大规模高效率绿色清洁采矿的发展方向[1]。
阶段空场嗣后充填采矿法一般将矿体间隔划分为矿房、矿柱采场:首先回采一步骤矿房采场,出矿完成后胶结充填采场空区,该胶结充填体作为竖直人工矿柱有利于改善采场地压环境,并为后续二步骤矿柱采场的回采提供安全保护;一步骤矿房采场胶结充填体达到预期强度后,依次回采相邻的二步骤矿柱采场,出矿后一般非胶结充填二步骤采场空区,降低充填成本。
该采矿法的采充过程中,一步骤采场胶结充填体侧向揭露后的稳定性是二步骤采场矿石能否安全回采的关键。为此,须在一步骤采场充填时添加适量胶凝材料(一般为水泥),以满足人工充填矿柱的强度要求和揭露稳定性。但由于矿山采场空间的胶结充填对胶凝材料消耗量巨大,使胶充成本一般占矿山充填作业总成本的70%~80%以上,并至少占矿山运营总成本的10%~20%[2-4]。因此,合理确定一步骤采场胶结充填体的最优强度需求是有效平衡该采矿法安全和成本的关键。
20世纪80年代以前,国外通常采用两种方法确定该胶结充填体的强度需求:一是利用覆重法计算充填体自重应力(σv=γh,其中γ为充填体容重,h为从充填体上表面开计的埋深),此充填体所需单轴抗压强度(σc)只要满足σc≥σv=γh,得出充填体强度需求从充填体上表面的0线性增加至最底部γH(H为充填体竖向揭露总高度)[5];另一种是借鉴土力学滑坡法,源于黏性土质边坡竖向揭露后的稳定性研究,此时充填体所需单轴抗压强度满足σc≥γH/2,该法计算得出的充填体强度需要充填体自上表面至底部是均匀的[6]。但这2种方法均是二维平面模型,忽略了充填体与采场围岩的接触作用,而且没有考虑充填体自身的强度性质,导致得出的充填体强度需求过于保守,进而引起矿山胶充成本虚高[5]。
为此,加拿大MITCHELL等[5]考虑了采场侧壁围岩与胶结充填体的接触黏结作用,构建了单侧竖向揭露胶结充填体的三维楔形滑动模型,用于胶结充填体强度需求计算。该模型后被国外采矿工业界和学术界普遍应用,降低了充填采矿胶充成本[7-8]。近期,加拿大LI等[9-11]进一步考虑采场尺寸、充填体内摩擦角、充填体与采场围岩摩擦作用、充填体破坏模式等因素,对原始Mitchell模型[5]进行了修正发展。
然而,以上的强度需求解析模型[5,9-11]主要是针对单个孤立的胶结充填体(1个侧面竖向揭露,另3个竖向侧面与采场围岩接触),均未考虑实际采充过程中二步骤采场非胶结充填体对相邻一步骤采场胶结充填体的侧压作用。对此,LIU等[12]从阶段空场嗣后充填法的采充时序出发,研究了非胶结充填体侧压作用对胶结充填体稳定性影响,修正了胶结充填体强度需求解析模型与方法。
针对阶段空场嗣后充填法采场充填体强度需求的确定问题,国内一方面采用同类矿山的经验类比法或经验公式法,或借鉴国外的简化公式,估算充填体强度需求指标[13-14]。另一方面,相关学者结合充填体力学特征,探索了充填体强度需求与围岩的匹配关系,如刘志祥等[15-17]测试分析了胶结充填体的损伤变形特征,基于岩体开挖能量释放与充填体能量蓄积相近的假设,获取了与围岩不同应力条件相匹配的充填体强度需求。此外,国内学者将混沌优化理论、可靠度理论等引入充填体强度需求研究中,探索了充填采矿的不确定因素、采场充填体实际强度分布的复杂非线性特征对充填体强度需求的影响[18-19]。
值得注意的是,国内外充填体强度需求计算模型中,大多数强调了采场充填体与周边介质(围岩、充填体)的力学接触作用重要性。国外主要基于Marston模型[20]计算充填体二维成拱应力,进而确定充填体与围岩的摩擦接触边界[5,7-12]。国内则基于能量等效传递假设[15-17],考虑充填体与围岩接触作用对胶结充填体强度计算的影响。而LIU等[12]不仅考虑了充填体与围岩接触作用后的二维拱应力,还考虑了非胶结充填体对相邻胶结充填体的接触侧压作用,研究设计充填体强度需求。但在LIU等[12]的强度修正模型中,非胶结充填体的侧压作用是按各向相等的自重应力假设(非胶结充填料浆处于静水压力状态,相对简单且保守),主要适用于排水性能较差的膏体充填体(细粒多)在充填完成早期的侧压作用计算[21-22],而且胶结充填体的拱应力也是基于二维Marston解析模型。采场充填体与周边介质的力学接触作用均是采用二维模型或假设。
然而,实际采场胶结充填体在侧向揭露时大多处于固结排水后的长期强度状态,其拱应力分布是处于三维状态。如何计算二步骤采场非胶结充填体在三维成拱状态下的应力分布及其对相邻胶结充填体的侧压作用,如何计算单侧揭露后胶结充填体的三维拱应力及其与侧壁围岩的接触摩擦边界,又如何将非胶结充填体-胶结充填体-采场围岩之间的接触力学边界应用至胶结充填体的强度需求三维解析模型,目前国内外都尚未解决,但这些因素又会对采场充填体强度需求设计产生重要影响,笔者将针对这些问题展开论述。
由于充填体与围岩的强度刚度差异大,导致自重作用下采场充填体产生不同程度成拱作用,影响充填体应力分布[23-24],进而影响其揭露稳定性[25]。因此,获取可靠的充填体应力分布状态是研究设计单侧揭露胶结充填体强度需求的前提。
充填体应力拱作用是借鉴土力学土拱理论,原理上均描述相对松软介质受相对坚硬限制结构的接触摩擦作用,引起松软介质的部分自重应力转移至坚硬限制结构中的力学现象,表现为松软介质中不同埋深处的实际应力值低于同一深度的上覆层自重应力。该模型在土力学领域有较多探索应用,如抗滑桩间土体[26]、挡土墙后土体[27]、砂仓物料[28]应力模型。采场充填体原位应力监测证实了采场充填体应力成拱作用的存在[21,29]。
借鉴土力学领域Marston法[20],参考LI[30]和PIRAPAKARAN[31]对Marston法的修正研究,构建了如图1所示的二步骤采场非胶结充填体三维拱应力模型。与以往模型不同的是:图1模型结合了两步骤空场嗣后充填法的采充时序过程、相邻采场充填体之间及充填体与围岩之间的接触关系,考虑了非胶结充填体两竖向侧面受上下盘围岩夹制(面F1u和F3u),同时另外两竖向侧面受相邻采场的胶结充填体夹制(面F2u和F4u)。
图1中非胶结充填体与上下盘围岩接触面分别为面F1u和面F3u(假设该接触面内摩擦角为δ1u=δ3u=δ13u=r13uφu);非胶结充填体与相邻采场胶结充填体接触面分别为面F2u和面F4u(假设该接触面内摩擦角为δ2u=δ4u=δ24u=r24uφu);φu(°)为非胶结充填体内摩擦角;r13u,r24u( [0,1])为接触面内摩擦角与非胶结充填体内摩擦角比例系数(受接触面粗糙度、风化程度影响);H(m),L(m),B(m)分别为采场高度、长度和宽度。
[0,1])为接触面内摩擦角与非胶结充填体内摩擦角比例系数(受接触面粗糙度、风化程度影响);H(m),L(m),B(m)分别为采场高度、长度和宽度。
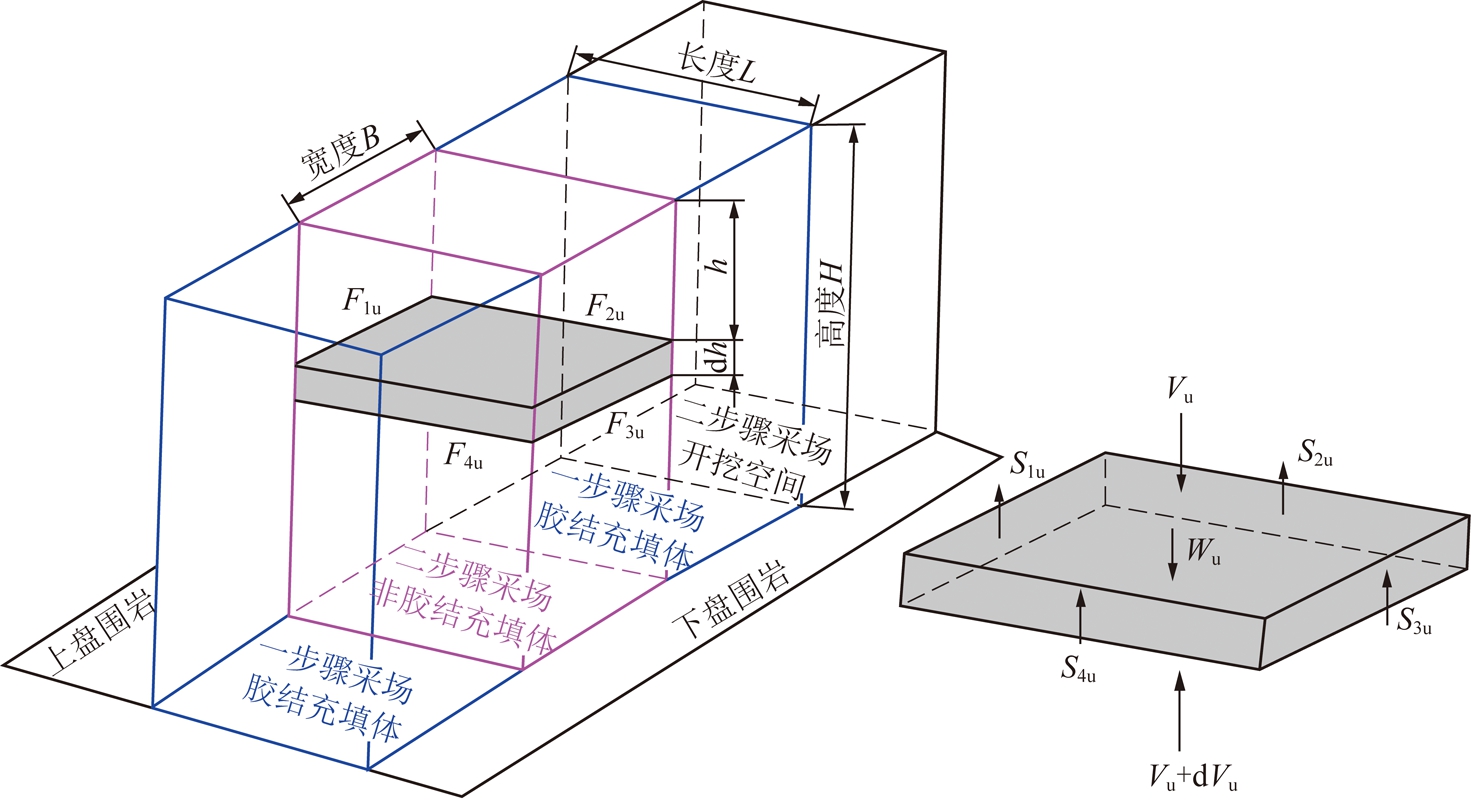
图1 二步骤采场非胶结充填体的拱应力解析模型
Fig.1 Analytical model of arching stress for uncemented backfill in secondary stope
在非胶结充填体任一埋深h处(自充填体上表面开始计算),选取充填体微分层单元(厚度为dh,m)。在非胶结充填体三维成拱作用下,假设该微分层单元的竖向正应力为σvu(kPa)、水平正应力为σhu(kPa),水平和竖向正应力可采用侧向土压力系数Ku换算(σhu=Ku σvu)。假设该微分层单元上表面受上覆充填体压力为Vu(kN),下表面受到下部充填体支撑力为Vu+dVu(kN)。非胶结充填体微分层单元的自重(kN)为Wu=γu LBdh(γu为非胶结充填体容重,kN/m3)。假设非胶结充填体与上下盘围岩接触面(面F1u和面F3u)、与相邻胶结充填体接触面(面F2u和面F4u)摩擦力(kN)分别为S1u,S3u,S2u,S4u。
根据图1中非胶结充填体微分层单元在竖直方向的静力平衡状态可得
Vu+Wu=Vu+dVu+S1u+S3u+S2u+S4u
(1)
假设非胶结充填体与上下盘围岩接触面的摩擦力相等S1u =S3u =S13u,非胶结充填体与相邻胶结充填体接触面的摩擦力相等S2u =S4u =S24u,则
Wu=dVu+2S13u+2S24u
(2)
Vu=σvuLB
(3)
S13u=τ13uBdh=σhuBdhtan δ13u=
K13uσvuBdhtan δ13u
(4)
S24u=τ24uLdh=σhuLdhtan δ24u=
K24uσvuLdhtan δ24u
(5)
将式(3)~(5)代入式(2),积分后可得式(6),用于非胶结充填体竖向应力σvu计算。
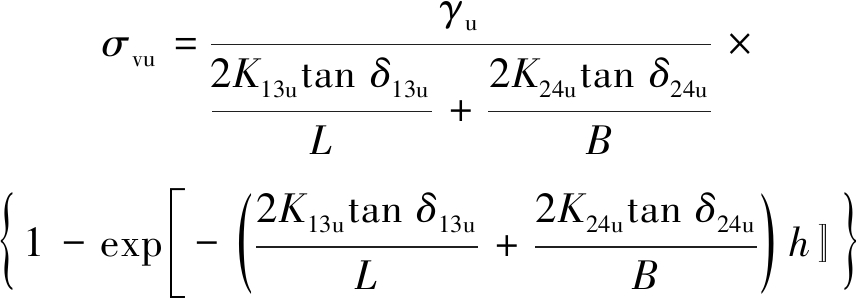
(6)
进一步假设图1中非胶结充填体微分层单元沿采场长度L方向和宽度B方向的侧向土压力系数相同(即K13u =K24u),推荐使用主动土压力系数[32],如式(7)所示。
K13u=K24u=Kau=tan2(45°-φu/2)
(7)
将式(7)代入式(6)后,可得图1非胶结充填体竖向正应力σvu(kPa)和水平正应力σhu(kPa)随埋深h变化关系计算方法,分别为式(8)和式(9):
![]()
(8)
![]()
(9)
以往的采场充填体拱应力解析模型大多基于土力学Marston模型(黏聚力为0),主要适用于非胶结充填体,而且模型中充填体的4个限制侧面均是围岩,不能分析单侧揭露后的胶结充填体拱应力状态。对此,构建了如图2所示的一步骤采场胶结充填体(揭露后)三维拱应力解析模型,其两竖向侧面与上下盘围岩接触(面F1c和面F3c,接触面黏聚力分别为c1c,c3c,内摩擦角分别为δ1c,δ3c),一个竖向侧面与相邻二步骤采场非胶结充填体接触(面F4c,该接触面剪切强度取决于非胶结充填体,接触面黏聚力为0,内摩擦角为δ4c=r4cφu=r24uφu),一个侧面竖向揭露(F2c,强度为0)。
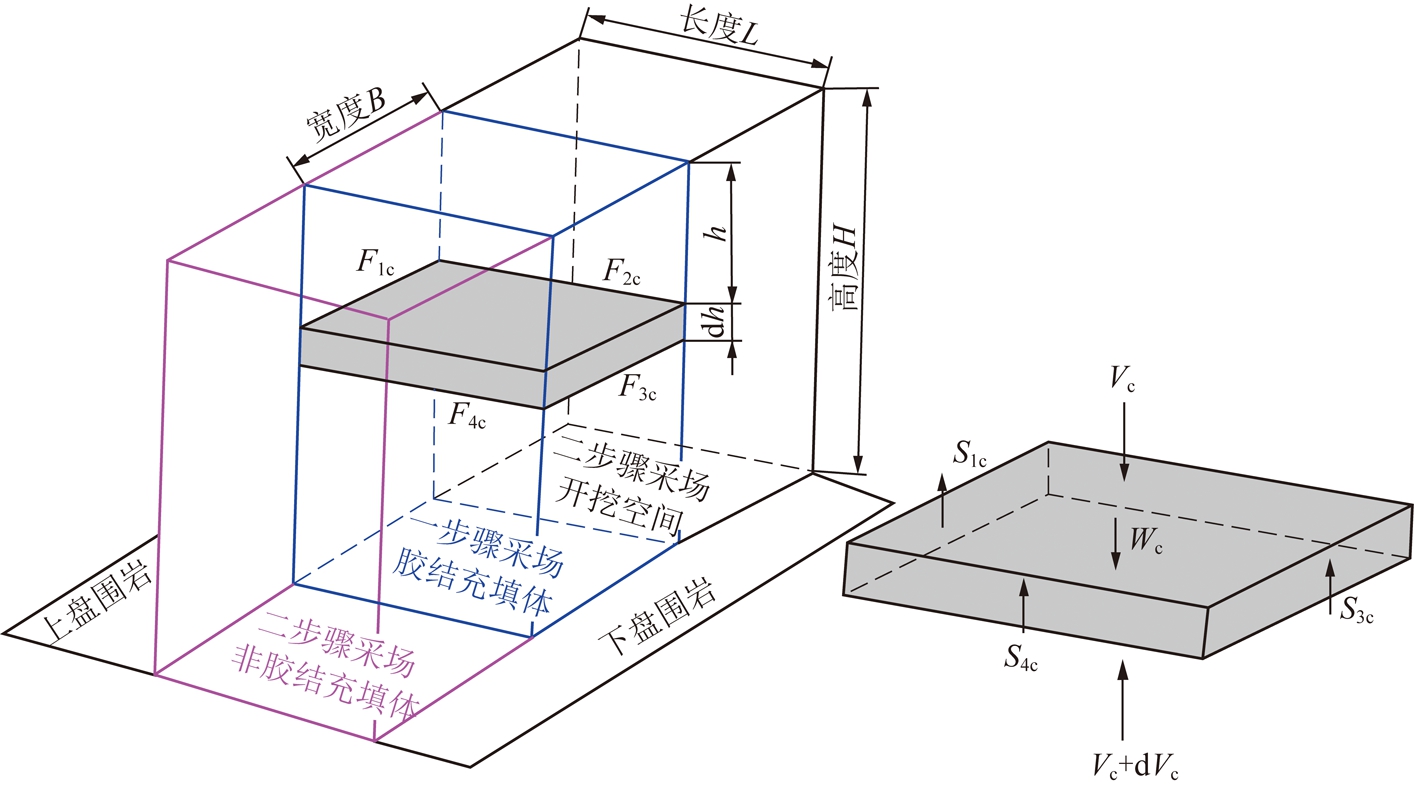
图2 一步骤采场胶结充填体拱应力解析模型(揭露后)
Fig.2 Analytical model of arching stress for vertically exposed cemented backfill in primary stope
考虑胶结充填体任一埋深h处的微分层单元(此处竖向和水平应力分别为σvc和σhc),微分层单元自重为Wc(kN),γc(kN/m3)是胶结充填体容重。微分层单元上表面受到上覆胶结充填体压力为Vc(kN),下表面受到下部充填体支撑力为Vc+dVc(kN)。胶结充填体与非胶结充填体接触面F4c上的摩擦力为S4c(kN),与上下盘围岩接触面F1c,F3c上的摩擦力沿竖直方向的分量(kN)分别为S1c,S3c,F2c面为相邻二步骤矿柱采场开挖后产生的自由面。
图2中单侧揭露后的胶结充填体微分层单元在竖直方向上的静力平衡方程为
Vc+Wc=Vc+dVc+S1c+S3c+S4c
(10)
假设胶结充填体与上下盘围岩接触面的剪切强度参数相同,得面F1c和面F3c的内摩擦角为δ1c=δ3c=δ13c=r13cφc,黏聚力为c1c=c3c=c13c=λ13ccc,其中φc(°)和cc(kPa)分别为胶结充填体内摩擦角和黏聚力。则式(10)可变换为
Wc=γcLBdh=dVc+2S13c+S4c
(11)
Vc=σvc LB
(12)
S13c=τ13cBdh=(c13c+σhctan δ13c)Bdh=
(λ13ccc+K13cσvctan δ13c)Bdh
(13)
S4c=τ4cLdh=σhcLdhtan δ4c=
K4cσvcLdhtan δ4c
(14)
将式(12)~(14)代入式(11)后积分求解,公式变换后得出单侧揭露后的一步骤采场胶结充填体竖向正应力σvc随埋深h计算公式:
![]()
(15)
式(15)中假设胶结充填体各接触面的侧向土压力系数相同,推荐主动土压力系数计算公式(16),进而得出单侧揭露后的一步骤采场胶结充填体水平正应力σhc计算方法,如式(17)所示。
Kc=K13c=K4c=Kac=tan2(45°-φc/2)
(16)
![]()
(17)
FLAC3D是一种基于显式拉格朗日计算方案的三维有限差分软件,根据采矿与岩土工程研究人员的众多应用可知[33-35],它是一种研究采场充填体应力分布和揭露稳定性的有效工具。
为了验证本文提出的非胶结充填体、揭露后胶结充填体的三维拱应力解析模型与方法的可靠性,利用FLAC3D分别构建了与解析模型(图1,2)相对应的数值计算模型,并将采场充填体中竖向σv、水平σh正应力随埋深h变化关系的数值解和解析解进行综合对比验证。
FLAC3D数值模型与解析模型选定的采场尺寸相等,均为长L×宽B×高H=10 m×6 m×40 m,采场倾角为90°,按“隔一采一”两步骤阶段空场嗣后充填法的采充顺序进行模拟计算。此处先利用上述示例的采场尺寸和结构进行采场充填体应力解析解和数值解对比,后面再基此综合对比不同采场尺寸(长10~30 m、宽 5~15 m、高 30~60 m)对计算结果的影响。
假设采场围岩为各向同性且服从线弹性模型的结构体,其参数为:容重γr=27 kN/m3、弹性模量Er=40 GPa、泊松比νr=0.2。
假设二步骤采场非胶结充填体是服从摩尔库伦破坏准则的弹塑性结构体,其参数为:容重γu=20 kN/m3、弹性模量Eu=100 MPa、泊松比νu=0.35、黏聚力cu=0、内摩擦角φu=30°、膨胀角ψu=0°。非胶结充填体与上下盘围岩接触面以及与相邻胶结充填体接触面的剪切强度参数为:黏聚力0、内摩擦角δ1u=δ3u=δ13u=r13uφu,δ2u=δ4u=δ24u=r24uφu(取r13u= r24u=0.6)。
假设一步骤采场胶结充填体服从摩尔库伦准则的弹塑性结构体,参数为:容重γc=21 kN/m3、弹性模量Ec=700 MPa、泊松比νc=0.3、黏聚力cc=50 kPa、内摩擦角φc=33°、膨胀角ψc=0°。胶结充填体与上下盘围岩接触面剪切强度参数为:黏聚力c1c=c3c=c13c=λ13ccc(取λ13c=0.5),内摩擦角δ1c=δ3c=δ13c=r13cφc(取r13c=0.8)。
二步骤采场非胶结充填体、一步骤采场胶结充填体及其与采场围岩接触面上接触单元正向(kn)和切向(ks)刚度参数均参照FLAC3D理论手册推荐的滑动分离接触单元模型进行刚度参数计算。关于接触单元刚度参数选取方法及其影响、采场充填层数及开挖步数对充填体应力分布影响及数值模拟方法详见文献[23,25,36]。
图3和4分别展示了二步骤采场非胶结充填体和一步骤采场胶结充填体(揭露后)在三维成拱作用下竖向和水平正应力的三维解析解和三维数值解的对比结果。从图中可看出,虽然解析和数值计算结果存在一定差异性,特别是采场底部竖向应力的数值解略高于解析解,但三维解析法和三维数值法计算得出的充填体正应力整体吻合较好,验证了提出的非胶结充填体、揭露后胶结充填体三维拱应力解析模型与方法的可靠性。
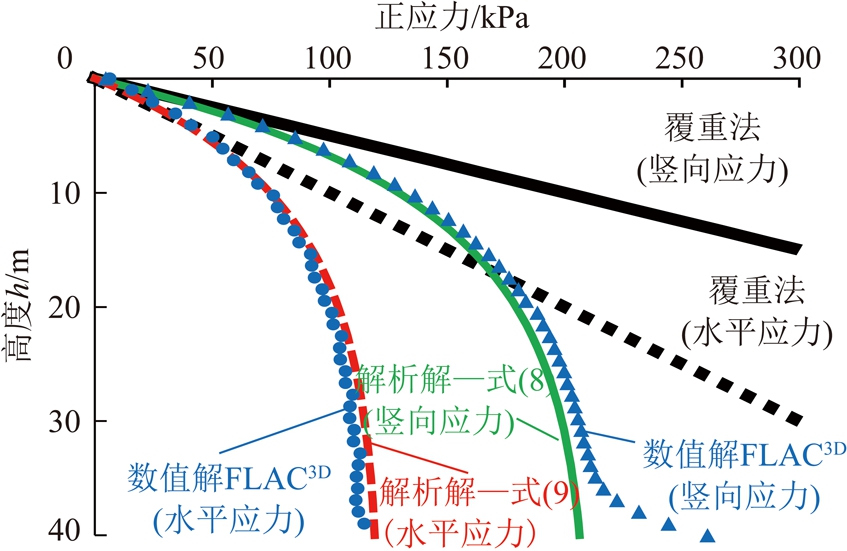
图3 非胶结充填体拱应力解析解和数值解对比
Fig.3 Stress comparison by analytical and numerical methods for uncemented backfill in secondary stope
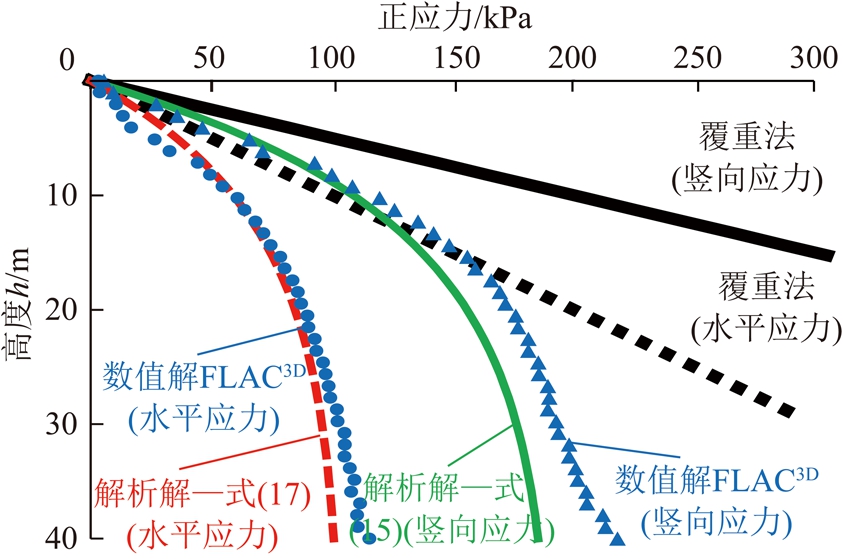
图4 胶结充填体(揭露后)拱应力解析解和数值解对比
Fig.4 Stress comparison by analytical and numerical methods for exposed cemented backfill in primary stope
从图3和4还可看出,充填体同一埋深处,充填体的正应力不同程度的小于覆重法计算的自重应力值,凸显了在研究应用充填体应力分布时考虑应力成拱作用的重要性。而且,在同样采场尺寸条件下,同一埋深处胶结充填体的正应力均小于非胶结充填体的正应力,原因是胶结充填体与围岩接触面黏结力增强了应力成拱作用,胶结充填体自重应力相对更多的转移到采场围岩中。
第1节提出的二步骤采场非胶结充填体和揭露后的一步骤采场胶结充填体的三维拱应力解析模型与方法,一方面揭示了不同类型采场充填体的应力分布模式,另一方面,应力解析方法能为两步骤阶段空场嗣后充填法采充过程中胶结充填体强度需求解析计算提供可靠的力学边界基础。
图5展示了两步骤阶段空场嗣后充填法采充过程中相邻采场充填体分布关系,并给出了一步骤采场胶结充填体的受力图,据此形成了单侧揭露胶结充填体的强度需求三维解析模型。该模型中,假设单侧揭露后的胶结充填体沿底部斜面产生滑动趋势(见物理模型测试和数值模拟的滑动模式研究结果[5,25]),并假设该潜在滑动面与水平面的夹角为α(°)。
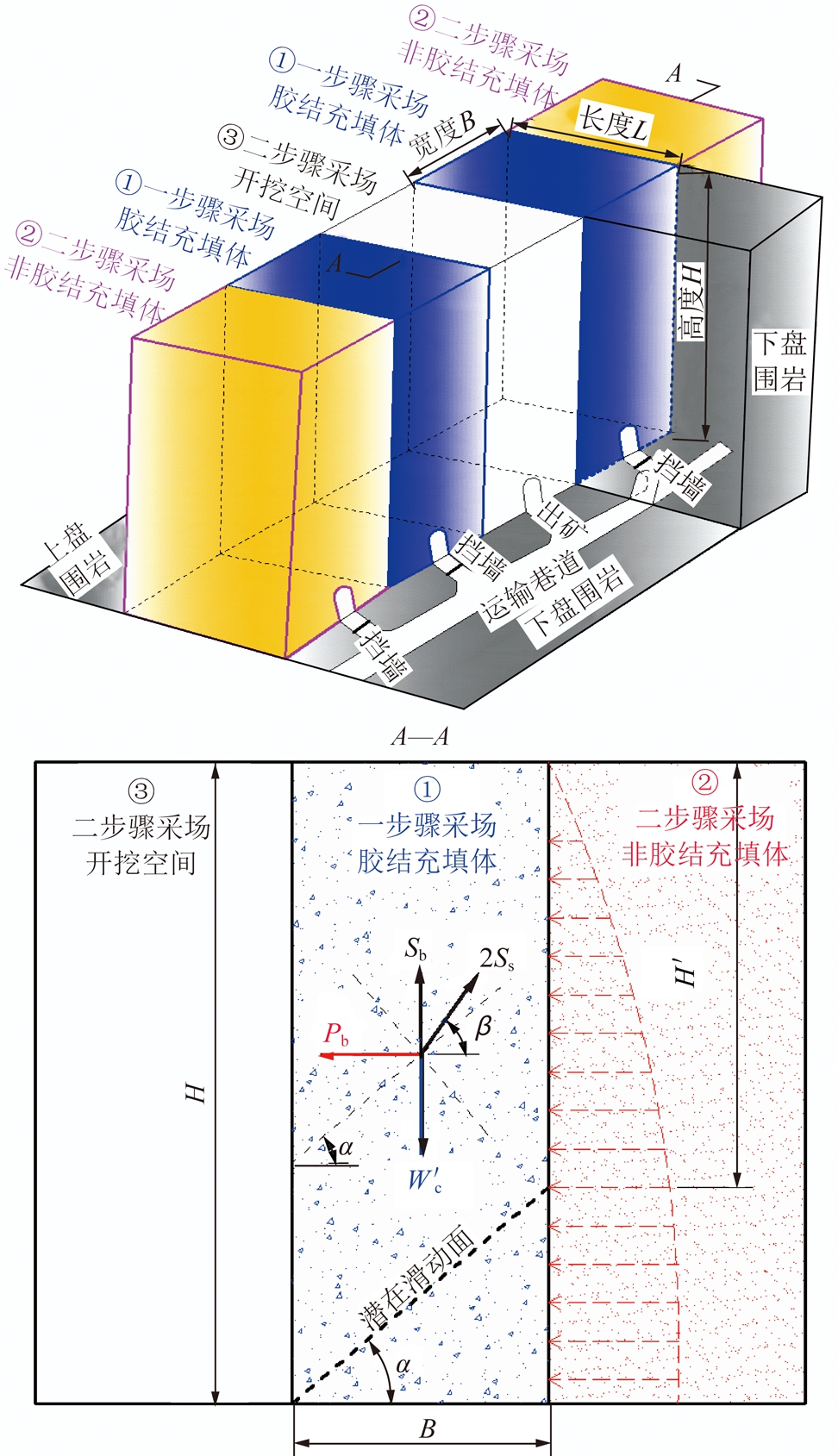
图5 相邻采场采充过程及胶结充填体受力模型
Fig.5 Excavating-filling process of adjacent stopes and the exposed cemented backfill with various acting forces
图5中一步骤采场胶结充填体受力包括:
(1)等效重力![]() 胶结充填体潜在滑动体自重与胶结充填体上表面压力的合力。
胶结充填体潜在滑动体自重与胶结充填体上表面压力的合力。
(18)
式中,H*(=H  (Btan α)/2,m)为潜在滑体等效高度;p0(kPa)为胶结充填体上表面承受压力,可能来自上行设备、充填料浆或顶板压力等。
(Btan α)/2,m)为潜在滑体等效高度;p0(kPa)为胶结充填体上表面承受压力,可能来自上行设备、充填料浆或顶板压力等。
(2)胶结充填体潜在滑动体与上下盘围岩接触面的摩擦力Ss(kN),假设该接触摩擦力与水平面的夹角为任一角度值β( [0,90°])。
[0,90°])。
(19)
式中,H′(=H  Btan α,m)为胶结充填体潜在滑动体后壁上的高度;τhc(kPa)为在埋深h处胶结充填体与上下盘围岩接触面的剪切应力,如图2所示,按式(20)计算。
Btan α,m)为胶结充填体潜在滑动体后壁上的高度;τhc(kPa)为在埋深h处胶结充填体与上下盘围岩接触面的剪切应力,如图2所示,按式(20)计算。
τhc=c13c+σhctan δ13c=
λ13ccc+σhctan(r13cφc)
(20)
式中,σhc(kPa)为三维成拱状态下单侧揭露后的一步骤采场胶结充填体在埋深h处的水平正应力(按式(17)计算)。但根据胶结充填体拱应力的数值模拟结果发现:当胶结充填体的黏聚力(或按比例系数λ13c换算为接触面黏聚力后)超过某一界限值时,充填体的拱应力便失去了对其黏聚力持续增加的敏感性,该胶结充填体黏聚力的界限值在50 kPa左右[23-24]。LI和AUBERTIN[37]得出类似倾斜采场充填体黏聚力界限值约30 kPa。
根据胶结充填体拱应力分布数值计算结果,在式(17)基础上,选定胶结充填体黏聚力的界限值为ccon=50 kPa,当胶结充填体黏聚力值大于该界限值(50 kPa)时,胶结充填体水平应力σhc不再随黏聚力的增加而降低。此时胶结充填体水平拱应力σhc按式(21)计算。
![]()
(21)
将式(20)和(21)代入式(19)积分计算,得成拱作用下单侧揭露后胶结充填体与上下盘围岩接触面的摩擦力Ss,如式(22)所示。
Ss=BH*λ13ccc+X
(22)
![]()
(23)
η=γcLB-2Bccon
(24)
ξ=2Btan δ13c+Ltan δ4c
(25)
式中,X,η,ξ均为中间变量。
(3)二步骤采场非胶结充填体通过接触作用,向相邻胶结充填体施加侧向推力Pb(kN)和竖向摩擦力Sb(kN),影响单侧揭露胶结充填体的稳定性,进而影响胶结充填体的强度需求。二步骤采场非胶结充填体对相邻胶结充填体的侧向推力和竖向摩擦力分别按式(26),(27)计算。
Pb=![]() σhuLdh
σhuLdh
(26)
Sb=![]() τhuLdh=
τhuLdh=![]() [σhutan(r24uφu)]Ldh
[σhutan(r24uφu)]Ldh
(27)
式中,σhu(kPa)为三维成拱作用的二步骤采场非胶结充填体在埋深h处的水平正应力,如图1所示,按式(9)计算。将式(9)代入式(26),(27)进行求解:
![]()
(28)
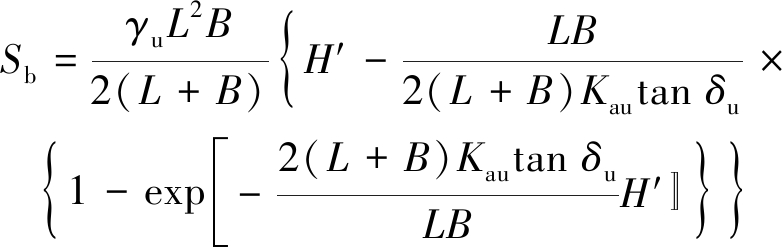
(29)
结合二步骤采场非胶结充填体与揭露后的一步骤采场胶结充填体三维拱应力解析方法,推导了图5中作用于胶结充填体潜在滑动体的各力学边界计算方法,将各力学边界在沿着和垂直于潜在滑动面方向进行因式分解,可基于极限平衡法得出胶结充填体潜在滑动体的安全系数FS。
但是,图5中的2个方向角仍然无法确定,即α(潜在滑动面与水平面夹角)和β(胶结充填体和上下盘围岩接触面摩擦力Ss与水平面夹角)。在原始Mitchell模型[5]及其修正模型中[7-10],均选用了α =45°+φc/2,这主要基于胶结充填体处于主动压力状态的假设,该假设通过单侧揭露胶结充填体的物理模型测试[5]和数值模拟[25,34]获得验证。此外,充填体与上下盘围岩接触面的摩擦力方向以往大多假设是竖直向上的(β =90°),而近期LI和AUBERTIN[11]通过单侧揭露充填体稳定性的模拟分析,认为胶结充填体揭露后的滑动趋势可分两部分:上部矩形充填体β =90°,下部分三角滑动体β ≈ 45°+φc/2。
值得注意的是,以往研究中关于α和β的取值都基于单个孤立的胶结充填体强度需求计算模型,而本文考虑了实际采充过程中相邻采场充填体的力学作用关系后(例如非胶结充填体对胶结充填体的侧向推力Pb),可能导致α,β存在不同程度取值变化的可能性,使α,β与以往Mitchell法及后期修正法[5,7-11]的取值有所不同。
对此,根据α,β可能的取值情况,本文具体构建了4种解析模型,分别推导了相应胶结充填体的安全系数FS和强度需求的计算方法,后面再与FLAC3D数值模拟的强度需求结果进行对比验证,从中优选出最合理的解析模型。
(1)α =45°+φc/2,β =90°
首先沿用Mitchell模型及后期修正模型[5,7-11]的角度取值假设(即α =45°+φc/2,β =90°),而胶结充填体的力学边界按图5中力学模型选取。
沿潜在滑动面的抗滑力为胶结充填体黏聚力cc与滑动面面积的乘积,再加上垂直于滑动面的压力与内摩擦系数的乘积。沿潜在滑动面的下滑力为图5中各作用力沿滑动面的分量。因式分解后,得出单侧揭露胶结充填体安全系数FS为
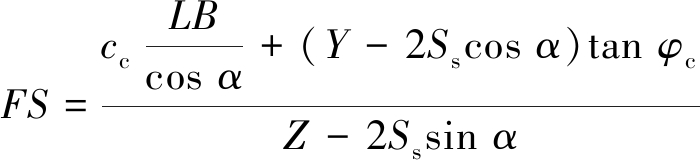
(30)
式中,Y和Z为中间变量,分别按式(31)和式(32)计算。
(31)
![]()
(32)
将式(22)代入式(30)后进行公式变换,可得胶结充填体强度需求(黏聚力cc)计算方法:
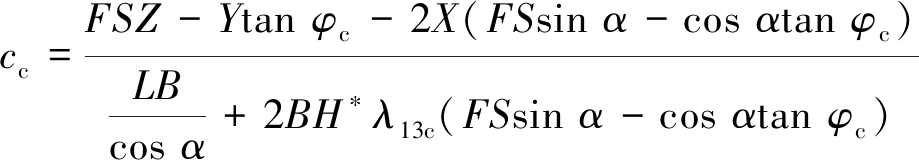
(33)
式中,λ13c(=c13c/cc; [0,1])为一步骤采场胶结充填体与上下盘围岩接触面(图2中面F1c和面F3c)的黏聚力c13c与胶结充填体黏聚力cc的比值;X为中间变量,按式(23)计算。
[0,1])为一步骤采场胶结充填体与上下盘围岩接触面(图2中面F1c和面F3c)的黏聚力c13c与胶结充填体黏聚力cc的比值;X为中间变量,按式(23)计算。
(2)α =β =45°+φc/2
此模型中,假设各力学边界对一步骤采场胶结充填体潜在滑动体的滑动面方向角α不产生影响,仍沿用Mitchell模型及其后期修正模型[5,7-11]的角度取值。但本文考虑的各力学边界可能迫使胶结充填体沿滑动面的整体滑移,使胶结充填体与上下盘围岩接触面摩擦力的等效方向与整体滑移方向平行,即β =45°+φc/2。此时单侧揭露胶结充填体的安全系数FS为
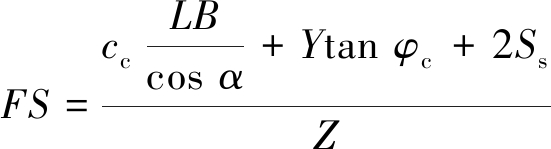
(34)
将式(22)代入式(34)后进行公式变换,可得胶结充填体强度需求(黏聚力cc)计算方法:
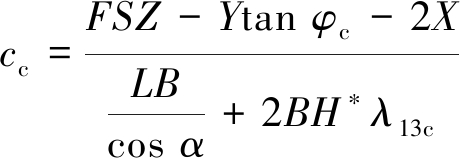
(35)
(3)0°≤α =β≤90°
此模型中,假设一步骤采场胶结充填体沿底部滑动面产生了整体滑移趋势,胶结充填体与上下盘围岩接触面的摩擦力方向与潜在滑移方向平行,即α =β。但是,由于三维成拱作用下各力学边界的影响,导致方向角α(=β)有可能是[0,90]范围内的任一角度值,而不是Mitchell模型中[5]假设的α =45°+φc/2。
假设α(=β)为[0,90]范围内的任意值,即0°≤α =β≤90°,通过考虑图5中单侧揭露胶结充填体潜在滑动体的静力平衡状态,可得出与式(34)相同的公式计算滑动体的安全系数FS,且胶结充填体强度需求(黏聚力cc)的计算方法与式(35)相同。但与模型(2)不同的是:式(34)和式(35)中代入的方向角α(=β)可能为任意值。
为获取该任意方向角的取值α(=β),将单侧揭露胶结充填体潜在滑动体的安全系数FS假设为变量α的函数,通过对函数FS(α)求导求极值的方法,获取方向角度α在[0,90]范围的极值。其物理意义是:在该滑动角度极值条件下,侧向揭露胶结充填体的安全系数FS取最小值时,对应的充填体强度需求值cc是在保证极限安全条件下的强度需求最小值。
将式(34)假设为安全系数FS对方向角α的函数FS(α),对变量α求导,如式(36)所示。
![]()
(36)
![]()
(37)
![]()
(38)
![]()
(39)
![]()
(40)
利用函数导数求极值的数学方法,设定式(36)导数为∂FS/∂α=0,其他所有参数可按实际情况取值(如胶结充填体容重、采场长宽高等)。建议借助Microsoft Excel®计算,可快捷计算出不同取值条件下方向角α(=β)的极值。进而将该方向角极值代入式(35),可得不同参数条件下胶结充填体强度需求值(黏聚力cc)。
考虑到实际工程应用中极限平衡模型安全系数的选取方法,可在求解方向角α极值时选定FS=1.0为最危险状态(保证极限安全条件),而不必追求比1.0更低的安全系数值,因为安全系数取低于1.0的不同值在实际工程应用中都说明充填体已破坏,不具有实际工程意义。
(4)α =45°+φc/2,0°≤β≤90°(推荐)
此模型中,假设作用于胶结充填体的各力学边界对潜在滑动体的滑动面方向角α不产生影响,仍沿用Mitchell模型取值(α =45°+φc/2),但胶结充填体与上下盘围岩接触面摩擦力Ss的方向角β可能在[0,90]范围取任一值(0°≤β≤90°),此时单侧揭露胶结充填体安全系数FS为
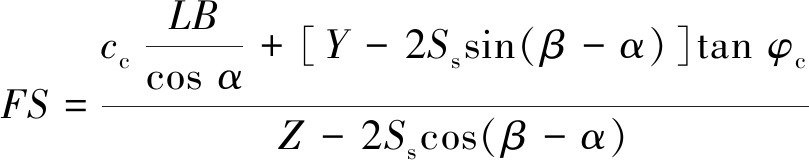
(41)
为获取胶结充填体与上下盘围岩接触面摩擦力Ss等效方向角β的取值,同样将胶结充填体的安全系数FS假设为该等效方向角的函数FS(β),同样利用求导求极值的数学方法,计算变量β的极值,使目标函数FS取得最小值,获取在保证极限安全条件下的充填体最小强度需求值。
将式(41)对变量β求导,设定导数∂FS/∂β=0,并结合sin2(β-α)+cos2(β-α)=1,可得变量β极值的计算方法,如式(42)所示。
(42)
式中,U为中间变量,可按式(43)计算。
(43)
利用Microsoft Excel®计算,代入其他相关参数(如胶结充填体容重、长宽高等),搜索计算了不同工况参数条件下的极值β。同样地,考虑到实际工程应用中极限平衡法安全系数的选取方法,在求β极值时选定FS=1.0作为最危险状态(极限平衡状态)。
经不同采场尺寸和充填体力学参数等条件下迭代计算,得出β极值总趋近于式(44)结果。
β=45°-φc/2
(44)
导致该结果的原因是:对于一步骤采场胶结充填体和相邻二步骤采场非胶结充填体的复合共同体,一步骤采场胶结充填体发挥了类似于挡土墙的功能作用,非胶结充填体的侧向推力导致单侧揭露胶结充填体处于被动土压力状态(与摩尔圆中取Rankine被动土压力时的方向角相似)。
式(44)结合α =45°+φc/2后,得α  β =φc,将其代入式(41)并进行公式变换,可得式(45)用于极限平衡状态下(FS=1.0时)单侧揭露胶结充填体的强度需求(黏聚力cc)计算。
β =φc,将其代入式(41)并进行公式变换,可得式(45)用于极限平衡状态下(FS=1.0时)单侧揭露胶结充填体的强度需求(黏聚力cc)计算。
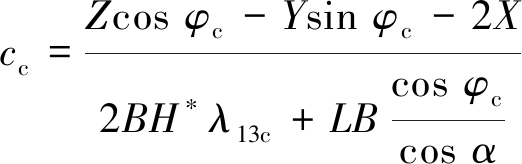
(45)
为验证实际采充过程中(图5),考虑采场充填体三维拱应力后,单侧竖向揭露胶结充填体强度需求解析模型的可靠性,并从4种解析方法中优选出最合理的强度需求解析模型,利用FLAC3D构建了图5所示的解析模型相对应的数值计算模型,按表1的计算方案,数值搜索计算了不同采场尺寸、不同充填体力学参数条件下强度需求数值解,再与同等参数条件下4种解析模型计算的强度需求解析解进行综合对比验证。
表1 胶结充填体强度需求数值解计算方案
Table 1 Comparison program of numerical simulations for the strength requirement of cemented backfill
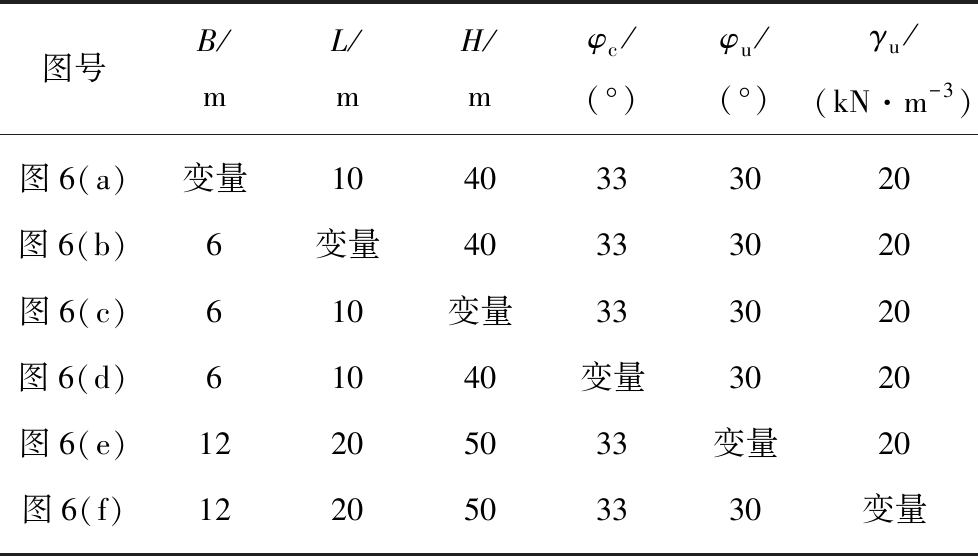
图号B/mL/ mH/ mφc/(°)φu/(°)γu/(kN·m-3)图6(a)变量1040333020图6(b)6变量40333020图6(c)610变量333020图6(d)61040变量3020图6(e)12205033变量20图6(f)1220503330变量
表1展示了胶结充填体强度需求数值解计算方案,除了重点研究参数外,按控制变量法原则将其他参数固定:胶结充填体容重γc=21 kN/m3、弹性模量Ec=700 MPa、泊松比νc=0.3、膨胀角ψc=0°、胶结充填体黏聚力界限值ccon=50 kPa、胶结充填体与上下盘围岩接触面黏聚力与胶结充填体黏聚力的比例系数λ13c=0.5、胶结充填体与上下盘围岩接触面内摩擦角与胶结充填体内摩擦角的比例系数r13c=0.8;非胶结充填体的弹性模量Eu=100 MPa、泊松比νu=0.35、黏聚力cu=0、膨胀角ψu=0°、非胶结充填体与上下盘围岩接触面以及与相邻胶结充填体接触面的内摩擦角与非胶结充填体内摩擦角的比例r13u= r24u=0.6。
将采用控制变量法计算得出的不同条件下FLAC3D数值解和4种解析解的胶结充填体强度需求计算结果进行对比验证,结果如图6所示。从图6可看出,不同采场尺寸(长L=10~30 m、宽B=5~15 m、高H=30~60 m)、胶结充填体力学参数(内摩擦角φc=24°~42°)、非胶结充填体力学参数(内摩擦角φu=20°~35°、容重γu=17~23 kN/m3)条件下,解析模型4(式(45))计算的极限平衡状态下(FS=1.0)胶结充填体强度需求值与FLAC3D数值模拟得出的强度需求值吻合度最好。因此,推荐解析模型4及式(45)作为考虑采场充填体三维拱应力后单侧揭露胶结充填体强度需求的最优解析计算模型与方法。
本文推导的胶结充填体强度需求解析方法及开展数值计算时,均假设充填体服从摩尔库伦破坏准则,得出的强度需求结果采用了胶结充填体黏聚力cc进行表征(式(45)和图6)。而在工程实际中,常采用单轴抗压强度(相对简单易测)表征充填体的强度需求。假设胶结充填体黏聚力cc与其单轴抗压强度σc的比值为M(=cc/σc)。不同类型的胶结充填体,该比例系数不尽相同,它受充填骨料级配、胶凝材料类型、配比参数等因素影响。根据直线型摩尔库伦强度曲线,可利用σc=(2cccos φc)/(1-sin φc)进行M值计算。Mitchell解析模型[5]假设胶结充填体内摩擦为0,进而得出M=0.5。ASKEW等[38]通过澳大利亚某铅锌矿尾砂胶结充填体和河沙胶结充填体的强度测试,认为该矿胶结充填体M=0.35。ARIOGLU[39]根据土耳其某钨矿废石胶结充填体的强度测试,认为该矿废石胶结充填体M=0.18。本文建议利用实际矿山胶结充填体的实验测试获取相应换算系数M值,也可参考以往的试验结果选取。
图6中4种充填体强度需求(黏聚力)解析模型和数值模拟结果比较时,虽然模型4结果与数值模拟最接近,但仍然存在一定误差,其主要原因为:① 为构建基于极限平衡法的充填体强度需求解析模型,将侧向揭露采场胶结充填体的潜在滑动面假设为一个平直面(图5),其面积与胶结充填体黏聚力的乘积是抗滑力的主要组成部分,但在数值模拟结果中,该潜在滑面并不是完美平直面,而近似于一个圆弧面的滑动带[25],导致数值模型中抗滑面积大于解析模型中的抗滑面积,进而导致同等条件下数值计算的充填体强度需求小于解析计算结果;② 基于极限平衡法的解析模型中,无法考虑胶结充填体的内部变形,等效于将滑动体单元假设为刚体,其后壁受侧向推力时将产生瞬时下滑趋势,而数值模型中充填体假设为弹塑性体,其后壁受侧向推力时将基于泊松效应产生内部变形,相当于抵消了侧向推力引起的部分下滑力,进而导致同等条件下数值计算的充填体强度需求小于解析计算结果。
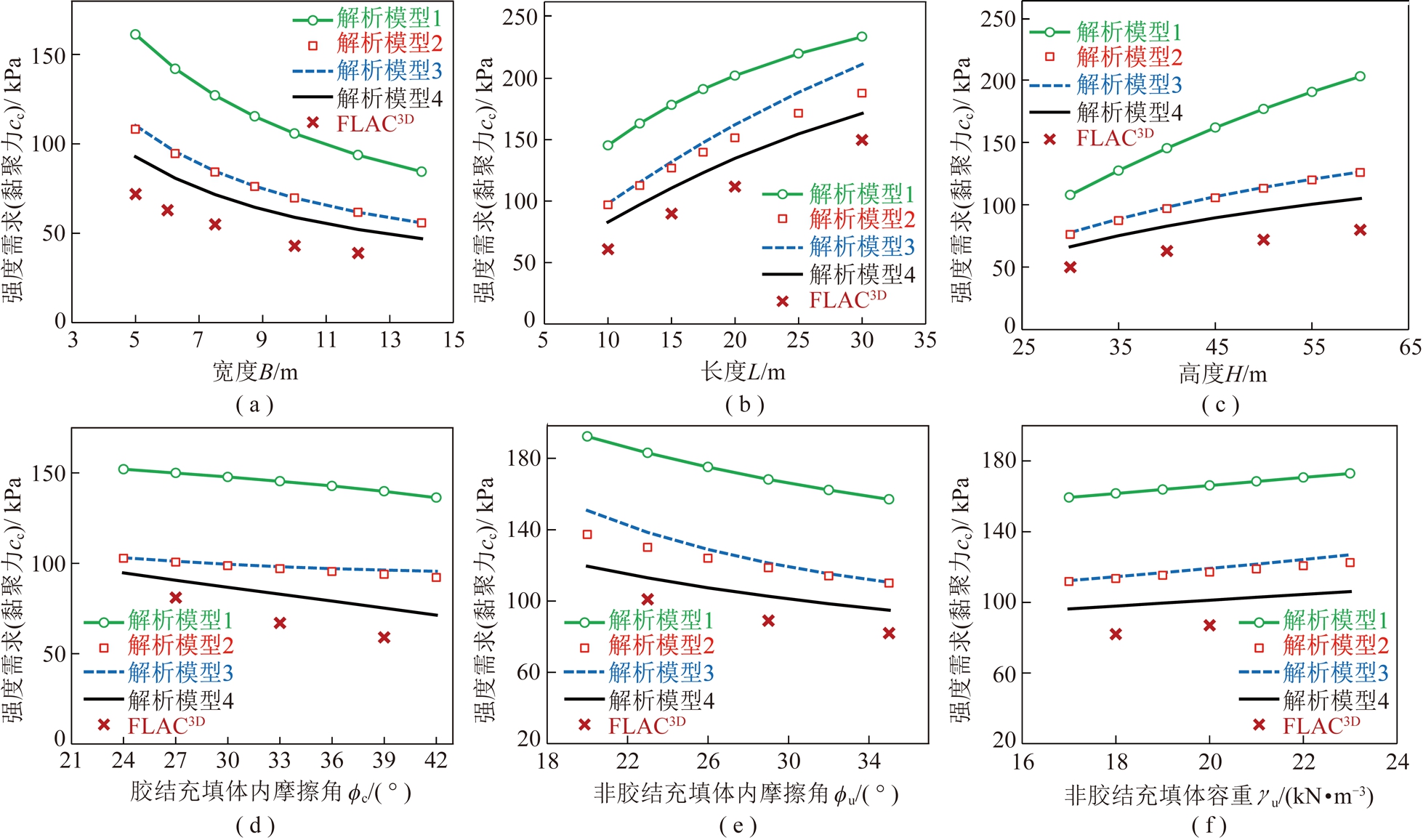
图6 数值模型和4种解析模型计算的极限平衡状态下一步骤采场胶结充填体强度需求(黏聚力cc)对比
Fig.6 Strength requirement comparison of the cemented backfill under limit equilibrium state with FLAC3D simulations and four analytical models
本文提出的采场充填体应力解析模型是基于理论力学的静力平衡法构建的,模型中重点考虑了充填体的、充填体-围岩接触面的抗剪强度参数对充填体应力分布的影响,而没有考虑围岩的力学性质对充填体应力分布的影响,这主要基于以下假设条件:① 金属矿山矿岩强度、刚度通常是充填体相应参数的十几倍至上百倍,充填体相对围岩是十分软弱的,两者应力值通常不在同一数量等级,因而借鉴土力学领域类似工况的应力成拱理论,构建了采场充填体应力解析模型;② 采场矿岩在爆破、出矿等回采工序完成后,通常需要一定时间才能完成采场空区充填,且需一定养护龄期才具备强度,在此期间,围岩储存大部分能量已释放,因此围岩力学性质对充填体应力分布影响不是本文考虑的关键因素,充填体应力更主要受其自重及其与围岩接触摩擦作用影响。
本文得出的解析和数值计算模型及其方法均基于一定假设条件,包括:假设采场充填体是均匀的各向同性的且服从摩尔库伦破坏准则的弹塑性材料;假设强度需求计算时单侧揭露的胶结充填体是处于极限平衡状态(等效于安全系数FS=1.0);假设采场边界为平直的、倾角为90°,且不考虑实际采场充填体参数不均匀分布等复杂现场条件等。而在实际地下采场中,胶结充填体由于沉降、固结、离析、分层等复杂成形过程,导致达到完全均匀的各向同性的物理力学性质是困难的[40]。因此,在实际应用中,需要以本文解析模型计算的胶结充填体强度需求理论解为基础,考虑不同矿山不同时期的充填技术水平和采场充填质量控制效果,选取与矿山整体充填技术水平相匹配的浮动安全系数,浮动安全系数选取方法可参考以往论文[36],最终获取满足实际矿山不同时期不同工况条件的胶结充填体强度需求。此外,在后续研究中将以本文模型为基础,探索采场倾角、采场结构、充填体不均匀分布特征、深部围岩高应力和大变形力学性质等因素对采场充填体应力和强度需求的影响。
(1)借鉴土力学应力拱理论,结合两步骤阶段空场嗣后充填采矿法的采充过程,分析了相邻采场充填体及其与上下盘围岩的接触关系,分别构建了二步骤采场非胶结充填体、一步骤采场胶结充填体的三维拱应力解析模型,推导得出了不同采场充填体竖向、水平应力的解析方法。
(2)利用FLAC3D构建了与充填体应力解析模型相对应的数值模型,计算了充填体竖向、水平应力的分布模式,对比得出了三维解析法和数值模拟法得出的充填体应力具有良好的吻合度,验证了提出的非胶结充填体、揭露后胶结充填体三维拱应力解析计算模型及方法的可靠性。
(3)构建了一步骤采场单侧揭露胶结充填体强度需求解析模型,结合非胶结充填体和胶结充填体的三维拱应力解析方法,获取了模型中作用于胶结充填体的各向力学边界,并基于胶结充填体滑动面方向角、潜在滑体与上下盘围岩接触面摩擦力方向角的不同取值情况,提出了4种单侧揭露胶结充填体安全系数和强度需求的解析计算模型与方法。
(4)利用FLAC3D构建了与胶结充填体强度需求解析模型相对应的数值模型,开展了不同采场尺寸(长、宽、高)、不同胶结和非胶结充填体力学参数(内摩擦角、容重)条件下的强度需求三维数值解的搜索计算,并与4种解析方法计算的强度需求结果进行了对比分析,得出了当胶结充填体底部滑面方向角α =45°+φc/2且潜在滑体与上下盘围岩接触面摩擦力方向角β=45°-φc/2时,胶结充填体强度需求的三维解析解和数值解吻合度最好,最终推荐了解析模型4及式(45)作为阶段空场嗣后充填采矿法中胶结充填体强度需求理论解的最优解析模型与方法。
[1] DARLING P.SME mining engineering handbook (Third edition)[M].Denver:Society for Mining,Metallurgy,and Exploration,Colorado,USA,2011.
[2] HASSANI F,ARCHIBALD J.Mine backfill[M].Montreal:Canadian Institute of Mine,Metallurgy and Petroleum,1998.
[3] BELEM T,MBONIMPA M.Minimum strength required for resisting to cyclic softening/failure of cemented paste backfill at early age[A].Proceedings of the 3rd International Symposium on Mine Safety Science and Engineering[C].Montreal,2016.
[4] 吴爱祥,沈慧明,姜立春,等.窄长型充填体的拱架效应及其对目标强度的影响[J].中国有色金属学报,2016,26(3):648-653.
WU Aixiang,SHEN Huiming,JIANG Lichun,et al.Arching effect of long-narrow cemented paste backfill body and its effect on target strength[J].Chinese Journal of Nonferrous Metals,2016,26(3):648-653.
[5] MITCHELL R J,OLSEN R S,SMITH J D.Model studies on cemented tailings used in mine backfill[J].Canadian Geotechnical Journal,1982,19(1):14-28.
[6] DUNCAN J M,WRIGHT S G.Soil strength and slope stability[M].Hoboken:John Wiley & Sons,2005.
[7] DIRIGE A P E,MCNEARNY R L,THOMPSON D S.The effect of stope inclination and wall rock roughness on back-fill free face stability[A].Rock Engineering in Difficult Conditions,Proceedings of the 3rd Canada-US Rock Mechanics Symposium,DIEDERICHS M and GRASSELLI G (Eds.)[C].Toronto,2009,4152.
[8] ZOU S,NADARAJAH N.Optimizing backfill design for ground support and cost saving[A].Golden Rocks 2006,the 41st US Symposium on Rock Mechanics (USRMS),American Rock Mechanics Association[C].Golden:2006:7-21.
[9] LI L.Generalized solution for mining backfill design[J].International Journal of Geomechanics,2014,14(3):04014006.
[10] LI L.Analytical solution for determining the required strength of a side-exposed mine backfill containing a plug[J].Canadian Geotechnical Journal,2014,51(5):508-519.
[11] LI L,AUBETIN M.An improved method to assess the required strength of cemented backfill in underground stopes with an open face[J].International Journal of Mining Science and Technology,2014,24(4):549-558.
[12] LIU G S,LI L,YANG X C,et al.Required strength estimation of a cemented backfill with the front wall exposed and back wall pressured[J].International Journal of Mining and Mineral Engineering,2018,9(1):1-20.
[13] 曾照凯,张义平,王永明.高阶段采场充填体强度及稳定性研究[J].金属矿山,2010,(1):31-34.
ZENG Zhaokai,ZHANG Yiping,WANG Yongming.Research on the strength and stability on fill body of high-bench stope[J].Metal Mine,2010,(1):31-34.
[14] 朱志彬,刘成平.充填体强度计算及稳定性分析[J].采矿技术,2008,8(3):15-17,25.
ZHU Zhibin,LIU Chengping.Strength calculation and stability analysis of backfill[J].Mining Technology,2008,8(3):15-17,25.
[15] 刘志祥,李夕兵,戴塔根,等.尾砂胶结充填体损伤模型及与岩体的匹配分析[J].岩土力学,2006,27(9):1442-1446.
LIU Zhixiang,LI Xibing,DAI Tagen,et al.On damage model of cemented tailings backfill and its match with rock mass[J].Rock and Soil Mechanics,2006,27(9):1442-1446.
[16] 刘志祥,李夕兵,赵国彦,等.充填体与岩体三维能量耗损规律及合理匹配[J].岩石力学与工程学报,2010,29(2):344-348.
LIU Zhixiang,LI Xibing,ZHAO Guoyan,et al.Three dimensional energy dissipation laws and reasonable matches between backfill and rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):344-348.
[17] LIU Z X,LAN M,XIAO S Y,et al.Damage failure of cemented backfill and its reasonable match with rock mass[J].Transactions of Nonferrous Metals Society of China,2015,25(3):954-959.
[18] 刘志祥,李夕兵,张义平.基于混沌优化的高阶段充填体可靠性分析[J].岩土工程学报,2006,28(3):348-352.
LIU Zhixiang,LI Xibing,ZHANG Yiping.Reliability analysis of high level backfill based on chaotic optimization[J].Chinese Journal of Geotechnical Engineering,2006,28(3):348-352.
[19] 刘志祥,刘青灵,周士霖.基于可靠度理论的充填体强度设计[J].矿冶工程,2012,32(6):1-4,8.
LIU Zhixiang,LIU Qingling,ZHOU Shilin.Backfill strength design based on reliability theory[J].Mining and Metallurgical Engineering,2012,32(6):1-4,8.
[20] MARSTON A.The theory of external loads on closed conduits in the light of latest experiments[A].Proceedings of the Ninth Annual Meeting of the Highway Research Board[C].Washington,D.C.:1930,9:138-170.
[21] THOMPSON B,BAWDEN W,GRABINSKY M.In situ measurements of cemented paste backfill at the Cayeli Mine[J].Canadian Geotechnical Journal,2012,49(7):755-772.
[22] EIMKADMI N,AUBERTIN M,LI L.Effect of drainage and sequential filling on the behavior of backfill in mine stopes[J].Canadian Geotechnical Journal,2014,51(1):1-15.
[23] LIU G S,LI L,YANG X C,et al.Numerical analysis of stress distribution in backfilled stopes considering interfaces between the backfill and rock walls[J].International Journal of Geomechanics,2017,17(2):06016014.
[24] LIU G S,LI L,YANG X C,et al.A numerical analysis of the stress distribution in backfilled stopes considering nonplanar interfaces between the backfill and rock walls[J].International Journal of Geotechnical Engineering,2016,10(3):271-282.
[25] LIU G S,LI L,YANG X C,et al.Stability analyses of vertically exposed cemented backfill:A revisit to Mitchell’s physical model tests[J].International Journal of Mining Science and Technology,2016,26(6):1135-1144.
[26] 刘钦,李地元,刘志祥,等.水平推力作用下抗滑桩间土拱效应影响因素的数值分析[J].中南大学学报(自然科学版),2011,42(7):2071-2077.
LIU Qin,LI Diyuan,LIU Zhixiang,et al.Numerical analysis of influence factors on soil arching effect between anti-sliding piles under horizontal pushing loads[J].Journal of Central South University (Science Edition),2011,42(7):2071-2077.
[27] 涂兵雄,贾金青.考虑土拱效应的黏性填土挡土墙主动土压力研究[J].岩石力学与工程学报,2012,31(5):1064-1070.
TU Bingxiong,JIA Jinqing.Research on active earth pressure behind rigid retaining wall from clayey backfill considering soil arching effects[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(5):1064-1070.
[28] LI L,AUBERTIN J D,DUBE J S.Stress distribution in a cohesionless backfill poured in a silo[J].Open Civil Engineering Journal,2014,8(1):1-8.
[29] GRABINSKY M W,BAWDEN W F.In situ measurements for geomechanical design of cemented paste backfill systems[A].Proceeding of 9th International Symposium in Mining with Backfill[C].Montreal,2007.
[30] LI L,AUBERTIN M,BELEM T.Formulation of a three dimensional analytical solution to evaluate stresses in backfilled vertical narrow openings[J].Canadian Geotechnical Journal,2005,42(6):1705-1717.
[31] PIRAPAKARAN K,SIVAKUGAN N.Arching within hydraulic fill stopes[J].Geotechnical and Geological Engineering,2007,25(1):25-35.
[32] SOBHI M A,LI L,AUBERTIN M.Numerical investigation of earth pressure coefficient along central line of backfilled stopes[J].Canadian Geotechnical Journal,2017,54(1):138-145.
[33] VEESTRA R.A design procedure for determining the in situ stresses of early age cemented paste backfill[D].Toronto:University of Toronto,Canada,2013.
[34] FALAKNAZ N.Analysis of geomechanical behavior of two adjacent backfilled stopes based on two and three dimensional numerical simulations[D].Montréal:Polytechnique Montreal,Canada,2014.
[35] EMAD M Z.Dynamic performance of cemented rockfill under blast-induced vibrations[D].Montréal:McGill University,2013.
[36] 刘光生.充填体与围岩接触成拱作用机理及强度模型研究[D].北京:北京科技大学,2017.
LIU Guangsheng.Required strength model of cemented backfill with research on arching mechanism considering backfill-rock interaction[D].Beijing:University of Science and Technology Beijing,2017.
[37] LI L,AUBERTIN M.Numerical investigation of the stress state in inclined backfilled Stopes[J].International Journal of Geomechanics,2009,9(2):52-62.
[38] ASKEW J E,MCCARTHY P L,FITZGERALD D J.Backfill research for pillar extraction at ZC/NBHC[A].Mining with Backfill[C].Sudbury:1978:100-110.
[39] ARIOGLU E.Design aspects of cemented aggregate fill mixes for tungsten stoping operations[J].Mining Science and Technology,1984,1(3):209-214.
[40] LIU G S,LI L,YAO M,et al.An investigation of the uniaxial compressive strength of a cemented hydraulic backfill made of alluvial sand[J].Minerals,2017,7(1):4.