煤矿地下水库是从水资源保护角度来描述的一种提高矿井水利用率的建设模式,它是通过构筑人工坝体将不连续的煤柱坝体连接起来,形成地下水库坝体,利用采空区垮落岩体间的自由空隙来进行储水,将矿井水注入采空区内,进行沉淀、过滤、吸附,然后作为矿区生产生活水源,实现矿井水的自然储存和净化[1]。
储水能力是评价所修建煤矿地下水库是否成功的重要指标,储水能力的强弱与水库库容大小有着直接的关联,影响煤矿地下水库储水能力的因素众多,包括工作面尺寸、开采方法、煤层顶底板岩层岩性等,亦即影响水库库容大小,库容确定是建设煤矿地下水库的核心组成部分。储水系数作为表征煤矿地下水库储水能力的主要因素受到众多学者的关注,等同于空隙度。顾大钊[2]指出储水系数取决于岩体空隙度,随时间动态变化,受覆岩结构、开采参数、矿山压力和岩体块度等多种因素影响;陈苏社[3]认为煤矿地下水库的储水空间是由垮落带和裂隙带构成,相应的储水系数等于垮落带孔隙率或裂隙带孔隙率;李全生等[4]给出了储水系数与采空区破碎岩体碎胀系数二者间的数学关系式;除此之外,可以利用大型三维震动模拟试验台对其进行物理模拟研究,结合矿区抽排水工程试验得到储水系数的具体数值。在实际工程应用中,储水系数的数值大部分来源于经验值范围或矿区抽排水工程试验(10%~35%),虽然目前针对煤矿地下水库的研究有很多,但是少有学者给出储水系数的具体计算公式,无法实现对各个煤矿地下水库储水系数的具体数值进行精确计算与合理分析。
笔者结合前述学者的研究内容与成果,以宽沟煤矿地下水库为例,结合Terzaghi有效应力原理,依据储水系数的基本定义推导得到具体计算公式,综合考虑包括地层埋深、地层条件、顶板垮落状况、松散体密度等影响储水系数的众多因素,并对各因素进行理论分析,以此求解宽沟煤矿地下水库储水系数的数值,提出煤矿地下水库储水系数的最佳计算方法,为煤矿地下水库储水能力的评估与库容的确定建立科学的根据。
1 研究背景
宽沟煤矿由神华新疆公司和天山电力公司共同投资开发建设,工程计划总投资5.26亿元,年产500万t,矿区位于呼图壁县雀尔沟镇宽沟13号井田境内,如图1所示,是新疆目前煤炭资源储量最大的矿区,经初步勘探查明,矿区地质储量达10亿t以上。该矿于2004-08-25开工建设,2007年9月投入试生产。
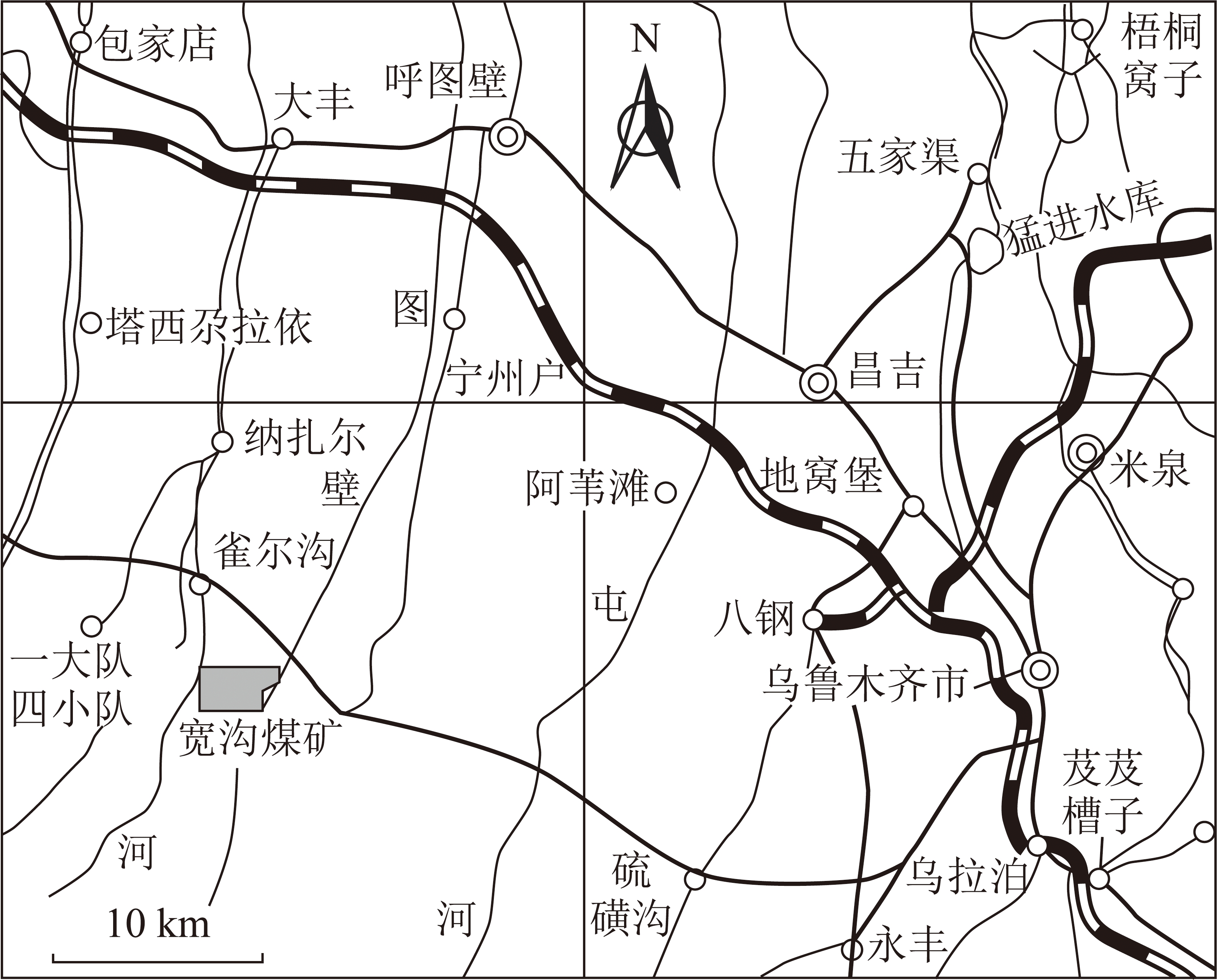
图1 宽沟煤矿地理位置示意
Fig.1 Geographical location of Kuangou Coal Mine
2015年3月,开展宽沟煤矿地下水库建设的前期准备工作,包括详细了解宽沟煤矿矿区地层、矿区构造、矿井水文地质特征、矿井涌水量、矿井水质等情况。经地质勘探,矿区地层主要由侏罗系砂岩、砾岩及煤系地层组成。根据勘查区水文地质条件,矿区主要充水水源有碎屑岩类孔隙裂隙水、采空区积水,其次为地表水和大气降水,矿井涌水量逐年递增。
综合考虑各方面指标,宽沟煤矿反斜井开拓、同煤层上行开采的开采方式有利于建设地下水库,在两煤层错开区域建设地下水库,规避下区段工作面顶空、顶水作业的危险性,提高了工作面的安全性。同年9月,地下水库工程正式施工,开展水库、坝体及附近构筑物等稳定性监测、数据反馈分析。2016年12月宽沟煤矿地下水库建成,并投入正式运行,达到了地下污水不出井,矿井水利用率提高到了60%以上,形成了适用于缓倾斜煤系地层的矿井水净化利用与协调开采技术设计方法和配套技术标准。
2 储水系数数学模型的建立
在进行宽沟煤矿地下水库储水系数的计算时,可以首先确定该煤矿地下水库所在煤层上覆岩层垮落前的示意图如图2所示,便于读者了解实际计算背景。需要指出的是,由于倾斜煤层也具备建造煤矿地下水库的条件,在建立储水系数数学模型时考虑其影响。

图2 煤层上覆岩层冒落前示意
Fig.2 Before the overlying strata falling in the coal seam
煤层上覆岩层的垮落实际上是一个动态变化的过程,随着煤层的开采,上覆岩层开始垮落直到最终被完全压实,跨落到采空区的破碎岩体堆积起来形成地下水库,矿井水排入到地下水库中流动的过程涉及流固耦合渗流的问题,储水系数物性参数当然是动态变化的。结合大量工程案例,综合考虑各个采场的现场工程背景,可将煤层开采后的垮落带形状近似确定为抛物线形[5-6],即是煤层开采后上覆岩层垮落后垮落带的形状,以此可建立煤矿地下水库储水区示意图(图3)。
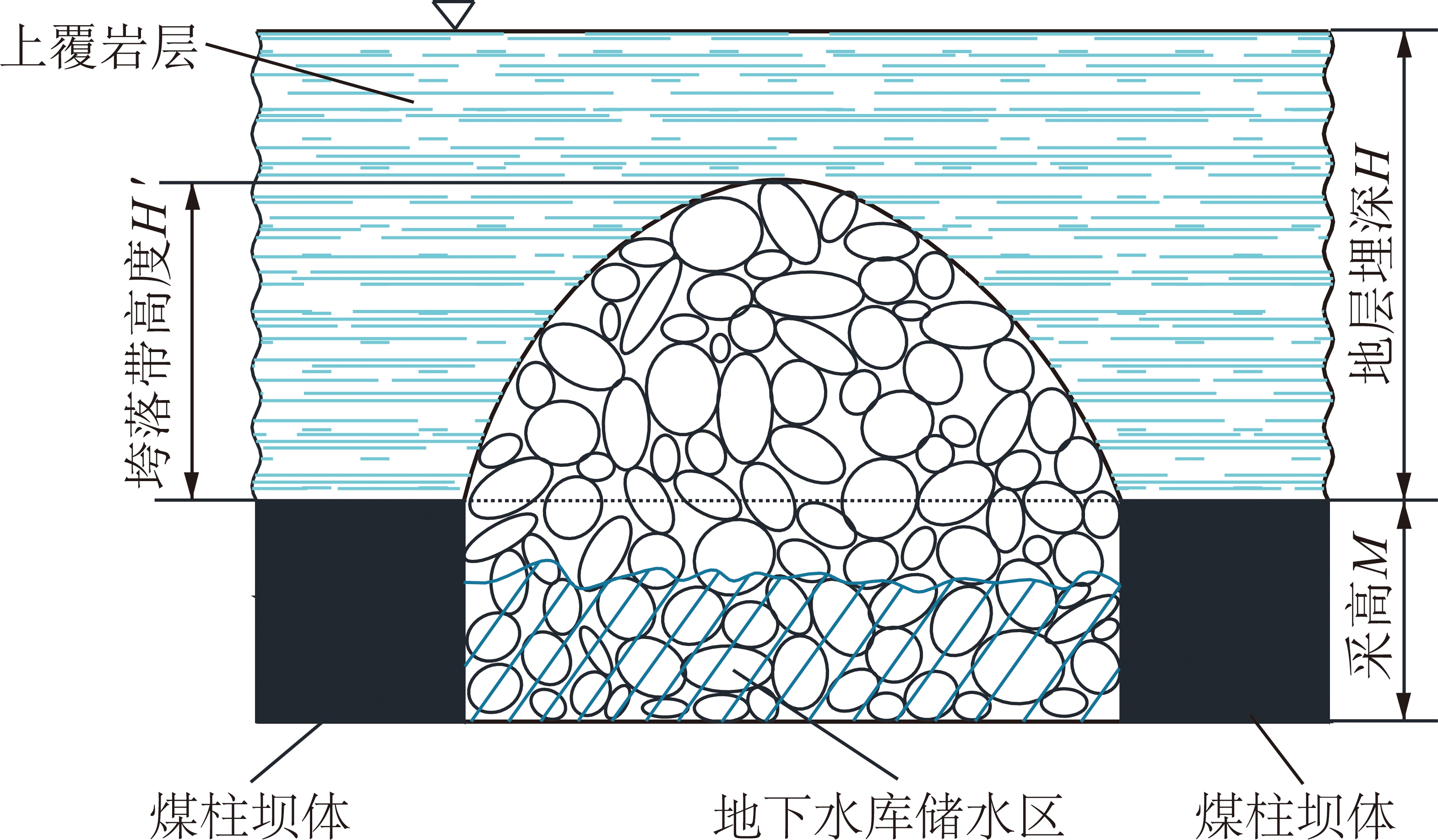
图3 煤矿地下水库储水区示意
Fig.3 Water storage area of coal mine underground reservoir
储水系数是采空区和垮落带内破碎岩体的空隙度。破碎岩体可视为多孔介质,大部分为可变形体[7]。在向采空区注入矿井水的过程中,由于空隙水压力的变化,一方面多孔介质骨架的Terzaghi有效应力会发生变化,从而导致储层渗透率、空隙度等特性发生变化。另一方面,这些变化又会反过来影响空隙水的流动和压力分布。因此,有必要建立考虑有效应力影响的储水系数流固耦合数学模型,来体现空隙流体流经多孔介质会影响其变形或强度的特点,即必须建立流固耦合中多孔介质内的应力场和空隙流体的渗流场方程。
2.1 应力场方程
基于多孔介质的有效应力原理[8-9]为
![]()
(1)
其中,σij为固体应力;r0为多孔介质孔隙度,在煤矿地下水库中,是指煤层顶板即煤层上覆岩层的初始储水系数;δij为克罗内克函数,当i=j时,δij=1,i≠j时,![]() 为固体颗粒之间的应力;p为空隙流体(水)的压力,令
为固体颗粒之间的应力;p为空隙流体(水)的压力,令![]() 为固体骨架的有效应力(Terzaghi有效应力)。则Terzaghi有效应力为
为固体骨架的有效应力(Terzaghi有效应力)。则Terzaghi有效应力为
σ′ij=σij-r0pδij
(2)
该原理可以体现多孔介质中的流固耦合效应[8-9],在煤矿矿井水流动问题中,可以认为是上覆岩层垮落后的破碎岩体变形和矿井水流动的耦合,即用于研究煤矿采空区和垮落带内处于散体状态岩体的储水能力。
根据弹性力学中应变-位移关系[10],几何方程可表示为
![]()
(3)
式中,εij为应变在x,y,z方向上的分量表达式;uj,i,ui,j为位移分量的矢量求导表达式。
假设多孔介质固体骨架为各向同性弹性体,则多孔介质有效应力-应变本构关系可以表述为
![]()
(4)
式中,εV为骨架体积应变,即下文所述上覆岩层破碎岩体的体应变;E为弹性模量;ν为泊松比。
应力平衡方程可以表述为
σij+fi=0
(5)
式中,fi为i方向上的体力分量,实际工程中认为fx=fy=0,fz=ρg,ρ为破碎岩体密度;g为重力加速度。
联立式(2),(5)可得
σ′ij+r0pδij+fi=0
(6)
将式(4)代入式(6)可以得到以基本未知量ux,uy,uz,r0,p为变量的平衡方程。
![]()
(7)
![]()
(8)
![]()
 2uz+
2uz+
![]()
(9)
式中, 2为拉普拉斯算子;ux,uy,uz分别为位移在x,y,z方向上的分量;fz为z方向上的体力分量。
2为拉普拉斯算子;ux,uy,uz分别为位移在x,y,z方向上的分量;fz为z方向上的体力分量。
2.2 渗流场方程
渗流发生在可变形的多孔介质中,因此不但骨架颗粒具有一定的渗流速度,而且流体也有一定的渗流速度,流体质点的速度为
vf=vr+vs
(10)
其中,vf为流体运动的绝对速度;vs为骨架颗粒运动的绝对速度;vr为流体相对于固体骨架颗粒的运动速度,即达西速度。根据定义可以得到各速度的表达式:
![]()
(11)
![]()
 p
p
(12)
式中,u为位移;t为时间;k为渗透率;μ为动力黏度; 为哈密顿算子。
为哈密顿算子。
当煤层开采时,流体为单相流体,属于饱和多孔介质,固体的连续性方程为

![]()
(13)
其中,ρs为地层密度,常数,因此式(13)可以被简化为

![]()
(14)
单相流体的连续性方程为

![]()
(15)
其中,ρf为流体密度,将式(10)~(14)代入式(15),可得
 (ρfvr)+2ρf
(ρfvr)+2ρf vs+vs
vs+vs
![]()
(16)
根据vs远小于vr,可以忽略式(16)左边的第2项和第3项,再将式(12)代入,简化后为

![]()
(17)
3 单维稳态储水系数求解方法
3.1 单维稳态储水系数计算
得到应力场和渗流场的基本方程之后,可以根据以下假设条件来确定储水系数R的解析解:① 矿井水注入采空区时,水库中没有水,空隙水压力等于大气压力,即矿井水的流动处于稳态;② 上覆岩层在空间上的压缩仅受重力作用,即考虑一维情况。煤层开采结束后,上覆岩层会发生垮落,令Vs,Vb,Vp分别为煤层上覆岩层岩体骨架体积,岩体外观体积,岩体空隙体积,各自相应的变化值为ΔVs,ΔVb,ΔVp,根据定义[8,11],可得
![]()
(18)
根据初始储水系数R0[11]的定义,可得
![]()
(19)
同理,由体积应变的定义,可得
![]()
(20)
在实际工程中,可认为煤层上覆岩层颗粒的破碎是弹性变形,那么导致变形的因素包括温度,空隙流体压力,结合采煤的实际情况,假设地层等温,可以不考虑温度场对变形的影响,由空隙流体压力变化引起的破碎岩体颗粒体积变化[8]为
ΔVs/Vs=-Δp/Ks
(21)
式中,Δp=p-p0,p0为初始空隙水压力,即水库无水时的大气压力;Ks为多孔介质骨架固体颗粒的体积弹性压缩模量。
在将矿井水注入采空区之前,意味着空隙水压力是恒定的,等于大气压力,即p=p0,即
Δp=0
(22)
根据假设条件,以一维稳态角度计算煤矿地下水库储水系数,即t=0,此时联立式(17)~(22),可以得到简化后煤矿地下水库储水系数的表达式为
![]()
(23)
此时,结合式(22)以及式(7)~(9),可以求解出x,y,z方向的Terzaghi有效应力分别为
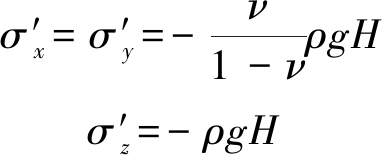
(24)
式中,H为煤矿地下水库所在煤层处于同一水平面的地层埋深值。
文献[10]指出,上覆岩层体应力σV会影响体应变εV的具体数值大小,即
![]()
(25)
综上可知,联立式(23),(25)可以得到单维稳态条件下考虑有效应力影响的煤矿地下水库储水系数R的计算公式
![]()
(26)
式(26)为依据储水系数定义和Terzaghi有效应力原理,综合考虑可能影响储水系数的各个因素,结合弹性力学、渗流力学的相关原理推导而来,理论性较强。需要确定的参数为煤矿地下水库储水区范围内破碎岩体的初始储水系数、煤层开采后上覆岩层的弹性模量、煤矿地下水库所在煤层上覆岩层的泊松比、煤层上覆岩层的密度、煤矿地下水库所在煤层处于同一水平面的地层埋深,下文对各参数确定进行详细说明。
3.2 相关参数确定
3.2.1 初始储水系数
煤矿地下水库储水区范围内破碎岩体的初始储水系数R0具体指的是煤矿地下水库刚建成时的初始储水系数,如果根据前文所述,采用定义来确定该数值显然不可取,为此,可以结合垮落带高度,提出实际可行的计算煤矿地下水库储水区范围内的初始储水系数R0的方法,如下文所述。
调研大量文献后发现,计算煤层上覆岩层冒落后的垮落带最大高度的方法有4种,分别是规程法,经验公式法,实践公式法,改进公式法,不同的方法优缺点不同,结合建设煤矿地下水库的实际背景,本文选择采用经验公式法和实践公式法确定垮落带最大高度,并结合具体算例分析比较两种方法的利弊,下面对两种方法进行简要叙述。垮落带高度示意如图4所示。
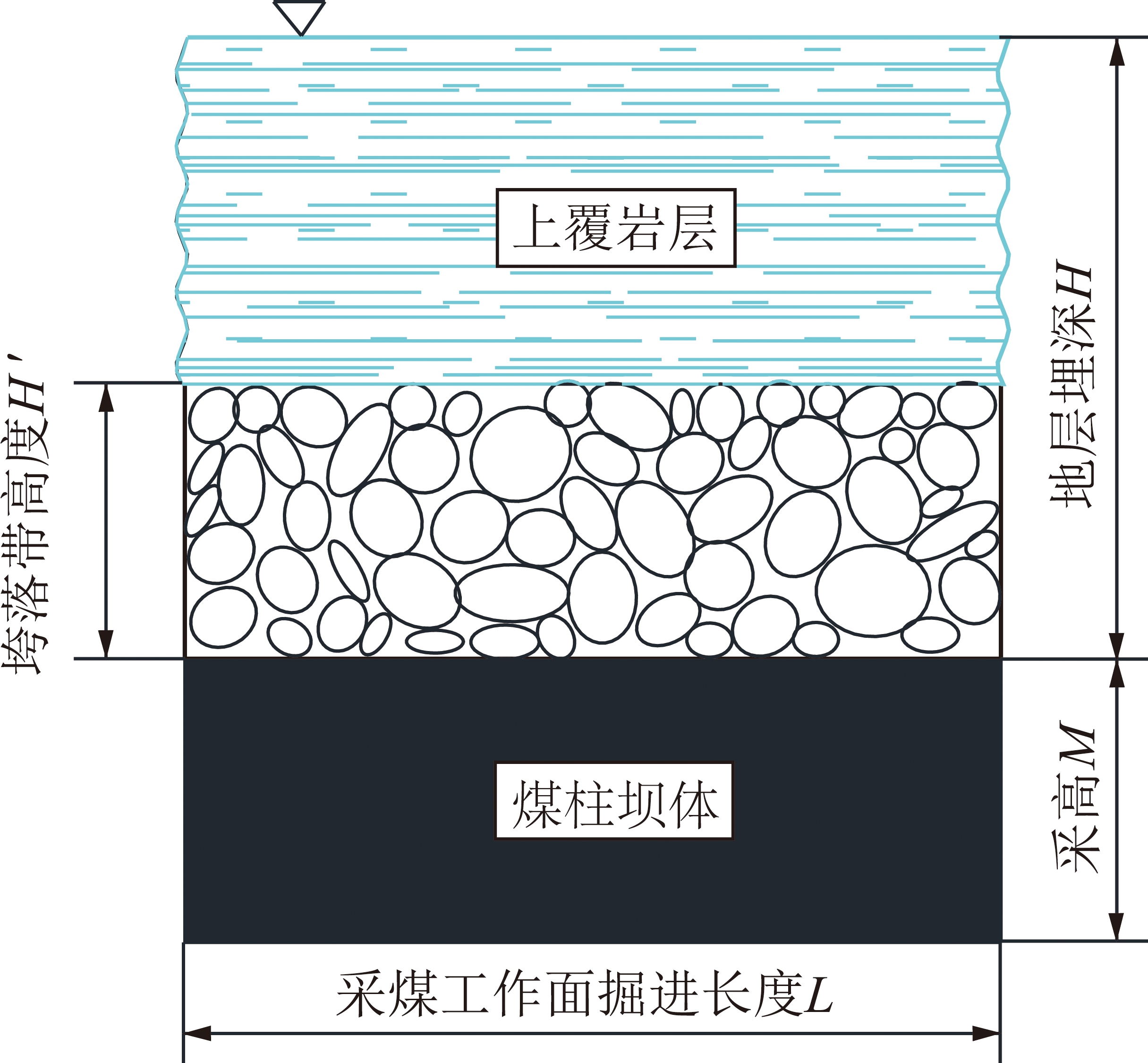
图4 垮落带高度示意
Fig.4 Height of the caving zone
(1)采用经验公式法[6,12-13]确定垮落带最大高度H′,即
H′=bM (上覆岩层为砂岩)
(27)
H′=cM (上覆岩层为砂质泥岩、泥岩)
(28)
式中,b,c均为常数,b的取值为4~5;c的取值为3~4;M为煤层采高。
(2)采用实践公式法[14-16]确定垮落带最大高度H′,即
![]()
(29)
式中,h为煤层厚度;Kp为岩石的碎胀系数;α为煤层倾角。
根据确定的煤层尺寸基本参数、采煤工作面基本尺寸参数以及垮落带最大高度H′,结合垮落带形状,可以根据数学中曲线拟合的思想大致拟合出垮落带形状的二次函数关系式;然后利用定积分的方法可以求得煤层上覆岩层冒落后垮落带范围内的截面面积St,截面面积按照式(30)计算:
St=dH′W
(30)
式中,d为积分常数,![]() 为采煤工作面宽度。
为采煤工作面宽度。
垮落带范围内的空间体积Vt为
Vt=LSt
(31)
式中,L为采煤工作面掘进长度。
然后,可以确定采煤工作面的截面面积Sk,即
Sk=WM
(32)
采煤工作面的空间体积Vk为
Vk=WML
(33)
由于要精确计算煤矿地下水库的储水系数,需要考虑任何可能改变储水系数的因素,煤层上覆岩层在煤层尚未开采前并不是完全没有空隙的,可能存在一定的空隙,如果不考虑该部分空隙体积,则会影响破碎岩体的初始储水系数的数值,最终会影响煤矿地下水库储水系数的数值,将煤矿地下水库所在煤层未开采前上覆岩层的初始储水系数r0纳入计算范围,更加符合计算的科学性。当煤层完全开采结束后,煤层上覆岩层跨落到采空区,可确定煤矿地下水库储水区范围内破碎岩体的初始储水系数R0,即
![]()
(34)
3.2.2 弹性模量
在煤层尚未进行开采时,可以通过具体实验或查资料的方法确定煤层上覆岩层即煤层顶板的弹性模量。根据大量实验数据表明,煤层开采后,煤层顶板岩体的弹性模量与开采前煤层顶板岩体的弹性模量存在如下关系:
E=aE0
(35)
式中,E0为煤层开采前煤层上覆岩层的弹性模量;E为煤层开采后煤层上覆岩层的弹性模量;a为常数,取值为0.2~0.6,通常取0.5。
3.2.3 泊松比
文献[17]中介绍,相同应变条件下,泊松比越大的煤样损耗能越大,这是由于泊松比较大的岩石材料内部横向结构变得松散,抗压强度随之减小,更容易破坏。可以推断出煤层上覆岩层的泊松比越大,会导致煤层开采结束后上覆岩层垮落到采空区的空隙度也越大,进而会影响煤矿地下水库储水系数的数值大小。
在建立煤矿地下水库之前,充分了解煤矿地下水库所在煤层未开采前上覆岩层的岩层特性,了解煤层上覆岩层组成成分,进行有关岩层组成成分的材料拉伸试验或者调研相关煤矿资料,确定煤矿地下水库所在煤层上覆岩层的泊松比ν,为计算储水系数提供数据支撑。
3.2.4 上覆岩层密度
不同的岩层各项物理力学参数不尽相同,根据煤矿地下水库所在煤层未开采前直接顶、基本顶的岩层特性,结合煤层上覆岩层岩性资料,确定煤层上覆岩层的密度值ρ,以及煤层上覆岩层的初始储水系数r0,r0一般情况下小于10%,该值可由岩性资料直接查出。
综合前文所述,首先确定式(26),(34)中的各参数值,然后将公式中有关参数的数值代入,通过式(26),(34)的具体计算,可实现对所有煤矿地下水库的储水系数进行理论计算,而且实用性很强,不受其他因素制约,可为实际工程计算提供帮助,可进一步精确了解所建煤矿地下水库的储水能力,更好的服务矿区用水,缓解矿区用水紧张的问题,为更好建设煤矿地下水库提供数据支撑。可以给出计算煤矿地下水库储水系数的流程图,如图5所示。
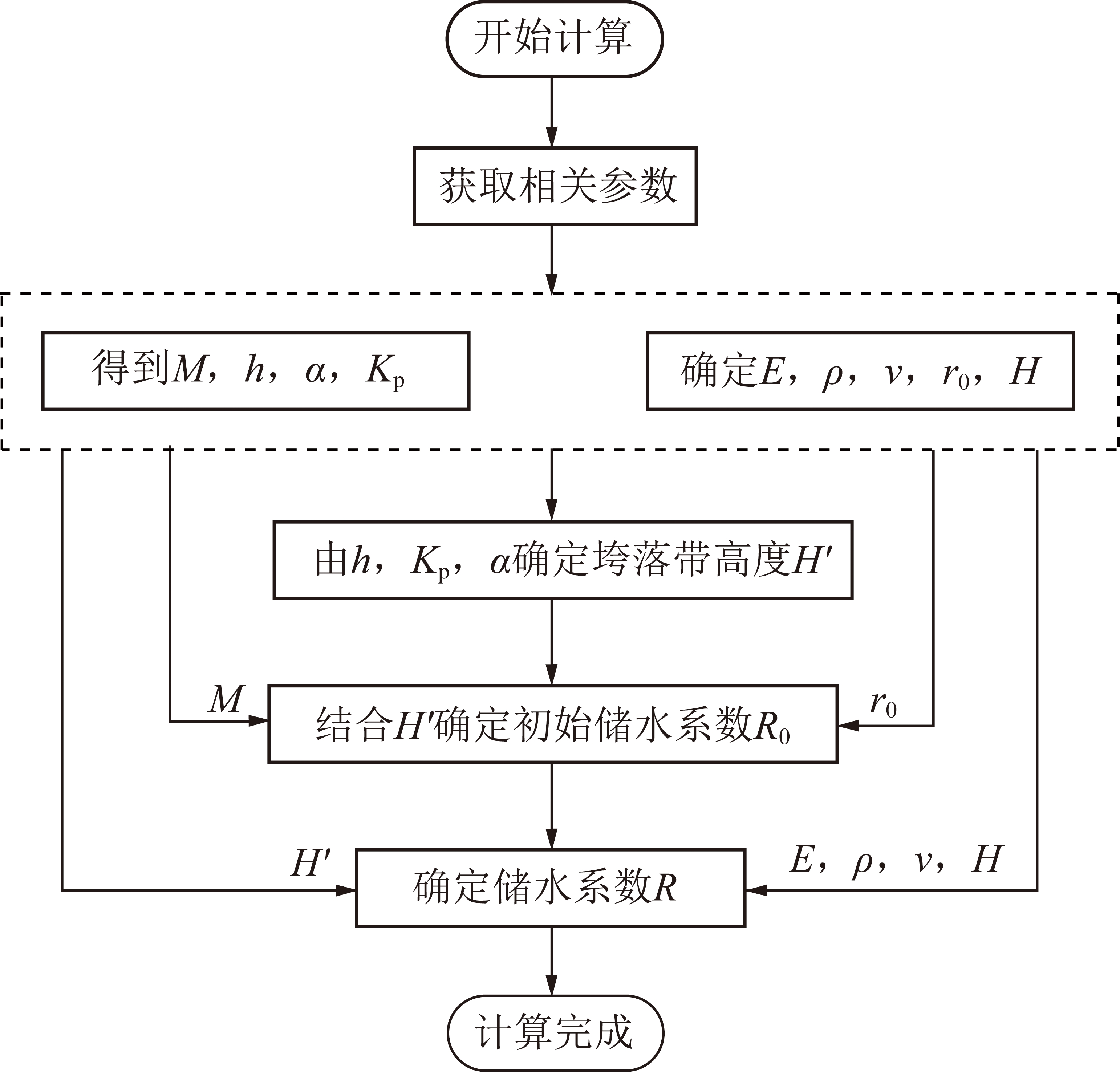
图5 煤矿地下水库储水系数计算流程
Fig.5 Calculation process of storage coefficient of underground reservoir in coal mine
4 实例计算及因素分析
依据所推导的公式,结合工程实例,对该计算方法进行算例分析。以宽沟煤矿[18-19]为例,结合所查找的资料与具体实验,确定宽沟煤矿B4-1煤层储水系数的各参数值,见表1。
表1 煤层物性参数
Table 1 Physical properties parameter of coal seam
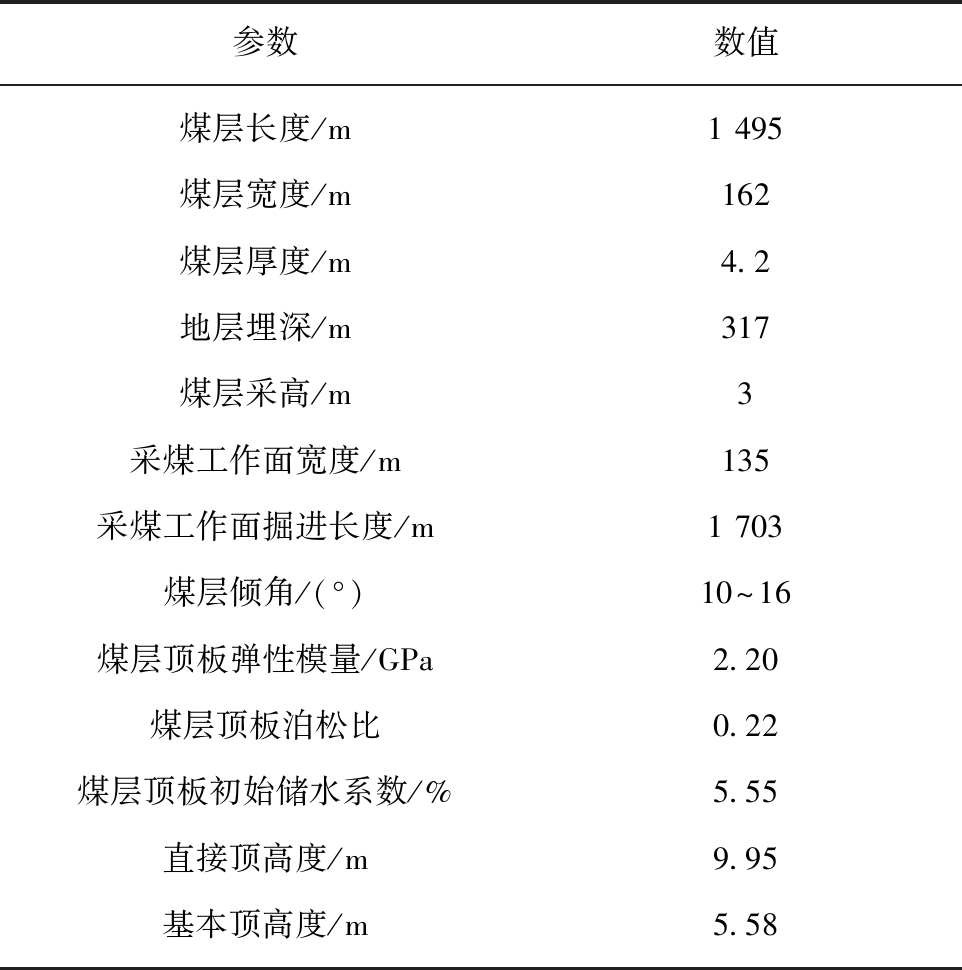
参数数值煤层长度/m1 495煤层宽度/m162煤层厚度/m4.2地层埋深/m317煤层采高/m3采煤工作面宽度/m135采煤工作面掘进长度/m1 703煤层倾角/(°)10~16煤层顶板弹性模量/GPa2.20煤层顶板泊松比0.22煤层顶板初始储水系数/%5.55直接顶高度/m9.95基本顶高度/m5.58
文献[19]中介绍,该煤层直接顶以泥岩、砂质泥岩为主,其次为粉砂岩,基本顶为粗砂岩,单向抗压强度为31 MPa,结合文献[15]中介绍的不同上覆岩层所受单向抗压强度以及主要岩石的名称,见表2,可以据此确定该煤层上覆岩性属于典型的中硬岩层岩性[20]。
当宽沟煤矿B4-1煤层完全开采后,结合所确定的这些数据,可以得知上覆岩层垮落且被压实后垮落带区域范围内破碎岩体的弹性模量E、上覆岩层的泊松比ν、煤层未开采前所受上覆岩层体应力σV,数值分别为
表2 上覆岩层岩性划分
Table 2 Lithology division of overlying strata
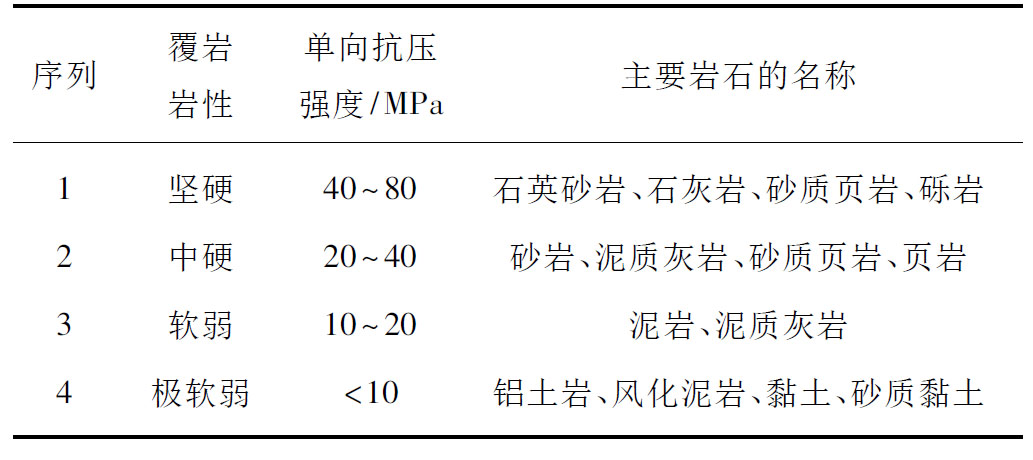
序列覆岩岩性单向抗压强度/MPa主要岩石的名称1坚硬40~80石英砂岩、石灰岩、砂质页岩、砾岩2中硬20~40砂岩、泥质灰岩、砂质页岩、页岩3软弱10~20泥岩、泥质灰岩4极软弱<10铝土岩、风化泥岩、黏土、砂质黏土
E=0.5×2.20=1.1 GPa
ν=0.22
-33 MPa
(36)
垮落带最大高度H′采用前文所述的两种方法进行计算:
(1)经验公式法。由于该煤层直接顶以泥岩、砂质泥岩为主,垮落带高度采用式(28)计算,可取c=4.33,则垮落带最大高度为H′=13 m。
(2)实践公式法。由于该煤层上覆岩层岩性属于典型的中硬岩层,文献[15]中介绍了常见岩石碎胀系数,见表3。
表3 常见岩石碎胀系数
Table 3 Bulking coefficient of common rocks

岩石名称坚硬岩石中硬岩石砂质黏土砂、砾石碎胀系数2.50~1.501.50~1.301.25~1.201.20~1.05
结合表1,3,取岩石碎胀系数Kp=1.4,煤层倾角α=13°,煤层厚度h=4.2 m,代入式(29),可以得到垮落带最大高度H′=11 m。
为了方便计算,在确定煤层开采后垮落带形状为抛物线形后,简化宽沟煤矿B4-1煤层垮落带形状并建立直角坐标系,如图6所示。
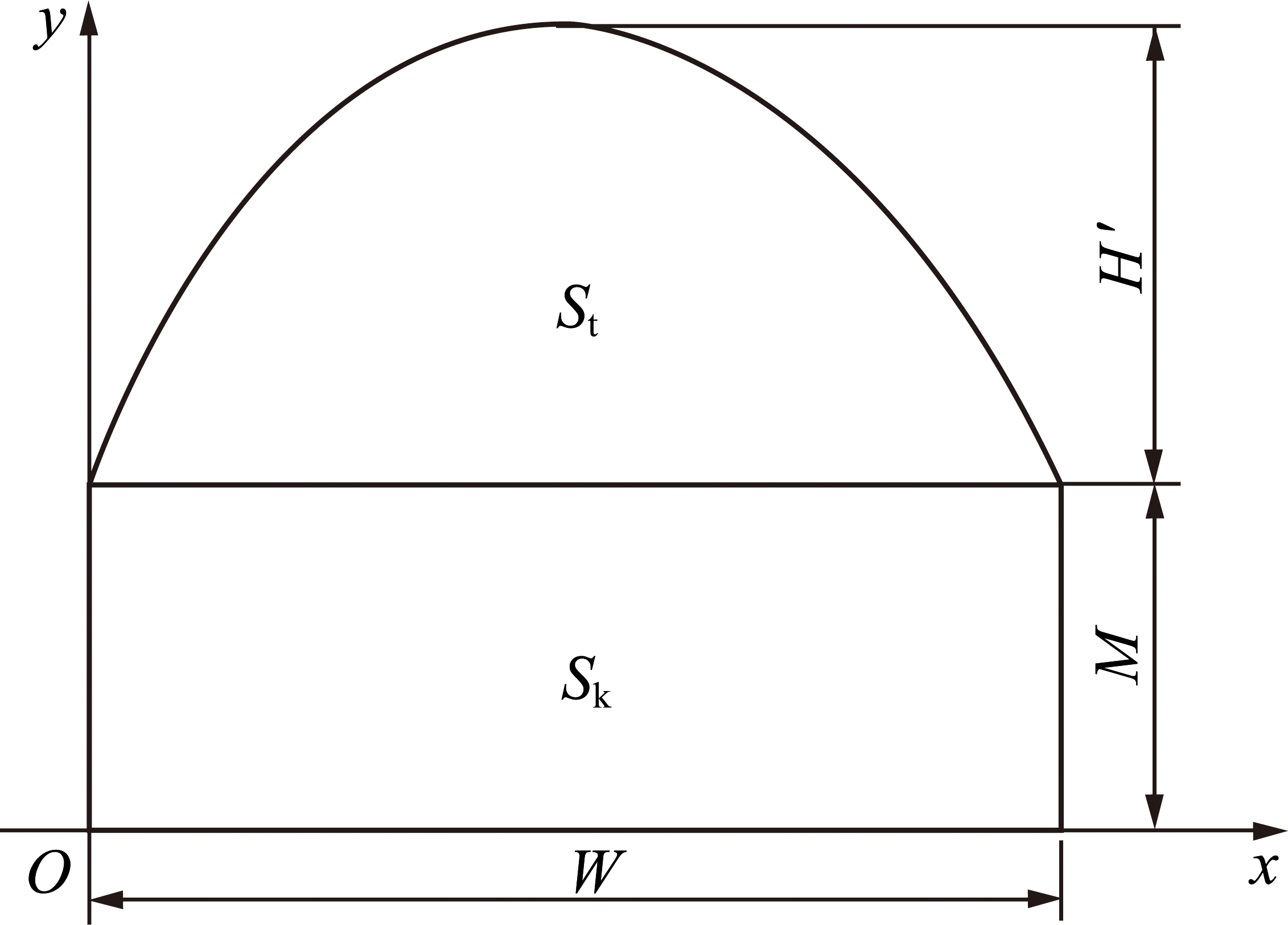
图6 垮落区和储水区面积示意
Fig.6 Caving area and the area of storage water
结合已经确定的基本数据,H′=13 m,可求得上覆岩层垮落后垮落带内的截面面积为![]()
垮落带范围内的空间体积为
Vt=LSt=1 703×1 170=1 992 510 m3
采煤工作面的截面面积为
Sk=WM=135×3=405 m2
采煤工作面的空间体积为
Vk=WML=135×3×1 703=689 715 m3
那么煤矿地下水库储水区范围内破碎岩体的初始储水系数:
当煤层上覆岩层完全垮落且岩层被压实后,可以得到宽沟煤矿B4-1煤层地下水库的储水系数为
[(1-0.22)×1.1×109×0.298 4-(1-2×
0.22)×(1+0.22)×6.76×103×9.8×317]/
[(1-0.22)×1.1×109-(1-2×0.22)×
(1+0.22)×6.76×103×9.8×317]=28.65%
再以H′=11 m计算宽沟煤矿B4-1煤层地下水库的储水系数R。同样的,可求得上覆岩层垮落后垮落带内的截面面积为:St=990 m2,则垮落带范围内的空间体积为:Vt=1 685 970 m3,采煤工作面的截面面积为:Sk=405 m2,采煤工作面的空间体积为:Vk=689 715 m3。
那么煤矿地下水库储水区范围内破碎岩体的初始储水系数R0=32.97%,宽沟煤矿B4-1煤层地下水库的储水系数R=31.83%。
4.1 弹性模量影响分析
下面以垮落带高度H′=13 m,进行Matlab编程数值计算,取R0=29.84%,ν=0.22,σV=-33 MPa,垮落后岩层的弹性模量取不同的数值,得到的结果如图7所示。由图7可知,在上覆岩层体应力处于定值时,垮落后的弹性模量越大,煤矿地下水库的储水系数越大,而且数值均小于冒落后的初始储水系数,表明煤层开采后,上覆岩层垮落直到完全被压实的过程中,储水系数呈减少趋势;弹性模量每增加1.1 GPa,储水系数增大的范围为0.4%~3.0%,平均1.7%。当弹性模量为定值时,随着上覆岩层体应力逐渐增大,破碎岩体体应变逐渐增大,由于体应变是以负值计算,故储水系数会逐渐减小。
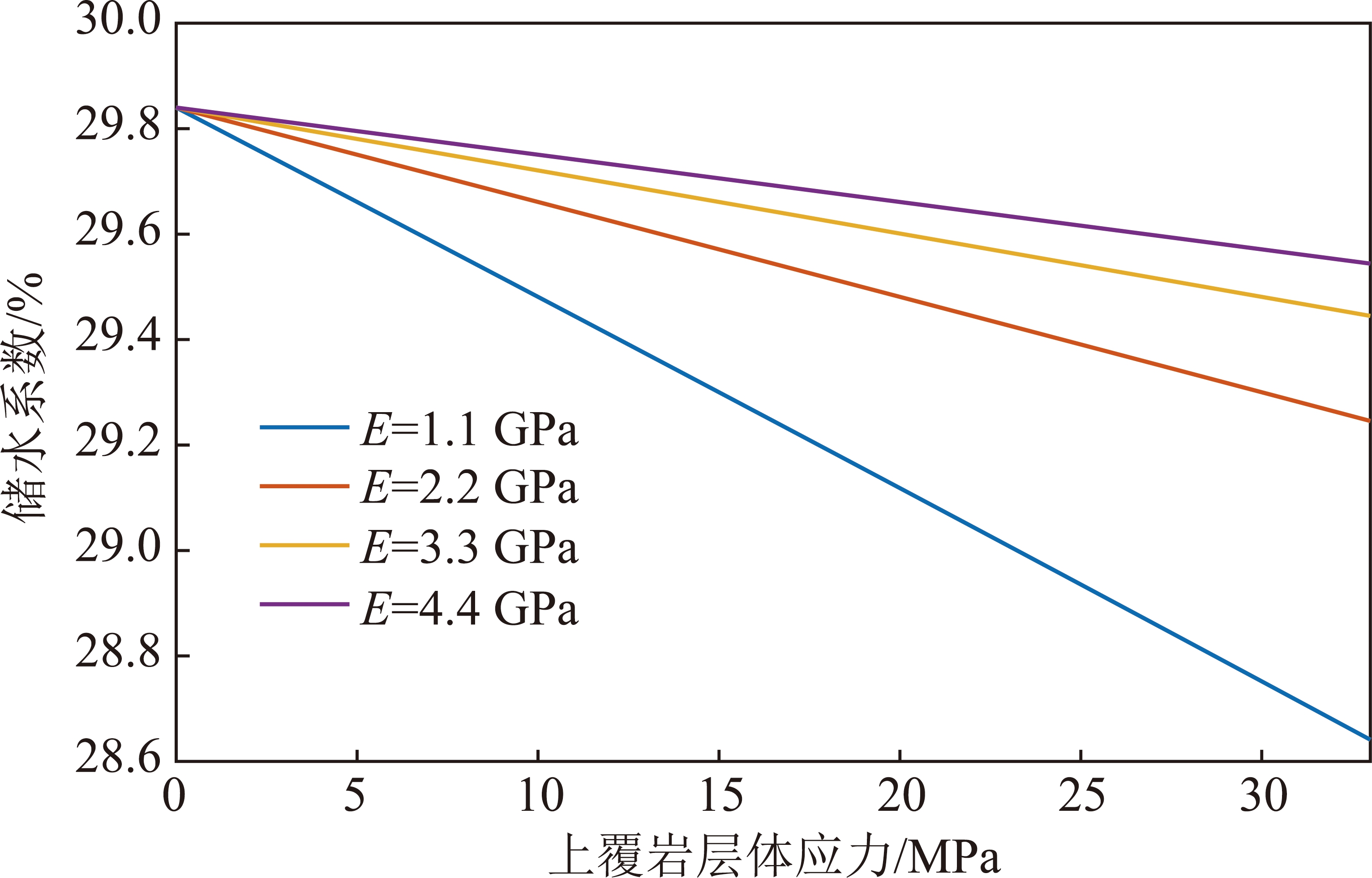
图7 不同弹性模量下上覆岩层体应力与储水系数的 变化关系
Fig.7 Relationship between overlying strata stress and storage coefficient under different elastic modulus

图8 不同上覆岩层体应力下弹性模量与储水系数的 变化关系
Fig.8 Relationship between elastic modulus and storage coefficient under different overlying strata stress
4.2 上覆岩层体应力影响分析
取R0=29.84%,ν=0.22,E=1.1 GPa,进行Matlab编程数值计算,上覆岩层体应力取不同的数值,得到如图8所示结果。在岩体处于同一弹性模量大小的情况下,上覆岩层体应力以负值计算,其值越大导致垮落后岩层的体应变越大,岩体被充分压实,没有较大空隙,因此垮落后岩层的储水系数逐渐减小;上覆岩层体应力越大,储水系数的变化范围也越大,其数值均小于初始储水系数;上覆岩层体应力每增加20 MPa,储水系数减小的范围为19%~39%,平均约29%。而且,弹性模量增大到一定值时,无论上覆岩层体应力怎么变化,储水系数的数值不再发生明显波动,说明此时煤层上覆岩层已经完全垮落,储水系数数值趋向于未垮落时的初始储水系数。可以发现,上覆岩层体应力对储水系数的影响较大,上覆岩层体应力主要改变破碎岩体的体应变,进而影响储水系数的数值大小。
4.3 泊松比影响分析
取R0=29.84%,σV=-33 MPa,E=1.1 GPa,进行Matlab编程数值计算,弹性模量取不同的数值,得到如图9所示结果。在同一泊松比的情况下,储水系数随垮落后岩层弹性模量的增大而增大,直至保持不变;在相同弹性模量的情况下,储水系数随泊松比的增大而增大;当上覆岩层体应力为定值时,泊松比对煤矿地下水库储水系数的影响呈曲线变化趋势。
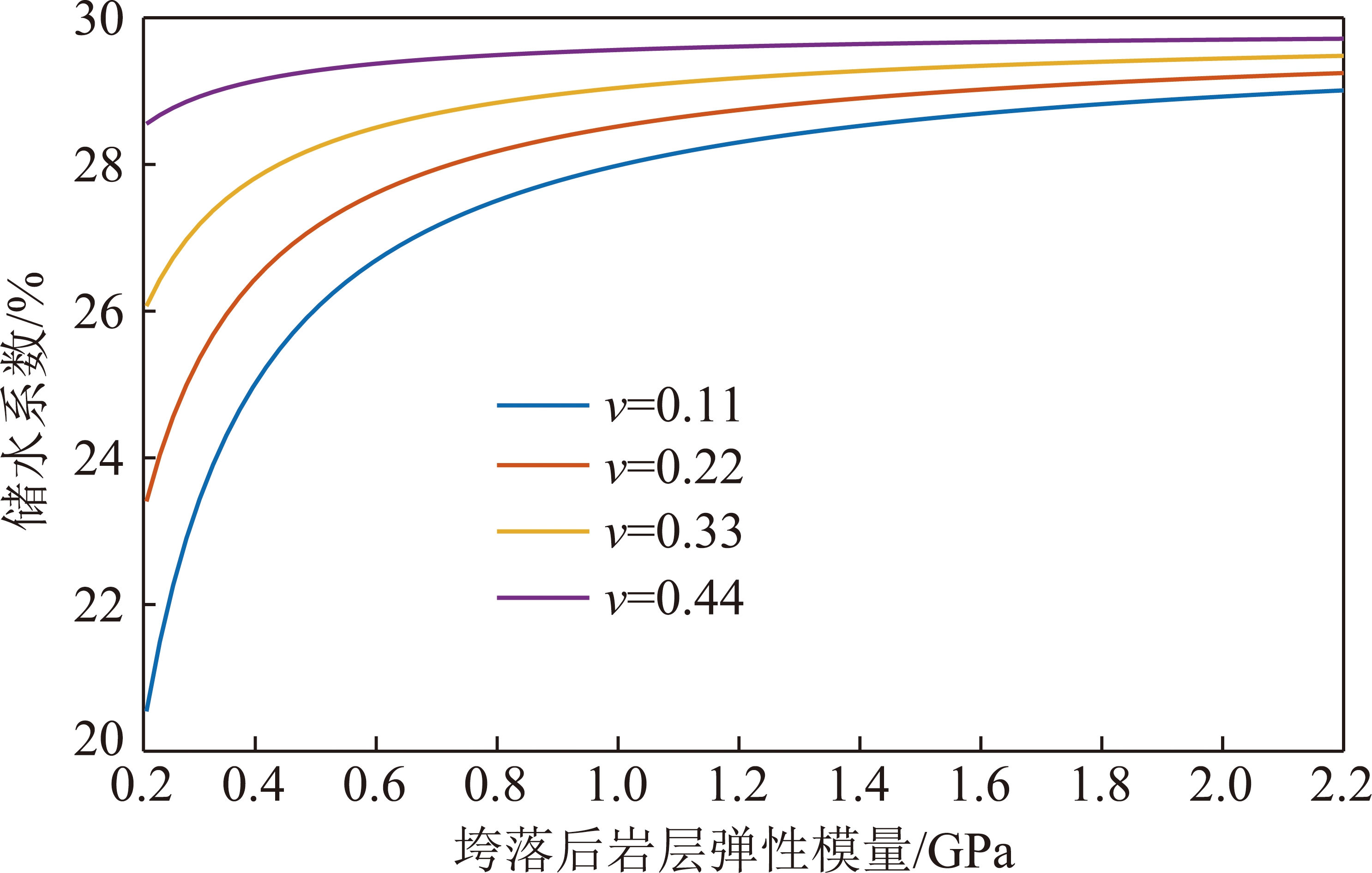
图9 不同泊松比情况下弹性模量与储水系数的变化关系
Fig.9 Relationship between elastic modulus and storage coefficient under different Poisson’s ratio
取R0=29.84%,σV=-33 MPa,E=1.1 GPa,进行Matlab编程数值计算,上覆岩层体应力取不同的数值,得到如图10所示结果。在同一泊松比的情况下,储水系数随上覆岩层体应力的增大而减小;在相同上覆岩层体应力的情况下,储水系数随泊松比的增大而增大;在弹性模量为定值时,泊松比对煤矿地下水库储水系数的影响呈线性变化趋势。综合图9,10可知,泊松比越接近0.5,储水系数将呈不变趋势;泊松比每增加0.1,储水系数增大10%~14%,平均12%。泊松比对煤矿地下水库储水系数的影响很大,不同于弹性模量和上覆岩层体应力对其影响,在实际工程中,应使储水系数保持不变。
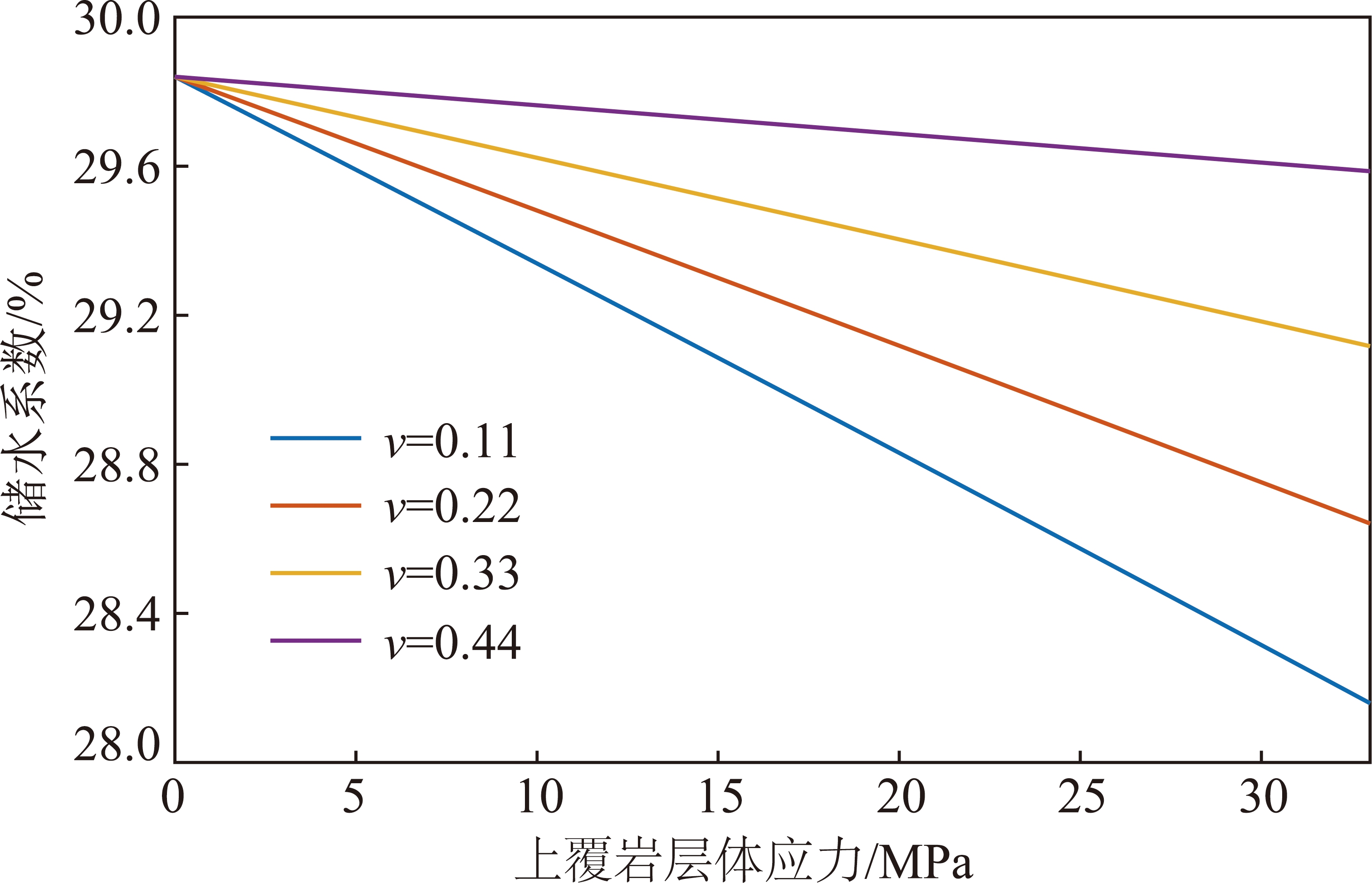
图10 不同泊松比情况下上覆岩层体应力与储水系数的 变化关系
Fig.10 Relationship between overlying strata stress and storage coefficient under different Poisson’s ratio
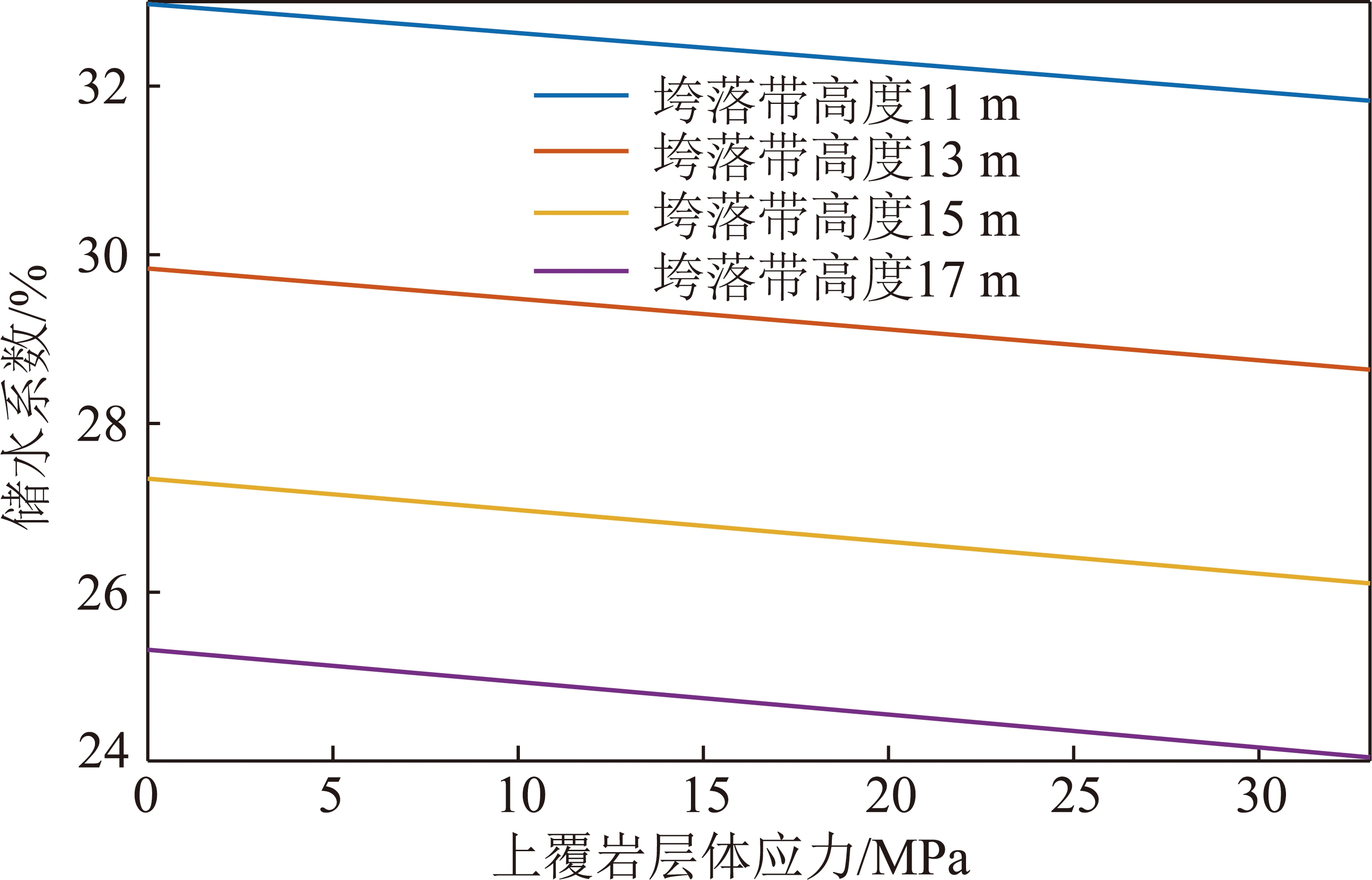
图11 不同垮落带高度情况下上覆岩层体应力与储水系数的 变化关系
Fig.11 Relationship between overlying strata stress and storage coefficient under different height of caving zone
4.4 垮落带高度影响分析
取σV=-33 MPa,E=1.1 GPa,ν=0.22,M=3 m,结合该煤层上覆岩层初始储水系数r0=5.55%,进行Matlab编程数值计算,上覆岩层体应力取不同的数值,得到如图11所示结果。在上覆岩层体应力处于定值时,可以发现,储水系数随着垮落带高度的增大而减小,说明垮落带高度越高,煤层上覆岩层冒落后的空间体积会越大,在空隙体积一定的情况下,会导致储水系数变小;垮落带高度每增加2 m,储水系数减小的范围为8%~11%,平均10%;当垮落带高度为定值时,随着上覆岩层体应力的增大,破碎岩体的体应变也越大,由于上覆岩层体应力以负值计算,故会导致储水系数逐渐减小。
4.5 采高影响分析
取σV=-33 MPa,E=1.1 GPa,ν=0.22,H′=3 m,结合该煤层上覆岩层初始储水系数r0=5.55%,进行Matlab编程数值计算,上覆岩层体应力取不同的数值,得到如图12所示结果。由图12可知,在采高处于定值的情况下,储水系数的大小随上覆岩层体应力的增大呈减小趋势,最终基本保持不变;在上覆岩层体应力处于定值的情况下,采高越高,上覆岩层破碎后的空隙体积越大,会导致储水系数随之增大,采高每增加1 m,储水系数增大20%~60%,平均约40%。在采煤时,应该根据煤层赋存情况,确定最佳采煤方法,保证采高高度的合理性,进而为储水系数的计算提供数据保障。
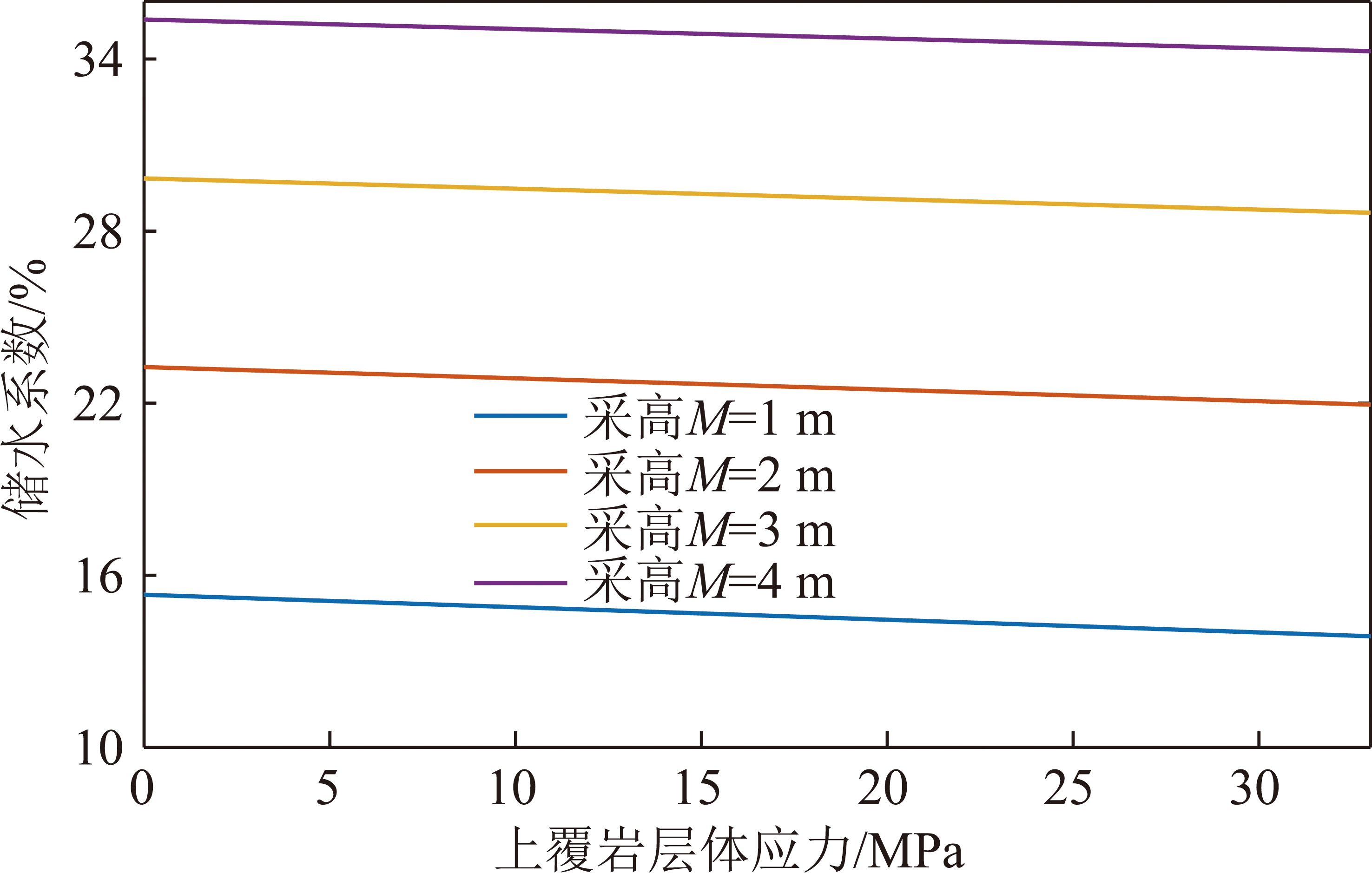
图12 不同采高情况下上覆岩层体应力与储水系数的 变化关系
Fig.12 Relationship between overlying strata stress and storage coefficient under different mining height
对比各因素对煤矿地下水库储水系数的影响可知,上覆岩层体应力、泊松比以及垮落带高度和采高对储水系数数值影响较大,在实际工程计算与应用中,应该使储水系数保持不变,便于水库的安全监测与科学管理,更好的服务矿区用水问题。
5 结 论
(1)煤层开采后,当上覆岩层刚开始垮落到完全被压实的过程中,上覆岩层的弹性模量在逐渐变小;影响煤矿地下水库储水系数的因素包括:煤层上覆岩层弹性模量、上覆岩层密度、地层埋深、上覆岩层体应力、上覆岩层初始储水系数、泊松比、采高、垮落带高度。
(2)随着弹性模量的逐渐增大,储水系数的数值呈曲线趋势增大,弹性模量每增加1.1 GPa,储水系数增大0.4%~3%;随着上覆岩层体应力的逐渐增大,储水系数的数值呈线性趋势减小,上覆岩层体应力每增加20 MPa,储水系数减小19%~39%;但各自的储水系数数值均小于煤矿地下水库储水区范围内破碎岩体的初始储水系数;当弹性模量增大到某一值时,储水系数将不随其他因素的改变而改变,储水系数数值趋于一定值。
(3)当泊松比接近0.5时,无论弹性模量以及上覆岩层体应力怎么改变,储水系数都将呈不变趋势;储水系数会随着垮落带高度的增大而减小,垮落带高度每增加2 m,储水系数减小8%~11%;储水系数会随着采高的增大而增大,采高每增加1 m,储水系数增大20%~60%。
(4)根据各个因素对储水系数变化平均范围的影响程度,可得到采高对储水系数的影响最大,上覆岩层体应力次之,弹性模量最小;岩石物性参数泊松比对储水系数的影响迥异,在计算时不能忽略。
[1] 张国恩.煤矿地下水库人工挡水坝安全性分析[J].中国煤炭,2014,40(S1):78-81,86.
ZHANG Guoen.Safety analysis of artificial dam in underground reservoir of coal mine[J].China Coal,2014,40(S1):78-81,86.
[2] 顾大钊.煤矿地下水库理论框架和技术体系[J].煤炭学报,2015,40(2):239-246.
GU Dazhao.Theory framework and technological system of coal mine underground reservoir[J].Journal of China Coal Society,2015,40(2):239-246.
[3] 陈苏社.神东矿区井下采空区水库水资源循环利用关键技术研究[D].西安:西安科技大学,2016:61-62.
CHEN Sushe.Research on the key technology of water resources recycling utilization in the underground goaf reservoir in Shendong Mining Area[D].Xi’an:Xi’an University of Science and Technology,2016:61-62.
[4] 李全生,鞠金峰,曹志国,等.基于导水裂隙带高度的地下水库适应性评价[J].煤炭学报,2017,42(8):2116-2124.
LI Quansheng,JU Jinfeng,CAO Zhiguo,et al.Adaptability evaluation of underground reservoir based on height of water flowing fractured zone[J].Journal of China Coal Society,2017,42(8):2116-2124.
[5] 向鹏,孙利辉,纪洪广,等.大采高工作面冒落带动态分布特征及确定方法[J].采矿与安全工程学报,2017,34(5):861-867.
XIANG Peng,SUN Lihui,JI Hongguang,et al.Dynamic distribution characteristics and determination method of caving zone in large mining height working face[J].Journal of Mining and Safety Engineering,2017,34(5):861-867.
[6] 王兆丰,李青松,杨利平,等.下石节矿综放工作面上覆岩层位移冒落带高度确定的研究[J].煤,2007(1):1-3.
WANG Zhaofeng,LI Qingsong,YANG Liping,et al.Recearch of determination of height of displacement caving zone of overlying strata in fully mechanized top coal caving face of Xiashijie mine[J].Coal,2007(1):1-3.
[7] JAMTVEIT B,HAMMER Ø.Sculpting of rocks by reactive fluids[J].Geochemical Perspectives,2012,1(3):341-481.
[8] 李培超,孔祥言,卢德唐.饱和多孔介质流固耦合渗流的数学模型[J].水动力学研究与进展(A辑),2003,18(4):419-426.
LI Peichao,KONG Xiangyan,LU Detang.Mathematical model of fluid solid coupling seepage in saturated porous media[J].Journal of Hydrodynamics Ser.A,2003,18(4):419-426.
[9] TERZAGHI K.Theorerical Soil Mechanics[M].New York:Wiley,1943,265-267.
[10] 徐芝纶.弹性力学简明教程(第三版)[M].北京:高等教育出版社,1990:364-369.
[11] 冉启全,李士伦.流固耦合油藏数值模拟中物性参数动态模型研究[J].石油勘探与开发,1997(3):61-65,100.
RAN Qiquan,LI Shilun.Research on dynamic model of physical parameters in fluid solid coupling reservoir numerical simulation[J].Petroleum Exploration and Development,1997(3):61-65,100.
[12] 吕波.冒落带与裂隙带最大高度及充水系数值的计算[J].能源技术与管理,2013,38(3):55-56.
LÜ Bo.Calculation of the maximum height of the caving zone and fissure zone and the numerical value of water filling coefficient[J].Energy Technology and Management,2013,38(3):55-56.
[13] 李华奇,刘鹏程.采空区冒落带高度影响因素及分布规律分析[J].煤炭技术,2011,30(8):117-119.
LI Huaqi,LIU Pengcheng.Analysis of Influencing factors and distribution regularities of caving zone heights[J].Coal Technology,2011,30(8):117-119.
[14] 郭杉.马堡煤矿8206工作面“三带”高度确定[J].同煤科技,2016(6):17-22.
GUO Shan.“Three zones” height determination of,8206 working face in Mabao Coal Mine[J].Tong Mei Ke Ji,2016(6):17-22.
[15] 张文俊,张彪,徐慧钢,等.新元煤矿3号煤层冒落带与裂隙带高度研究[J].能源技术与管理,2018,43(1):78-80.
ZHANG Wenjun,ZHANG Biao,XU Huigang,et al.Research on height of caving zone and fissure zone in No.3 coal seam of Xinyuan coal mine[J].Energy Technology and Management,2018,43(1):78-80.
[16] 张发亮,何启林.工作面上覆岩冒落导水裂隙两带高度的确定[J].矿业工程研究,2012,27(4):66-70.
ZHANG Faliang,HE Qilin.Research on two zones heights for caving and permeable fracture zone of overlying strata of working face[J].Mineral Engineering Research,2012,27(4):66-70.
[17] 杨英明.动力扰动下深部高应力煤体冲击失稳机理及防治技术研究[D].北京:中国矿业大学(北京),2016:71-72.
YANG Yingming.Mechanism and prevention technology of coal bumps for highly-stressed coal in deep mining under dynamic disturbance[D].Beijing:China University of Mining and Technology(Beijing),2016:71-72.
[18] 孙雪亮,杜涛涛,李红平,等.宽沟煤矿E1148(1)工作面初次放顶技术研究[J].煤炭科技,2014(1):5-7.
SUN Xueliang,DU Taotao,LI Hongping,et al.Study on the first caving technology of E1148(1) working face in Kuan Gou Coal Mine[J].Coal Science and Technology Magazine,2014(1):5-7.
[19] 李浩荡,蓝航,杜涛涛,等.宽沟煤矿坚硬厚层顶板下冲击地压危险时期的微震特征及解危措施[J].煤炭学报,2013,38(S1):6-11.
LI Haodang,LAN Hang,DU Taotao,et al.Micro-seismic characteristic and danger-relief method in rock-burst danger period of mining face under hard and thick roof of Kuangou Coal Mine[J].Journal of China Coal Society,2013,38(S1):6-11.
[20] 陈晓龙.宽沟煤矿冲击地压防治研究[D].西安:西安科技大学,2012:16-17.
CHEN Xiaolong.Research on prevention of pressure bump in Kuangou Coal Mine[D].Xi’an:Xi’an University of Science and Technology,2012:16-17.
