随着“一带一路”战略的逐步实施，寒区岩土工程建设的数量及规模将大幅度增加[1]。寒区工程结构的岩石一直承受着昼夜及季节交替的冻融循环作用，且处于一定的应力场中，受赋存环境的作用，岩石内部的微观缺陷会不断产生、扩展，其损伤累积的宏观效应表现为岩石的变形破坏。因此，在冻融-荷载作用的条件下研究岩石的损伤本构模型，反映岩石变形破坏的全过程，对寒区工程建设具有重要的理论和工程意义。
冻融岩石力学特性的研究一直是寒区岩土工程领域的热点问题。YAVUZ H等[2]通过12种碳酸盐岩的冻融循环及物理力学特性试验，利用多元回归分析法得到岩石的劣化模型;HUSEYIN Y[3]对安山岩进行热冲击循环和冻融循环试验，并测试其硬度、波速和抗压强度;BAYRAM F[4]对采自土耳其9个地区的石灰岩进行冻融循环和单轴压缩试验，得到与岩石弹性模量、吸水率及冲击强度相关的统计模型;PARK J等[5]对饱水凝灰岩、闪长岩、玄武岩进行了冻融循环试验，采用SEM和CT技术分析冻融过程中岩石的微结构变化;徐光苗等[6]开展岩石的冻融循环和力学特性试验，揭示冻融破坏机制;陈有亮等[7]通过冻融循环和单轴压缩试验，探究初始损伤等因素的影响规律;张慧梅等[8-9]开展了岩石的冻融循环及力学特性试验，建立了冻融损伤模型;袁小清等[10]建立了一维应力状态下冻融节理岩体的损伤本构模型;申艳军等[11-12]通过试验探讨冻融循环温度、冻融时长、循环次数对岩石力学参数影响规律，并分析不同缺陷形态引起的岩体内部冻胀力发生机制;王劲翔等[13]进行了饱水英安岩的冻融循环、电镜扫描和抗压强度试验，表明冻融作用导致岩石内部裂隙扩展，岩石强度参数逐渐减弱;周科平等、李杰林等[14-15]对冻融后的花岗岩进行了核磁共振测试和常规单轴压缩实验，得到岩石的孔隙度和单轴抗压强度关系式。
目前对冻融岩石力学特性的研究主要在实验层面上，涉及冻融损伤模型的研究较少。模型多基于Lemaitre应变等价原理建立，能较好地描述冻融岩石峰前应变行为，不能有效描述峰后段尤其是残余变形阶段特征，未能从岩石损伤的细观力学响应揭示其宏观变形特征。
笔者在冻融-荷载共同作用的条件下，对应变等价性原理进行修正，推导出可反映残余强度特征的岩石损伤模型;开展红砂岩冻融循环及三轴压缩试验，验证模型的合理性;分析岩石细观损伤演化特征及其宏观力学效应。
1 基于残余强度特征的冻融损伤模型
1.1 应变等价原理的修正
应变等价原理认为，岩石所受荷载均由未损伤部分承担，因此当岩石完全损伤时，残余强度必然为0。实际上，岩石进入峰后破坏阶段之后，承载力逐渐丧失，此时，岩石内部形成宏观破裂面，其承载力即为破裂面之间的摩擦力，不再随着变形的增加而改变，称为残余强度。因此，岩石内部损伤的微元仍具有一定的承载力[16-18]。为了建立基于残余强度特性的岩石损伤模型，假定:
(1)将冻融受荷岩石分为冻融损伤、受荷损伤、冻融与荷载共同损伤及未损伤4部分，共同承担轴向应力。
(2)岩石完全破坏后，其轴向应力由冻融损伤、受荷损伤、冻融与荷载共同损伤3部分承担，且岩石的承载力立刻降为残余强度;岩石未完全破坏时，未损伤部分的本构关系遵循广义虎克定律，表示为
(1)
式中，
分别为轴向方向岩石未损伤部分的有效应变及有效应力；
为侧向方向岩石未损伤部分的有效应力；En，μn为岩石经历n次冻融循环后的弹性模量和泊松比。
(3)不考虑侧方向的残余强度，即侧方向的荷载均由未损伤部分承担。其损伤本构关系可基于应变等价原理得出。
1.2 损伤本构模型的建立
选取如图1所示的岩石微元，在轴向方向，设岩石总面积为A，微元所承受的总名义应力及应变分别为σ1，ε1，其中岩石未损伤部分所受有效应力为
对应的微元面积为A1;3个损伤部分所受总应力为残余应力σr。
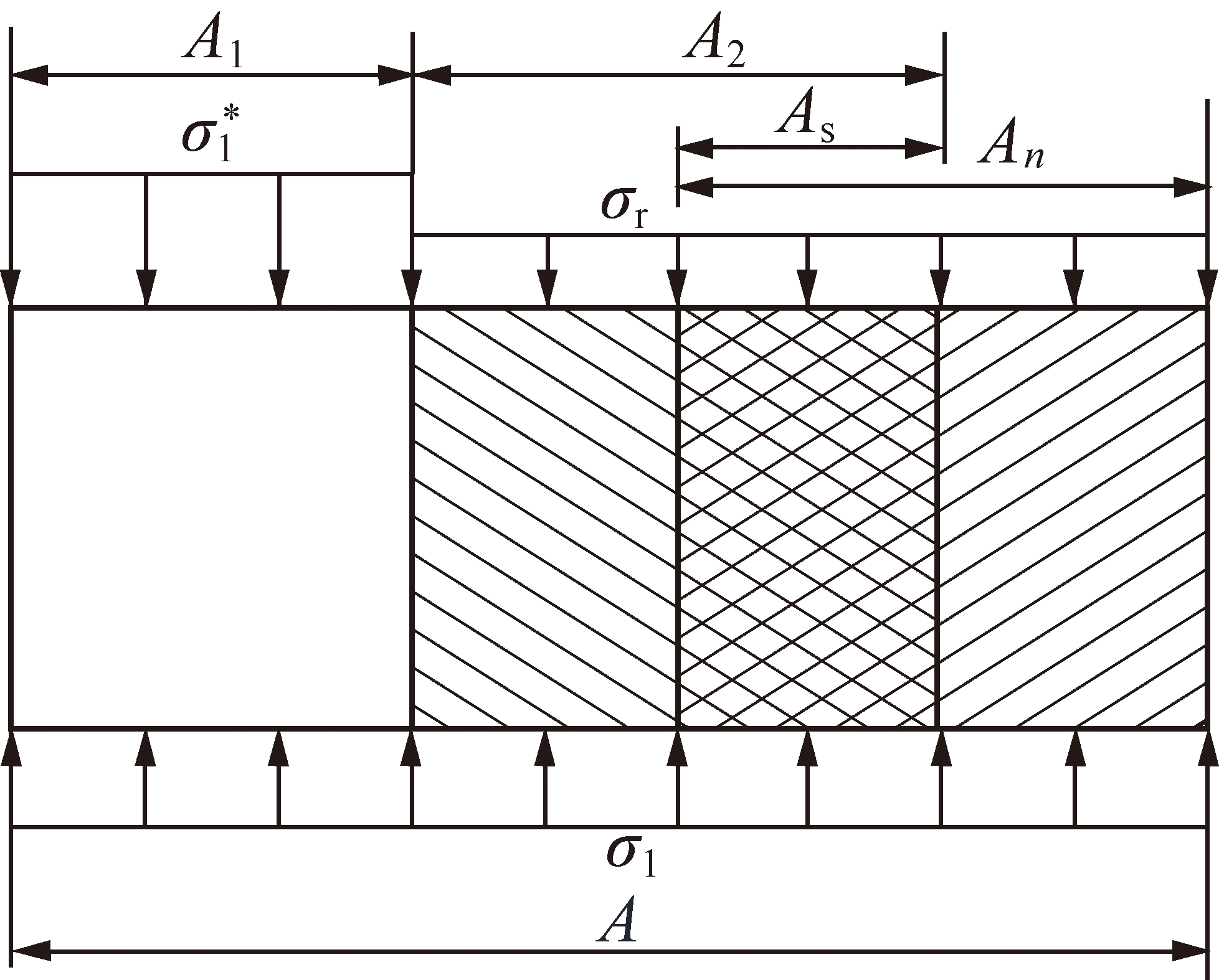
图1 岩石微元轴向受力
Fig.1 Micro-element axial force diagram of rock
设岩石受冻融循环作用后，冻融损伤面积为An，定义冻融损伤变量
(2)
经历冻融循环后的岩石，受到荷载的作用进一步产生损伤。设受荷损伤部分面积为A2，其中冻融与荷载共同损伤面积为As。定义冻融岩石的受荷损伤变量
(3)
总体考虑，冻融受荷岩石的总损伤变量Dm可根据其最终损伤程度定义
(4)
由式(2)～(4)得到Dm计算公式为
Dm=D+Dn-DDn
(5)
式(5)表征了冻融与荷载导致的2种损伤与总损伤之间的非线性关系。
根据假定(1)可得
(6)
A=A1+An+A2-As
(7)
由式(5)～(7)可得
(8)
根据岩石微元损伤与未损伤部分变形协调关系可得
(9)
又由假定(3)可得
(10)
于是，将式(9)，(10)代入式(1)可得
(11)
将式(11)代入式(8)可得
σ1=Enε1(1-Dm)+N1Dm+μn(σ2+σ3)
(12)
式中，N1=σr-μn(σ2+σ3)。
假设岩石破坏的概率密度函数服从Weibull分布，荷载作用下其损伤变量D可表示为
(13)
式中，F*为岩石微元强度随机分布变量;P(F*)为概率密度函数;m与F0为Weibull分布参数。
冻融循环作用使岩石宏观力学性能劣化，可用弹性模量作为度量损伤的参量，则Dn定义冻融损伤变量
(14)
式中，E0为经历冻融循环之前岩石的弹性模量。
将式(13)，(14)代入式(5)，得到冻融-荷载作用下岩石的总损伤变量
(15)
由式(12)，(15)可得常规三向应力状态下，冻融受荷岩石基于残余强度特征的损伤本构模型
(16)
式中，
为岩石微元强度轴向的随机分布变量。
为了合理度量式(16)中的岩石微元强度，假定岩石破坏服从D-P准则，其分布变量可表示为
(17)
式中，
为岩石特性参数;φn为岩石经历n次冻融循环后的内摩擦角;
分别为有效应力张量的第一不变量、有效应力偏量的第二不变量，表达式为
(18)
(19)
在常规三向应力状态下，将式(10)，(11)和式(18)，(19)代入式(17)中可得
(20)
式中，
根据假定(3)，侧方向的损伤本构关系可基于应变等价原理[9]得出
(21)
式中，微元强度侧方向的随机分布变量
为
(22)
式(16)，(21)即为本文所建冻融-荷载作用下考虑残余强度特征的岩石损伤本构模型。
2 模型参数的确定
若用σcn和εcn分别表示n次冻融循环之后某一围压下岩石应力-应变曲线的峰值应力和峰值应变，则存在如下几何条件:
将ε1=εcn，σ1=σcn代入式(16)，得参数F0和m的表达式
(23)
式中，
为峰值处对应的值。
将σi(i=1,3)视为关于εi(i=1,3)和n的函数[9]，则σ1的全微分形式为
(24)
对式(16)，(21)分别求全微分得到
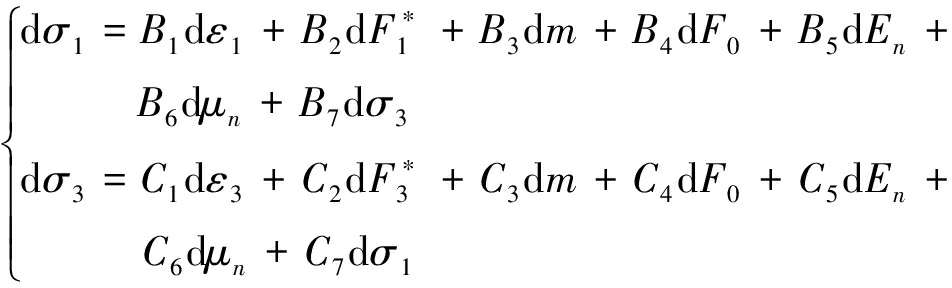
(25)
式中，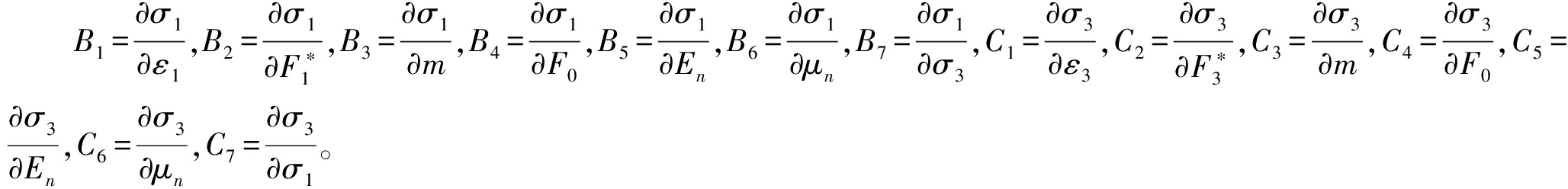
根据式(20)，(22)，将式(25)中的
进一步求全微分变为仅含dε1,dε3,dσ1,dσ3,dn项的形式
(26)
式中，
假定F0,m,En和μn仅为应力σ3和n的函数[9]，则有
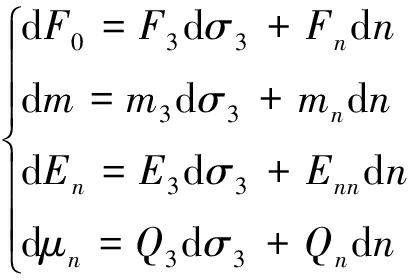
(27)
式中，
将式(26)，(27)代入式(25)并替换得到
(28)
式中，U1=B2F12-1，U2=B2F14+B3mn+B4Fn+B5Enn+B6Qn，U3=B2F13+B3m3+B4F3+B5E3+B6Q3+B7，U4=B1+B2F11，W1=C2F22+C7，W2=C2F24+C3mn+C4Fn+C5Enn+C6Qn，W3=C2F23+C3m3+C4F3+C5E3+C6Q3-1，W4=C1+C2F21。
解方程组(28)得到dσ1的表达式，再与式(25)比较，根据几何条件
可得
(29)
式中，
解式(29)可得
(30)
联立式(23)和(30)得到
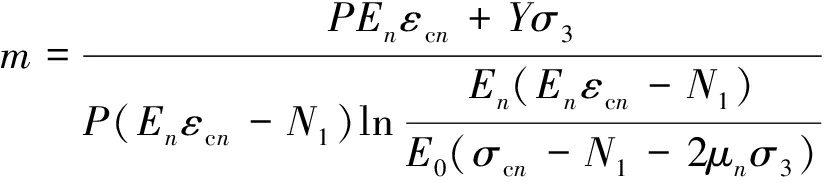
(31)
(32)
式(31)，(32)即为模型参数的理论表达式。由式(15)，(20)，(31)，(32)可得岩石总损伤演化方程
(33)
式中，
由式(33)可知，当岩石应变、应力及冻融循环状态变化时，其总损伤演化率方程为
(34)
式(34)表明了岩石总损伤扩展的3种途径及其对岩石损伤的影响。
由式(16)，(20)，(31)，(32)可得考虑残余强度特征的冻融岩石损伤本构模型
(35)
3 冻融损伤模型验证
3.1 冻融岩石力学特性试验
将红砂岩加工成直径50 mm，高100 mm的标准圆柱体试样，先将试样置于冻融循环试验机实施开放饱水状态的冻融循环试验，再对经过0，5，10，20，40次冻融作用后的试样进行4种围压下的三轴压缩试验。得到各种冻融循环及围压下的应力-应变试验曲线如图2所示。其中，围压为0时红砂岩的破坏以脆性为主，残余强度值不易获取。由图2可知，岩石变形破坏全过程大致经历了压密、弹性、塑性屈服、应变软化及残余变形阶段。
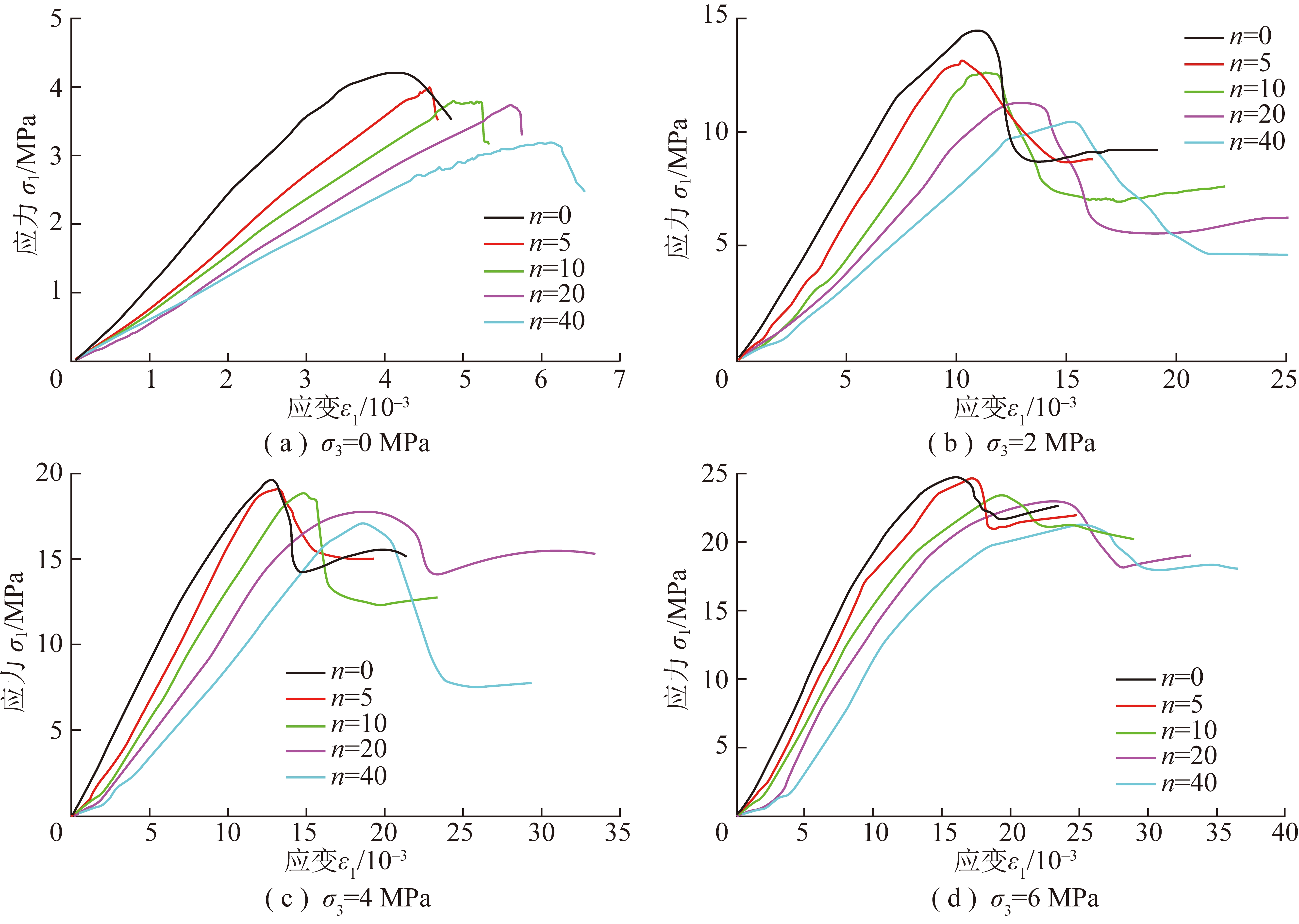
图2 岩石应力-应变试验曲线
Fig.2 Stress-strain experimental curves of rock
随着冻融次数及围压强度的增加，岩石的压缩性逐渐增强，峰值应变不断增大，塑性屈服段非线性特征愈来愈明显，应力-应变曲线峰后应力下降速率变慢，岩石由脆性破坏模式逐渐转变为延性破坏模式。但其他参数指标如弹性模量、弹性极限、峰值应力及残余强度随着冻融次数的增大而减小，随着围压强度的增大而增大。
3.2 模型验证
利用图2的试验结果，由式(35)计算可得各种围压及冻融循环条件下岩石损伤模型理论曲线。图3选取了4种代表性理论曲线，并与试验曲线对比。
由图3可知，本文所建损伤模型的理论曲线与试验曲线吻合较好，可以反映岩石变形破坏的全过程，从而验证了本构方程及损伤变量描述的合理性。
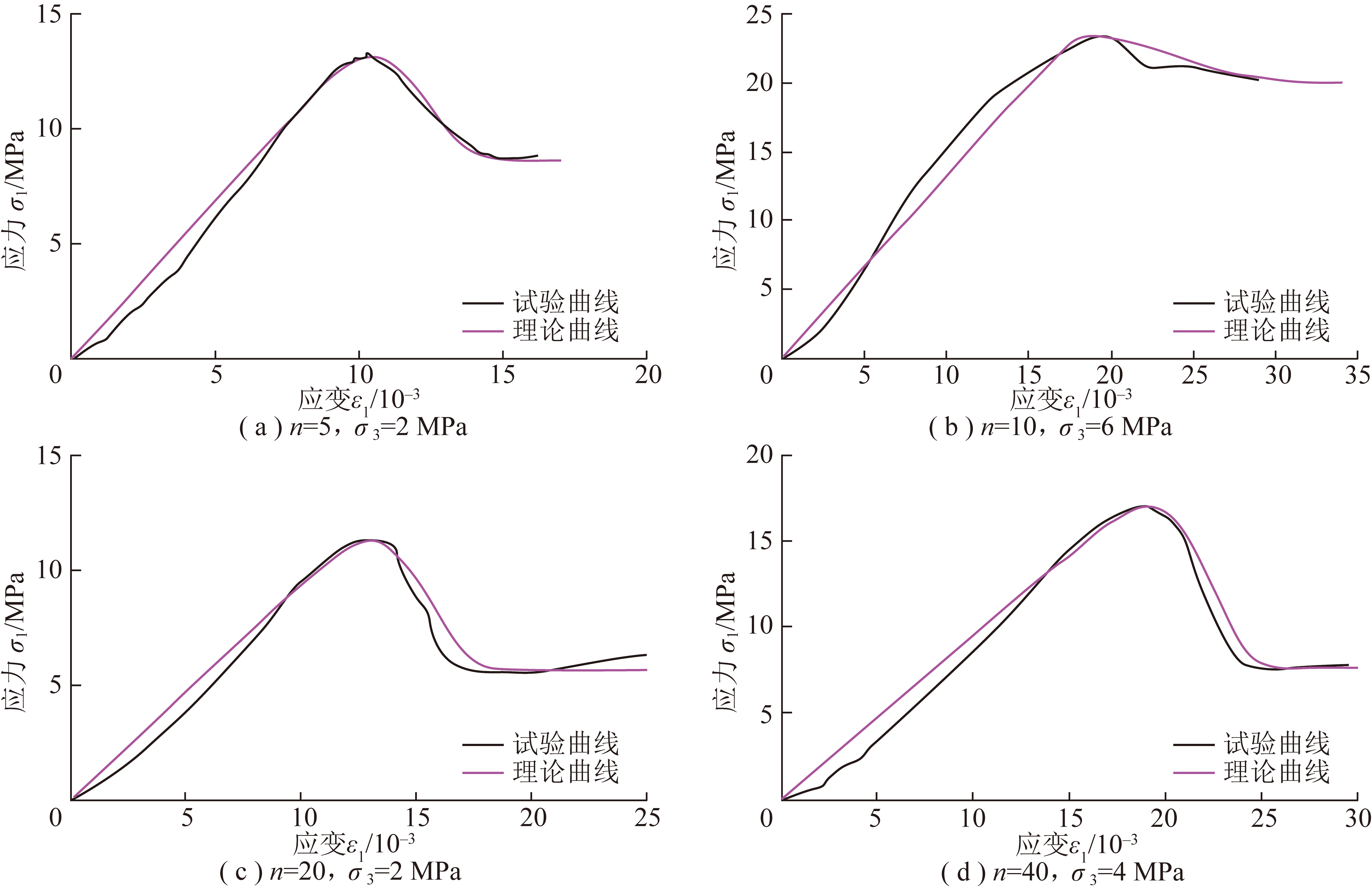
图3 岩石本构模型理论与试验曲线比较
Fig 3 Comparison between test and theoretical curves of constitutive model for rock
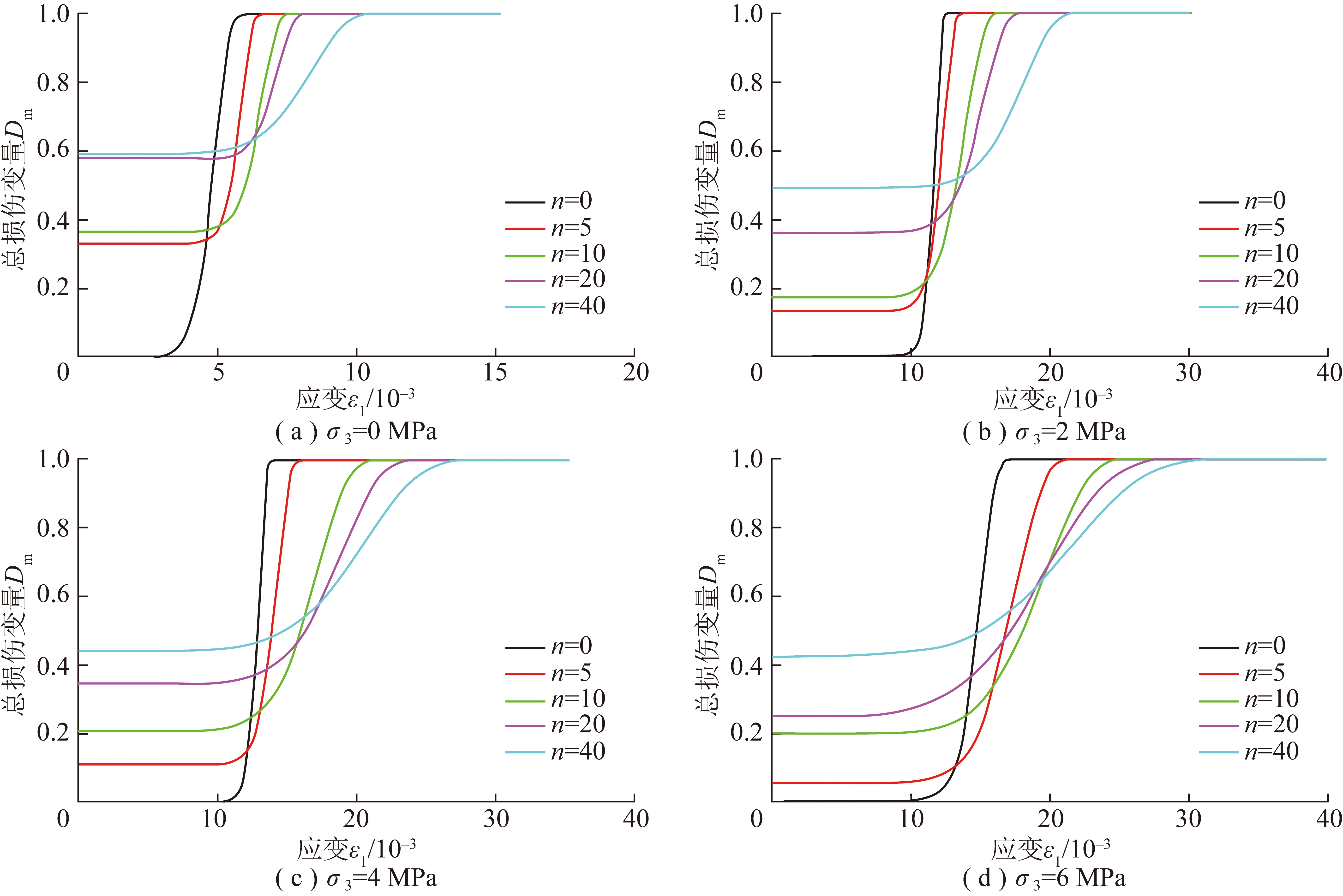
图4 岩石总损伤演化曲线
Fig.4 Total damage evolved curves of rock
4 冻融-荷载作用下岩石损伤力学特性
由式(33)及图2的试验数据进行计算，得出岩石冻融受荷总损伤演化曲线如图4所示。
由图4可知，损伤演化图形均呈S型曲线，能很好地反映岩石压缩变形的各阶段:① 压密及弹性变形阶段。对应受荷初期损伤演化曲线近水平段，损伤变量几乎不变。此时，岩石裂隙圧密闭合但并未扩展，微元产生弹性变形。② 塑性变形阶段。对应损伤演化曲线的上凹段，损伤变量迅速上升。此时，裂隙开始扩展且速度加快，岩石产生塑性屈服。③ 应变软化阶段。对应损伤演化曲线的上凸段，曲线斜率逐渐减小。此时，裂隙不断扩展、贯通，岩石强度逐步丧失。④ 残余变形阶段。岩石内部出现宏观破裂面而完全破坏，损伤变量趋于1，并保持不变。
如图4所示，随着冻融循环次数的增加，相同应变值所对应的损伤变量增大，说明冻融循环引起的岩石矿物晶粒不均匀缩胀及水冰相变使损伤劣化程度加剧，宏观上表现出岩石刚度及强度的减小;但在岩石变形的中后期，损伤演化曲线先后相交，相交之后反而表现出损伤变量随着冻融次数的增加而减小，宏观上表现为岩石抵抗变形能力的减弱，塑性变形及延性破坏特征更加显著。
随着围压增大，同一应变值对应的损伤变量值依次变小，说明围压能够抑制损伤的演化，使其刚度和强度等宏观特征参量增大;同时，相同损伤程度时，岩石的应变不断增长，即岩石损伤累积的增长速度逐渐变缓，岩石的塑性特性渐次增强，破坏方式转变为延性破坏。
根据图2的试验数据，由式(33)，(34)计算得到岩石冻融受荷总损伤演化率曲线，如图5所示。
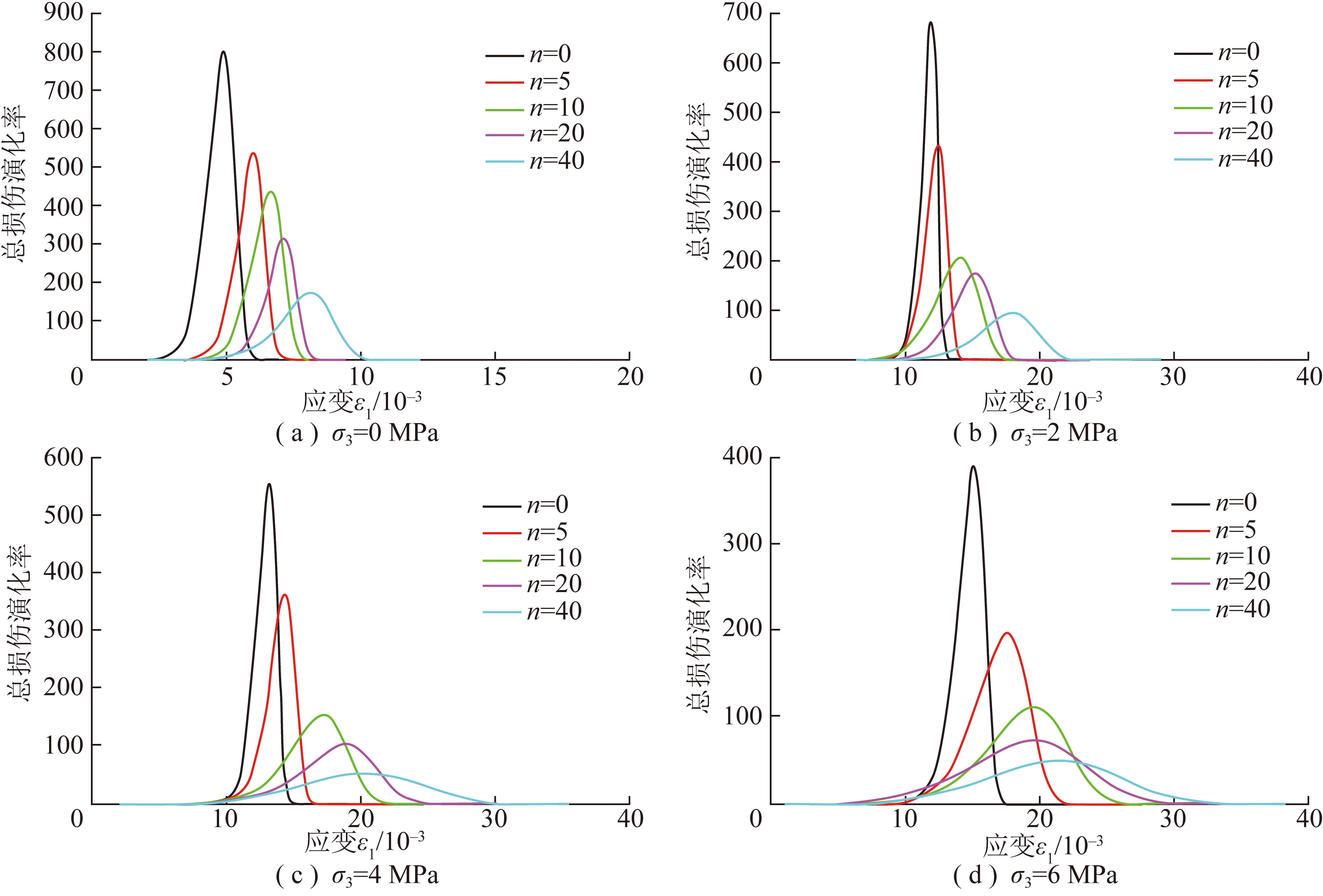
图5 岩石损伤演化率曲线
Fig.5 Damage evolved ratio curves of rock
由图5可知,损伤演化率曲线均呈抛物线形状，亦可以较好地反映出岩石变形的各个阶段。随着冻融次数或围压的增大，曲线峰后段下降坡度逐次变缓，峰值点降低，而峰值点处的轴向应变却在增加，说明冻融循环和围压的作用使岩石损伤演化速率减缓，岩石的塑性特征增强，其破坏形式逐渐趋向延性破坏。
本文损伤模型所揭示的岩石损伤扩展规律及其所预测的宏观力学性质与冻融岩石力学特性试验结果吻合，进一步说明了损伤模型的合理性。
5 结 论
(1)将冻融受荷岩石分为未损伤、冻融损伤、受荷损伤、冻融与荷载共同损伤4部分，其中损伤部分承受残余应力。基于损伤统计理论，建立了基于残余段变形特征的冻融受荷岩石损伤本构模型，推导了模型参数的理论表达式。
(2)开展红砂岩冻融循环力学特性试验验证模型的合理性，结果表明，本文所建模型可以反映岩石变形破坏全过程及冻融循环和围压对岩石力学特性的影响。模型参数的理论表达式表述了岩石冻融损伤的内在机制与其特征参量的一般规律。
(3)岩石的损伤演化途径反映了细观力学响应与宏观变形破坏过程相一致。随着围压的增大，岩石刚度及强度增大，塑性特征增强。冻融循环使岩石损伤劣化程度加剧，宏观上表现为岩石刚度及强度减小，塑性变形及延性破坏特征更加明显。
[1] 刘慧,刘卫东.“一带一路”建设与我国区域发展战略的关系研究[J].中国科学院院刊,2017,32(4):340-347.
LIU Hui,LIU Weidong.Study on relationship between the belt and road initiative and regional development strategies of China[J].Journal of Chinese Academy of Sciences,2017,32(4):340-347.
[2] YAVUZ H,ALTINDAG R,SARAC S,et al.Estimating the index properties of deteriorated carbonate rocks due to freeze-thaw and thermal shock weathering[J].International Journal of Rock Mechanics & Mining Sciences,2006,43(5):767-775.
[3] HUSEYIN Y.Effect of freeze-thaw and thermal shock weathering on the physical and mechanical properties of an andesite stone[J].Bulletin of Engineering Geology and the Environment,2011,70(2):187-192.
[4] BAYRAM F.Predicting mechanical strength loss of natural stones after freeze-thaw in cold regions[J].Cold Regions Science and Technology,2012,83-84(12):98-102.
[5] PARK J,HYUN C U,PARK H D.Changes in microstructure and physical properties of rocks caused by artificial freeze-thaw action[J].Bulletin of Engineering Geology and the Environment,2015,74(2):555-565.
[6] 徐光苗,刘泉声.岩石冻融破坏机理分析及冻融力学试验研究[J].岩石力学与工程学报,2005,24(17):3076-3082.
XU Guangmiao,LIU Quansheng.Analysis of mechanism of rock failure due to freeze-thaw cycling and mechanical testing study on frozen-thawed rocks[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3076-3082.
[7] 陈有亮,代明星,刘明亮,等.含初始损伤岩石的冻融损伤试验研究[J].力学季刊,2013,34(1):74-80.
CHEN Youliang,DAI Mingxing,LIU Mingliang,et al.Experimental investigation on freezing damage characteristics of granite with initial damage[J].Chinese Quarterly of Mechanics,2013,34(1):74-80.
[8] 张慧梅,杨更社.冻融岩石损伤劣化及力学特性试验研究[J].煤炭学报,2013,38(10):1756-1763.
ZHANG Huimei,YANG Gengshe.Experimental study of damage deterioration and mechanical properties for freezing-thawing rock[J].Journal of China Coal Society,2013,38(10):1756-1763.
[9] 张慧梅,谢祥妙,彭川,等.三向应力状态下冻融岩石损伤本构模型[J].岩土工程学报,2017,39(8):1444-1452.
ZHANG Huimei,XIE Xiangmiao,PENG Chuan,et al.Constitutive model for damage of freeze-thaw rock under three-dimensional stress[J].Chinese Journal of Geotechnical Engineering,2017,39(8):1444-1452.
[10] 袁小清,刘红岩,刘京平.冻融荷载耦合作用下节理岩体损伤本构模型[J].岩石力学与工程学报，2015,34(8):1602-1611.
YUAN Xiaoqing,LIU Hongyan,LIU Jingping.A damaging model of jointed rock under coupled action of freezing and thawing[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1602-1611.
[11] 申艳军,杨更社,荣腾龙,等.岩石冻融循环试验建议性方案探讨[J].岩土工程学报,2016,38(10):1775-1782.
SHEN Yanjun,YANG Gengshe,RONG Tenglong,et al.Proposed scheme for freeze-thaw cycle tests on rock[J].Chinese Journal of Geotechnical Engineering,2016,38(10):1775-1782.
[12] 申艳军,杨更社,王婷,等.岩石内孔隙/裂隙冻胀力模型及其适用性评价[J].冰川冻土,2019,41(1):117-128.
SHEN Yanjun,YANG Gengshe,WANG Ting,et al.Evaluation of frost heave force models of pore/fissure in rock and their applicability[J].Journal of Glaciology and Geocryology,2019,41(1):117-128.
[13] 王劲翔,丁军浩,邓辉,等.冻融循环条件下英安岩的物理力学特性试验研究[J].科学技术与工程,2017,17(17):304-309.
WANG Jinxiang,DING Junhao,DENG Hui,et al.Experimental study on physical and mechanical properties of rock under the condition of freeze-thaw cycles[J].Science Technology and Engineering,2017,17(17):304-309.
[14] 周科平,许玉娟,李杰林,等.冻融循环对风化花岗岩物理特性影响的实验研究[J].煤炭学报,2012,37(S1):70-74.
ZHOU Keping,XU Yujuan,LI Jielin,et al.Experimental study of freeze and thawing cycle influence on physical characteristics weathered granite[J].Journal of China Coal Society,2012,37(S1):70-74.
[15] 李杰林,周科平,柯波.冻融后花岗岩孔隙发育特征与单轴抗压强度的关联分析[J].煤炭学报,2015,40(8):1783-1789.
LI Jielin,ZHOU Keping,KE Bo.Association analysis of pore development characteristics and uniaxial compressive strength property of granite under freezing-thawing cycles[J].Journal of China Coal Society,2015,40(8):1783-1789.
[16] 曹文贵,王江营,翟友成,等.考虑残余强度影响的结构面与接触面剪切过程损伤模拟方法[J].土木工程学报,2012,45(4):127-134.
CAO Wengui,WANG Jiangying,ZHAI Youcheng,et al.Study of simulation method for the shear deformation of rock structural planes and interfaces with consideration of residual strength[J].China Civil Engineering Journal,2012,45(4):127-134.
[17] 李海潮,张升.基于修正Lemaitre应变等价性假设的岩石损伤模型[J].岩土力学,2017,38(5):1321-1326.
LI Haichao,ZHANG Sheng.A constitutive damage model of rock based on the assumption of modified Lemaitre strain equivalence hypothesis[J].Rock and Soil Mechanics,2017,38(5):1321-1326.
[18] 温韬,唐辉明,马俊伟,等.考虑初始损伤和残余强度的岩石变形过程模拟[J].地球科学,2019,44(2):652-663.
WEN Tao,TANG Huiming,MA Junwei,et al.Deformation simulation for rock in consideration of initial damage and residual strength[J].Earth Science,2019,44(2):652-663.
