旋流器以其操作简单,运行成本低,物理尺寸小等优点广泛应用于化工分离行业。比如,重介质旋流器因能提供远远大于重力场的分选力,有效降低分选下限,取得灰分相对比较低的细粒煤,成为重要的选煤设备[1]。旋流器内部流场对其分离性能起着关键作用。由于旋流器物料的不透光性及流场空间的狭小,其流场测量变得困难。近年来随着数值计算手段的逐步成熟以及高性能计算机的飞速发展,利用数值模拟来研究旋流器内部流场进而指导物料分离已经成为一种主流。然而,由于旋流器高变量梯度和强旋转特性的流场特征,尤其是使气-液两相出现明显界面特征的空气柱,使得准确模拟旋流器内部流场具有不确定性,有普适性的一些数学模型无法准确预测该旋流场,例如在湍流模型的选取上,梁政等人将 RSM湍流模型,k-ε湍流模型模拟得到的旋流器流场与实验结果作比,指出k-ε模型模拟得到的旋流器流场准确度较低[2],其中,k为湍流脉动动能;ε为湍流脉动动能的耗散率。SONALI Swain选择Standard k-ε,RSM湍流模型模拟低速运行下的小直径水力旋流器,并将两者模拟结果与实验数据对比,发现结果相近[3]。Irfan Karagoz对比Standard k-ε、RNG k-ε及RSM湍流模型预测的旋流器流场速度和湍流强度,发现后两者预测结果差异较小,因此基于内存和计算时间考量,笔者采用RNG k-ε模型进行后续计算[4]。除了湍流模型,其他数值计算方法如离散格式,压力-速度耦合方式的选择对模拟结果也会产生影响[5-6],文献几乎都只是简单地交代了选择结果,并没有给出理由及对比,见表1。
表1 文献中旋流器数值求解方法
Table 1 Numerical solution methods of references

作者湍流模型压力-速度耦合方式离散格式张悦刊[7]RSMSIMPLEFirst Order UpwindXU Yanxia[8]RSMSIMPLESecond Order UpwindKUANG S B[9]RSMSIMPLESecond Order UpwindHUANG Long[10]RSMCoupledQUICKJIN Jiang[11]RSMSIMPLECQUICKSWAIN Sonali[3]RSM/Standard k-εSIMPLEFirst Order UpwindVAKAMALLA T R[12]LES/RSM/DES/Standard k-ε/RNG k-ε未知QUICKAZADI M[13]RNG k-ε/RSMSIMPLECSecond Order UpwindJUENGCHAROENSUKYING J[14]RNG k-ε未知Second Order Upwind+First Order UpwindKARAGOZ Irfan[4]Standard k-ε/RNG k-ε/RSM未知未知
笔者将不同湍流模型、离散格式以及压力-速度耦合方式预测的旋流器内部流场中的切向速度和轴向速度与实验数据[15]进行对比及分析。同时,由于空气柱作为旋流器流场中必然且关键的存在,其形状尺寸受流场影响,反过来其形状尺寸也可以反映流场情况[16],所以也将其空气柱直径进行了对比,揭示其预测的流场情况,以期能给出适合求解旋流器流场的离散格式,压力-速度耦合方式以及湍流模型,为准确模拟旋流器内部流场提供更多的模拟参考。
1 旋流器内部流场数值模拟
1.1 几何模型
本文采用文献[15]提出的直径为75 mm的经典旋流器进行研究,结构尺寸如图1所示。
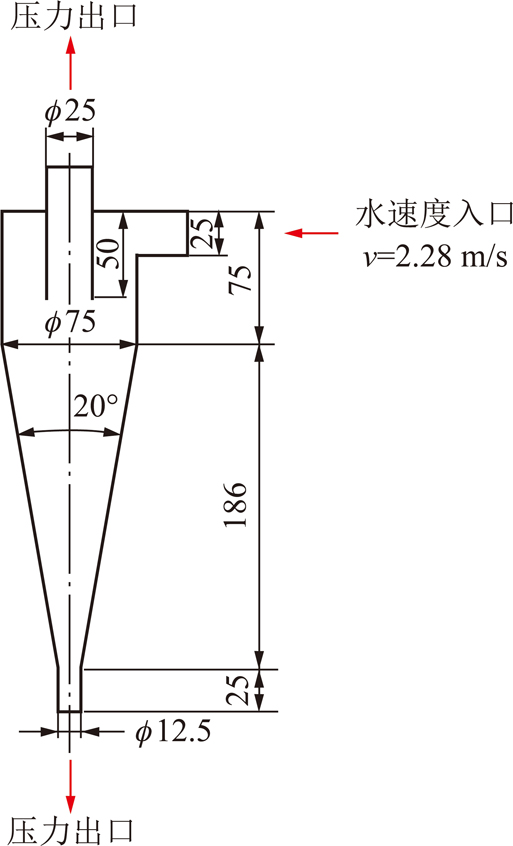
图1 φ75 mm旋流器结构示意
Fig.1 Schematic diagram of the 75 mm cyclone structure
1.2 网格划分与无关性检验
借助ICEM CFD软件对旋流器进行了六面体网格划分,如图2所示。选取了17 595,31 081,53 996三种网格进行网格无关性验证,模拟计算采用的基础模型见表2。图3为这3组网格在距离旋流器顶端60 mm处轴向速度与实验数据的对比图。由图3可知,31 081与网格数53 994的计算结果偏差在2%以内,与实验数据的吻合度较高且网格数量较少,故本文网格数目确定为31 081。
1.3 多相流模型与边界条件
采用VOF多相流模型来计算旋流器内液相与空气柱的交界面。旋流器在运行时底流口和溢流口会吸入空气,在流场中心形成空气柱,即:流场中气含率为100%的区域。因此主相为水,次相为空气。设置旋流器入口为流场的速度入口,大小依据文献[15]的实验条件设置为2.28 m/s,成分全为水。底流口和溢流口为压力出口,静压Ps=0与大气压相通。旋流器壁面设置成无滑移边界条件。采用非稳态计算,计算结果达到统计学稳定后,继续计算保存两个周期进行时均化处理,再导出所需数据作为最终计算结果。
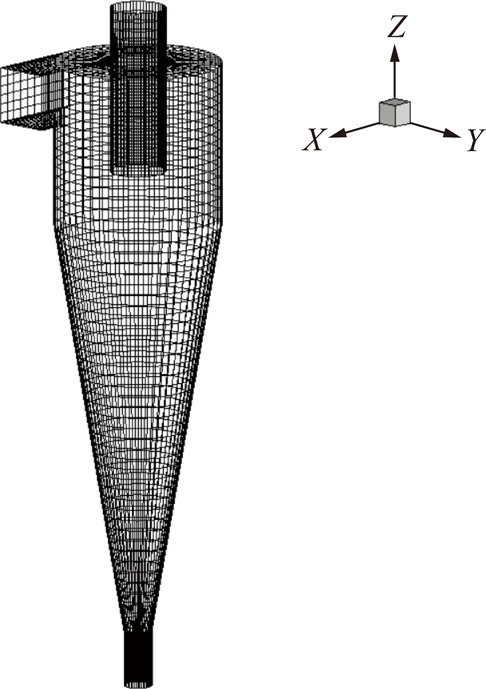
图2 75 mm旋流器网格划分
Fig.2 Grids partition in 75 mm cyclone
表2 基础模型
Table 2 Based model
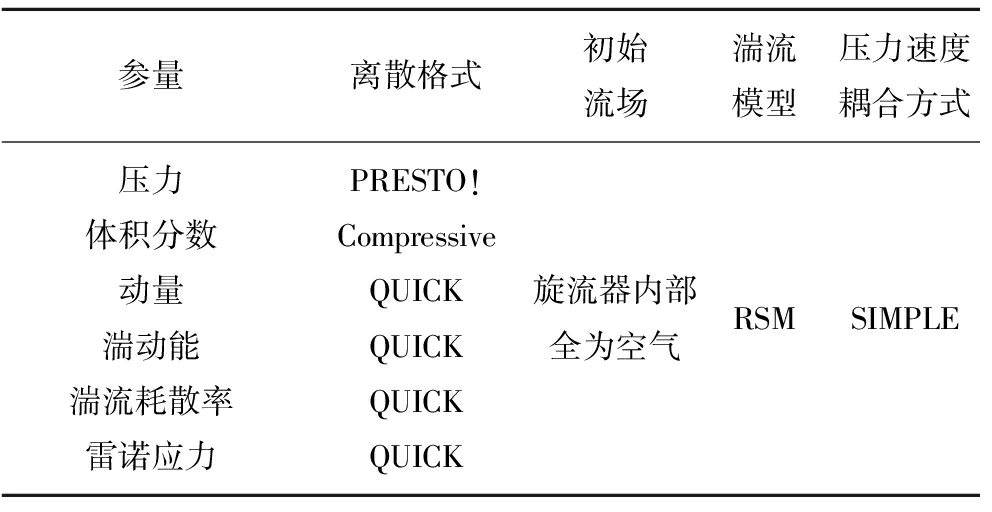
参量离散格式初始流场湍流模型压力速度耦合方式压力PRESTO!体积分数Compressive动量QUICK旋流器内部RSMSIMPLE湍动能QUICK全为空气湍流耗散率QUICK雷诺应力QUICK
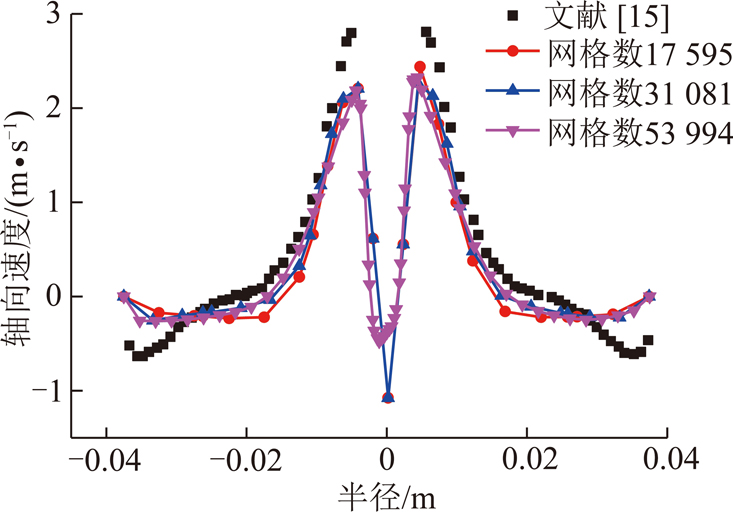
图3 网格无关性检验
Fig.3 Mesh independence test
1.4 基础模型
建立一个基础模型,后续研究在此模型基础上进行修改。
2 结果与讨论
2.1 湍流模型
RSM湍流模型摒弃了各向同性涡黏性假设,充分考虑了流线型弯曲、漩涡、和张力快速变化,能较好地预测各向异性湍流,理论上更适于模拟旋流场,其模型控制方程[16]为
Φij-εij+Rij+Sij+Dij
式中,Pij为应力项;Φij为源项;εij为黏性耗散项;Rij为旋转项;Sij,Dij为方程以柱坐标表达的曲线项;vt为湍流黏度;t为时间,u′为脉动速度;u为时均速度;i,j,k=1,2,3。
从文献[3-4,7-14]来看,Standard k-ε,Realizable k-ε以及RNG k-ε这几种湍流模型也常用来计算旋流场,控制方程见文献[16],在此不再赘述。文献一般只是选取了3种k-ε模型中的部分模型进行计算,没有系统地将3者进行比较。因此,本文分别采用RSM,Standard k-ε,Realizable k-ε以及RNG k-ε四种湍流模型来预测旋流器的内部流场。4种湍流模型近壁面都采用标准壁面函数,方程见文献[17]。在导入Fluent进行模拟计算时设置了y+网格自适应,满足湍流模型对壁面网格的要求。在表2所示的基础模型上,保持其他设置不变,仅修改湍流模型,针对计算结果讨论不同湍流模型对预测结果的影响。
借助文献[15]中已有的实验数据,即距离旋流器顶端60 mm处的切向、轴向速度,与模拟结果进行对比,如图4所示。由图4可知,RSM模型除了在空气柱附近对切向及轴向速度峰值预测偏低之外,其余部分吻合度均较好,准确预测出了呈M型分布的切向速度,即成功捕捉到流体的Rankine涡特性,该预测结果与文献结论一致[2,18]。其余3种k-ε模型预测效果皆不理想,速度出现较大偏差,相比较而言RNG k-ε模型的误差略低于其他2种。分析其原因是这3种k-ε模型都是建立在各向同性涡黏性假设基础之上,不适合求解旋流器这种强旋流的各向异性流动。包括进行过旋流修正的RNG k-ε和Realizable k-ε模型,仍然难以预测到旋流器内部高变量梯度和强旋转特性的流场特征。而RSM模型则彻底抛弃了各向同性涡黏性假设,考虑了流线型弯曲、漩涡、旋转和张力快速变化,故对复杂流动有更高精度的预测潜力[19]。
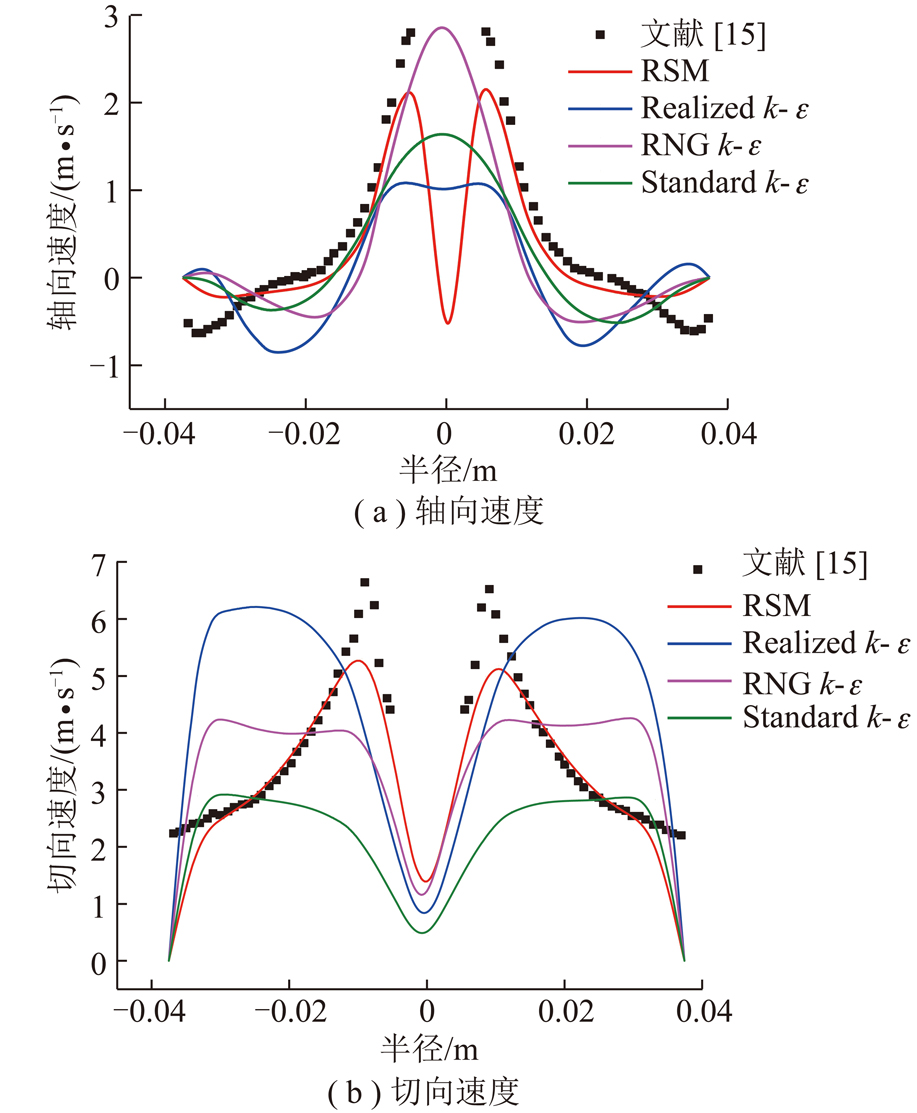
图4 不同湍流模型预测速度与文献实验数据对比
Fig.4 Comparison of predicted velocities and measured data between different turbulent models
图5为4种湍流模型预测的液相体积分数云图,蓝色部分代表空气柱。由图5可知,RSM完整预测了流场中的空气柱,RNG k-ε预测出了部分空气柱,Realizable k-ε在溢流口处有微弱进气,Standard k-ε则完全没有进气现象。说明RSM湍流模型在预测空气柱上具有优势,结论与文献[20]一致,3种k-ε模型预测效果皆不理想。RNG k-ε比其他2种k-ε模型预测旋流时误差稍低,但仍旧不适合用于模拟旋流问题。因为RNG k-ε湍流模型虽然考虑了漩涡对湍流的影响,即湍流的各向异性效应,但是并没有突破涡黏性假设下的各向同性的框架,尤其只能部分模拟出流场中的空气柱便可见一斑。
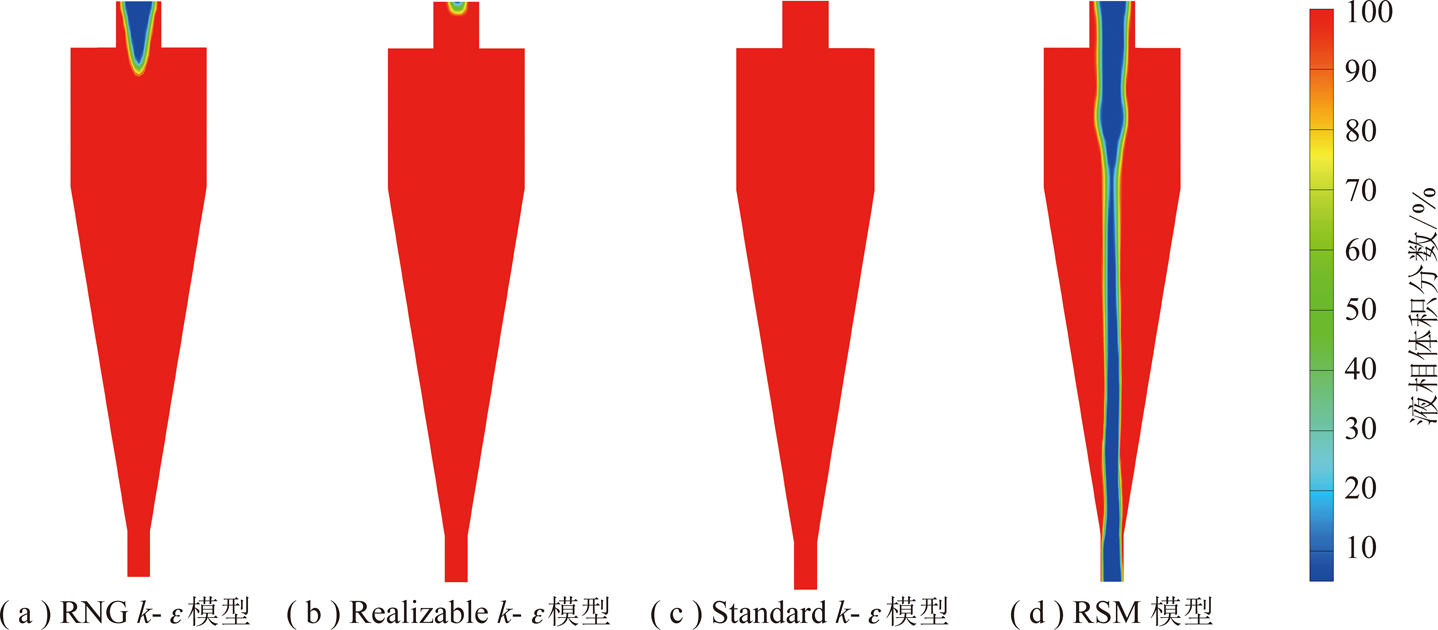
图5 不同湍流模型预测的液相体积分数云图
Fig.5 Results of simulating the internal air core in cyclone at different k-ε models
2.2 离散格式
在有限体积法中,离散格式指的是控制体积边界的取值方式。First Order Upwind格式,对于来流从上游流向下游的情况,上游控制体积的节点参数对边界的影响大于下游控制体积的节点参数,所以边界取值取上游的节点参数值。Second Order Upwind是利用上游最近的一个节点和另一个上游的节点值来取得边界值。QUICK格式通过提高界面上插值函数的阶数来提高格式的截断误差,常用于四边形或六面体网格。Third-order MUSCL,3阶离散格式,主要用于非结构网格,预测二次流,漩涡等精度较高。Power Law格式精度与First Order Upwind格式精度基本持平。这5种离散格式的计算公式见文献[21]。
在表2所示的基础模型上,保持其他设置不变,采用Third-order MUSCL,Power Law,First Order Upwind,QUICK以及Second Order Upwind五种格式离散动量、湍动能、湍流耗散率以及雷诺应力,求解得到的液相体积分数云图,如图6所示,蓝色部分代表空气柱。由图6可知,前3种离散格式没有成功求解出流场中完整的空气柱,说明其预测的流场环境与实际流场存在较大差异。QUICK与Second Order Upwind离散格式成功计算出了流场中完整的空气柱,再将二者在不同高度处预测的空气柱直径进行对比,如图7所示。
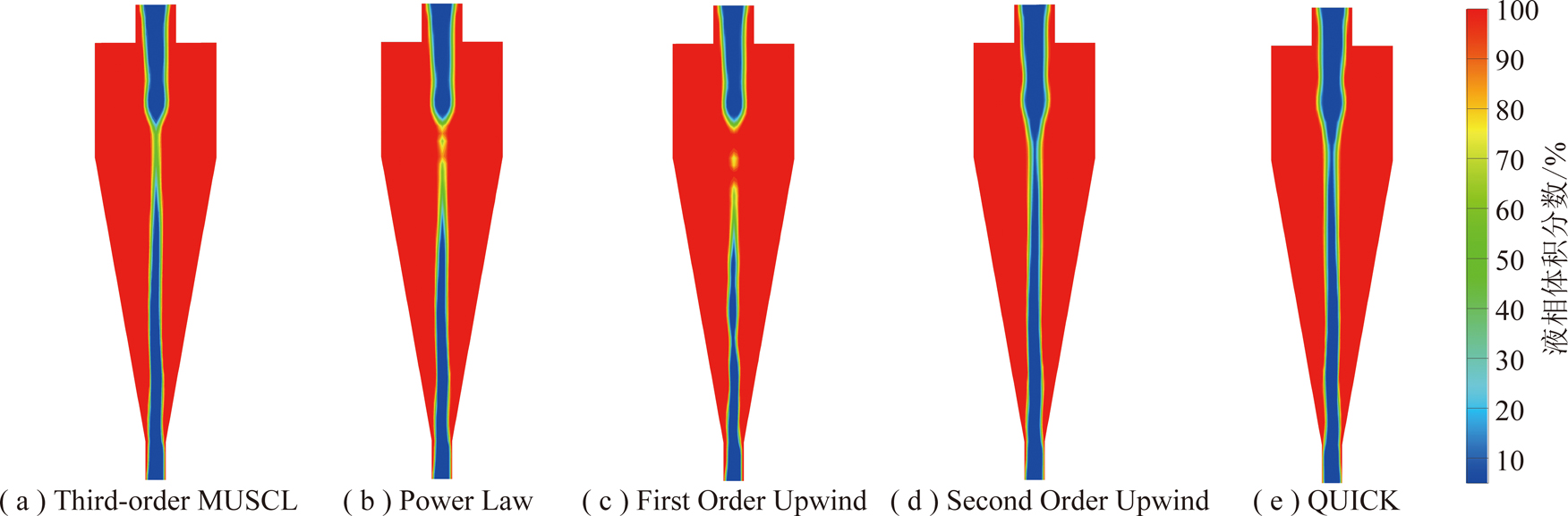
图6 不同离散格式求解的液相体积分数云图
Fig.6 Results of simulating the internal air core in cyclone at different discrete formats
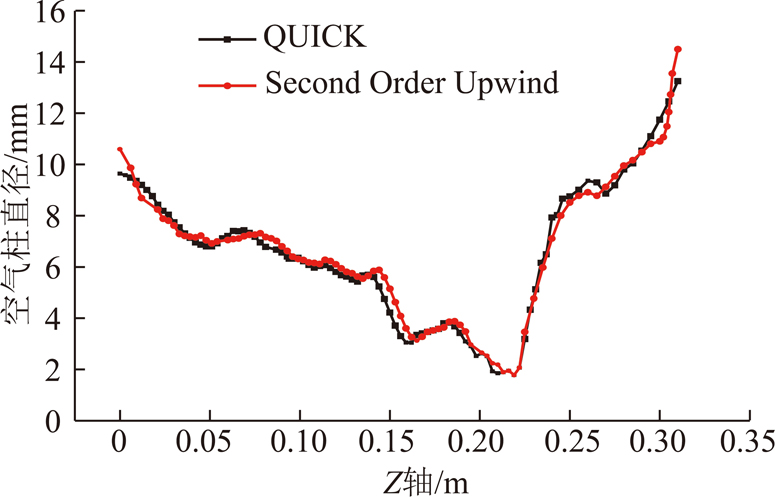
图7 不同离散格式下的空气柱直径随高度的变化
Fig.7 Diameter of air core varied with height at different discrete formats
由图7可知,二者预测的空气柱直径相近,没有明显差异。由此推断其预测的流场环境也应该相似。与此同时,将QUICK,Second Order Upwind在距离旋流器顶端60 mm和120 mm处的轴向、切向速度与实验数据进行对比,如图8所示。经过对比可以得知,二者切向速度曲线基本重合,如图8(a),8(c)所示。由图8(b),8(c)可知,Second Order Upwind预测的轴向速度与QUICK格式相比在空气柱附近速度偏差达到最大,相差0.095 m/s,差异较小。且二者预测的空气柱直径相近,没有明显差异,可以认为对于本文所研究对象及研究范围,QUICK,Second Order Upwind离散格式差别不大。
2.3 压力-速度耦合方式
SIMPLE,SIMPLEC,PISO,Coupled都是用来求解速度和压力耦合的算法。SIMPLE算法使用压力和速度之间的相互校正关系来强制质量守恒并获取压力场。在SIMPLE算法的基础上发展了SIMPLEC算法,SIMPLEC算法在收敛策略上较之SIMPLE有所改进,但并无本质区别,故本文不对SIMPLEC算法进行研究。PISO算法执行了2个附加校正:相邻校正和偏斜校正,避免了SIMPLE和SIMPLEC两种算法在压力校正方程解后,新的速度值和响应流量不满足动量平衡,需要重复计算直至平衡的问题。
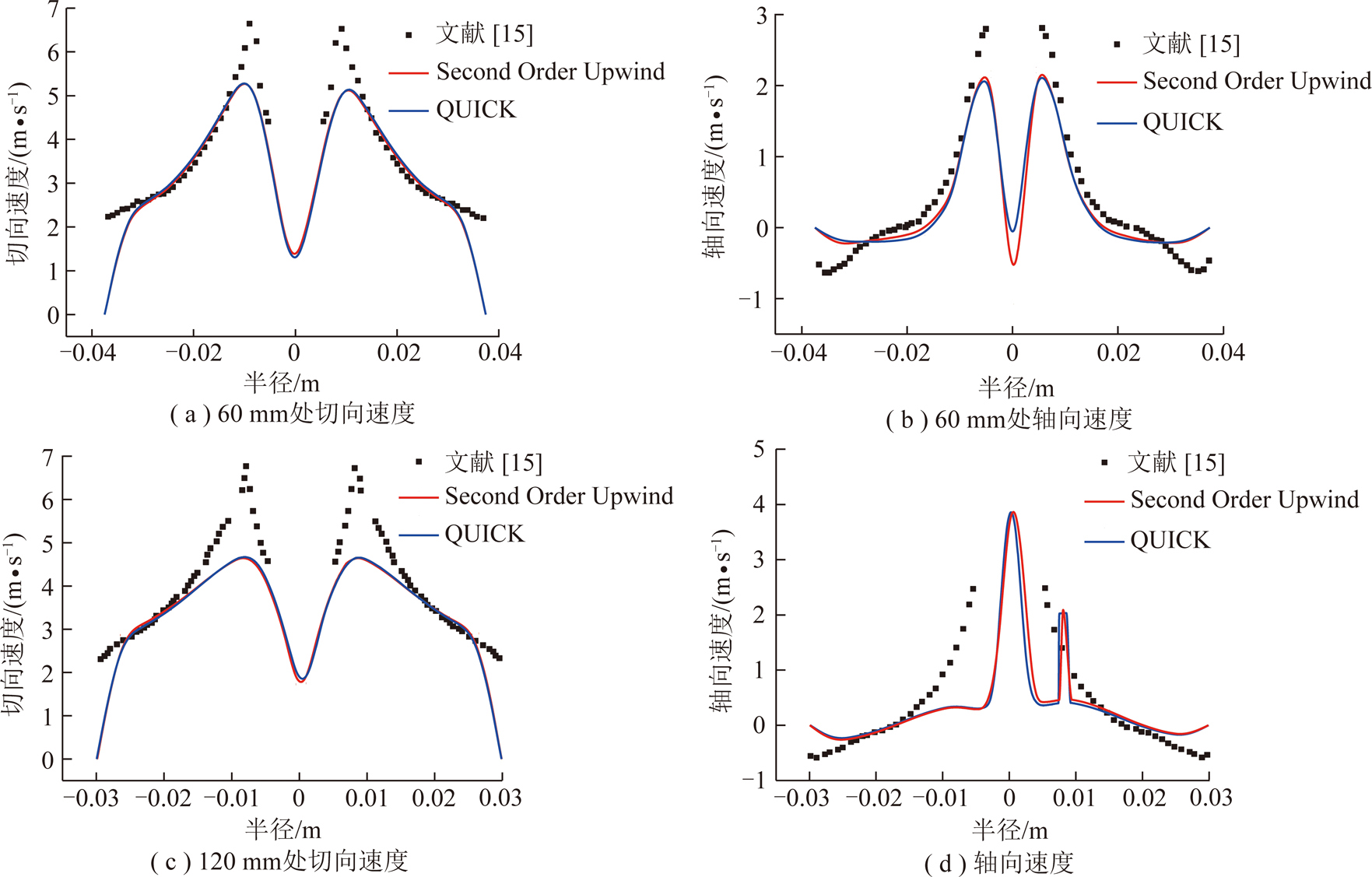
图8 不同离散格式下距离旋流器顶端不同高度处平面速度与文献实验数据对比
Fig.8 Comparison between experimental and simulated results at the different discrete formats and locations from the top wall
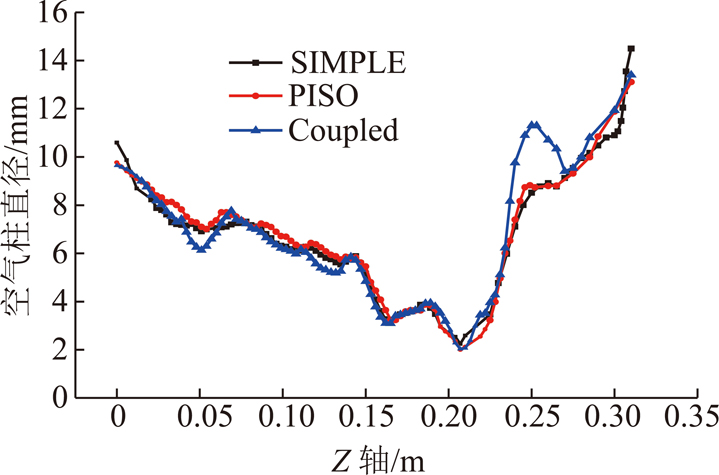
图9 不同压力-速度耦合方式下的空气柱直径随高度的变化
Fig.9 Diameter of air core varied with height at different pressure-velocity coupling modes
在表2所示的基础模型上,只改变压力-速度耦合方式。图9为SIMPLE,PISO,Coupled三种压力-速度耦合方式在不同高度处预测的空气柱直径对比。由图9可知,SIMPLE,PISO算法求解出的空气柱直径相近。Coupled算法在42~60 mm高度处(锥段)求解得到的空气柱直径偏小。与SIMPLE算法相比,直径最大相差0.78 mm;与PISO算法相比,直径最大相差0.97 mm。在234~270 mm高度处(溢流管段),空气柱尺寸偏大。与SIMPLE算法相比,直径最大相差2.57 mm;与PISO算法相比,直径相差最大为2.52 mm。在42~60 mm 段,取47,55 mm两个高度上的速度进行对比,如图10(a),10(b)所示;在234~270 mm段,取245,260 mm两个高度进行对比,如图10(c),10(d)所示。由图10可知,Coupled算法求解出的空气柱直径偏小的区域,速度偏大;空气柱直径偏大的区域,速度偏小。速度愈大,流场环境愈复杂,愈不利于空气柱的形成与稳定。
图11为SIMPLE,PISO,Coupled算法在距离旋流器顶端60 mm与120 mm处模拟得到的切向、轴向速度与文献实验数据的对比图。由图11(c),11(d)可知,SIMPLE算法在空气柱附近预测的速度与实验数据的吻合度高于PISO,Coupled算法。切向速度比PISO,Coupled算法最多高0.15 m/s;轴向速度比PISO算法最多高0.164 m/s,比Coupled算法最多高 0.16 m/s。由此可以看出SIMPLE算法的主要优势体现在对空气柱附近流体区域的速度预测精度高。观察图11(b)的轴向速度分布可知,Coupled算法在空气柱附近预测的轴向速度偏低。因此,可以认为SIMPLE算法是较为适合计算旋流器流场的压力-速度耦合方法。
3 结 论
(1)RSM湍流模型可以较为准确地预测旋流器流场,仅在空气柱附近区域预测的速度值偏低。RNG k-ε、Realizable k-ε以及Standard k-ε湍流模型预测的该流场与实际流场存在较大偏差,其中RNG k-ε模型误差较Realizable k-ε以及Standard k-ε模型稍低。
(2)SIMPLE,PISO及Coupled三种压力-速度耦合方式对计算结果的影响不大,相比较而言,SIMPLE算法为较适合计算旋流器流场的压力-速度耦合方式。Couple较其他2种算法在溢流管段预测的空气柱直径偏大,速度偏小,部分锥段空气柱直径偏小,速度偏大。
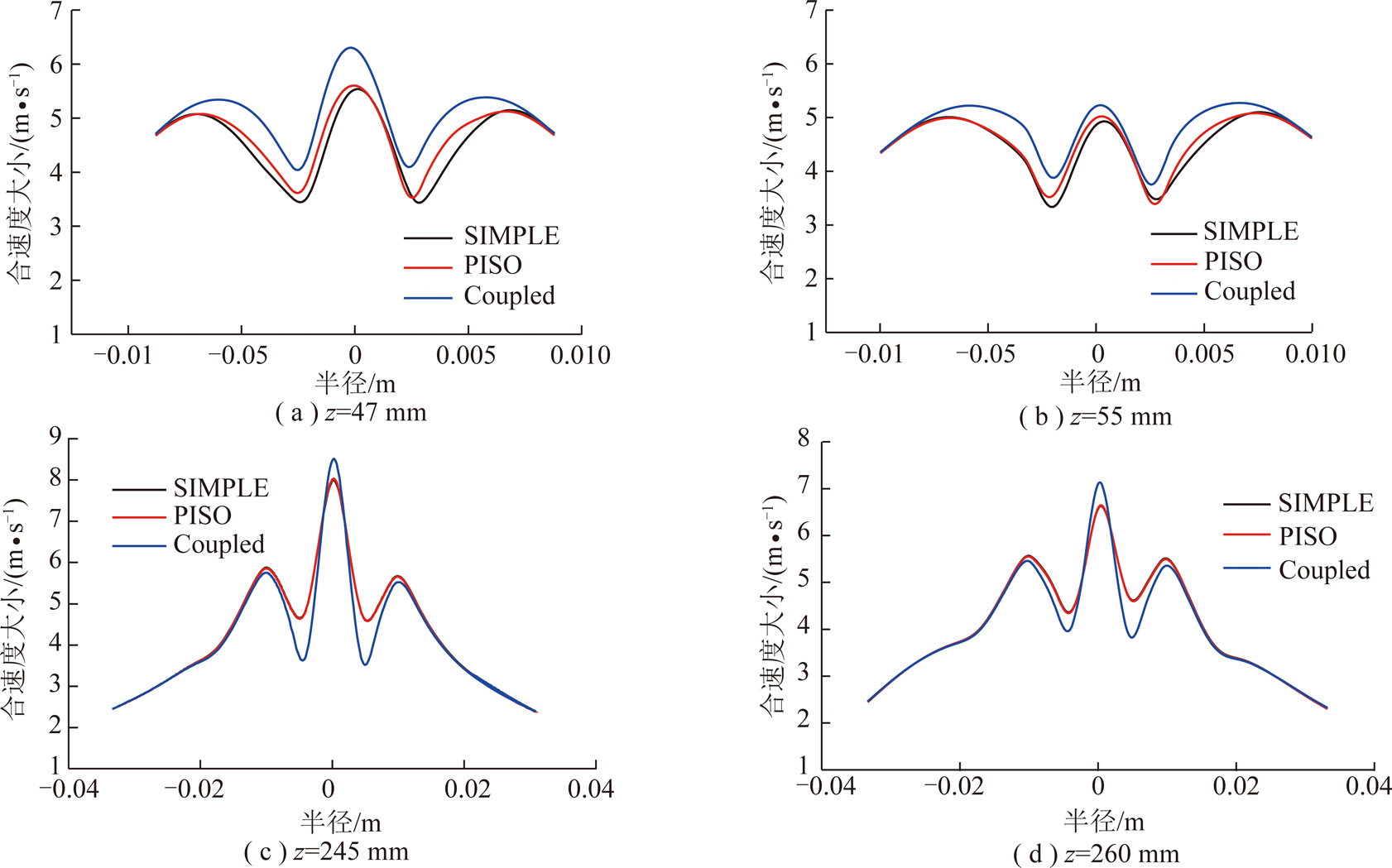
图10 不同高度处速度大小对比
Fig.10 Velocity comparison at different heights
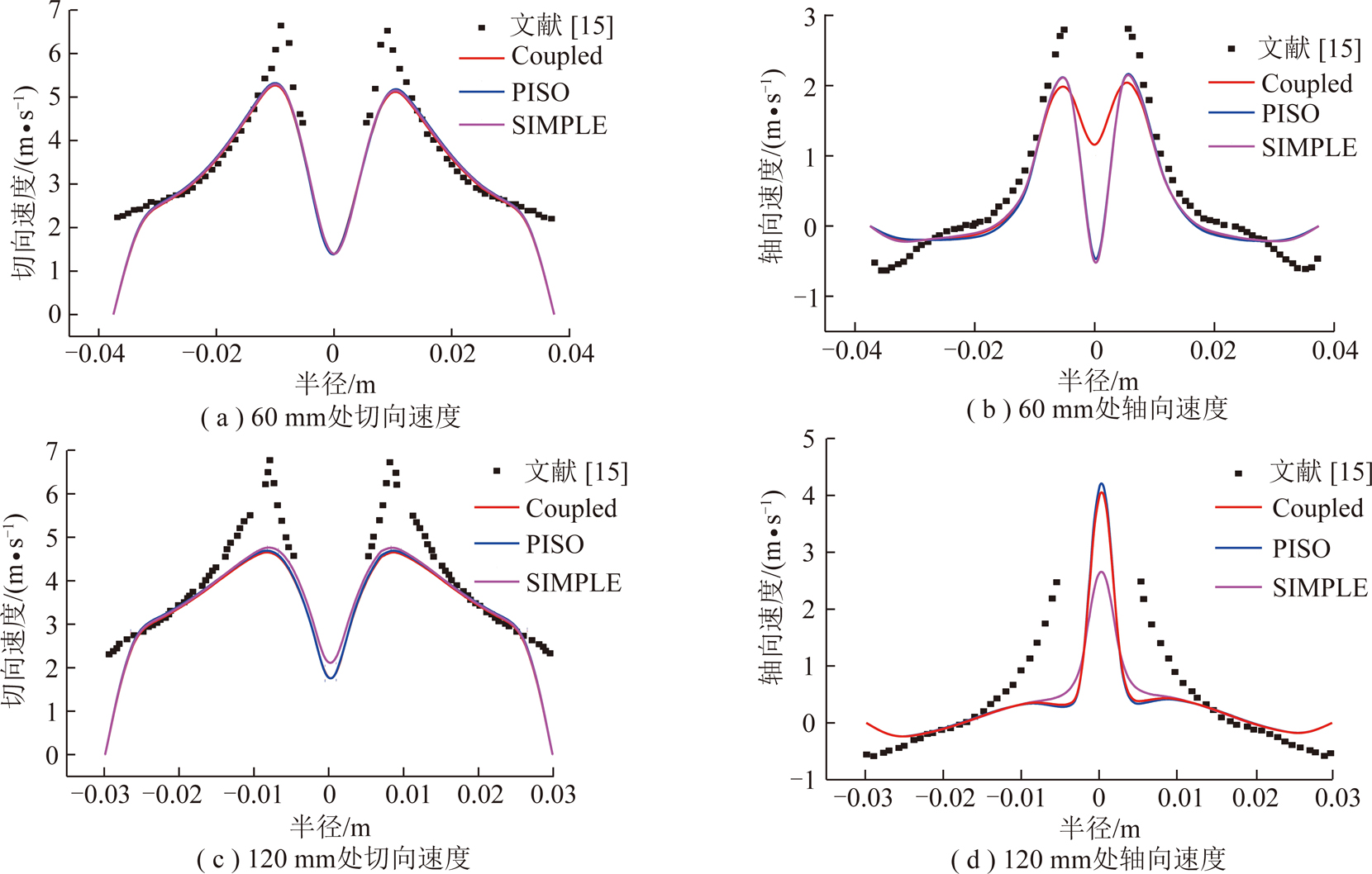
图11 不同压力-速度耦合方式下距离旋流器顶端不同高度处平面速度与文献实验数据对比
Fig.11 Comparison between experimental and simulated results at the different pressure-velocity coupling modes and locations from the top wall
(3)QUICK与Second Order Upwind离散格式在预测旋流器内部流场时差别不大。Third-order MUSCL,Power Law,First Order Upwind离散格式未能算出流场中完整的空气柱。
[1] 王冲.试论选煤设备的应用前景分析[J].化工管理,2018,489(18):50.
WANG Chong.Application prospect analysis of coal preparation equipment[J].Chemical Management,2018,489(18):50.
[2] 梁政,吴世辉,任连城.论水力旋流器流场数值模拟中湍流模型的选择[J].天然气工业,2007,27(3):119-121.
LIANG Zheng,WU Shihui,REN Liancheng.The selection of turbulent model in numerical simulation of flow field of hydraulic cyclone[J].Natural Gas Industry,2007,27(3):119-121.
[3] SWAIN S,MOHANTY S.A 3-dimensional Eulerian-Eulerian CFD simulation of a hydrocyclone[J].Applied Mathematical Modelling,2013,37(5):2921-2932.
[4] KARAGOZ I,KAYA F.CFD investigation of the flow and heat transfer characteristics in a tangential inlet cyclone[J].International Communications in Heat & Mass Transfer,2007,34(9-10):1119-1126.
[5] 胡洪,黄虎,宋倩倩,等.不同对流项离散格式对流场计算的影响[J].数值计算与计算机应用,2010,31(2):153-160.
HU Hong,HUANG Hu,SONG Qianqian,et al.The influence of different discrete scheme of the convective term on fluid field calculation[J].Journal On Numerical Methods and Computer Applications,2010,31(2):153-160.
[6] 王明波,王瑞和.不同离散格式在湍流旋流流动数值模拟中的应用[J].中国机械工程,2007,18(5):600-603.
WANG Mingbo,WANG Ruihe.Application of different discretization schemes to the numerical simulation of swirling turbulent flow[J].China Mechanical Engineering,2007,18(5):600-603.
[7] 张悦刊,刘培坤,杨兴华,等.基于CFD的泥浆净化旋流器湍流流场数值模拟[J].流体机械,2014,(6):26-32.
ZHANG Yuekan,LIU Peikun,YANG Xinghua,et al.Numerical simulation of turbulent flow field of mud hydrocyclone based on CFD[J].Fluid Machinery,2014,(6):26-32.
[8] XU Y,SONG X,SUN Z,et al.Steady-state distribution of air-core in a hydrocyclone[J].Canadian Journal of Chemical Engineering,2017,95(4):757-766.
[9] KUANG S B,CHU K W,YU A B,et al.Numerical study of liquid-gas-solid flow in classifying hydrocyclones:Effect of feed solids concentration[J].Minerals Engineering,2012,31:17-31.
[10] HUANG L,DENG S,GUAN J,et al.Development of a novel high-efficiency dynamic hydrocyclone for oil-water separation[J].Chemical Engineering Research & Design,2018,130:266-273.
[11] JIANG J,YING R,FENG J,et al.Computational and experimental study of the effect of operating parameters on classification performance of compound hydrocyclone[J].Mathematical Problems in Engineering,2018,2018:1-16.
[12] VAKAMALLA T R,MANGADODDY N.Numerical simulation of industrial hydrocyclones performance:Role of turbulence modelling[J].Separation & Purification Technology,2017,176,23-29.
[13] AZADI M,MOHEBBI A.A CFD study of the effect of cyclone size on its performance parameters[J].Journal of Hazardous Materials,2010,182(1-3):835-841.
[14] JUENGCHAROENSUKYING J,POOCHINDA K,CHALERMSINSUWAN B.Effect of cyclone vortex finder and inlet angle on solid separation using CFD simulation[J].Energy Procedia,2017,138:1116-1121.
[15] HSIEH K T,RAJAMANI K.Phenomenological model of the hydrocyclone:Model development and verification for single-phase flow[J].International Journal of Mineral Processing,1988,22:223-237.
[16] HARARAH M A,ENDRES E,DUECK J,et al.Flow conditions in the air core of the hydrocyclone[J].Minerals Engineering,2010,23:295-300.
[17] 刘峰,邵涛.重介质旋流器壁面处理对湍流数值模拟的影响[J].煤炭学报,2008,33(9):1035-1039.
LIU Feng,SHAO Tao.Effect of the wall treatment made to the heavymedium cyclone on numerical simulation of the turbulent flow[J].Journal of China Coal Society,2008,33(9):1035-1039.
[18] 刘峰,钱爱军,郭秀军.重介质旋流器流场湍流数值计算模型的选择[J].煤炭学报,2006,31(3):346-350.
LIU Feng,QIAN Aijun,GUO Xiujun.Selection of numerical computational models of the turbulence flows in heavymedium cyclone flow field[J].Journal of China Coal Society,2006,31(3):346-350.
[19] 马艺,王振波,金有海.不同湍流模型和差分格式对旋流器流场的影响[J].化工机械,2009,36(6):596-599.
MA Yi,WANG Zhenbo,JIN Youhai.Influence of different turbulence current models and different schemes on the flow field of hydrocyclone[J].Chemical Machinery,2009,36(6):596-599.
[20] 梁绍青,王铖健.旋风分离器流场数值模拟及其涡结构识别[J].煤炭学报,2014,39(S1):262-266.
LIANG Shaoqing,WANG Chengjian.Numerical simulation of the flow field in a cyclone separator and vortex identification[J].Journal of China Society,2014,39(S1):262-266.
[21] 陶文铨.数值传热学-第2版[M].西安:西安交通大学出版社,2001.
