潮湿细粒煤炭的深度干法筛分是当今煤炭行业亟需解决的难题[1-2]。深度筛分时,由于煤炭在开采过程中,煤层中的渗水、防尘的喷水以及黏性矿物的存在,导致颗粒小、比表面积大的煤粒互相黏连而团聚板结,造成筛面堵孔严重的现象,普通振动筛很难完成潮湿细粒煤炭深度筛分的任务,严重制约了煤炭深度加工行业的发展[3-4]。振动弛张筛以其筛面加速度大、筛分效率高、不易堵孔和适用性强等特点得到了广泛的应用和发展[5-7]。为了达到理想的筛分效果,振动弛张筛的动力学分析受到了学者们的广泛关注。
XIONG和陈志强等学者假设振动弛张筛为线性系统,分析了其动力学响应,解释了弛张筛的振动机理以及合理的工作区域[8-10],该线性模型虽被广泛使用,但不能准确描述剪切弹簧的振幅相关性和频率相关性,故在分析振动弛张筛动力学响应时采用该模型存在较大的误差;翟宏新从双质体非线性角度理论分析了弛张筛的振动机理,指出了剪切弹簧的非线性特性对于系统的动力学响应有着重要影响[11],但该研究仅为理论假设,剪切弹簧的真实动态特性并未得到合理的解释。作为传递主筛框和浮动筛框(简称主浮筛框)之间振动的重要部件,剪切弹簧的动态特性直接影响着主浮筛框以及弹性筛面的运动,进而影响筛面上物料的运动规律,其对系统的筛分效果具有重要的影响[12-13]。但在上述研究中对于振动弛张筛系统中剪切弹簧的模型仅为理论研究,其真实的动态特性并未得到深入研究,以至于振动弛张筛的动力学响应不能被准确的描述。
目前,有关橡胶弹簧动态特性的研究主要包括两个方面:频率相关性和振幅相关性。在描述橡胶弹簧频率相关性时,最广泛使用的模型为Kevin-Voigt模型[14],其由线性弹簧和阻尼器并联而成,在研究弛张筛动力学响应时,该模型也被广泛用来描述剪切弹簧的动态特性,但该模型过高的预测高频时阻尼的大小,且不能准确描述弹簧的振幅相关性[15-16];将线性弹簧和阻尼器串联可形成Maxwell模型,其可较好的描述高频时弹簧的动态刚度,但过低的预测高频时弹簧的动态阻尼[17];为了更好的描述橡胶弹簧动态特性的频率相关性,SJÖBERG,SEDLACZEK和ZHU等采用分数导数模型来描述弹簧的黏性力,并利用实验结果验证了该模型的优越性[18-20]。在描述橡胶弹簧动态特性振幅相关性时,BERG提出了光滑的摩擦模型,与黏滑摩擦模型相比,该模型能更好的吻合橡胶弹簧的迟滞环曲线,并被广泛使用[21-22],但其过低的预测激振振幅较小时弹簧的动态刚度和阻尼。
针对上述研究的不足,笔者提出一种新的橡胶弹簧模型来描述剪切弹簧的动态特性,该模型不仅包含弹性元件,还包含摩擦元件和黏性元件。弹性元件由非线性弹簧表示,描述剪切弹簧静态非线性弹性;摩擦元件由优化后的Berg摩擦模型表示,表征剪切弹簧动态特性的振幅相关性;黏性元件由分数导数模型表示,描述剪切弹簧动态特性的频率相关性。随后用剪切弹簧动态测试实验结果来验证该模型的准确性,将该非线性剪切弹簧模型嵌入振动弛张筛动力学系统中,利用Newmark算法对该系统的动力学响应进行计算,并分析了新振动弛张筛动力学模型在不同系统参数条件下的动力学响应。
1 剪切弹簧动态特性实验及分析
橡胶剪切弹簧(长×宽×高:203 mm×70 mm×48 mm)的动态特性是在Instron E10000型动力学实验平台(精确度±0.5%)上进行测试的,如图1所示。该剪切弹簧上部与设备驱动系统连接,下部安装在力传感器(精确度±0.005%)上部。测试过程中,通过Instron测试软件输入正弦激励信号的振幅和频率,测试开始后,系统记录相应的力信号。为了尽可能消除温度因素对弹簧动态特性的影响,每两次测试中间需要间隔几分钟,并利用热像仪(精确度±2%)来保证弹簧每次测量的起始温度恒为23 ℃。此处需要注意的是弹簧在每次测试过程中虽然保证了起始温度条件一致,但由于弹簧内部摩擦力的作用,弹簧在测试的过程中,内部温度会升高,对实验结果会造成微小的影响。

图1 橡胶剪切弹簧动态测试实验
Fig.1 Dynamic test of rubber shear spring
剪切弹簧的动态特性可用动刚度K和滞后角θ(表征阻尼)[17]来表示
![]()
(1)
θ=arcsin D
(2)
式中,![]() 和Fmin,i分别为每个迟滞环曲线的最大和最小力;xmax,i和xmin,i分别为最大和最小位移;Ei为迟滞环曲线的面积;n为所取迟滞环的个数。
和Fmin,i分别为每个迟滞环曲线的最大和最小力;xmax,i和xmin,i分别为最大和最小位移;Ei为迟滞环曲线的面积;n为所取迟滞环的个数。
1.1 力-位移曲线
由于剪切弹簧中阻尼的存在,剪切弹簧在简谐力循环往复的作用下力与位移曲线形成迟滞环。由式(1),(2)可知,迟滞环曲线中最大和最小力之间连线的斜率(即迟滞环的整体斜率)可用来表征动刚度,迟滞环曲线面积的大小即为能耗,可反映滞后角的大小。为了研究激振振幅对剪切弹簧动态特性的影响,取激振频率为0.01 Hz,来消除黏性力的影响[20,23-24],实验测得不同激振振幅条件下剪切弹簧的迟滞环曲线,如图2(a)所示,随着振幅的增加,迟滞环整体顺时针转动,使得其整体斜率减小,即剪切弹簧动刚度减小;当激振振幅一定时(6 mm),实验测得不同激振频率时剪切弹簧的迟滞环曲线,如图2(b)所示,随着频率的增加,迟滞环整体逆时针转动,使得其整体斜率增大,即剪切弹簧动刚度增大。由于所研究剪切弹簧的阻尼较小,不同条件下,剪切弹簧迟滞曲线面积的变化规律不易直接观察,但可利用式(2)计算剪切弹簧滞后角来分析不同条件下剪切弹簧阻尼的变化规律,详见1.2节。
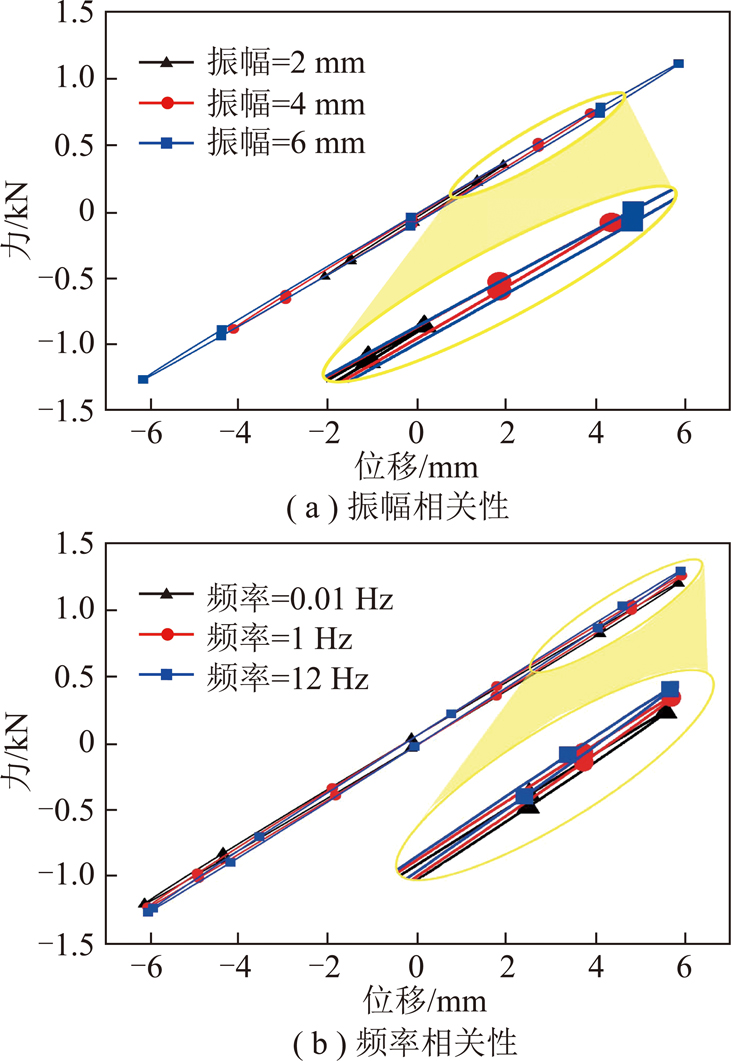
图2 剪切弹簧迟滞环曲线
Fig.2 Hysteresis loops of shear spring
1.2 动刚度和滞后角
分别取激振振幅为3.5,4.0和4.5 mm,频率为1~6 Hz,实测得到剪切弹簧的动态特性与激振振幅和频率的相关性,如图3所示,当激振振幅不变,频率增加时,动刚度增加,滞后角总体呈现增加趋势。当激励频率不变,振幅增加时,动刚度减小,滞后角略微减小。实验结果表明:剪切弹簧的动态特性具有振幅相关性和频率相关性。
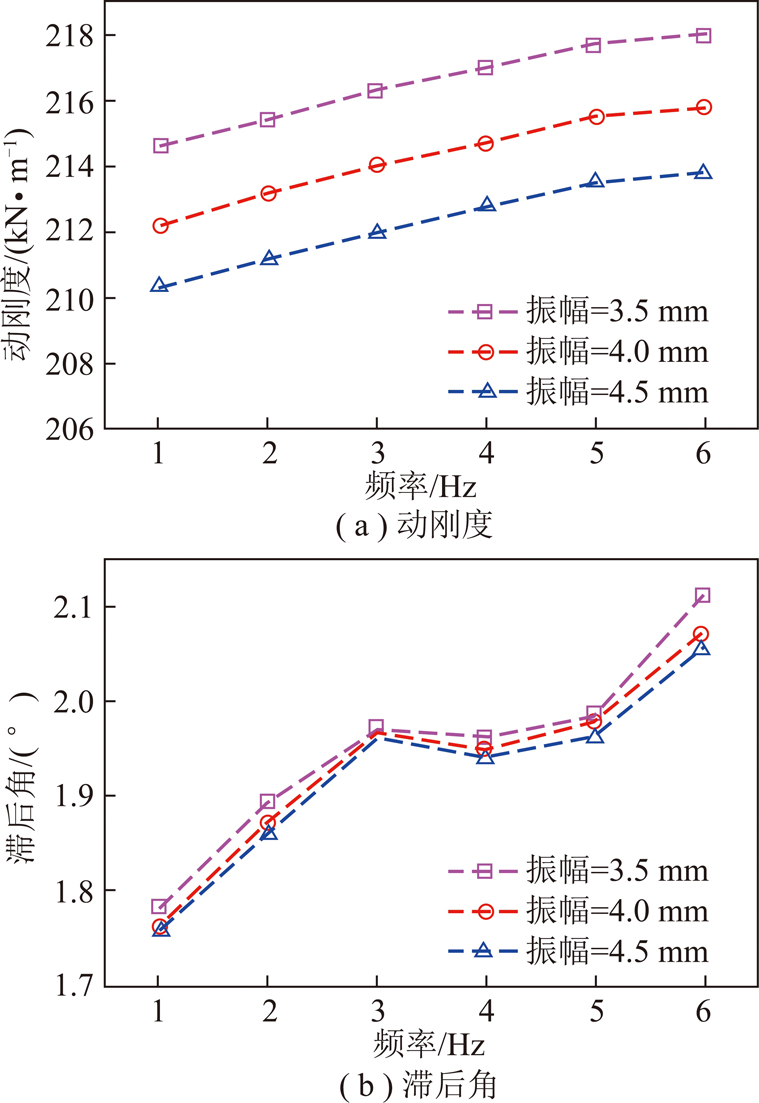
图3 剪切弹簧动态特性
Fig.3 Dynamic characteristics of shear spring
2 剪切弹簧动态特性非线性建模
根据剪切弹簧动态特性实验测试结果可知,在建立剪切弹簧动态模型时,须考虑其动态特性的振幅相关性和频率相关性。本文建立了基于弹性、摩擦和分数导数模型的剪切弹簧非线性模型,如图4所示。该模型力和位移的关系包括3个部分:弹性力由非线性弹簧模型表示,描述剪切弹簧的静态非线性特性;摩擦力由优化后的Berg模型来表示,描述剪切弹簧动态特性的振幅相关性;黏性力由分数导数模型来表示,描述剪切弹簧动态特性的频率相关性。因此,剪切弹簧变形产生的总力F为非线性弹性力Fe、摩擦力Ff和黏性力Fv三者的和。
F=Fe+Ff+Fv
(3)
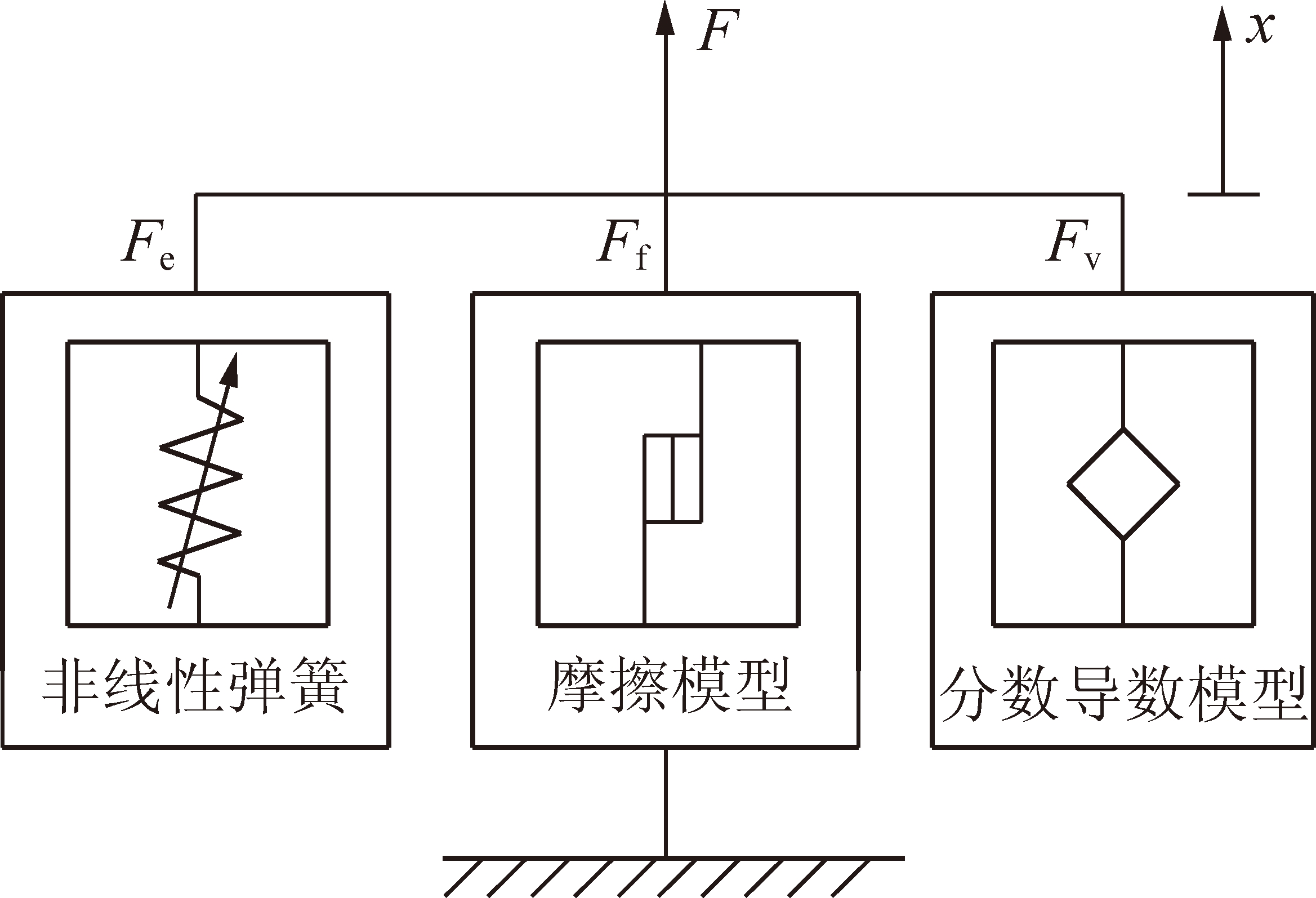
图4 剪切弹簧非线性动态模型
Fig.4 Nonlinear dynamic model of shear spring
2.1 弹性恢复力
当剪切弹簧变形量增加时,弹性力Fe呈现出非线性,其与激振位移x=x0sin(ωt)的关系可表示为
Fe=Kex
(4)
式中,ω和t分别为激振角速度和时间;弹性刚度Ke=Ke(x0)为有关激振振幅x0的函数。
2.2 摩擦力
经典的Berg摩擦模型过低的预测激振振幅较小时橡胶弹簧动态特性,此处通过优化Berg摩擦模型来描述剪切弹簧动态特性的振幅相关性,摩擦力可表示为
当x=xs:
Ff=Ffs
(5)
当x>xs:
![]()
(6)
当x<xs:
![]()
(7)
其中,xs和Ffs分别为位移和力的参考点,该参考点可计算当前时刻的摩擦力,计算过程中,由于摩擦力的方向不断发生变化,因此需要不断实时更新参考点,瞬时摩擦因数ε=Ffs/Ffmax,最大摩擦力Ffmax=Ffmax(x0)和摩擦力方向变化产生的过度位移a2=a2(x0)都为有关激振振幅x0的函数。
2.3 黏性力
剪切弹簧的黏性力由分数导数模型来表示,力与位移的关系可表示为
![]()
(8)
式中,b为该黏性力的系数;t为时间;α为分数导数阶数,α∈(0,1);当α=0和α=1时,该模型可分别表示线性弹簧和阻尼器,表明该模型随着α的增加,阻尼力增大。
利用Riemann-Liouville型分数阶导数定义,式(8)可转化为
![]()
(9)
式中,Gamma函数可定义为
Γ(n)=![]() tn-texp(-t)dt
tn-texp(-t)dt
利用Grünwald-Letnikov定义可得到黏性力在时域上的求解:
![]()
(10)
式中,Δt为时间积分步长;xn为tn=nΔt时弹性元件的变形量;j∈[0,n-1]为第j个时间积分步长;xn-j为tn-j瞬时弹性元件的形变;tn为n个时间步长的时间;τ为积分公式里面的一个变量,范围为(α,t)。
2.4 模型参数的确定
由式(4)~(7)和(10)可知,在该剪切弹簧非线性模型中,影响其动态特性的相关参数为:Ke,Ffmax,a2,α和b。其中Ke,Ffmax和a2可通过准静态(激振频率0.01 Hz)实验得到的迟滞环曲线获得,如图5所示,之后将不同振幅条件下的Ke,Ffmax 和a2数据拟合即可得到模型参数与振幅的关系表达式:Ke=Ke(x0),Ffmax=Ffmax(x0)和a2=a2(x0)。最后,实验测得不同频率下剪切弹簧的迟滞曲线,应用最小二乘法,可确定模型参数α和b,具体方法可参照文献[17]。表1为所研究的剪切弹簧的力—位移迟滞环曲线测试结果得到的非线性模型参数的相关数值。
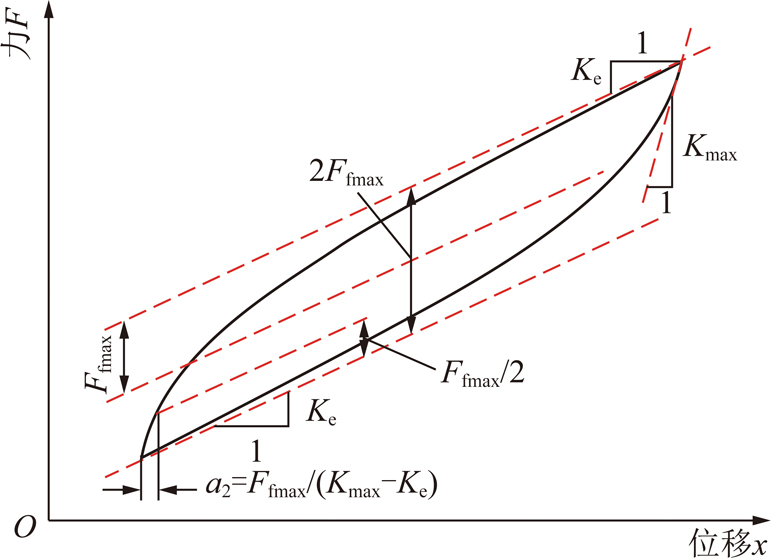
图5 迟滞环曲线中的模型参数
Fig.5 Model parameters in Hysteresis loop
表1 剪切弹簧非线性模型参数
Table 1 Parameters for nonlinear model of rubber shear spring

模型参数数值Ke/(N·mm-1)-0.003 1x30+0.192x20-4.504x0+207.77Ffmax/N0.007 7x30-0.519x20+16.322x0-10.547x2/mm-0.004 7x20+0.583x0-0.561α0.16b/(Nsα·mm-1)9.9
3 剪切弹簧非线性模型的实验验证
3.1 剪切弹簧力-位移迟滞环特性
当激振频率为0.01 Hz,激振振幅分别为3 mm和10 mm时,理论计算和实验测试得到的剪切弹簧迟滞环曲线,如图6所示;当激振振幅为4 mm,激振频率分别为1 Hz和6 Hz时,理论计算和实验测试得到的剪切弹簧迟滞环曲线,如图7所示。由图6,7可知,非线性模型理论计算与实验测试所得的迟滞环曲线在不同振幅及频率下均吻合良好,表明该非线性弹簧模型能够较好的描述剪切弹簧的动态特性。
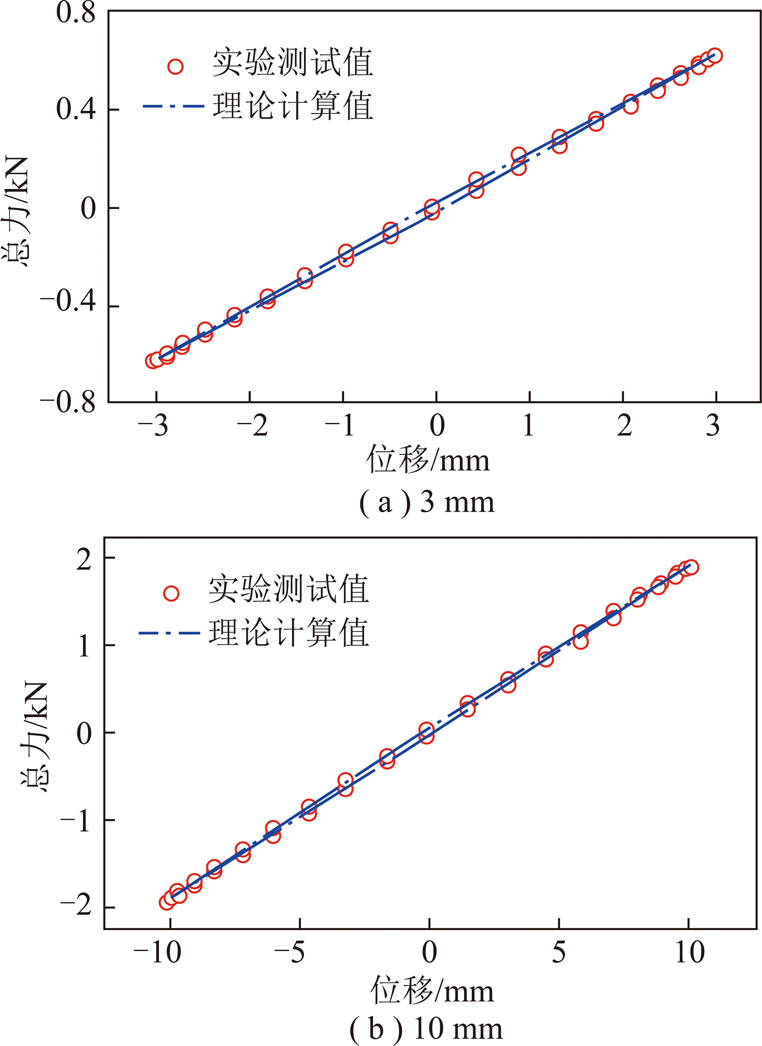
图6 不同振幅下迟滞环曲线测试值与计算值比较
Fig.6 Hysteresis loops compared between experiment and calculation for different amplitude
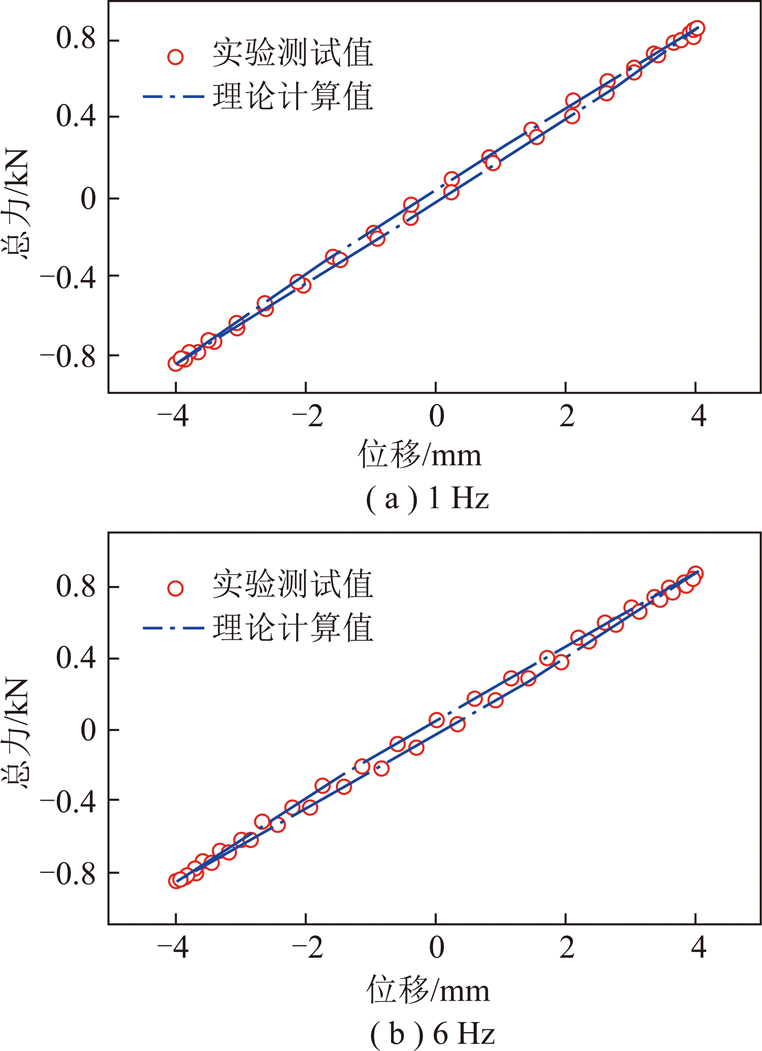
图7 不同频率下迟滞环曲线测试值与计算值比较
Fig.7 Hysteresis loops compared between experiment and calculation for different frequency
3.2 剪切弹簧动态特性的振幅和频率相关性
为了更直观的比较实验测试和新提出的模型理论计算所得剪切弹簧动态特性的振幅和频率相关性,需将实验测试以及理论计算所得到的迟滞环曲线根据式(1),(2)转化为动刚度和滞后角。首先取频率为0.01 Hz,消除黏滞力的影响[20,23-24],振幅区间为2~11 mm,来验证新提出模型中的非线性弹簧力和摩擦力在描述剪切弹簧动态特性振幅相关性时的合理性,结果如图8所示。由图8可得,剪切弹簧在该振幅区间,随着振幅的增加,弹簧动刚度及滞后角均减小。但常用的线性模型(Kevin-Voigt 模型)在描述弹簧动态特性的振幅相关性时,动刚度和滞后角不会随着振幅的变化而变化[24],显然不能用来准确描述剪切弹簧动态特性的振幅相关性。新提出的模型不仅可以描述剪头弹簧的振幅相关性,且弹簧动刚度及滞后角的理论计算值与实验测试值的平均方差分别仅为0.525和0.007,平均误差分别为0.323%和5.58%。与常用的线性模型相比,新提出的模型可更好的描述剪切弹簧动态特性的振幅相关性。
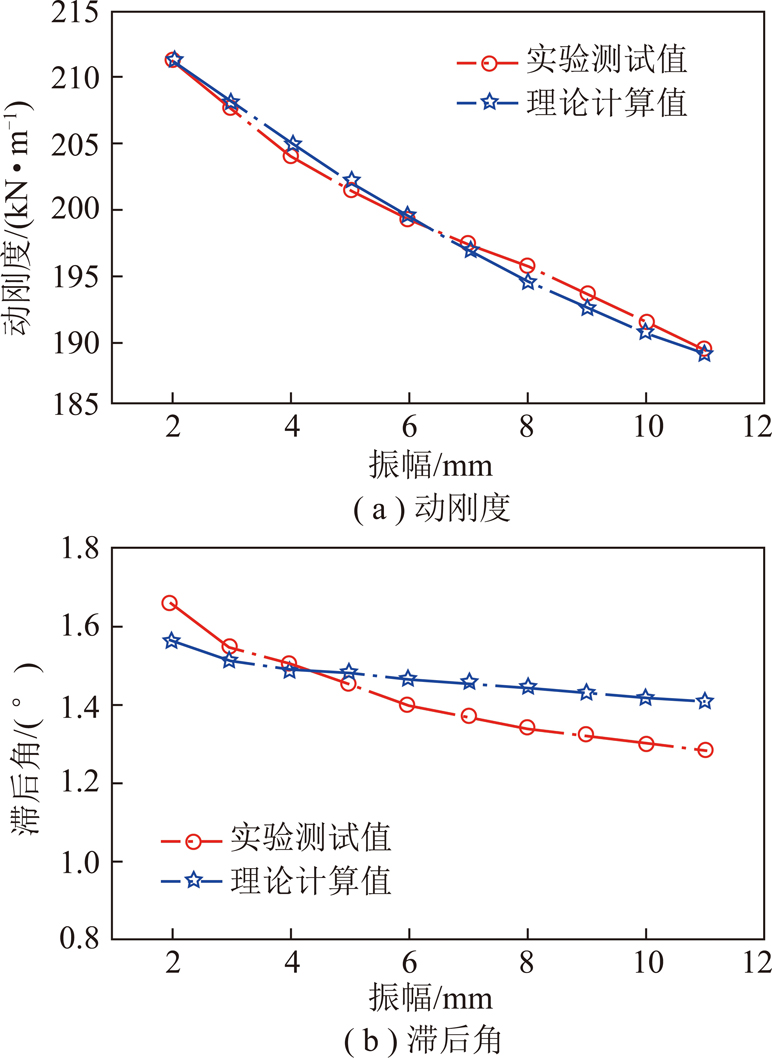
图8 不同振幅下动态特性测试值与计算值比较 Fig.8 Dynamic characteristics compared between experiment and calculation for different amplitudes
在验证新提出模型中的非线性弹簧力以及摩擦力在描述剪切弹簧动态特性振幅相关性时的合理性后,取振幅为4 mm,频率为1~6 Hz,同样将实验测试以及计算所得到的迟滞环曲线根据式(1),(2)转化为动刚度和滞后角,来验证新提出模型中的黏性力在描述剪切弹簧动态特性振幅相关性时的合理性[20,23-24],结果如图9所示。随着频率的增加,动刚度和滞后角在该频率区间内均呈现总体增加的趋势。但常用的线性模型在描述弹簧动态特性的频率相关性时,动刚度不会随着频率的变化而变化,滞后角会随着频率的变化而线性增加[17],显然不能用来描述剪切弹簧动态特性的频率相关性。新提出的模型不仅可以描述剪切弹簧动态特性的频率相关性,且弹簧动刚度及滞后角的理论计算值与实验测试值的平均方差分别仅为0.041和0.011,平均误差分别为0.107%和5.26%。表明新提出的模型相比常用的线性模型可较好的描述剪切弹簧动态特性的频率相关性。
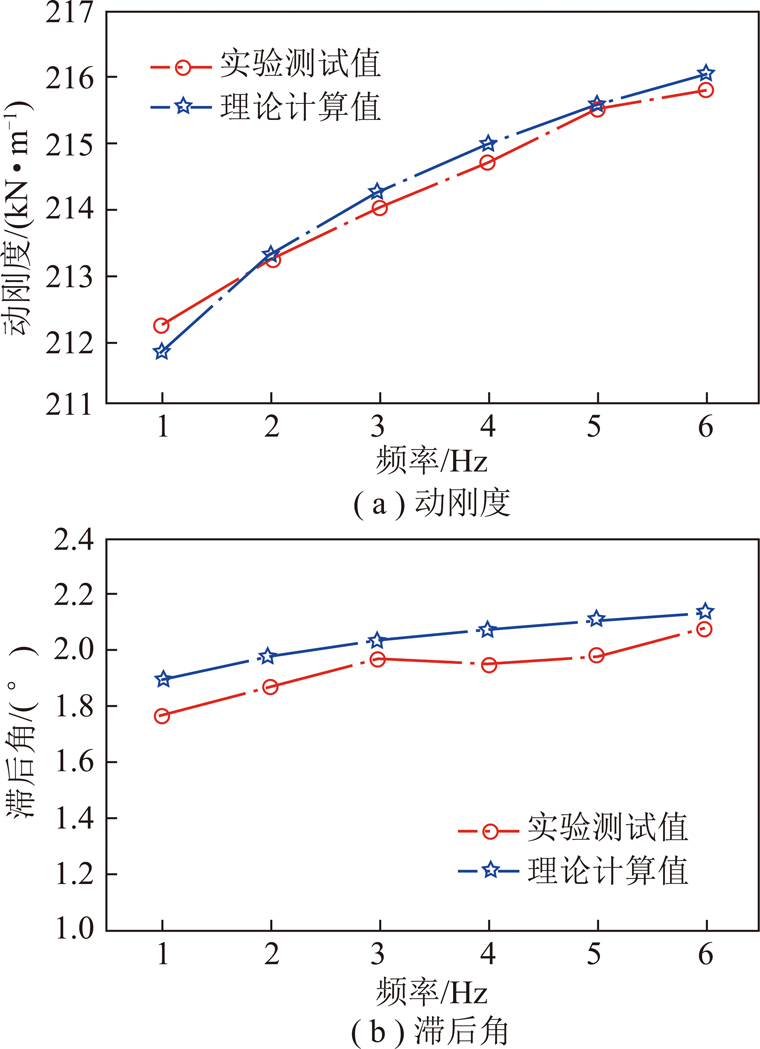
图9 不同频率下动态特性测试值与计算值比较
Fig.9 Dynamic characteristics compared between experiment and calculation for different frequencies
4 考虑剪切弹簧非线性模型的振动弛张筛力学模型
工业型振动弛张筛的结构示意图如图10所示,将剪切弹簧非线性模型应用于该弛张筛的动力学分析中,利用质量集中法建立该弛张筛的动力学模型,如图11所示。
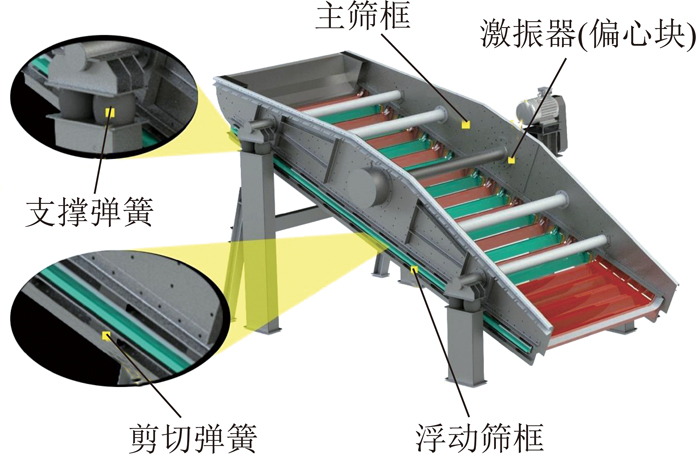
图10 振动弛张筛示意
Fig.10 Schematic of vibrating flip-flow screen
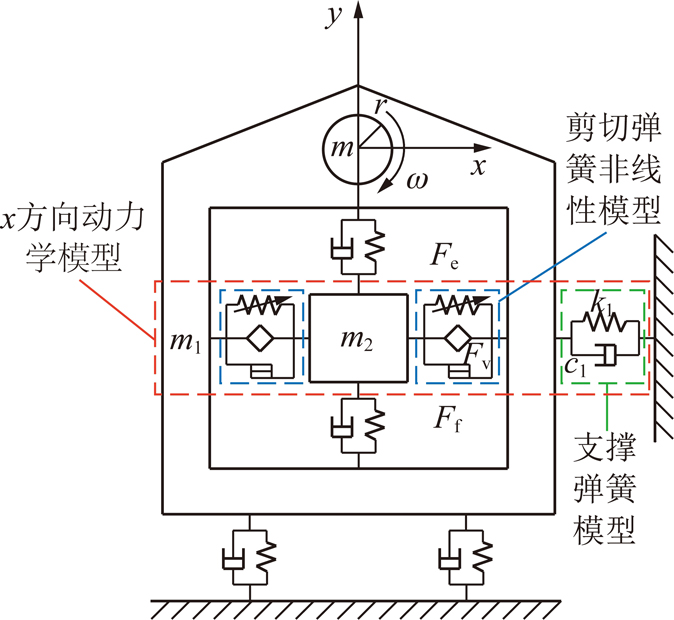
图11 振动弛张筛动力学模型
Fig.11 Dynamic model of vibrating flip-flow screen
图11中,m为激振器偏心块质量;m1和m2分别为主筛框和浮动筛框的质量;r为偏心块的偏心距;ω 为偏心块角速度;k1和c1分别为支撑弹簧的刚度和阻尼系数;x和y轴分别为平行和垂直筛板方向;该弛张筛受到的简谐激振力为F=F0cos ωt。由于影响筛面运动规律的因素主要是沿着筛面方向主浮筛框的振动,因此,本文只研究系统沿x方向的动力学响应,根据图11可得该振动弛张筛沿着x方向的动力学方程为
![]()
(11)
![]()
(12)
式中,x1为主筛框的位移; x2 为主筛框和浮动筛框的相对位移;F0为激振力的大小,F0cos wt为沿x方向激振力的大小;FE=24Fe,FF=24Ff和FV=24Fv是由于所研究的振动弛张筛中安装了24个剪切弹簧。
由于Fe为非线性函数,Ff为间断函数,Fv为分数导数函数,常规方法很难解方程组(11),(12)。本文将方程组(11),(12)转化为矩阵形式(13),并采用Newmark算法进行求解。
![]()
(13)
式中,M,C和K分别为振动弛张筛系统的质量、阻尼系数和刚度的矩阵形式;Fn,Xn分别为力和位移向量;![]() 和
和![]() 分别为系统的速度和加速度向量。
分别为系统的速度和加速度向量。
Newmark算法可以表示为
![]()
(14)
![]()
(15)
式中,β为控制方法特性的独立参数。
该算法稳定时的临界时间步长为![]() 为系统中最高无阻尼固有频率,取β=1/2可消除算法阻尼[17]。已知振动弛张筛系统的位移初值X(0)和速度初值
为系统中最高无阻尼固有频率,取β=1/2可消除算法阻尼[17]。已知振动弛张筛系统的位移初值X(0)和速度初值![]() 可采用以下流程图(图12)数值计算该系统的动力学响应。
可采用以下流程图(图12)数值计算该系统的动力学响应。
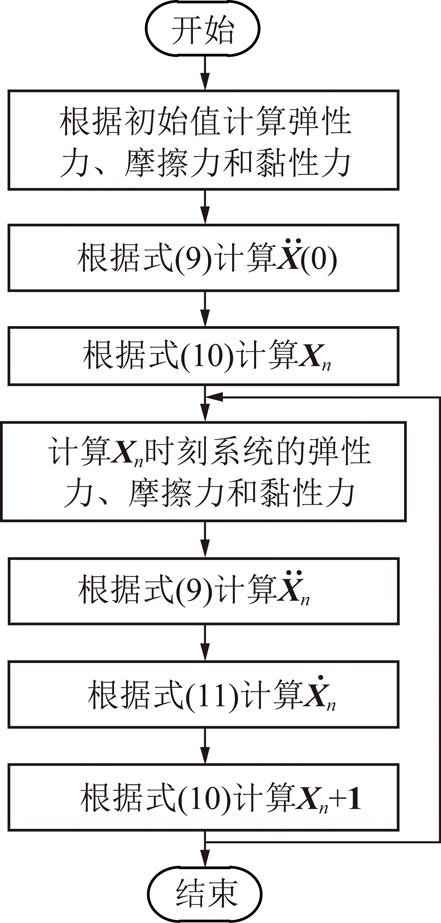
图12 计算流程
Fig.12 Flowchart for calculating
5 振动弛张筛系统参数对其动力学响应的影响
剪切弹簧和工业型振动弛张筛的相关参数分别见表1,2,振动弛张筛动力学系统的位移初值X(0)和速度初值![]() 都为0,按照流程图12,可计算该弛张筛在不同条件下的动力学响应。
都为0,按照流程图12,可计算该弛张筛在不同条件下的动力学响应。
表2 振动弛张筛参数
Table 2 Parameters for vibrating flip-flow screen

参数数值主筛框质量m1/kg4 130浮动筛框质量m2/kg1 309支撑弹簧刚度k1/(N·m-1)3 606 700支撑弹簧阻尼系数c1/(N·s·m-1)36 614激振器偏心块质量m/kg242.24偏心块偏心距r/mm25.48
5.1 剪切弹簧阻尼对系统动力学的影响
黏性模型中参数α的大小反应了剪切弹簧阻尼的大小,分别取α为0.2,0.3和0.4,得到不同阻尼下系统在二阶共振区内的动力学响应,如图13所示,由图可知,随着α的增加,x1和x2动力学响应的共振峰值减小,但共振频率增加,这是由于当阻尼增加时,系统振幅减小,剪切弹簧受到的激振振幅减小,其动刚度增加,故共振频率变大。但在振动弛张筛线性动力学响应分析中,随着剪切弹簧阻尼的增加,主浮筛框的共振幅值减小,共振频率不变[8,10],该研究表明在分析振动弛张筛动力学响应时,由于常用的线性弹簧模型不能准确描述剪切弹簧动态特性的振幅和频率相关性,其在分析振动弛张筛动态特性时会存在较大的误差,故研究振动弛张筛动力学响应时应考虑剪切弹簧的动态特性。
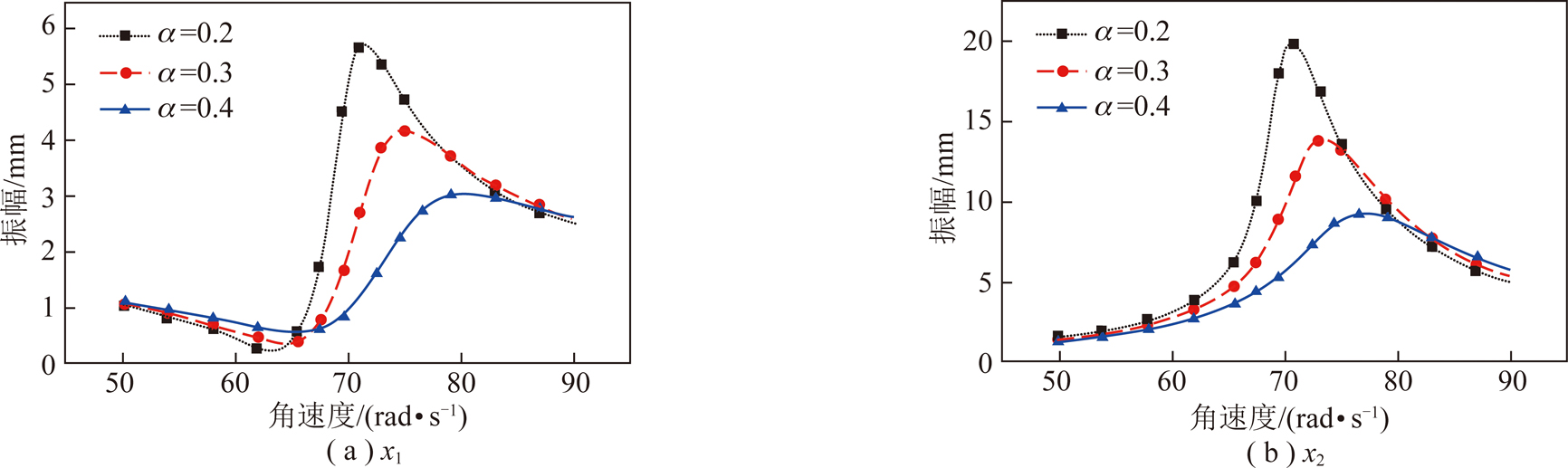
图13 不同阻尼下振动弛张筛动力学响应
Fig.13 Dynamic response of vibrating flip-flow screen for different dampings
5.2 激振力对系统动力学的影响
通过改变偏心块质量和偏心距来改变激振力的大小,得到不同激振力下系统在二阶共振区内的动力学响应,如图14所示。
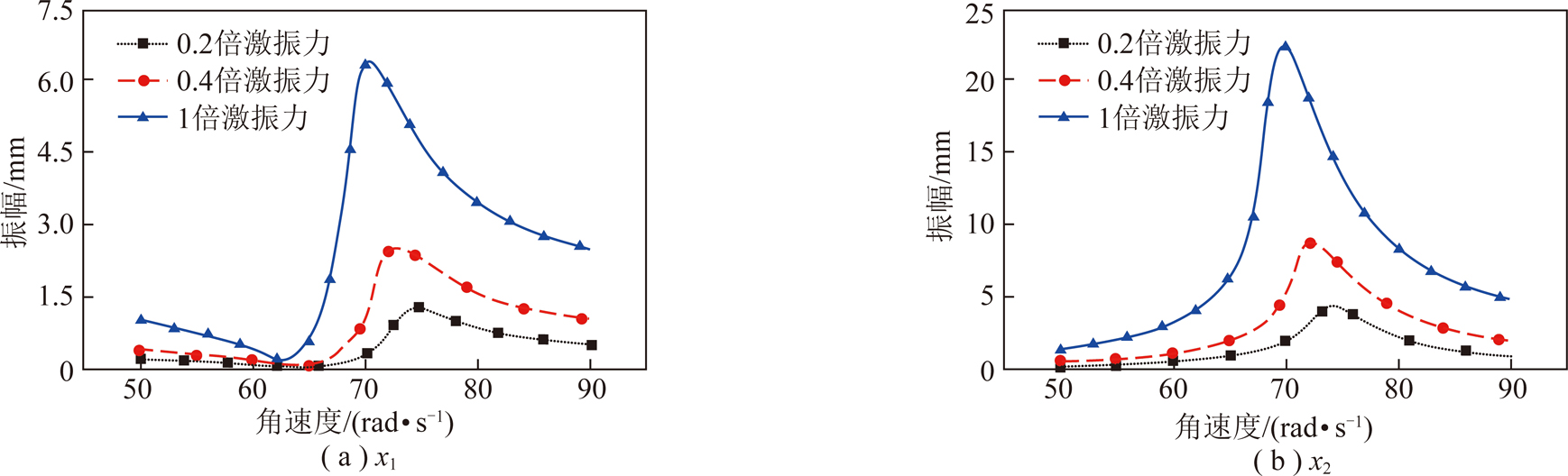
图14 不同激振力下振动弛张筛动力学响应
Fig.14 Dynamic response of vibrating flip-flow screen for different excitation forces
由图14可知,随着激振力的增加,x1和x2动力学响应的共振峰值增加,但共振频率减小,在振动弛张筛动力学的线性分析中,随着激振力的增加,x1和x2的共振峰值增加,但共振频率不变[8,10],该研究再次证明了用常用的线性振动弛张筛力学模型来预测其动力学响应时存在较大的误差,新提出的剪切弹簧非线性模型在预测振动弛张筛动力学响应时存在明显的优势。
6 结 论
(1)考虑剪切弹簧动态特性的振幅相关性和频率相关性,建立了剪切弹簧动态非线性模型,该模型由非线性弹性力、非线性摩擦力和采用分数阶导数形式的黏性力来表示,并通过实验测试验证了所建模型在表征剪切弹簧动态特性上的可行性,为其他橡胶弹簧的动态建模提供了理论参考。
(2)由于剪切弹簧动态特性具有振幅和频率相关性,随着剪切弹簧阻尼的增加,二阶共振区内,振动弛张筛的共振峰值减小,但共振频率增加,随着激振力的增加,振动弛张筛的共振峰值增加,但共振频率减小,故在研究振动弛张筛的动力学时,应考虑剪切弹簧的动态特性对系统的影响。
(3)相比常用的线性剪切弹簧模型,新提出的模型可以更好的预测剪切弹簧的动态特性以及振动弛张筛系统的动力学响应,为振动弛张筛的动态设计及优化提供了理论基础。
[1] MEINEL A.Fine and very fine screening[J].AT mineral processing English Edition,2010,51(1):1-8.
[2] GUPTA N.Evaluation of pneumatic inclined deck separator for high-ash Indian coals[J].International Journal of Coal Science & Technology,2016,3(2):198-205.
[3] DONG H L,LIU C S,ZHAO Y M,et al.Review of the development of dry coal preparation theory and equipment[J].Advanced Materials Research,2013,619:239-243.
[4] 宫三朋,王新文,赵国锋,等.振动弛张筛驱动位置对主浮筛框运动特性的影响[J].矿业科学学报,2018,3(5):1-7.
GONG Sanpeng,WANG Xinwen,ZHAO Guofeng,et al.Influence of the driving position of vibrating flip-flow screen on motion characteristic of main and floating screen frame[J].Journal of Mining Science,2018,3(5):1-7.
[5] PENG L,LI F,DONG H,et al.Characteristics analysis of a novel centralized-driving flip-flow screen[J].International Journal of Mining Science and Technology,2014,24(2):195-200.
[6] 刘初生,赵跃民.弛张筛筛面动态特性及其工艺参数的研究[J].中国矿业大学学报,2000,29(3):290-292.
LIU Chusheng,ZHAO Yaomin.Research on screen surface dynamic charaters and technical parameters of flip-flow screen[J].Journal of China University of Mining & Technology,2000,29(3):290-292.
[7] 彭利平,刘初升,董海林,等.弛张筛筛面大挠度非线性变形分析与实验[J].煤炭学报,2014,39(5):976-980.
PENG Liping,LIU Chusheng,DONG Hailin,et al.Analysis and experimental on the large nonlinear deformation of a flip-flow screen[J].Journal of China Coal Society,2014,39(5):976-980.
[8] XIONG X,NIU L,GU C,et al.Vibration characteristics of an inclined flip-flow screen panel in banana flip-flow screens[J].Journal of Sound and Vibration,2017,411:108-128.
[9] 陈志强,石剑锋,刘欣,等.双质体振动弛张筛振动特性分析[J].煤炭工程,2014,46(11):113-118.
CHEN Zhiqiang,SHI Jianfeng,LIU Xin,et al.Analysis on vibration characteristics of double mass vibrating flip-flow screen[J].Coal Engineering,2014,46(11):113-118.
[10] 宫三朋,王新文,于驰,等.有阻尼振动弛张筛主浮筛框运动规律的研究[J].煤炭工程,2018,50(8):126-132.
GONG Sanpeng,WANG Xinwen,YU Chi,et al.Study on the motion law of main floating screen frame of vibrating flip-flow screen with damping[J].Coal Engineering,2018,50(8):126-132.
[11] 翟宏新.基于幅频特性的工业型弛张筛合理工作点的确定[J].煤炭学报,2007,32(7):753-756.
ZHAI Hongxin.Determination of the operation range for flip-flow screen in industrial scale based on amplitude-frequency response[J].Journal of China Coal Society,2007,32(7):753-756.
[12] 邹梦麒,刘初升,武继达,等.张紧量对单边驱动式弛张筛筛面动力学参数的影响[J].煤炭学报,2018,43(2):571-577.
ZOU Mengqi,LIU Chusheng,WU Jiada,et al.Influence of tensional amount on dynamic parameters of unilateral driven flip-flow screen surface[J].Journal of China Coal Society,2018,43(2):571-567.
[13] LI Z,TONG X.A study of particles penetration in sieving process on a linear vibration screen[J].International Journal of Coal Science & Technology,2015,2(4):299-305.
[14] KNOTHE K L,GRASSIE S L.Modelling of railway track and vehicle/track interaction at high frequencies[J].Vehicle System Dynamics,1993,22(3-4):209-262.
[15] BABITSKY V I,VEPRIK A M.Universal bumpered vibration isolator for severe environment[J].Journal of Sound and Vibration,1998,218(2):269-292.
[16] FENANADER A.Frequency dependent stiffness and damping of railpads[J].Proceeding of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,1997,211(1):51-62.
[17] SÖJBERG M.Rubber isolators-measurements and modeling using fractional derivatives and friction[J].SAE technical paper series,2000,2000-01-3518.
[18] SÖJBERG M.Non-linear behavior of a rubber isolator system using fractional derivatives[J].Vehicle System Dynamics,2002,37(3):217-236.
[19] KAI S,SVEN D,JOCHEN R.Advanced modular modelling of rubber bushing for vehicle simulations[J].Vehicle System Dynamics,2011,49(5):741-759.
[20] ZHU S,CAI C,POL D Spanos.A nonlinear and fractional derivative viscoelastic model for rail pads in the dynamic analysis of coupled vehicle-slab[J].Journal of Sound and Vibration,2015,335(20):304-320.
[21] BERG M.A model for rubber springs in the dynamic analysis of rail vehicles[J].Proceeding of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,1997,211(2):95-108.
[22] BERG M.A non-linear rubber spring model for rail vehicle dynamics analysis[J].Vehicle System Dynamics,1998,30(3-4):197-212.
[23] ZHU H,YANG J,ZHANG Y,et al.A novel air spring dynamic model with pneumatic thermodynamics effective friction and viscoelastic damping[J].Journal of Sound and Vibration,2017,408:87-104.
[24] SHI H,WU P.A nonlinear rubber spring model containing fractional derivatives for use in railroad vehicle dynamic analysis[A].Proceeding of the Institution of Mechanical Engineers(Part F)[C]:Journal of Rail and Rapid Transit,2016,230(7):1745-1759.
