对于煤层顶板的定义,从岩层沉积年代角度来说,一般将位于煤层之上,在煤层形成之后形成的岩层称为顶板[1];从煤矿开采工程实践角度来说,一般将位于煤层上方的岩层称为顶板[2]。近直立特厚煤层顶板与传统的缓、倾斜煤层顶板有着本质的区别。近直立特厚煤层的顶板是由“顶板侧”岩层、“上覆煤层”、“底板侧”岩层3种煤岩体组合而成,其顶板不再是传统意义上的单一岩层顶板,而是煤岩体组合形成的复杂顶板。众多学者就急倾斜特厚煤层开采进行了大量的相关研究[3-10]。张勇等从裂移度[3]、放出率[4-5]、裂隙扩展[6]等方面对急倾斜煤层开采进行了深入细致的研究,并取得了一系列的成果;张宏伟等[7-8]基于地质动力区划法,对乌东煤矿近直立特厚煤层冲击地压危险性进行了评价;王宁波等[9]通过对急倾斜特厚煤层综放工作面覆岩结构与应力分析和巷道分区破坏的力源条件进行分析,认为对急倾斜特厚煤层围岩破碎具有分区特征;屠洪盛等[10]对急倾斜工作面顶板初次变形破断特征研究,得出倾斜工作面下部采空区充填带宽度的理论计算公式和顶板变形挠度方程。除此之外,众多学者对直接顶的力学结构、应力分布、破断规律进行了大量的研究[11-14],杜峰等[11]对薄基岩综放开采直接顶的力学结构进行了分析,建立了薄基岩综放开采直接顶结构力学模型;高峰等[12]根据砌体梁理论对直接顶受力变形进行了分析;张自政等[13]建立了沿空留巷充填区域直接顶弹性损伤力学模型,对充填区域直接顶应力分布特征进行了研究;蔡峰等[14]对直接顶沿空留巷切顶断裂条件及围岩移动规律研究,推导出巷道顶板支护阻力的计算方法。近直立特厚煤层在开采的过程中,不仅会面临“顶板侧”岩层、“上覆煤层”移动和垮落的问题,而且还会面临比倾斜及缓斜煤层更加复杂的“底板侧”岩层顶板出现滑移或倾覆破坏的问题。随着煤层倾角的增大,直接顶的破坏对采场和巷道的影响逐渐凸显,基本顶的破坏对采场和巷道的影响逐渐减弱。
近直立煤层直接顶的破坏会导致大面积的煤岩体突然冲到工作面及两巷,造成巷道急剧变形,设备掀翻,人员掀倒,甚至引发严重的冲击地压灾害事故,给煤矿安全、高效的生产带来严重威胁,因此,研究近直立煤层开采过程中直接顶初次破断时的破断位置、以及破断演化过程对近直立煤层开采有着借鉴意义。
1 工程背景
阿刀亥矿区内地形十分复杂,悬崖陡峭,山高谷深,“V”字型冲沟发育。地表基岩裸露,植被十分稀少,覆盖率很低。矿区开采煤层近于直立,采空区形成的地面塌陷面积小,仅为一狭长的条带,但随着开采深度的逐渐延深,地面塌陷范围扩大。阿刀亥矿煤层倾角平均76°,最高为86°,近于直立,煤层厚度平均为26 m,采用水平分段综放开采方法,分段高度为16 m,采煤高度为2.2 m,放煤高度为13.8 m(已备案),如图1所示。
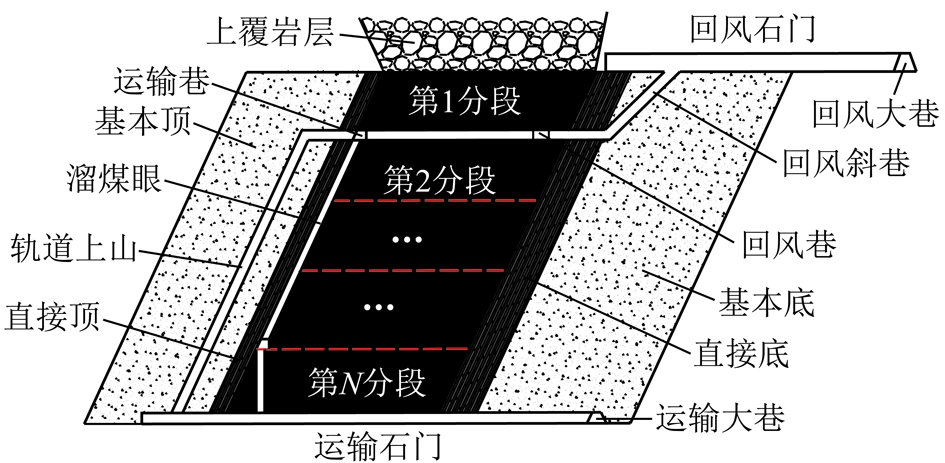
图1 水平分段放顶煤巷道布置示意
Fig.1 Diagrammatic sketch of SLTCC
阿刀亥矿开采煤层强度低,顶板厚度大且致密坚硬,较难垮落,这与其它急倾斜煤层矿区的开采条件差别很大,其顶底板情况见表1。
表1 煤层顶底板条件
Table 1 Conditions of seam roof and floor
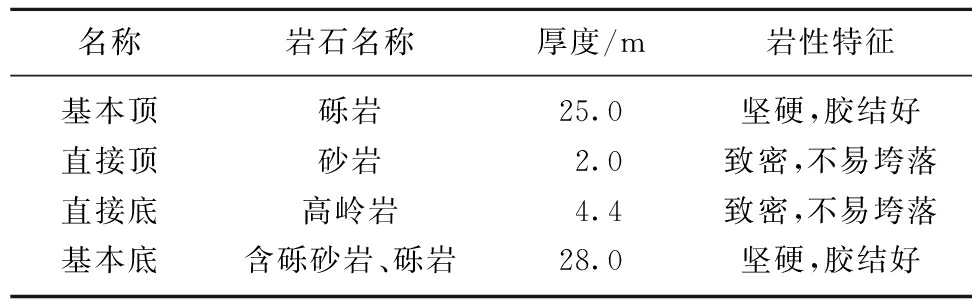
由于直接顶厚度水平分段高度的斜长之比在0.121~0.125,满足弹性薄板的基本假设[15],因此将采用弹性薄板理论对急倾斜分段放顶煤的直接顶初次破断特征进行分析。
2 近直立特厚煤层直接顶力学模型
2.1 近直立特厚煤层开采过程来压特征
近直立特厚煤层采用水平分段放顶煤开采时,工作面上方是“岩层-煤层-岩层”组成的复合顶板,由于煤层的强度低于两边的岩层强度,顶板煤层先于顶板岩层破坏、垮落、放出,采空区上方形成较大的空间,而采空区充填率低,造成工作面上方岩层活动更加剧烈。由于煤层倾角较大,在煤层开采后,岩层法向上的作用力(即岩层间的相互作用力)变化较大,紧邻开采空间的直接顶法向应力变化尤为明显;而在岩层倾斜方向和走向方向上的应力变化较小,顶煤上方岩层能够形成相对稳定的“铰接岩板”和“压力拱”结构,随着开采空间的进一步加大,采空区空间逐渐加大,上部岩层形成的“铰接岩板”和“压力拱”结构逐渐由稳态到非稳态,进而发生破坏,其破坏形式主要有弯曲折断、旋转破坏、整体失稳滑落、水平移动等,直接顶岩层法向应力状态的变化直接影响直接顶岩层的破坏特征。
近直立煤层工作面回采过程中岩层的破坏是多种破坏形式的组合,距离开采空间近的岩层(直接顶和直接底)破坏形式较为复杂,远离开采空间的岩层(基本顶和基本底)破坏形式相对简单,原因在于距离开采空间越远的岩层周围应力场变化较小。因此,直接顶的破坏将直接影响采场和巷道的矿压显现。与此同时,近直立特厚煤层工作面来压相比其他赋存条件下的煤层具有来压更复杂、更剧烈的特点。
2.2 伽辽金法
弹性薄板的弯曲问题只有在极少数情况下可以直接求出精确解,通常情况下,一般通过间接方式进行求解,是除了三角级数解法外,经常采用的另一种基于极值原理的能量法。
三维线弹性体的应变能密度为
σ23γ23+σ31γ31)
(1)
式中,W为线弹性体应变能密度;σ11,σ22,σ33,σ12,σ22,σ31为应力;ε11,ε22,ε33为体积应变;γ12,γ23,γ31为扭转应变。
对于薄板小挠度弯曲问题,根据薄板理论的基本假设不考虑ε33,ε32,ε31,因此其应变能可以表示为
∭v(σ11ε11+σ22ε22)dx1dx2dx3
(2)
式中,U为线弹性体应变能。
由弹性力学以及胡克定律可得薄板的应力、应变与板的挠度关系,即
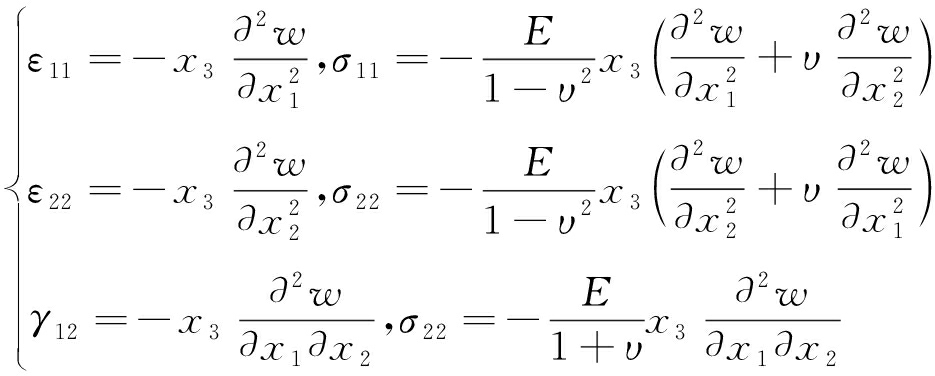
(3)
式中,w为弹性薄板挠度;υ为泊松比;E为弹性模量。
将式(3)代入式(2)中,整理后用挠度w表示应变能为
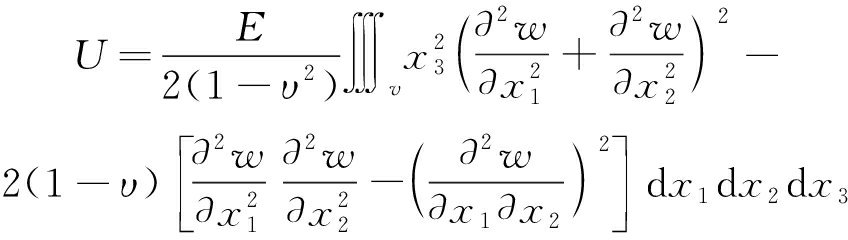
(4)
将式(4)沿板厚度h方向进行积分,整理得
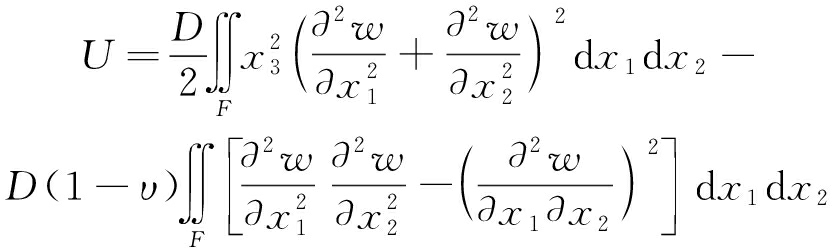
(5)
式中,F为弹性薄板的长和宽范围;D为弹性薄板的弯曲刚度,D=Eh3/12(1-υ2);h为薄板厚度。
对于边界固定的矩形板,即在四周边界处w =0时,则式(5)的右边第2项积分为0,因此四周边界挠度w =0的矩形板的应变能为
(6)
若板只受法向载荷P(x,y)作用,则外力势能为
(7)
式中,V为外力作用下的势能;P(x,y)为弹性板所受载荷分布函数。
将式(6)和(7)相加即可得到整个板的弹性位能
П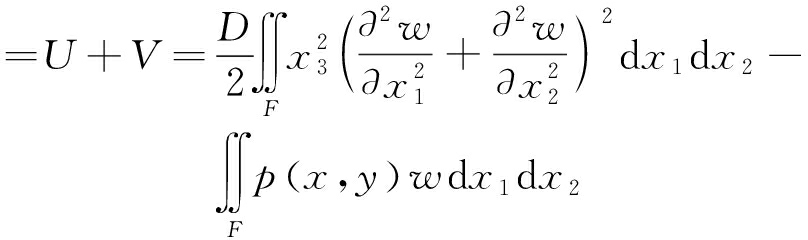
(8)
式中,Π为弹性薄板弹性位能。
当式(8)的位能Π取极值的w就是薄板弯曲问题的解。一般来说这样的精确解不易求出,因此,笔者采用伽辽金法分别对上文中所建的四边固支板模型求解近似解。
用伽辽金法求解薄板弯曲问题时,所设的挠度w方程为
(9)
其中,φij为满足板的全部边界条件的函数方程;Amn为待定常数。式(9)不一定能使平衡方程各个位置都精确对应,而会出现残量,X =DΔ4φij-P(x,y),伽辽金要求残量X在薄板中性面域内以试验函数φij为权的权积分为0,即
(10)
式中,Δ2为拉普拉斯算子,![]()
2.3 近直立特厚煤层直接顶挠度方程求解
开采近直立特厚煤层时,在直接顶初次破断之前,直接顶在“铰接岩板”和“压力拱”结构的作用下可以形成较稳定的结构,其端部被未破坏煤体和深部岩体固定,因此将近直立煤层直接顶在初次破断前直接顶岩层简化成四边固支板,如图2所示。
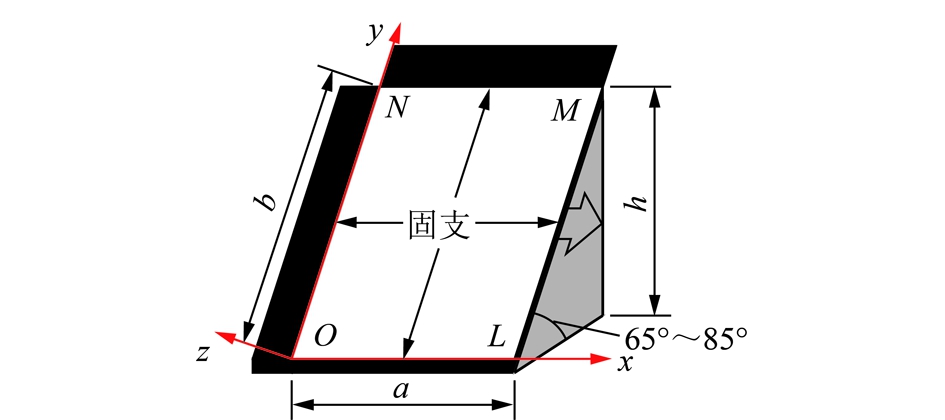
图2 四周固支力学模型
Fig.2 Four edges clamped plate model
图2中的OL,LM,ON,MN四边受实体煤支撑可以简化为固支,其力学模型的边界条件为
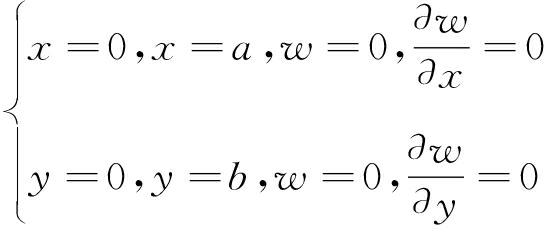
(11)
式中,a为弹性薄板的走向长度;b为弹性薄板的倾斜长度。
根据四周固支板边界条件,依据伽辽金法假设挠度表达式为
(12)
显然它满足所有边界条件(11),将挠度表达式(12)代入式(10)整理,求解出四周固支板在载荷设为P(x,y)作用下的通解为
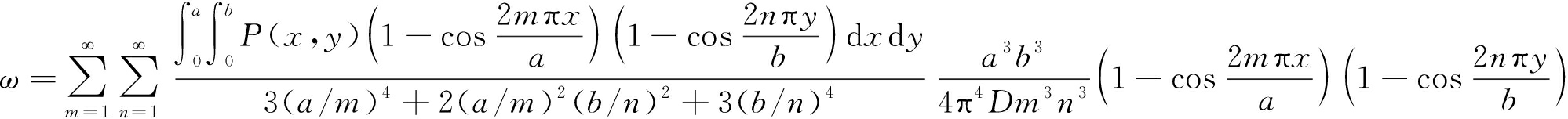
(13)
3 直接顶法向应力分布特征
3.1 直接顶法向应力数值模型建立
在求解四周固支板模型的挠度方程的过程中,薄板所受法向应力用未知参量P(x,y)代替,然而工程实践中很难监测水平分段放顶煤直接顶法向应力分布特征,因此将采用FLAC3D数值模拟方法来模拟水平分段放顶煤开采过程中的直接顶法向应力分布规律。同时考虑到煤层埋深、倾角、地应力分布等因素将会对直接顶应力分布造成影响,因此采用正交设计[16-18]的方法研究在4种因素3个水平下的直接顶法向应力分布,具体的正交试验设计方案见表3。
表3 基于L9(34)正交试验设计方案
Table 3 Simulations of nine representative combinations,based on the orthogonal array L9(34)
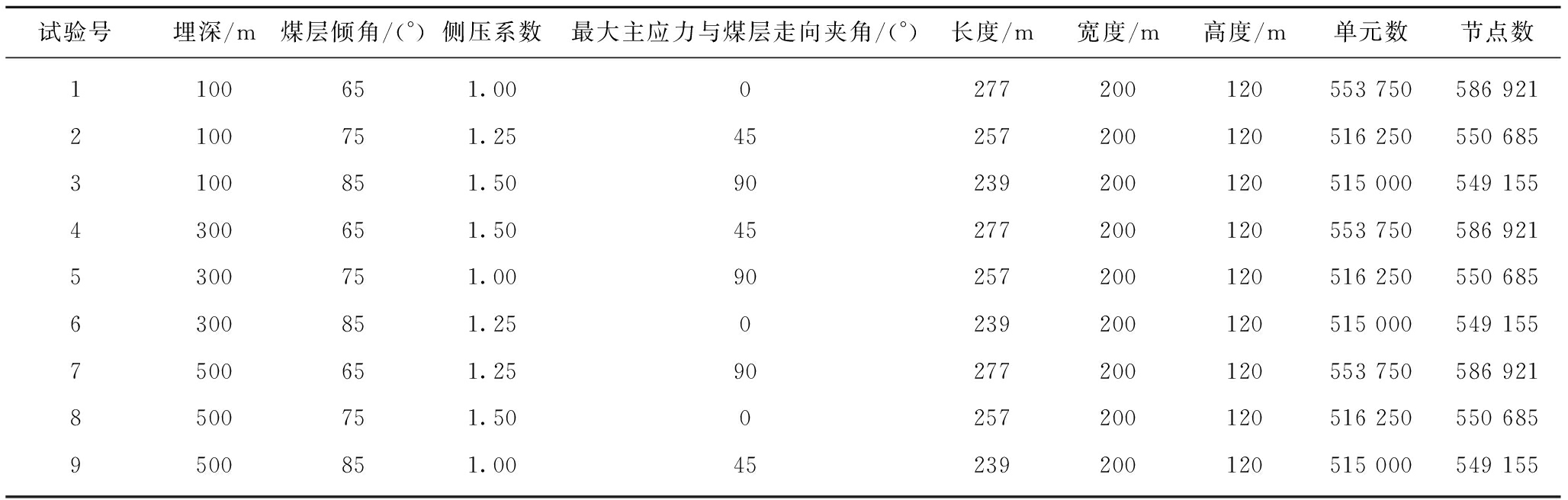
模拟过程关于埋深和地应力的变化通过采用改变数值模型的边界条件来实现,通过在模型上部施加垂直应力来模拟不同埋深的条件下顶板在煤层开采过程中的应力环境,通过改变x和y方向的应力和位移边界条件来模拟不同水平主应力和不同侧压系数条件下的顶板的应力环境。
跟据经验垂直应力σ与埋深H正相关[19],即σ=γH,其中容重γ根据经验取25 kN/m3,根据材料力学最大主应力及其方位角计算公式[20]
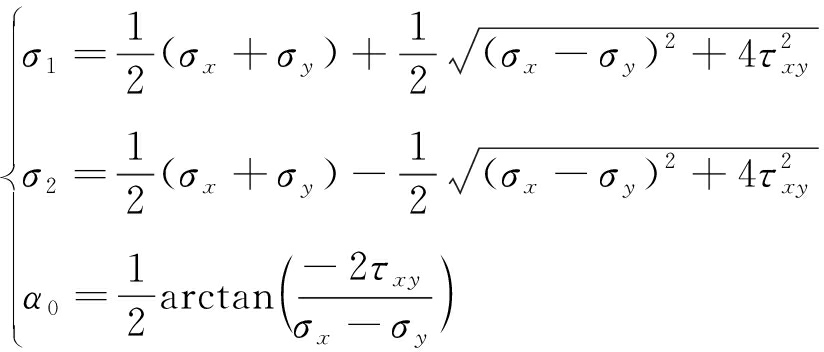
(14)
式中,σ1,σ2分别为平面内最大水平主应力、最小水平主应力;σx,σy分别为x,y方向的应力;τxy为平面内的剪应力;a0为最大水平主应力方向角。
由于在模拟过程中需要对边界施加边界条件,多数情况主应力以及方向角是已知的,需要由主应力σ1,σ2和方向角α0来反算作用在模型边界上的σx,σy,因此需要在式(14)的基础上进行转化,即
(15)
由于多数情况下最大水平主应力σ1与最小水平主应力σ2的差值较大,通过统计17个矿井地应力测试结果见表4,经计算,σ1/σ2的平均值为1.80,因此数值模拟中的σ1/σ2的取1.80。
表4 部分煤矿地应力现场测试统计
Table 4 In-situ stress of field measurement case
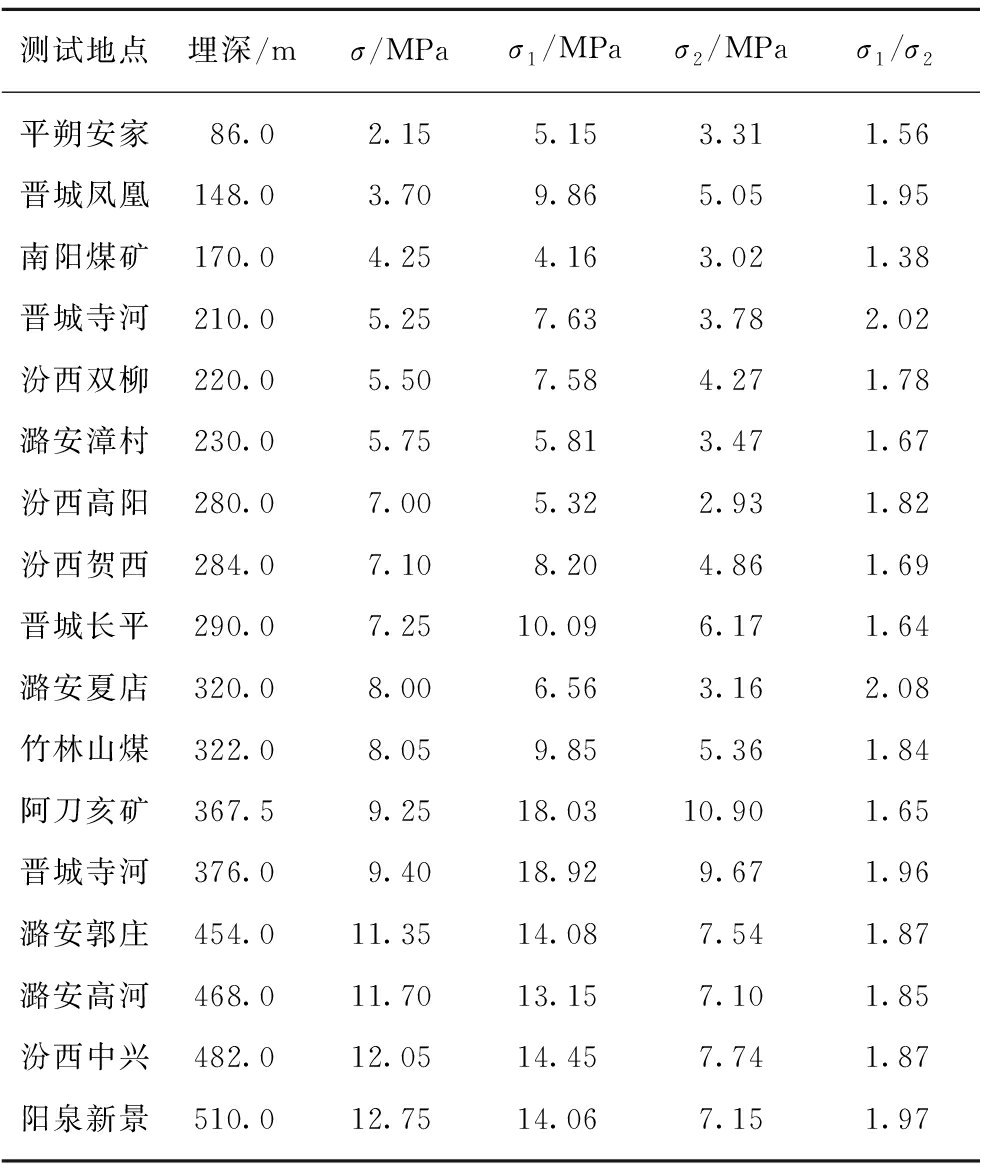
正交试验方案中煤层倾角的模拟主要是通过建立3类不同岩层倾角的数值模型来实现,如图3所示。
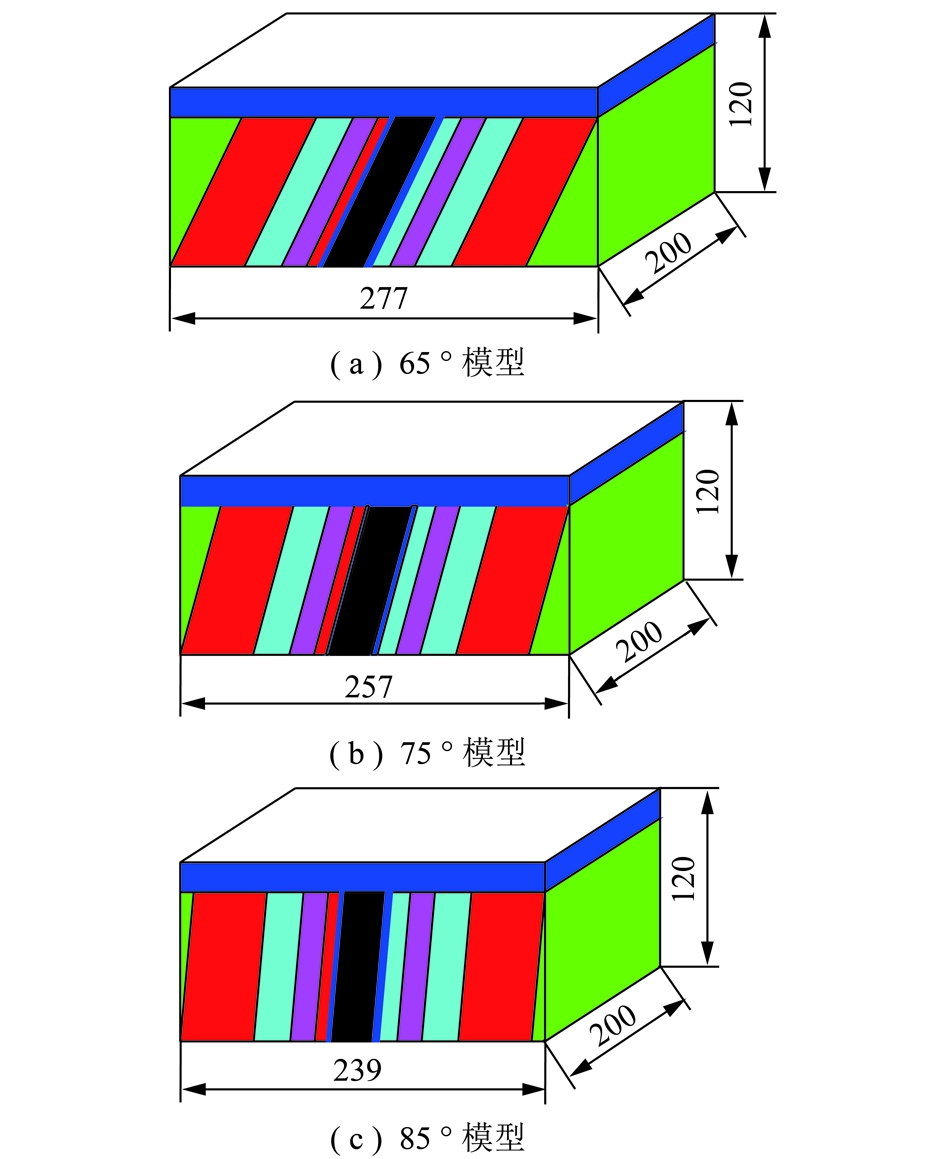
图3 3种不同倾角模拟模型
Fig.3 Simulation model of three different inclination
9组数值模拟模型的边界采用3面限定位移和3面施加应力的形式,如图4所示,对应的9组数值模型边界施加的应力情况,见表5。
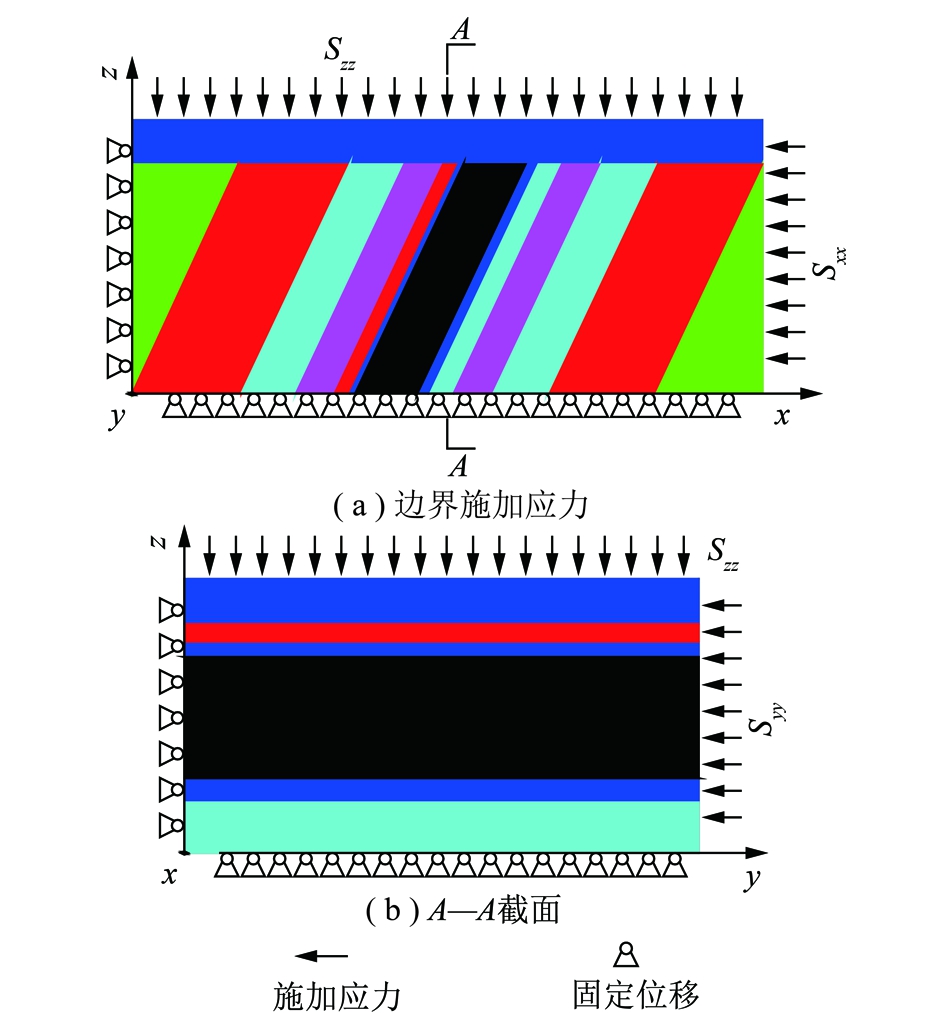
图4 边界条件示意
Fig.4 Schematic diagram of boundary condition
岩层顶板的直接顶通常是由多种岩层构成,具有相近的力学性质,在数值分析中通常简化成一种岩层,根据阿刀亥矿井的实际岩层情况,将模型简化成13种煤岩层,见表6。
表5 数值模型边界条件
Table 5 Boundary condition of numerical model
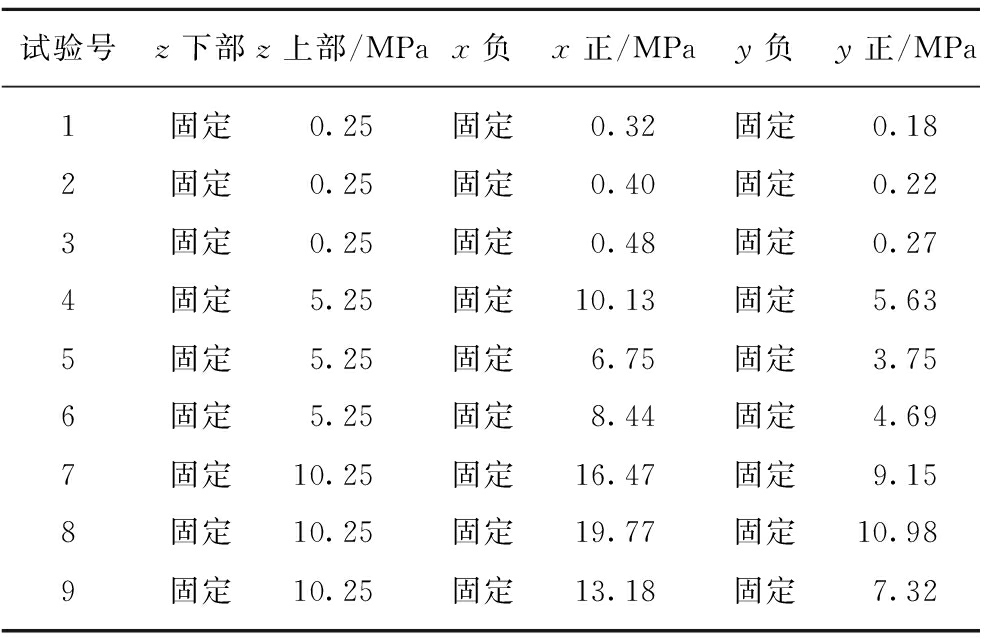
岩层的破坏准则采用摩尔-库伦强度准则。初始平衡后,分别对上下两分段进行开挖,每个分段均开挖80 m,工作面推进方向两端分别留60 m的边界影响区,工作面开挖采用分步依次开挖,每次开挖4 m,由于文章篇幅所限不能对所有的开挖过程进行分析,因此只对模拟过程中的部分实验结果进行分析,即上分段开挖20,40,80 m以及上分段开挖完成后下分段开挖20,40,80 m的模拟结果。
3.2 应力转换
由于FLAC3D数值模拟出的直接顶岩层的应力数据不能直接作为薄板力学模型的边界条件进行直接求解,因此需要对应力数据进行转换,即在不同坐标系下应力的转换,将FLAC3D中处于空间直角坐标系下的应力转换为以岩层走向、倾斜方向和法向方向为坐标轴方向的新坐标系下的应力数据,数据在两个坐标系转换的过程中岩层走向方向未发生改变,因此坐标转换的过程可以看成沿岩层走向(y轴)进行旋转,如图5所示。
表6 主要煤岩层力学参数
Table 6 Primary mechanical parameters of coal or rock stratum
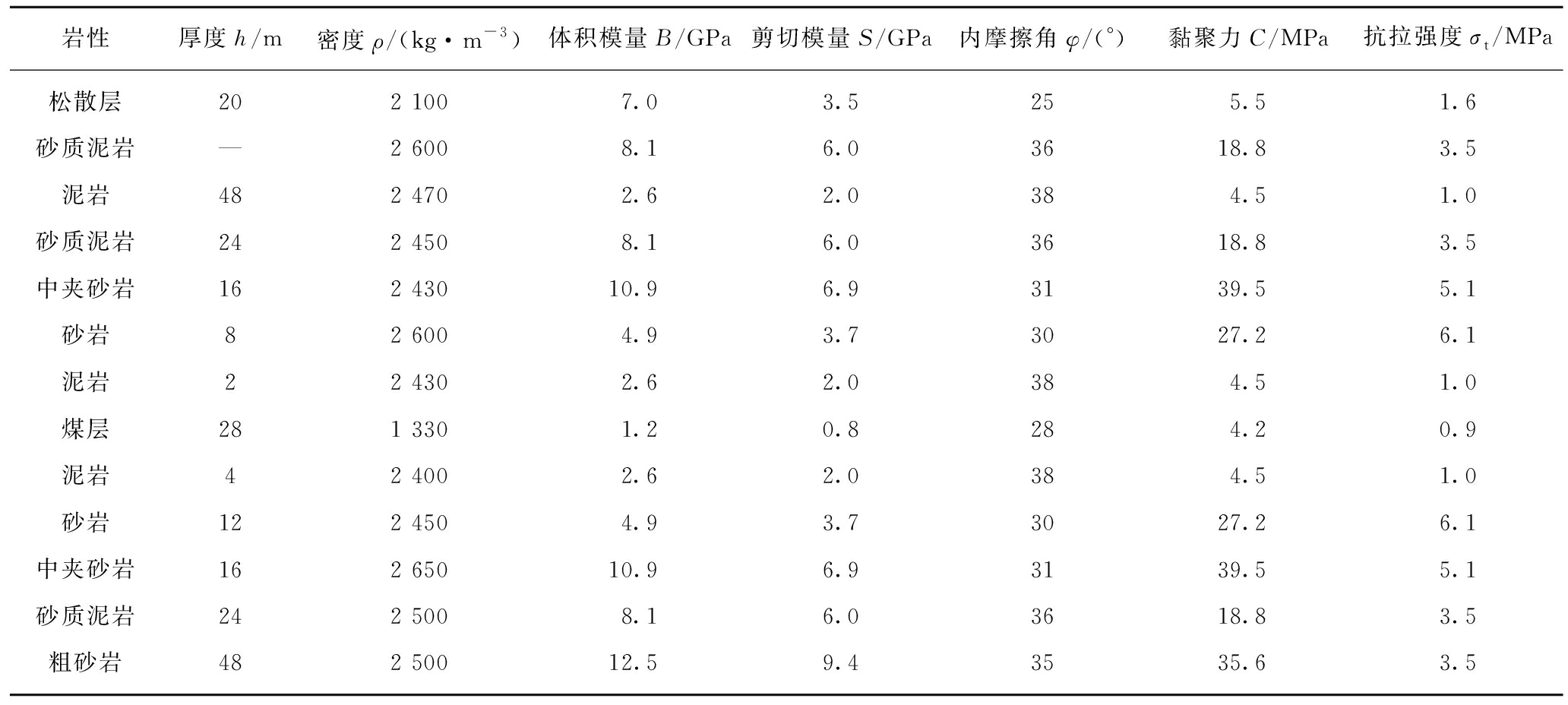
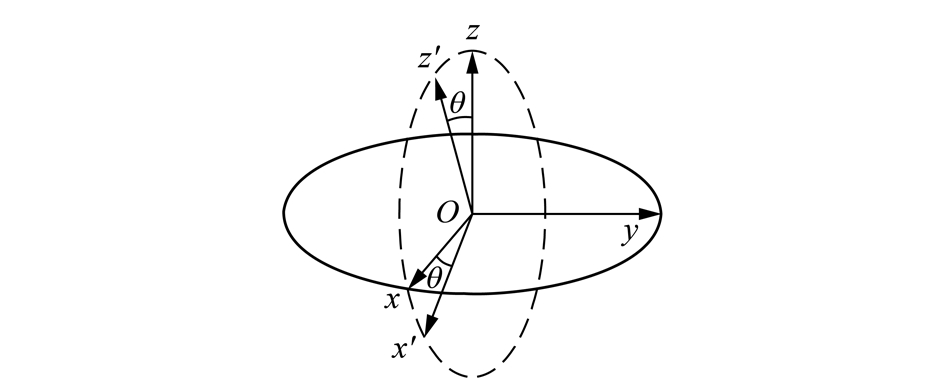
图5 坐标系旋转示意
Fig.5 Diagram of SCCS rotation
正应力在两个坐标系下的转化关系为
(16)
式中,σx′,σz′分别是新坐标系下的应力。
3.3 直接顶法向应力分布特征分析
依据式(16)将数值模拟中的应力转换成直接顶法向应力,在工作面推进长度的中间部位选取测线,对比分析9种正交试验的法向应力分布特征,法向应力沿倾斜方向的分布特征如图6所示。
通过对前面9组试验的初步分析可以将采空区上方岩层顶板法向应力分成两部分,一部分是边缘应力增高区,其范围是距离边缘4 m左右的范围;另一部分是近似均值的平滑部分,该部分的应力可以看成是均匀分布。为了更加充分的分析埋深、倾角、侧压系数以及最大主应力与岩层走向方向4种因素对近直立特厚煤层分段开采顶板法向应力影响的大小关系,为此对上述4种因素又进行了方差分析,计算出了每种参数对实验结果的影响权重,结果表明:在距离边缘4 m左右的范围内,对其顶板法向应力分布均值影响作用由高到低分别为倾角>埋深>最大水平主应力与岩层走向夹角>侧压系数;在近似为均匀分布的平滑区域内,对其顶板法向应力分布均值影响作用由高到低分别为最大水平主应力与岩层走向夹角>倾角>埋深>侧压系数。虽然不同参数对法向应力分布特点有一定的影响,但法向应力的分布趋势基本一致,除去直接边缘处的边缘效应的影响,可以将直接顶的法向应力近似看成是均布载荷。
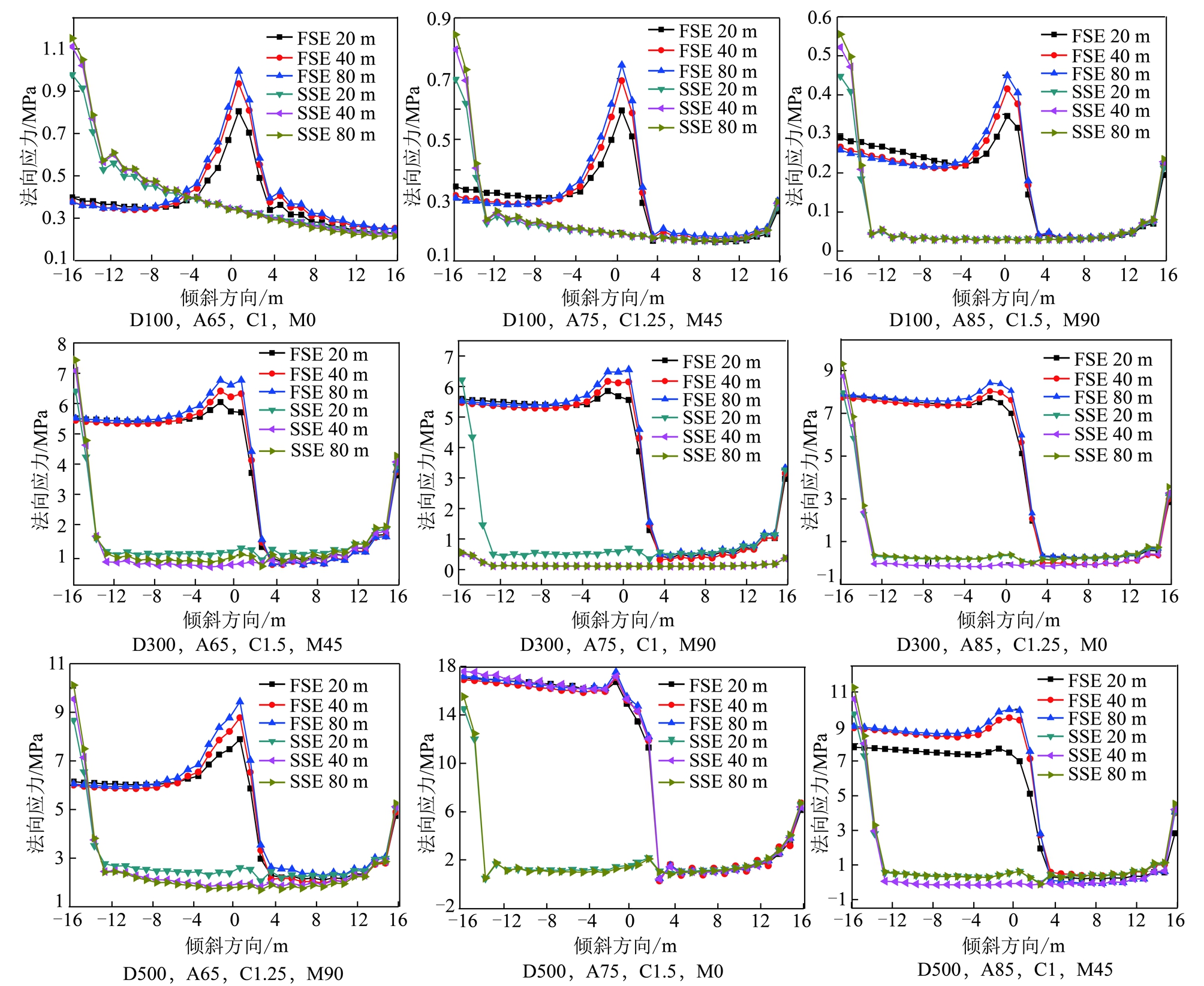
图6 沿倾斜方向法向应力分布特征曲线
Fig.6 Normal stress distribution of immediate roof in the direction of dip
FSE为第1分段开挖长度,SSE为第2分段开挖长度,D为埋深,A为煤层倾角,C为侧压系数,M为最大水平应力与煤层走向的夹角
4 直接顶岩层初次破断分析
4.1 直接顶岩层破坏判别依据
脆性材料的破坏通常是瞬间快速断裂[21],断裂前变形较小,塑性指标较低,材料的抗拉强度远远小于其抗压强度。在分析岩石材料的破坏过程中,通常将岩石材料看成脆性材料,其破坏与应力场有关[22],可以采用岩石材料的抗拉强度作为判定采场上方顶板破坏的依据,因此采用最大拉应力强度理论作为顶板岩层的破坏依据,即
βσu=σc
(17)
式中,β为岩石和岩体抗拉强度折减系数;σu为顶板岩石的最大抗拉强度,MPa;σc为顶板中的最大拉应力,MPa。
当弹性薄板在法向方向产生挠度时,薄板产生弯曲,其中线面可以简化成一个空间曲面,同时由于薄板的边缘固定,薄板各个方向的弧长大于两个固定端的长度,随着长度的增加,薄板的应力状态将以拉应力为主。
假设破坏前的岩层顶板是连续的弹性薄板,在此阶段仅考虑其工程结构中发生的小变形。依据偏微分方程原理,可以将薄板的中性面分解成无数无限小的薄板微元,假设每个微元分别在x和y方向都可以简化成无限短的直线,设其变形前的长度分别为dx,dy,变形后其对应的长度变为dsx,dsy,如图7所示。
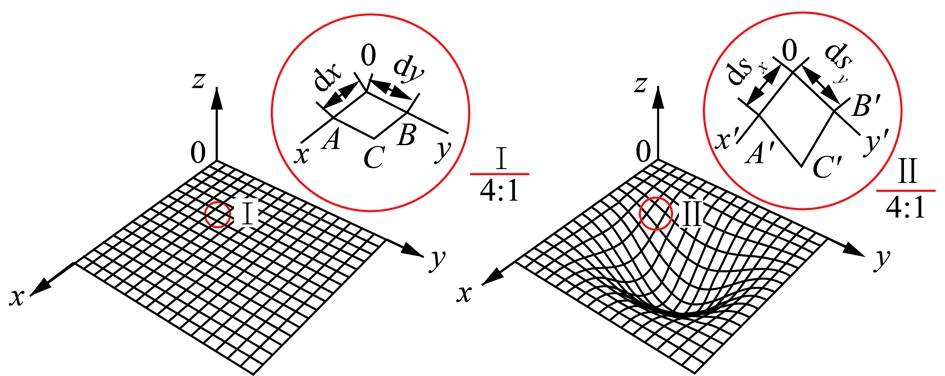
图7 弹性板变形前后示意
Fig.7 Deformation of the elastic thin plate
根据弧长公式可知dx,dy,dsx,dsy和挠度w关系为
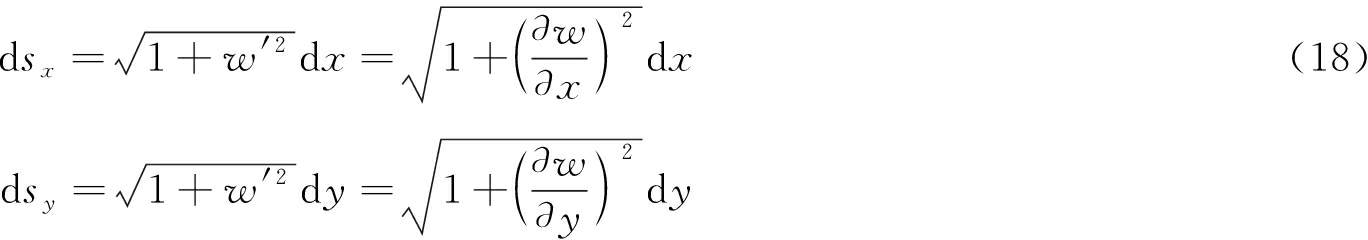
(19)
考虑到岩体的非均质性以及各向异性,可以认为岩体各个位置产生的变形不同,因此产生的应变不同,由于将薄板中性面分割成无限小的微元,每个微元可以看成连续、均质、各向同性的介质,根据线应变定义,可以认为薄板在x方向和y方向各微元的应变为

(21)
根据广义胡克定律和弹性薄板相关理论,由于不考虑与板垂直面上的应变,即认为εz=0,τxz=0,τyz=0,因此 对式(20)和(21)进行整理可以获得弹性薄板拉应力与薄板挠度的关系方程:
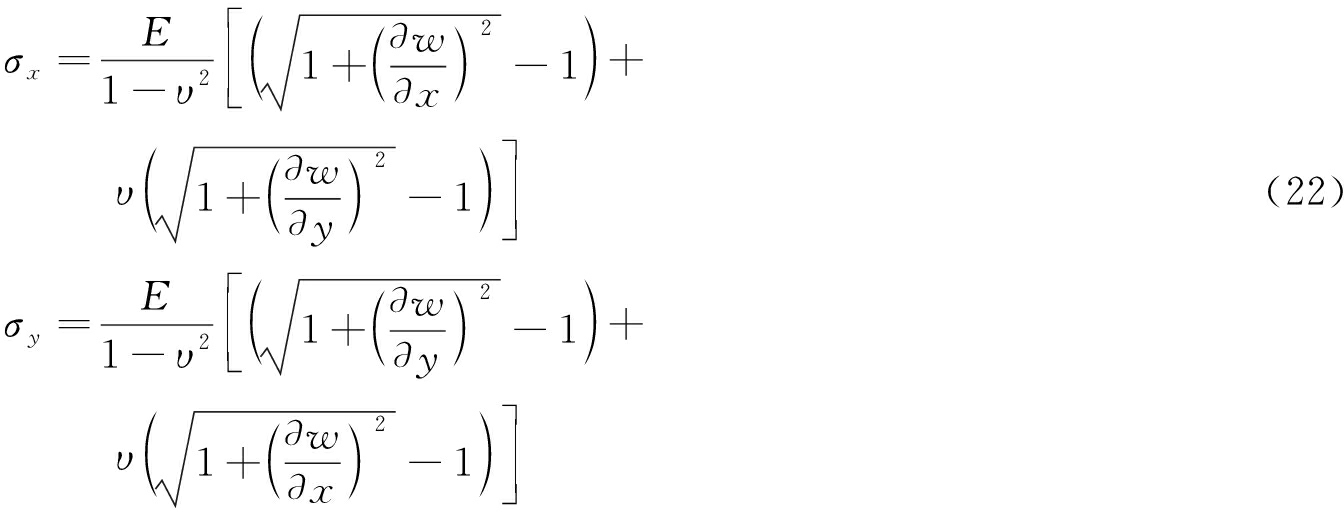
(23)
在此基础上可以分别求出弹性薄板在x轴和y轴方向上拉应力σx和σy,并与岩体的抗拉强度进行比较最终得到岩体破坏准则:当Max[σx,σy]<βσu时,岩体保持稳定状态;当Max[σx,σy]= βσu时,岩体正处于破坏与稳定的临界值;当Max[σx,σy]>βσu时,岩体发生破坏。若σx和σy中只有σx大于βσu,则顶板中的裂隙沿y轴方向扩展;若σx和σy中只有σy大于βσu,则顶板中的裂隙沿x轴方向扩展;若σx和σy均大于βσu,则顶板中的裂隙沿与σx和σy合力垂直的方向扩展,此时对应的a为直接顶初次垮落步距,对应的x和y的值为顶板最先发生破坏的位置。
4.2 初次破断分析
自开切眼到工作面“顶板侧”岩层顶板初次破断前,工作面“顶板侧”岩层顶板可以看成是四周固支板模型,通过之前的分析可以将直接顶的法向应力简化成均布载荷,即P(x,y)=p,因此直接顶在初次破断前的挠度方程的待定系数Amn可以表示为
(24)
式中,p为作用在弹性薄板上的均布载荷。
将均布载荷作用下求解的挠度方程待定系数式(24)带入式(13)并进一步带入到弹性薄板拉应力与薄板挠度的关系式(22)和(23)中,最终获得直接顶不同位置不同方向的拉应力分布方程:
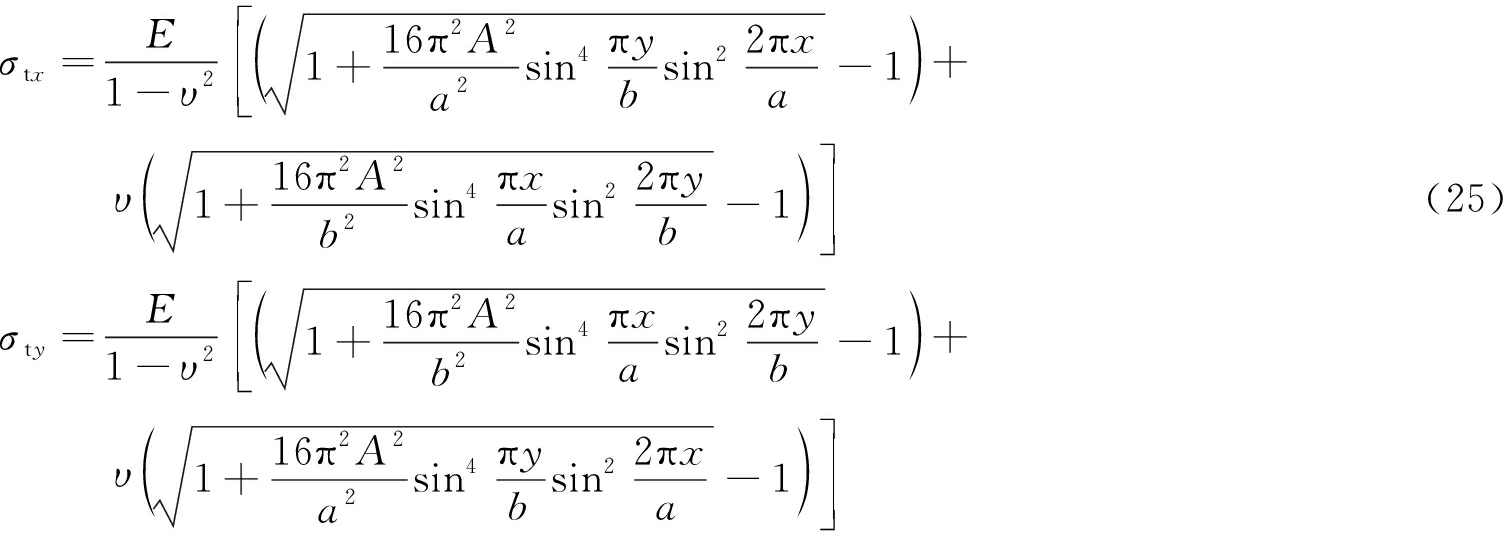
(26)
式中,σtx和σty分别是岩层倾斜方向和走向方向上的拉应力。
假设直接顶在初次破坏前是连续的均匀的,在固定的区间内存在极值,通过计算可知
当x=0.352 4a(或0.647 6a),且![]() 取最大值,即
取最大值,即
(27)
当![]() 且y=0.352 4b(或0.647 6b)时,σty取最大值,即
且y=0.352 4b(或0.647 6b)时,σty取最大值,即
(28)
实际工程应用过程中,直接顶岩层泊松比υ,岩层倾角θ、分段高度bsinθ、弹性模量E和直接顶的法向应力均可以看成常数,因此可以获得工作面不同推进距离a与直接顶不同方向上的最大拉应力σtxmax和σtymax。与此同时,直接顶岩石抗拉强度σu和强度折减系数β也可通过实验室和现场声波测试获得,将理论计算获得的直接顶最大拉应力与试验获得的岩石最大拉应力进行对比分析,依据上文所建立的岩层破坏准则对直接顶稳定性进行判别,当直接顶内部拉应力达到岩体抗拉强度时,直接顶将会在拉应力最大处发生张拉破坏,直接顶内部裂隙扩展的方向与拉应力方向垂直,对应的工作面推进距离a即为直接顶岩层初次垮断步距。
5 结 论
(1)根据近直立特厚煤层分段开采过程中,直接顶初次破坏前的应力特征,建立了直接顶初次破断前的薄板力学模型,并求出对应的挠度方程。
(2)用正交设计的方法对近直立煤层水平分段开采过程中的顶板应力分布情况进行模拟,通过分析确定多种参数对直接顶法向应力影响权重,在去除边缘效应区后,可以认为顶板的法向应力为均布载荷。
(3)应用广义胡克定律和最大拉应力强度准则得出了直接顶拉应力的最大值及其所处的位置,直接顶内部裂隙发生的位置及其扩展方向。
参考文献(References):
[1] 杨孟达.煤矿地质学[M].北京:煤炭工业出版社,2006.
[2] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010.
[3] 张勇,吴健.放顶煤开采顶煤的裂移度及顶煤可放性[J].中国矿业大学学报,2000,29(5):64-67,72.
ZHANG Yong,WU Jian.Crack-movement degree and caving characteristic of top-coal in longwall top-coal caving mining[J].Journal of China University of Mining and Technology,2000,29(5):64-67,72.
[4] 张勇,司艳龙,石亮,等.大截深综放对含硬煤散体顶煤放出率的影响[J].煤炭学报,2011,36(S1):1-6.
ZHANG Yong,SI Yanlong,SHI Liang,et al.The influence of large cut fully-mechanized top-coal caving on recovery rate of granular top-caol mixed with inter-band hard coal[J].Journal of China Coal Society,2011,36(S1):1-6.
[5] 张勇,司艳龙,石亮.块度对顶煤放出率影响的数值模拟分析[J].采矿与安全工程学报,2011,28(2):247-251.
ZHANG Yong,SI Yanlong,SHI Liang.Numerical simulation of the effect of particle size on coal caving ratio[J].Journal of Mining and Safety Engineering,2011,28(2):247-251.
[6] 张勇,张保,李立,等.急倾斜综放开采顶板裂隙发育规律对瓦斯抽采影响研究[J].采矿与安全工程学报,2014,31(5):809-813.
ZHANG Yong,ZHANG Bao,LI Li,et al.Study on the effect of roof fracture development on gas draing in steep full-mechanized caving ming[J].Journal of Mining and Safety Engineering,2014,31(5):809-813.
[7] 张宏伟,荣海,陈建强,等.基于地质动力区划的近直立特厚煤层冲击地压危险性评价[J].煤炭学报,2015,40(12):2755-2762.
ZHANG Hongwei,RONG Hai,CHEN Jianqiang,et al.Risk assessment of rockburst based on geo-dynamic division method in suberect and extremely thick coal seam[J].Journal of China Coal Society,2015,40(12):2755-2762.
[8] 张宏伟,荣海,陈建强,等.近直立特厚煤层冲击地压的地质动力条件评价[J].中国矿业大学学报,2015,44(6):1053-1060.
ZHANG Hongwei,RONG Hai,CHEN Jianqiang,et al.Geo-dynamic condition evaluation method for rockburst in suberect and extremely thick coal[J].Journal of China university of Mining and technology,2015,44(6):1053-1060.
[9] 王宁波,张农,崔峰,等.急倾斜特厚煤层综放工作面采场运移与巷道围岩破裂特征[J].煤炭学报,2013,38(8):1312-1318.
WANG Ningbo,ZHANG Nong,CUI Feng,et al.Characteristics of stope migtation and roadway surrounding rock fracture for full-mechanized top-coal caving face in steeply dipping and extra-thick coal seam[J].Journal of China Coal Society,2013,38(8):1312-1318.
[10] 屠洪盛,屠世浩,陈芳,等.基于薄板理论的急倾斜工作面顶板初次变形破断特征研究[J].采矿与安全工程学报,2014,31(1):49-54,59.
TU Hongsheng,TU Shihao,CHEN Fang,et al.Study on the defection and fracture feature of steep inclined coal seam roof based on the theory of thin plates[J].Journal of Mining and Safety Engineering,2014,31(1):49-54,59.
[11] 杜锋,白海波.薄基岩综放采场直接顶结构力学模型分析[J].煤炭学报,2013,38(8):1331-1337.
DU Feng,BAI Haibo.Mechanical analysis of immediate roof in fully mechanized top coal mining with thin bedrook[J].Journal of China Coal Society,2013,38(8):1331-1337.
[12] 高峰,钱鸣高,缪协兴.老顶给定变形下直接顶受力变形分析[J].岩石力学与工程学报,2000,19(2):145-148.
GAO Feng,QIAN Mianggao,MIAO Xiexing.Mechanical analysis of the immediately roof subjected to given defection of the main roof[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(2):145-148.
[13] 张自政,柏建彪,王卫军,等.沿空留巷充填区域直接顶受力状态探讨与应用[J].煤炭学报,2017,42(8):1960-1970.
ZHANG Zizheng,BAI Jianbiao,WANG Weijun,et al.Study on stress of immediately roof above back fill area in gob side entry retain and its application[J].Journal of China Coal Society,2017,42(8):1960-1970.
[14] 蔡峰,苗沛沛,王二雨,等.厚层灰岩直接顶沿空成巷切顶断裂条件及围岩移动规律研究[J].采矿与安全工程学报,2017,34(3):488-494.
CAI Feng,MIAO Peipei,WANG Eryu,et al.Fracture condition and moving rule of surround rocks in the joint cutting immediate roof of thick-layer limestone[J].Journal of Mining and Safety Engineering,2017,34(3):488-494.
[15] MAGRAB E B.Vibrations of elastic systems.Solid mechanics and its applications[M].Dordrecht:Springer,2012,184:340-344.
[16] KHARAGHANI H.Arrays for orthogonal designs[J].Journal of Combinatorial Designs,2000,8(3):166-173.
[17] HELCIO Vieira J,SUSAN Sanchez,KARL Heinz Kienitz,et al.Generating and improving orthogonal designs by using mixed integer programming[J].European Journal of Operational Research,2011,215(3):629-638.
[18] WU Aixiang,HUANG Mingqing,HAN Bin.Orthogonal design and numerical simulation of room and pillar configurations in fractured stopes[J].Journal of Central South University,2014,21(8):3338-3344.
[19] BRADY B H G,BROWN E T.Rock mechanics for underground mining (third edition)[M].Dordrecht:Springer,2006:142-161.
[20] 孙训方,方孝淑,关来泰.材料力学(第五版)[M].北京:高等教育出版社,2009:216-217.
[21] 李维红.脆性材料的亚临界裂纹扩展和双向应力影响的数值模拟[J].稀有金属材料与工程,2009,38(S2):1112-1116.
LI Weihong.Numerical simulation of subcritical crack growth in brittle materials and influence of biaxial stress[J].Rare Metal Materials And Engineering,2009,38(S2):1112-1116.
[22] 许昭永,王彬,胡毅力,等.试论岩石破裂和破坏的差异对地震模拟及前兆研究的影响[J].地球物理学报,2009,52(3):712-719.
XU Zhaoyong,WANG Bin,HU Yili,et al.A discussion on the influence of the different between the rock fracture and failure to the earthquake simulation and the precursor studies[J].Chinese Journal of Geophysics,2009,52(3):712-719.