液固分选流化床(Liquid Solid Fluidized Bed Separator,LSFBS)由于分选效果好,分选密度范围广以及易于实现自动化等优点,已广泛用于粗煤泥分选、细粒金属矿粗选以及电路板等废弃资源回收[1-4]。颗粒在自生的密相液固流化床层内按密度差异分离是LSFBS的分选特征,液固流化床层内颗粒干扰沉降速度的大小决定了颗粒的最终去向。
颗粒干扰沉降末速与颗粒粒度、密度正相关,与流化床中颗粒体积分数负相关。前人对颗粒干扰沉降进行了大量研究,并得到相应的干扰沉降末速公式[5-10],这些模型都能正确反映上述颗粒干扰沉降速度随颗粒性质和颗粒体积分数的变化规律。根据干扰沉降末速模型建立方法,可将干扰沉降末速模型分为理论和经验两大类。干扰沉降末速理论模型一般基于颗粒受力导出;而经验模型则通过试验获得。
本文将液固流化床层等效为一种准流体,根据颗粒边界层所受流体阻力推导干扰沉降末速,通过颗粒流化试验结果验证了模型的准确性。
1 颗粒干扰沉降末速模型的建立
1.1 液固流化床层内颗粒间相互作用的近似处理
当颗粒在某一流化速度下形成稳定床层后,床层内颗粒还存在一些循环流动,最显著的就是颗粒由床层中心区向上,再由两侧近壁面低速区向下的循环运动。但从床层整体来看,床层平均空隙率和平均密度随时间不再改变,所有颗粒与壁面的相对速度平均值为零。因此,可以认为颗粒此时受力达到平衡,床层空隙里的液体流态可近似为均匀定常流。此时,颗粒所受横向升力、Basset力、压力梯度力和虚拟质量力都为0。由此,建立颗粒受力平衡方程为
![]()
(1)
式中,ρP,dP,分别为颗粒的密度、粒度;A为颗粒迎流横截面积;up为颗粒速度;uF为流体介质的速度;CD为流体阻力系数;ρeff为准流体有效密度,最后一项为某时刻周围所有颗粒对目标颗粒作用之和。
干扰沉降条件形成后,周围颗粒对目标颗粒运动影响体现在两方面,即周围颗粒的存在改变了目标颗粒周围流场,导致颗粒所受与速度梯度和压力梯度相关的作用力发生变化;其次,由于颗粒体积分数增大,目标颗粒与周围颗粒碰撞概率显著增大,碰撞作用将直接改变颗粒运动轨迹。这两方面作用导致颗粒沉降过程中所受阻力增大,进而导致干扰沉降末速大大降低。GIBILARO等[11]将液固悬浮液类比为准流体,研究了液固悬浮液相关性质随颗粒体积分数变化规律。本文亦采用该方法,把自生密相液固流化床层看作一种准流体,如图1所示,将自生密相液固流化床层内颗粒间相互作用以准流体有效密度和表观黏度的概念来体现。
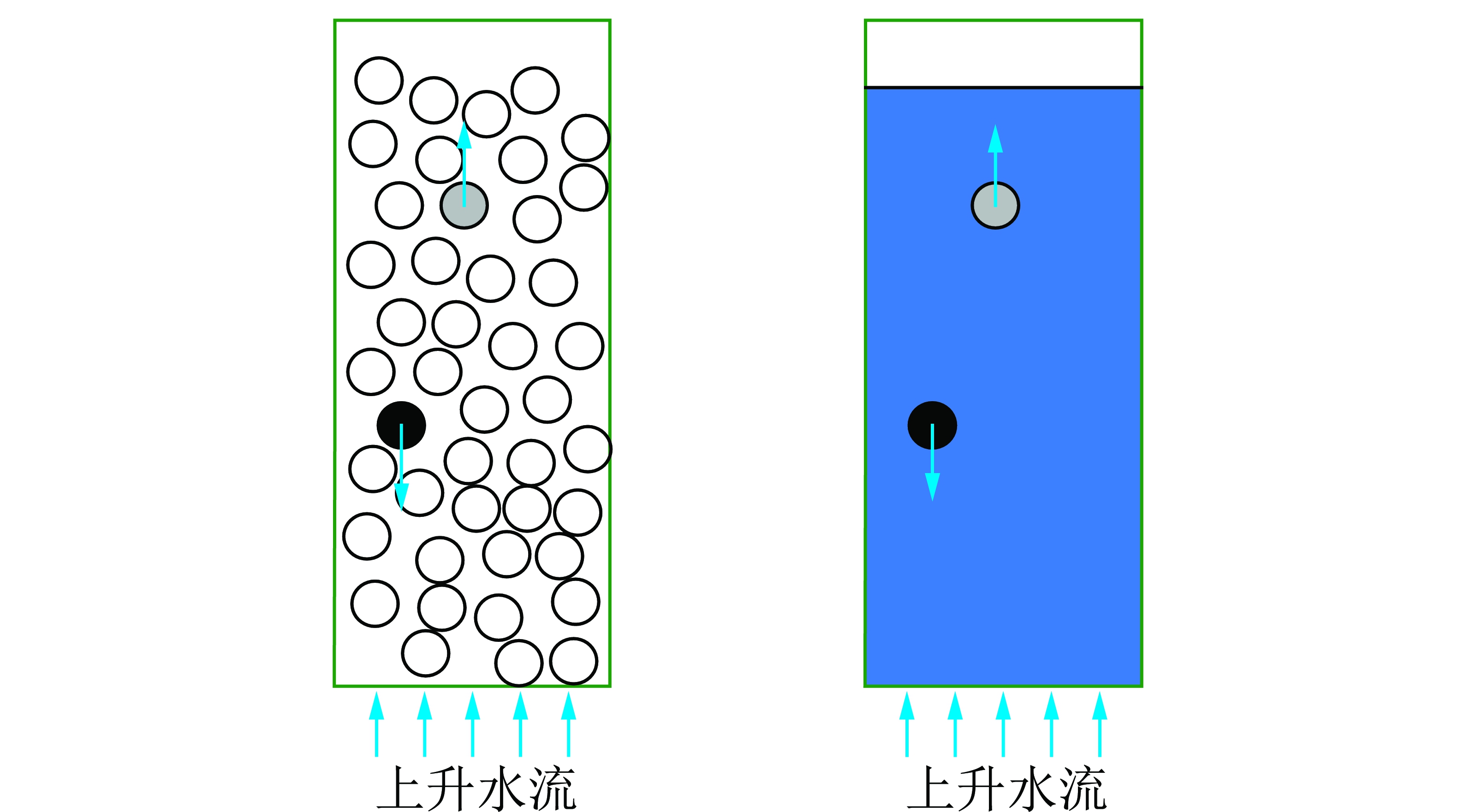
图1 准流体法简化流化床层
Fig.1 Simplification of liquid-solid fluidized bed by using pseudo-fluid analogy
ρeff按下式计算:
(2)
式中,m′和n′分别为入料颗粒的密度级数量和粒度级数量;φij为粒度为i,密度为j的颗粒体积分数;ρF为流体介质的密度。
EINSTEIN,BARNEA & MIZRAHI,GIBILARO,SWANSON和BROUWER等分别给出了液固悬浮液表观黏度计算公式,其中SWANSON公式不仅引进了颗粒最大堆积体积分数φmax,有效避免了悬浮液中颗粒体积分数接近最大堆积体积分数时计算误差过大的问题,其数学形式也相对简单,因此本文中准流体表观黏度则根据SWANSON[12]的半经验公式计算:
(3)
式中,φ为颗粒体积分数。
1.2 颗粒干扰沉降末速数学模型的建立
黏性流体流过物体时,物体受到的阻力由两部分组成:摩擦阻力和压差阻力。压差阻力的产生与边界层分离现象密切相关。根据量纲分析,颗粒表面某点对应的边界层厚度δ与颗粒雷诺数有以下关系:
(4)
式中,L为外势流区长度尺度,对于LSFBS内颗粒边界层,L近似为颗粒直径。
颗粒边界层内,压力沿法向不变,即
(5)
因此颗粒表面的流速和压力分布即为边界层边界上的速度和压力分布。对于均匀稳定的液固流化床,颗粒表面某点处所受压力与床层高度的关系可表示为
(6)
式中,右侧第1项为此深度处水的静压,第2项为目标颗粒周围其他颗粒沉降运动时因自身有效重力转移到周围流体产生的。
根据ABRAHAM[13]的研究结果,得到边界层分离点处,边界层厚度与颗粒雷诺数关系为
(7)
根据颗粒表面边界层厚度和压力分布,对边界层压力沿边界层外边界积分,同时结合式(7),得到颗粒所受流体阻力[14-15]为
(8)
式中,C0=0.28,为根据颗粒表面边界层压力分布求得的参数,与边界层分离点处压力有关。
根据阻力系数的定义,由式(8)得阻力系数为
(9)
式(9)中颗粒雷诺数亦采用准流体相关物性计算。略去式(1)左端最后一项,同时用准流体有效密度ρeff和表观黏度μeff分别替换式中ρF和μF以体现颗粒间作用,整理得到液固流化床内颗粒受力平衡时,流体阻力系数为
(10)
借鉴Concha和Almendra的处理方法[11],令式(9)和(10)相等,并将ReP代入,最后得到液固流化床层内颗粒干扰沉降末速公式为
(11)
式中,![]()
2 液固流化床层内颗粒干扰沉降末速数学模型的验证
2.1 颗粒物性和流化试验系统
搭建了颗粒流化试验系统如图2所示,其中A表示上升水流旁路调节阀,B表示主上升水流阀,C表示副上升水流阀(微调阀门),D表示小量程涡轮流量计,E大量程涡轮流量计,F表示溢流回水管,G表示溢流收集槽,H表示清水池,I表示离心泵,J表示底流桶,K表示溢流水缓冲池,L表示溢流脱水筛,M表示压力传感器,N表示流化颗粒(此处为不同粒度的石英砂)。上升水流由平行管流体分布器射出后,在液固流化床柱体内向上流动并沿径向逐渐均匀分布,经第1层0.045 mm筛网后,流体径向速度基本实现均匀。待流化颗粒放置于第2层筛网上,第2层筛网孔径也为0.045 mm,以得到均匀稳定的液固流化床层,同时筛孔远小于待流化颗粒粒径,保证底层颗粒受到较均匀向上的流体曳力,且不会沿近壁面区漏下。
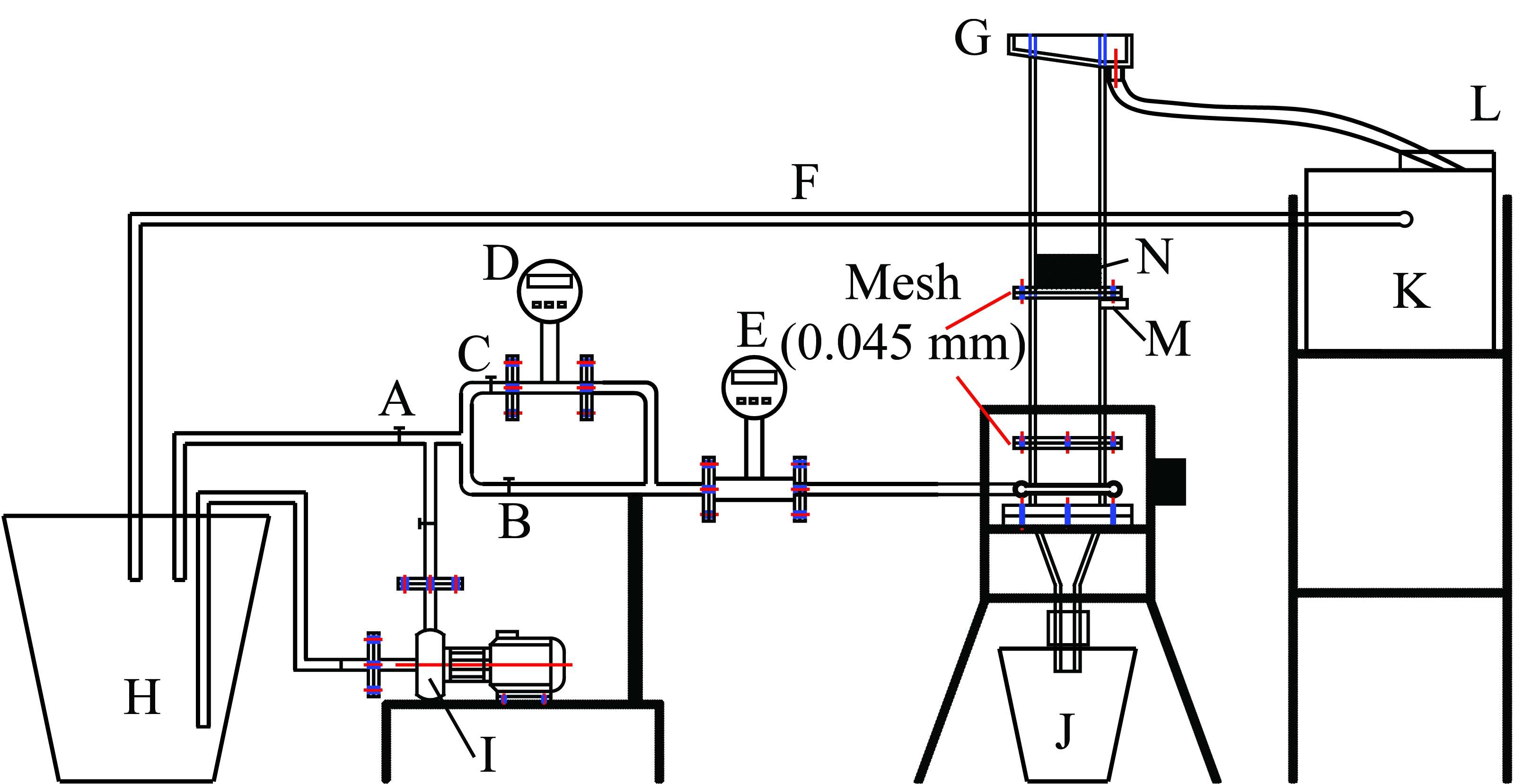
图2 液固流化试验系统
Fig.2 Experiment system for liquid-solid fluidization
为精确显示和控制上升水流流量,给水管流量测量采用精度较高的涡轮流量计;对于不同密度、粒度颗粒流化的表观上升水流速度相差较大,因此,设计了如图2所示的上升水流管路。其工作原理是:当待流化颗粒粒度或密度较低时,关闭主上升水流阀,此时上升水流只能通过副上升水流阀(副上升水流阀是一个微调阀门,保证上升水流的精确控制),流经小量程的涡轮流量计;当待流化颗粒粒度或密度较大时,则同时开启主副上升水流阀,先调节主上升水流阀使上升水流处于某一范围内,再调节副上升水流阀,每次调节并稳定后,观察上升水流流量,达到预设值后,再观察并测量床层相关性质;通过床层的水流经筛孔为0.045 mm的漏桶过滤后,先给到溢流缓冲池,再经管路返回至离心泵蓄水池,如此来回收带出颗粒和实现水流循环利用。
准备一定质量的粒度分别为0.25~0.35和0.63~0.75 mm煤粒以及粒度分别为0.25~0.35和0.50~0.63 mm石英砂颗粒作为流化颗粒。4种流化颗粒相关性质及4种颗粒构成的初始床层性质见表1,其中,H0为粒群在完全流化时突然让上升水流速度为0,待颗粒在水中自由沉降完成后,在第2层筛网上形成的固体颗粒床层的初始高度,φ0则为此时固体颗粒床层对应的固体体积分数。通过比重瓶测出各组颗粒的真实密度。利用比重杯测出一定体积V下颗粒达到最密堆积时的质量MP,根据下式计算出各组颗粒最大堆积体积分数:
表1 流化颗粒性质
Table 1 Properties of the fluidized particles

(12)
2.2 颗粒干扰沉降末速数学模型的验证
稳定流化床层形成后,某一时刻,床层内所有颗粒相对壁面的平均速度为0,因此,对于整个床层来讲,此时床层内部所有颗粒整体上达到了相应颗粒体积分数下的干扰沉降末速,根据颗粒体积分数与流化速度得到此时颗粒干扰沉降末速为
(13)
令H为上升水流速度为uF时颗粒床层高度,则此时液固流化床层内颗粒平均体积分数为
(14)
根据流化试验中不同上升水流速度下床层高度以及式(14)得到颗粒干扰沉降末速随颗粒体积分数变化规律如图3所示。
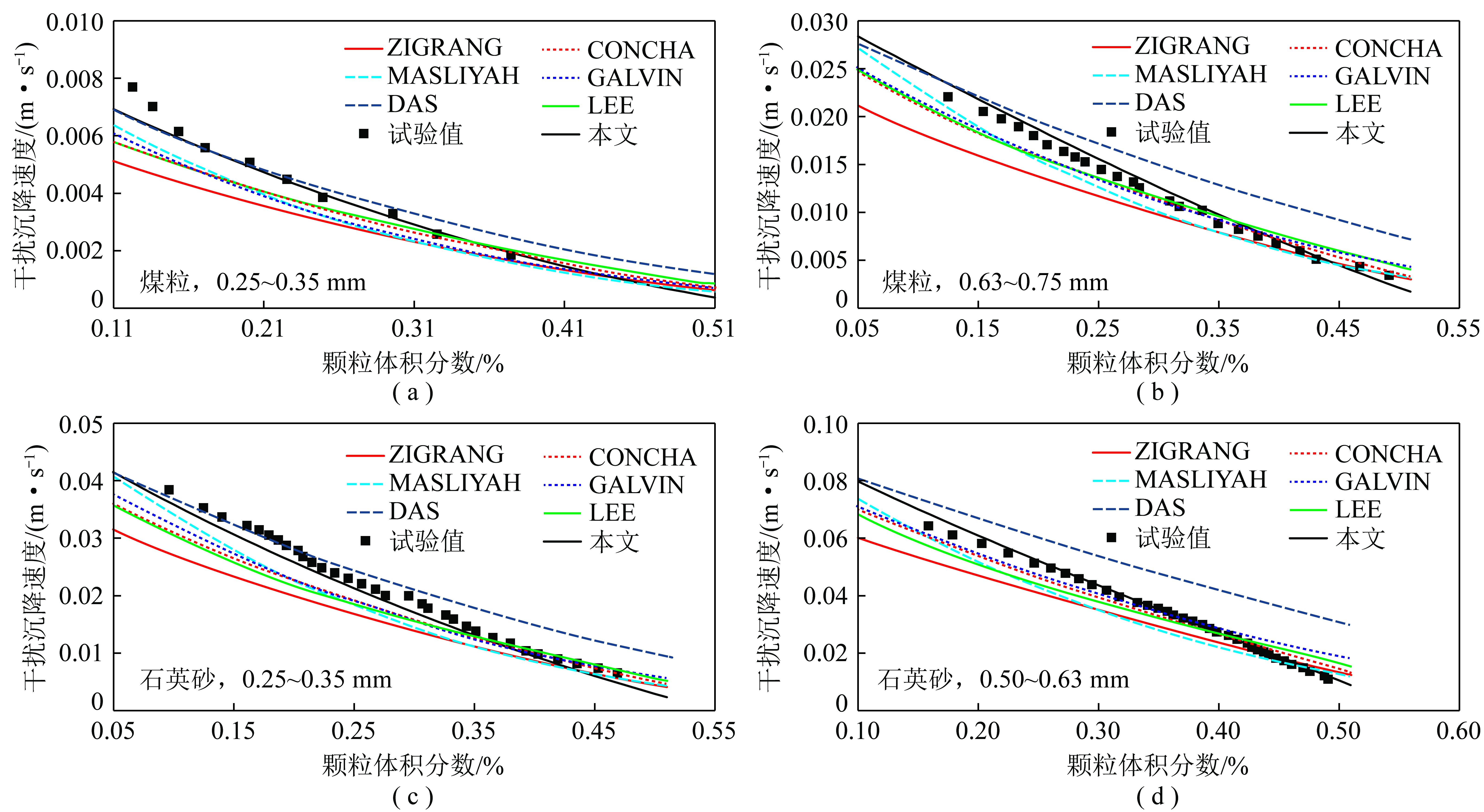
图3 各模型预测4种颗粒干扰沉降末速对比
Fig.3 Comparison of predicted hindered settling velocities of four kind of particles
前人对干扰沉降现象进行了大量研究,其中ZIGRANG & SYLVESTER[16],GALVIN & NGUYENTRANLAM[17],CONCHA-ALMENDRA[20],MASLIYAH[19],LEE[18],DAS[21]等的干扰沉降末速模型较为常见,预测结果较好,对应的数学形式分别式(15)~(20)所示,其中LEE模型是借鉴CONCHA-ALMENDRA方法推导出来的,因此形式与CONCHA-ALMENDRA模型相近。
(15)
![]()
(16)
式中,ρb为流化床层表观密度。
(17)
P=1+0.092 1![]() 1/2f2(φ)
1/2f2(φ)
![]()
(18)
式中,ε为液固流化床层空隙率,ε=1-φ;F(ε)为液固流化床孔隙率以及颗粒雷诺数的函数,F(ε)=(1-φ)n,n与RICHARDSON和ZAKI公式中的n相同。
(19)
DAS模型采用RICHARDSON & ZAKI模型形式,差异在于公式中n值和颗粒自由沉降末速U0的计算方法:
(20)
其中,n值按ROWE公式计算,U0计算方法可查阅相关文献[17]。
将以上6个模型预测值以及本文模型预测值与4种颗粒不同体积分数下的干扰沉降速度试验值进行对比(图3)。由图3可知,各模型基本都能正确反映4种颗粒干扰沉降末速随颗粒体积分数变化规律,其中本文模型预测值的准确度明显高于其他模型。
将颗粒干扰沉降末速的模型预测值和试验值与相应颗粒自由沉降末速做比,进行无量纲化(图4)。
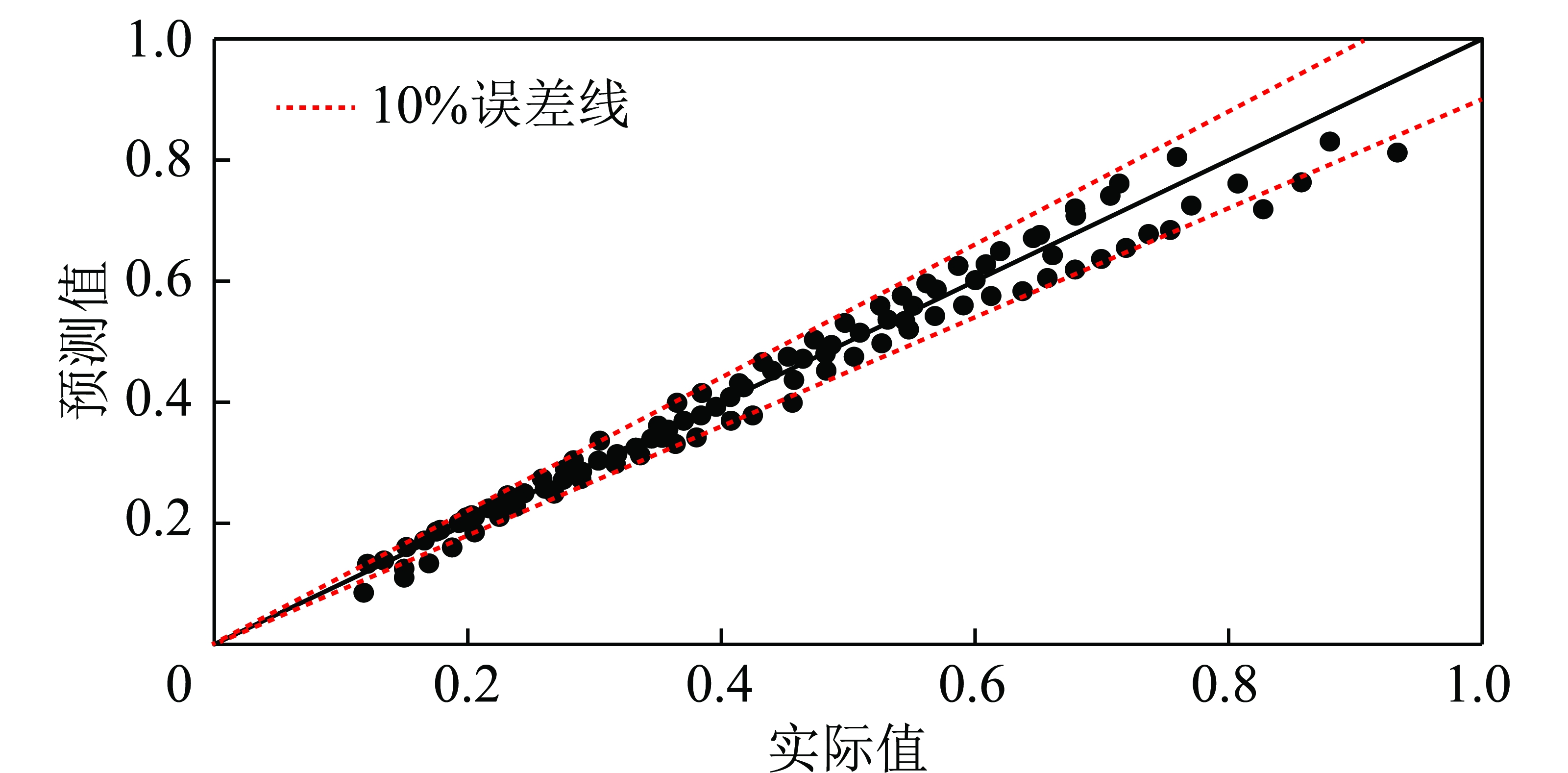
图4 无量纲化后预测值与试验值对比
Fig.4 Comparison between predicted and experimental value after nondimensionalization
颗粒自由沉降末速[16,22]按下式计算:
![]()
(21)
以无量纲化后的试验值为横坐标,相应预测值为纵坐标,做出本文模型4种颗粒干扰沉降末速预测值的误差分布,可知,本文模型预测值基本都位于相对误差10%以内,证明了本文干扰沉降末速模型准确度较高。
利用本文提出的干扰沉降末速模型预测密度分别为1 300和2 200 kg/m3两种颗粒等沉比,假设流化床层内两种颗粒体积分数相同,且低密度颗粒粒度为1 mm,求得两种密度颗粒等沉比及达到等沉时高密度颗粒粒度随床层内颗粒体积分数变化情况如图5所示。由图5可知,随颗粒体积分数增大,两颗粒等沉比逐渐增大,而对应的高密度颗粒粒度逐渐减小;颗粒体积分数越大,等沉比随颗粒体积分数增大速度或高密度颗粒粒度随颗粒体积分数减小速度也越大;当颗粒体积分数为0.35时,等沉比达到5.38,对应高密度颗粒粒度为0.186 mm,表明液固流化床层内,颗粒体积分数越大,允许的入料粒度上下限之比越大,越易实现较高的分选效率。由于床层内颗粒体积分数与上升水流速度呈负相关,当入料粒度上限一定时,限制上升水流速度在较低的范围内可减少高密度细粒对溢流的污染,降低粒度效应对重选过程的影响。

图5 颗粒等沉比随颗粒体积分数变化趋势
Fig.5 Influence of particles volume fraction on equal settling ratio
3 结 论
(1)采用将液固流化床层类比为准流体,以准流体有效密度和表观黏度概念体现颗粒间相互作用,结合边界层理论推导了液固流化床内颗粒干扰沉降末速数学模型,其中准流体表观黏度采用SWANSON的半经验公式计算。
(2)建立了颗粒流化-沉降试验系统,得到了颗粒干扰沉降速度随颗粒体积分数变化规律,用颗粒干扰沉降末速试验值比较了不同干扰沉降末速数学模型的预测精度,发现本文模型预测值准确度明显高于其他模型,4种颗粒不同体积分数下干扰沉降末速预测值的相对误差基本可控制在10%以内。
(3)利用干扰沉降末速模型探究了等沉比随流化床颗粒体积分数的变化规律,发现颗粒体积分数越大,两种密度颗粒等沉比越大;在低上升水流速度和高颗粒体积分数条件下,可减少高密度细粒对液固分选流化床溢流的污染,一定程度上抑制粒度效应对分选过程的影响。
参考文献(References):
[1] VENUGOPAL R,PATEL J P,BHAR C.Coal washing scenario in India and future prospects[J].International Journal of Coal Science & Technology,2016,3(2):1-7.
[2] 孙铭阳,韦鲁滨,朱学帅,等.液固分选流化床三相流场模拟中各粘性流动模型的适用性[J].过程工程学报,2016,16(1):10-17.
SUN Mingyang,WEI Lubin,ZHU Xueshuai,et al.Research on performances of different viscous models in simulation of three-phase flow fields in a liquid-solid fluidized bed separator[J].The Chinese Journal of Process Engineering,2016,16(1):10-17.
[3] 张迟强,李延锋,陈文刊,等.加重介液固流化床分选宽粒级粗煤泥的试验研究[J].煤炭工程,2016,48(5):122-125.
ZHANG Chiqiang,LI Yanfeng,CHEN Wenkan,et al.Experiment study on wide-size-fraction coarse slime separation with dense mediun liquid solid fluidized bed[J].Coal Engineering,2016,48(5):122-125.
[4] 胡林,伍玲玲,喻清,等.充气式液固流化床内颗粒运动研究[J].矿山机械,2016(9):62-65.
HU Lin,WU Lingling,YU Qing,et al.Research on particle motion in aerated liquid-solid fluidized bed[J].Mining & Processing Equipment,2016(9):62-65.
[5] ARABI A S,SANDERS R S.Particle terminal settling velocities in non-Newtonian viscoplastic fluids[J].Canadian Journal of Chemical Engineering,2016,94(6):1092-1101.
[6] LI W,YANG S,HU J,et al.Field measurements of settling velocities of fine sediments in Three Gorges Reservoir using ADV[J].International Journal of Sediment Research,2016,31(3):237-243.
[7] SUN M,WEI L,CUI G.Studies of a water-only cyclone with a three-stage cone for fine coal beneficiation[J].International Journal of Coal Preparation & Utilization,2017,37(2):75-86.
[8] LOCKETT M J,AL-HABBOOBY H M.Differential settling by size of two particle species in a liquid[J].Trans.Inst.Chem.Eng.,1973,51(2):281-292.
[9] BRAUER H,THIELE H.Bewegung von partikel-schwarmen[J].Chen.Ing.Tech.,1973,45(13):909-912.
[10] SMITH T N.A model of settling velocity[J].Chemical Engineering Science,1998,53(2):315-323.
[11] GIBILARO L G,GALLUCCI K,FELICE R D,et al.On the apparent viscosity of a fluidized bed[J].Chemical Engineering Science,2007,62(1-2):294-300.
[12] SWANSON V F.Free and hindered settling[J].Minerals and Metallurgical Processing,1989(11):190-196.
[13] ABRAHAM F F.Functional dependence of drag coefficient of a sphere on reynolds number[J].Physics of Fluids,1970,13:2194-2195.
[14] CONCHA F,ALMENDRA E R.Settling velocities of particulate systems,2.Settling velocities of suspensions of spherical particles[J].International Journal of Mineral Processing,1979,6(1):31-41.
[15] BARNEA E,MIZRAHI J.A generalized approach to the fluid dynamics of particulate systems:Part 1.General correlation for fluidization and sedimentation in solid multiparticle systems[J].Chemical Engineering Journal,1973,5(2):171-189.
[16] ZIGRANG D J,SYLVESTER N D.An explicit equation for particle settling velocities in solid-liquid systems[J].AICHE Journal,1981,27(6):1043-1044.
[17] GALVIN K P,PRATTEN S,NGUYEN Tran Lam G.A generalized empirical description for particle slip velocities in liquid fluidized beds[J].Chemical Engineering Science,1999,54(8):1045-1052.
[18] H L C.Modeling of batch hindered settling[D].Pennsylvania:The Pennsylvania State University,1989.
[19] MASLIYAH J H.Hindered settling in a multi-species particle system[J].Chemical Engineering Science,1979,34(9):1166-1168.
[20] CONCHA F,ALMENDRA E R.Settling velocities of particulate systems,2.Settling velocity of suspension of spherical particles[J].International Journal of Mineral Processing,1979,6:31-41.
[21] DAS A,SARKAR B,MEHROTRA S P.Prediction of separation performance of floatex density separator for processing of fine coal particles[J].International Journal of Mineral Processing,2009,91(1-2):41-49.
[22] GALVIN K P,DOROODCHI E,CALLEN A M,et al.Pilot plant trial of the reflux classifier[J].Minerals Engineering,2002,15(1-2):19-25.