
王凤云1,2,钱德玲1
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽建筑大学 土木工程学院,安徽 合肥 230022)
摘 要:为研究中间主应力在圆形隧道围岩承载力所发挥的作用,根据统一强度理论和塑性增量的非相关性流动法则,提出了考虑中间主应力影响的应变软化围岩特征曲线的有限差分计算方法,并通过实例验证该方法的正确性。由于围岩的力学模型对特征曲线的影响较大,采用3种不同力学模型——弹塑性模型、弹脆性模型和应变软化模型,分别研究了中间主应力和支护力对圆形隧道围岩塑性区半径,应力分布和隧道洞壁处位移的影响。结果表明:当围岩采用弹塑性模型时,计算的塑性区半径和洞壁处的位移均较小,没有考虑岩体强度在塑性区的弱化,建议慎重选择;中间主应力对塑性区半径和洞壁处的位移发展均有抑制作用,特别是在无支护状态下弹脆性模型的抑制作用最显著;中间主应力对塑性发展的抑制作用随着支护力的增加而减小;弹塑性交界处围压,应变软化模型下软化区与残余区交界面的围压均与支护力无关,且随中间主应力影响系数的增加而减小。
关键词:隧道;统一强度理论;中间主应力;塑性区半径;位移

移动阅读
王凤云,钱德玲.考虑中间主应力和软化的圆形隧道围岩弹塑性分析[J].煤炭学报,2018,43(12):3329-3337.doi:10.13225/j.cnki.jccs.2018.0275
WANG Fengyun,QIAN Deling.Elasto-analysis for a deep tunnel considering the intermediate stress and the strain-softening behavior[J].Journal of China Coal Society,2018,43(12):3329-3337.doi:10.13225/j.cnki.jccs.2018.0275
中图分类号:TU452;TD353
文献标志码:A
文章编号:0253-9993(2018)12-3329-09
收稿日期:2018-02-28
修回日期:2018-05-15
责任编辑:常 琛
作者简介:王凤云(1989—),女,安徽无为人,博士研究生。 E-mail:fengyunwang_sc@sina.com
通讯作者:钱德玲(1956—),女,安徽望江人,教授,博士。E-mail:dlqian@sina.com
WANG Fengyun1,2,QIAN Deling1
(1.Scool of Civil and Hydraulic Engineering,Hefei University of Technology,Hefei 230009,China; 2.School of Civil Engineering,Anhui Jianzhu University,Hefei 230022,China)
Abstract:To study the role of the intermediate stress on the bearing capacity in a circular tunnel,a finite difference method,which is used to calculate the strain-softening behavior of rock masses considering the effect of the intermediate stress,is proposed based on unified failure criterion and non-flow associated flue.The accuracy of the proposed method is investigated by example verification.Due to the significant effect of mechanics model on the ground response curve,three different mechanics models,i.e.,elastic-perfect plastic model (EPP),brittle plastic model (BP) and strain-softening model (SS),are used to study the effect of intermediate stress and support force on the plastic radius,the stress distribution in the plastic zone and the displacement at the tunnel wall,respectively.The results show that the plastic radius and the displacement at the tunnel wall calculated by EPP are much less than those by other mechanic models.Therefore,the EPP is suggested to be cautiously used because it does not consider the weakening strength of rock masses in the plastic zone.The intermediate stress can restrain the development of the plastic radius and the displacement at the tunnel wall,especially for EB under no support force condition.This restraining effect of the intermediate stress on the plastic development decreases with the increase of support force.The confining stresses on the boundary of elastic-plastic zone and the boundary of softening-residual zone are not related to support force at the tunnel wall,but decrease with the increase of intermediate stress coefficient.
Key words:tunnels;unified strength theory;intermediate stress;plastic radius;displacement
由于收敛约束法能够综合考虑围岩和支护结构的相互作用,常被学者们用于隧道设计中。收敛约束法主要是由开挖隧道后岩体的特征曲线(GRC),纵向变形曲线(LDP)和支护结构的支护曲线(SCC)3个部分组成[1]。其中GRC反映了支护力和围岩径向位移之间的关系,与LDP存在耦合性,因此,GRC直接影响了收敛约束法在隧道设计中应用。近些年来,大量的研究表明GRC与岩体的峰后力学特性,剪胀性以及岩体的质量密切相关[2-6],但是这些研究都是建立在隧道截面满足平截面假定的基础上,即只考虑最大主应力和最小主应力的作用。在实际中,开挖隧道后的岩体则受到三向主应力的作用,忽略了中间主应力对岩体力学特性的影响,这必然会造成隧道位移计算的偏差,从而影响隧道支护结构的设计。
大量的学者在研究隧道的弹塑性分析时都考虑了中间主应力的影响,如XU等[7]考虑了中间主应力的影响,将YU等[8-9]所提出的统一强度理论运用到圆形隧道计算中;张强等[10]利用统一强度理论分析了中间主应力和弹性模量裂化对圆形隧道解析解的影响;张常光等[11]利用统一强度理论分析了硬脆围岩的自承载能力和隧道围岩稳定变形;CAI[12]从数值模拟的角度研究了中间主应力对岩体强度的影响。以上这些关于中间应力的分析都是基于弹塑性模型假设中,并没有考虑到隧道岩体的强度峰后的力学特性和开挖后硐室的围压变化。根据大量岩体的抗压试验表明[13],质量较好的岩体表现为弹脆性模型,中等级岩体表现为应变软化特性,软岩则近似表现为弹塑性模型,而岩体不同峰后力学特性直接影响了隧道GRC的计算。因此,也需要考虑围岩的峰后力学特性对GRC的影响。
本文提出了考虑中间主应力的应变软化岩体的有限差分计算方法,并验证了该方法的正确性。并分别采用弹塑性模型、弹脆性模型和应变软化模型计算,考虑中间主应力和支护力对开挖后的隧道塑性区半径、塑性区应力分布和GRC的影响。这一研究为深埋圆形隧道的设计及其支护结构的设计提供了更加全面的理论认识。
(1)圆形隧道的岩体为均质材料,均匀受到地应力的作用;
(2)隧道的埋深较深,埋深大于20倍隧道半径;
(3)隧道截面满足平截面假定;
(4)隧道围岩处于静水压力中。
图1为圆形隧道开挖后的3种力学模型,假设岩体为均质材料,受到原地应力为σ0,由于开挖了半径为R0的隧道,形成了半径为R2的塑性区,在弹塑性交界面上的切向和径向应力分别为σθ2和σr2,且硐壁处受到支护结构的支护力pi。当岩体为应变软化材料,且pi小于![]() (软化区与残余区交界处的支护力与此处的围压相等)时,围岩塑性区出现软化区和残余区,所形成的残余区半径为R1,软化区与残余区交界面处的切向和径向应力分别为σθ1和σr1。
(软化区与残余区交界处的支护力与此处的围压相等)时,围岩塑性区出现软化区和残余区,所形成的残余区半径为R1,软化区与残余区交界面处的切向和径向应力分别为σθ1和σr1。
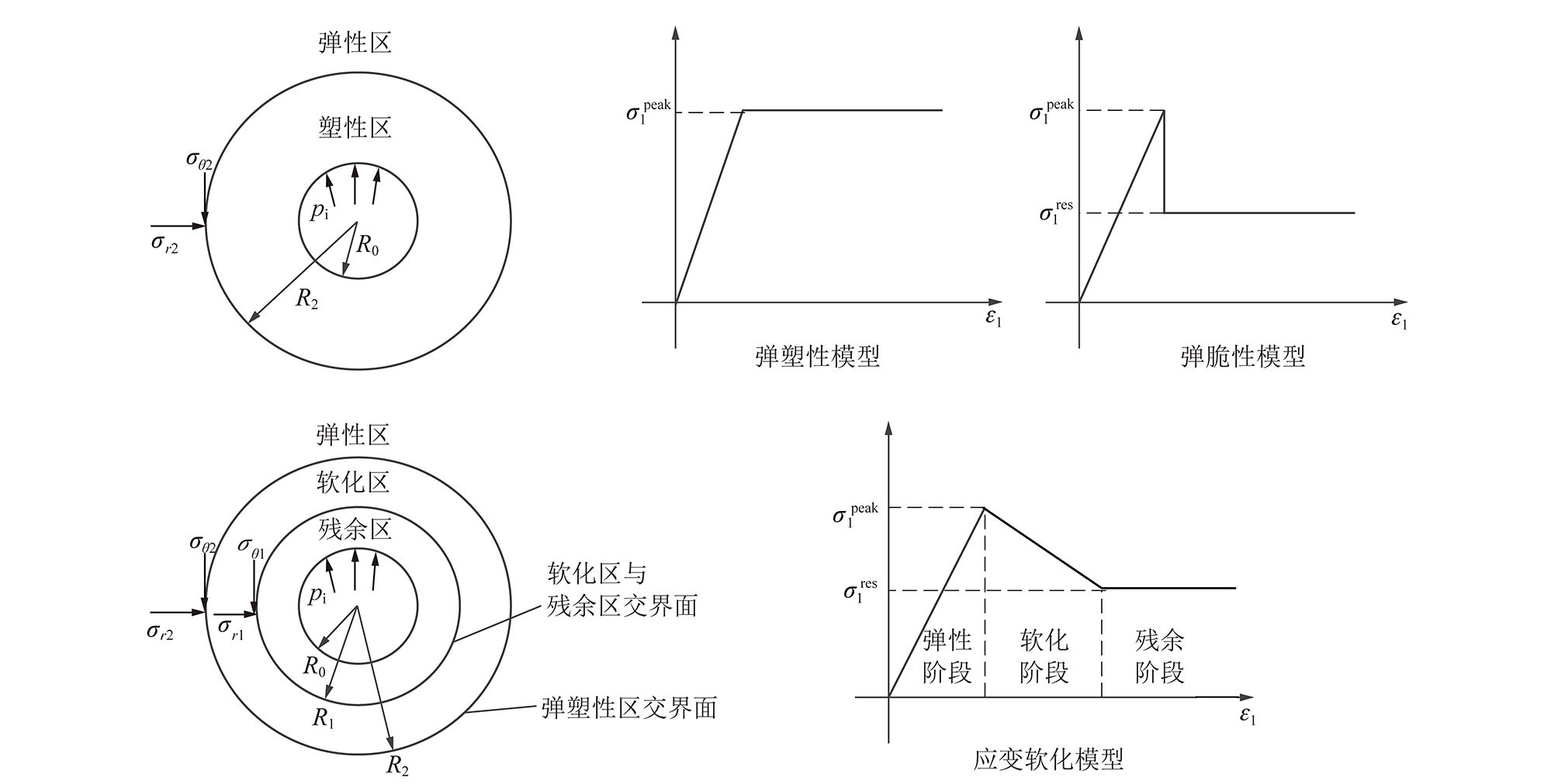
图1 圆形隧道开挖后的3种力学模型
Fig.1 Three kinds of mechanics model for a circular tunnel after excavation
为了考虑3个主应力的综合作用,根据文献[8]中关于统一强度理论的定义,圆形隧道岩体强度满足的计算式如下:
σθ=Kσr+Y
(1)
其中,根据文献[9],取![]() 那么
那么![]() 为中间主应力影响系数,取值范围为0≤b≤1;c和φ为岩体的黏聚力和内摩擦角。
为中间主应力影响系数,取值范围为0≤b≤1;c和φ为岩体的黏聚力和内摩擦角。
需要说明的是,当b=0时,该强度屈服准则退化成Mohr-Coulomb(M-C)准则,当b=1时,该强度屈服准则退化为双剪强度准则。
由图1中应变软化模型的应力应变曲线可知,在一定围压作用下,岩体强度达到峰值后,随着应变的增加,强度逐渐降低直至将至残余值。岩体强度逐渐降低的区域为软化区,降至残余值时则进入残余区。在应变软化模型下,考虑中间主应力的统一强度理论为
σθ=K(η)σr+Y(η)
(2)
式中,K(η)=K(b,φ(η)),Y(η)=Y(b,c(η),φ(η)),η为岩体的塑性软化系数。软化区与残余区交界面处的软化系数为临界软化系数η*,当围岩处于弹性状态时,η=0;当围岩处于软化状态时,0<η<η*;当围岩处于残余状态时,η≥η*。当岩体为弹塑性或弹脆性材料时,η*=0或η*= 。塑性软化系数可以用塑性剪应变表示[14]:
。塑性软化系数可以用塑性剪应变表示[14]:
(3)
其中,![]() 和
和![]() 为切向和径向的塑性应变。在发生塑性变形时,围岩满足Mohr-Coulomb塑性势函数为
为切向和径向的塑性应变。在发生塑性变形时,围岩满足Mohr-Coulomb塑性势函数为
g=σθ-Kψσr
(4)
由非相关性流动法则可知
(5)
式中,![]() 为塑性乘子,
为塑性乘子,![]() 和
和![]() 为围岩的径向和切向塑性应变。
为围岩的径向和切向塑性应变。
将式(4)代入式(5)得到满足非相关性流动法则的关系式:
(6)
其中,Kψ为围岩的剪胀系数,Kψ=(1+sin ψ)/(1-sin ψ),ψ为围岩的剪胀角。假定岩体的强度参数ω(c和φ)在软化区域内线性下降如图2所示,满足下式:
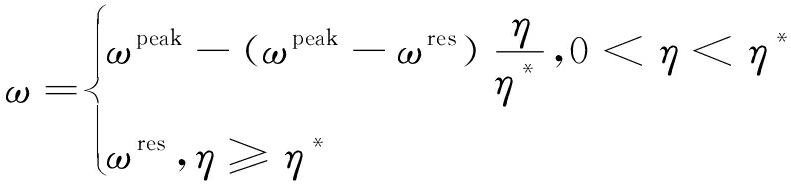
(7)
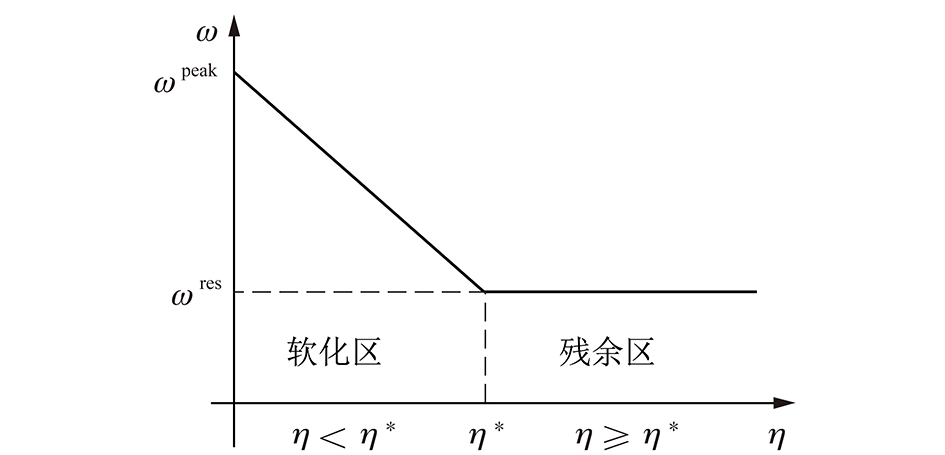
图2 强度参数在塑性区的变化
Fig.2 Variation of strength parameters in the plastic zone
根据平截面假定和力的平衡公式,圆形隧道的σθ和σr满足:
(8)
径向和环向应变εr,εθ:
(9)
由弹性理论可知,弹性区域内的岩体的应力和位移公式为
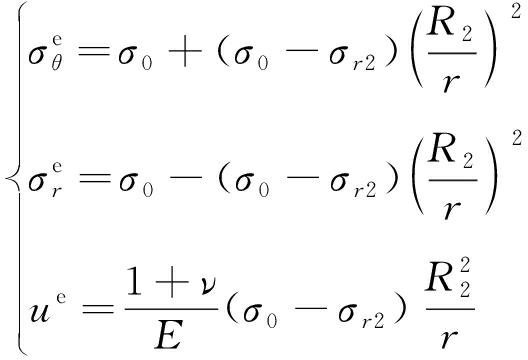
(10)
式中,E为岩体的弹性模量;ν为泊松比。
结合式(8)和(9),那么,弹塑性交界面处岩体所受的径向应力σr2(即此处的围压):
σr2=[σ0(2+b)(1-sin φpeak)-2(1+
b)cpeakcos φpeak]/(2+b+bsin φpeak)
(11)
在应变软化模型中,塑性软化区域内各个参数都随着塑性软化系数的增加而变化,使得塑性软化区内每一处的屈服强度都不相同,因此,无法得到软化区域内的解析解。BROWN[15]提出将塑性区按照相同的切向应变增量划分,利用有限差分的方法求解隧道岩体塑性软化问题;随后,PARK等[4]考虑塑性区弹性应变,改进了BROWN法;同时,LEE和PIETRUSZCZAK[3]提出将塑性区按相等的应力增量划分,围压逐渐递减的差分方法;WANG等[16]提出了将软化区划分成n个残余分段,从弹塑性交界面逐步计算至洞壁。本文采用LEE和PIETRUSZCZAK的划分方法,塑性区被划分为n个同心圆,划分示意图如图3所示。
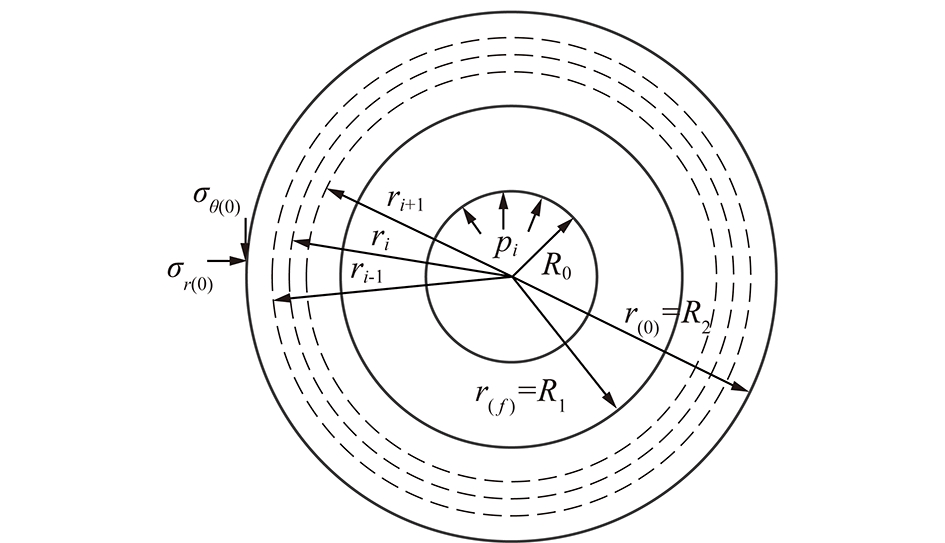
图3 塑性区域划分示意
Fig.3 Dividing schematic diagram in the plastic zone
笔者采用围压逐步释放的方法求解,即假设支护力为pi,当pi≥σr2时围岩在弹性区,采用式(10)计算围岩的应力和位移;当σr1<pi<σr2时围压处于应变软化阶段,不出现塑性残余区;当pi<σr1时围岩出现塑性残余区。由弹塑性交界面处递减逐步向隧道洞壁处逼近,由σr2经过n次等量降至pi,那么每次循环应力降低Δσr:
(12)
值得注意的是,这样划分后从弹塑性交界面至隧道洞壁处,环与环之间按照等量的Δσr从σr2逐步递减至pi,但是环与环之间的厚度并不相等,下面的式(15)和式(25)的计算结果也说明r(i)/r(i-1)并不是常数。
第i环的围压为
σr(i)=σr(i-1)+Δσr
(13)
将式(13)代入式(2)中,第i环的切向应力为
![]()
(14)
式中,
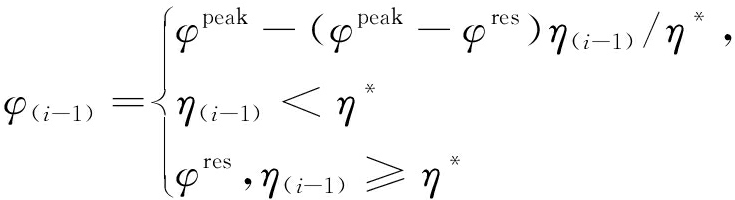
c(i-1)的表达式与φ(i-1)相同,η(0)=0。
利用有限差分法书写式(8)为
(15)
整理式(15),可以得到环与环半径之比d(i):
(16)
根据广义虎克定律,第i环的弹性应变增量为

(17)
式中,![]() 和
和![]() 分别为第i环的径向和切向的弹性应变增量;Δσr(i)=Δσr,Δσθ(i)=σθ(i)-σθ(i-1)。
分别为第i环的径向和切向的弹性应变增量;Δσr(i)=Δσr,Δσθ(i)=σθ(i)-σθ(i-1)。
根据非相关性流动法则可知:
(18)
第i环围岩的应变增量是由弹性部分和塑性部分组成,可以表示为
(19)
根据非流动法则,第i环的应变满足:
εr(i)+Kψεθ(i)=εr(i-1)+Kψεθ(i-1)+Δεr(i)+
![]()
(20)
设定![]() 由式(20)可得
由式(20)可得
εr(i)=B(i-1)-Kψεθ(i)
(21)
εθ(i)=(B(i-1)-εr(i))/Kψ
(22)
围岩的变形协调方程[17]为
(23)
每一环的变形协调方程,式(23)可以改写成
(24)
由式(24)可得
(25)
将式(21)和(22)分别代入式(25),并联立式(15),每一环的应变εθ(i)和εr(i)表达式分别为:
(26)
![]()
(27)
将式(26),(27)和(17)代入式(19)得到塑性应变增量![]() 和
和![]() 根据式(3)进而得到每一环的塑性软化系数η(i)为:
根据式(3)进而得到每一环的塑性软化系数η(i)为:
η(i)=η(i-1)+Δη(i)
(28)
式中,![]()
当η(f)=η*时,此处为软化区与残余区交界面,σr(i)=σr1。
将边界条件(r=R0,σr=pi;r=R1,σr=σr1)代入式(8)中,计算可得
(29)
将n个式(16),相乘可得
(30)
根据上式,可以计算出塑性区半径![]()
由此可以计算每一环半径r(i):
(31)
将式(26),(31)代入式(9),每一环的径向位移ur(i)可得
ur(i)=εθ(i)r(i)=
![]()
(32)
在应变软化模型下,考虑中间应力的隧道围岩特征曲线的计算步骤如下:
(1)计算σr(i)和σθ(i)(式(13)和(14)),其中设n=500,σr(0)=σr2是将围岩的材料峰值(cpeak和φpeak)代入式(11)得到,σθ(0)=2σ0-σr(0)。
(2)计算d(i)=r(i)/r(i-1)(式(16))。
(3)计算每一环的弹性应变![]() 和
和![]() 式(19))。
式(19))。
(4)计算每一环的应变εθ(i)和εr(i)(式(26),(27))。将B(i-1)和d(i)代入式(26)和(27),其中,εr(0)=(σr2-σ0)/(2G),εθ(0)=(σ0-σr2)/(2G)。
(5)计算η(i)(式(28)),其中η(0)=0。
若![]()
若η(i)≥η*,c(i)=cres,φ(i)=φres。
(6)判断η(i)是否与η*相等,当i=f时,η(f)=η*,σr(f)=σr1,R1可以通过式(29)计算。
当i=n时,R2可以通过式(30)计算,隧道硐室的塑性区位移收敛ur(i)通过式(32)计算。
为了验证本文所提应变软化方法的正确性,选取文献[3]中的软化围岩,具体参数如下:R0=3 m,ν=0.25,E=10 GPa,σ0=20 MPa,φpeak=30°,φres=22°,cpeak=1 MPa,cres=0.7 MPa,ψpeak=ψres=3.75°,η*=0.008。在文献[3]中,该围岩用于与Alonso[2]的自相似解法相比较,验证Lee & Pietruszczak法的正确性。为此,在Lee & Pietruszczak法中考虑中间主应力,设定b=0.5,并Lee & Pietruszczak法计算的结果与本文计算的相应的结果对比分析,图4为本文方法计算的围岩特征曲线、塑性区半径和应力分布与Lee & Pietruszczak法的比较图。由图4可知,利用本文的应变软化方法计算所得围岩特征曲线、塑性区半径和塑性区的应力分布,与Lee方法计算所得的结果较吻合,验证了本文方法的正确性。
为研究中间主应力对隧道洞室周围围岩的力学特性的影响,将实例验证中围岩的中间主应力影响系数b分别取0,0.25,0.50,0.75和1.00。需要说明的时,当b=0时,即不考虑中间主应力的影响,退化为M-C理论;当b=1时,中间主应力的影响最大,退化为双剪强度理论。同时,由于不同力学模型对隧道围岩的力学特性影响很大,特此分别计算了弹塑性模型elastic-perfect plastic (EPP),弹脆性模型elastic brittle (EB)和应变软化模型strain softening(SS)下围岩的塑性区半径,塑性区应力分布和围岩特征曲线比较说明,其中将η*设定为0,则力学模型对应于弹塑性模型,同样的,而将η*设定为10 000(足够大),则对应于弹脆性模型。
图5为EPP,EB和SS下考虑中间应力不同影响程度塑性区半径与支护力之间的关系图。
从图5可以看出的规律如下:
(1)随着支护力pi的增加,塑性区半径R2逐渐减小。当支护力与弹塑性交界面的围压相等(σr2)时,即pi=σr2,隧道围岩不出现塑性区;在SS下,当pi=σr1时,围岩只有塑性软化区,没有塑性残余区。
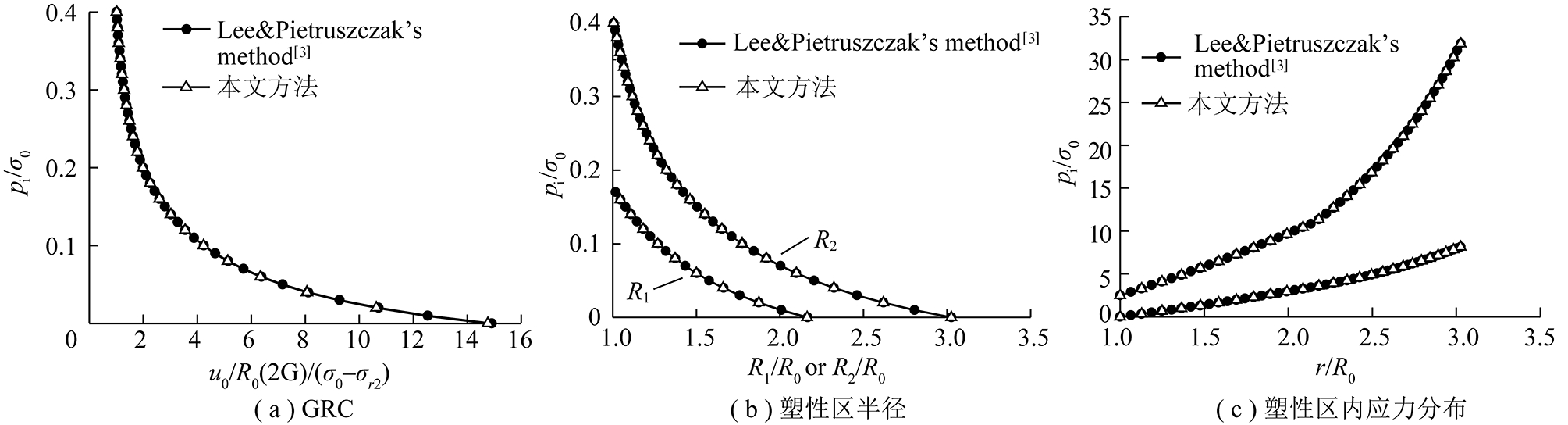
图4 3种方法计算结果的比较
Fig.4 Comparisons between the results calculated by three different methods
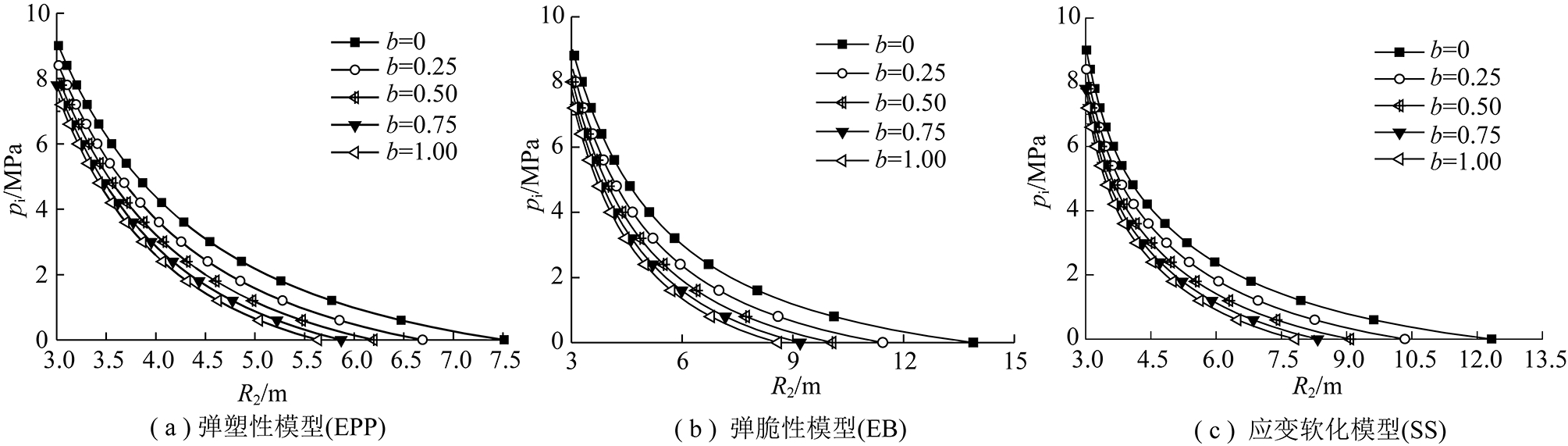
图5 3种力学模型下塑性半径与支护力关系曲线
Fig.5 Distributions of plastic radius under three mechanics models
(2)在相同支护力pi下,EPP的塑性区半径R2最小,SS次之,EB最大,这是由于EPP采用围岩的强度峰值计算,而EB采用围岩的强度残值计算,导致EB的塑性区半径较大。
(3)随着b的增加,塑性区半径R2逐渐减小,这说明中间主应力能有效的抑制塑性区的发展,而且随着隧道洞壁支护力的减小,中间主应力对塑性区半径的抑制作用越显著,特别是当无支护力作用时,此时b=0下的塑性区半径较b=1大了33.3%(EPP)、65.5%(EB)和57.75%(SS),这说明中间主应力对塑性区半径R2的抑制作用EB最大,SS次之,EPP最小。
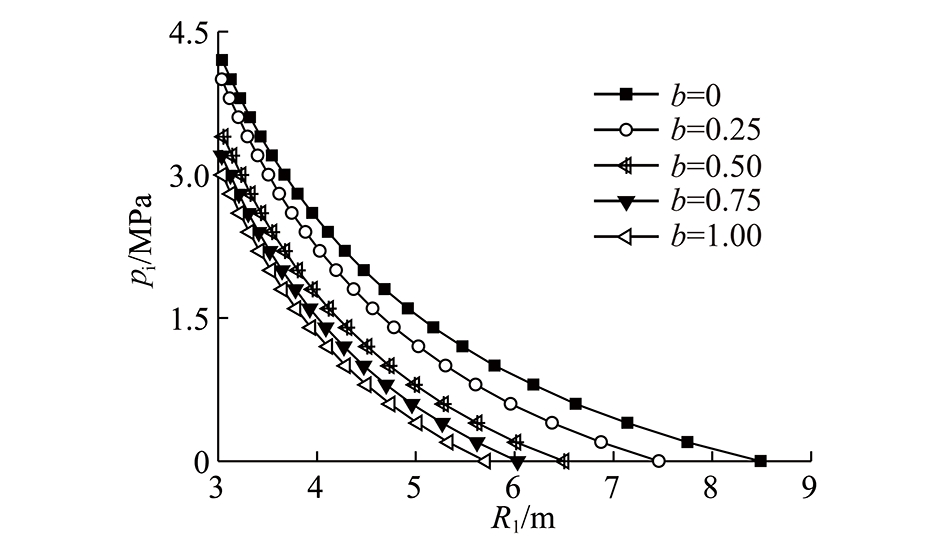
图6 应变软化模型下R1随pi变化
Fig.6 Curves of R1 versus pi under strain-softening model
在SS中,软化区与残余区交界面处的半径R1是塑性区内η=η*处的半径,此处为软化区向残余区转化的临界处。图6为R1随支护力pi和中间主应力影响系数b变化曲线。需要说明的,图6中纵坐标的交点为σr1,即在洞壁处(r=R0)即将出现塑性残余区的支护力。由图6可知,当pi=σr1时,塑性区不出现残余区(R1=R0),只有当pi<σr1时才出现残余区,且随着支护力pi和b的增加,残余区半径逐渐减小。同样说明,增加支护力pi和b都能抑制塑性区的发展。对比图5(c)和图6可以看到,在接近于硐壁处(r=R0)不出现塑性区(pi=σr2)时,中间应力对塑性半径R2的影响较小,但是在接近硐壁处(r=R0)不出现塑性软化区(pi=σr1)时,中间主应力对R1的影响明显。这是由于支护力减弱了中间主应力对围岩承载力潜力的发挥。
图7为EPP,EB和SS下塑性区域内应力σθ,σr分布图,其中虚线代表不同b值下的弹塑性交界面,即塑性区半径的大小。由图7可知:

图7 3种力学模型下塑性区应力分布
Fig.7 Stress distributions in the plastic zone under three mechanics models
(1)随着b值的增加,虚线的位置逐渐左移,说明塑性区半径R2逐渐减小,同时看到虚线之间的间距也逐渐减小,即增加相同b值,塑性区半径R2减小的速率逐渐减小,这说明中间主应力对塑性区半径的抑制速率逐渐减弱。
(2)随着b值的增加,σθ和σr在弹塑性交界面的值变化不大,这就导致围岩应力在塑性区变化速率逐渐增加。由于EPP的塑性区半径R2最小,EB最大,那么在塑性区域内EPP应力变化速率最大,EB最小。
(3)图7(c)为应变软化模型下的塑性区应力分布,可以看出σθ的变化速率沿半径方向表现为软化区变化速率大于残余区,这是由于围岩的强度在软化区内逐渐弱化的结果。
表1为不同b值下交界面的围压σr2值。图8为中间主应力对软化区与残余区交界面处围压σr1的影响。首先,由表1可知,σr2不随支护力的变化而变化,随着b值的增加而减小,这与支护力无关。其次,由图8可知,σr1也不随支护力的变化而变化,但是它随着b值的增加而减小,这是由于b取值直接影响软化区内屈服强度准则(式(15)),从而影响σr1。
表1 不同b值下交界面处的围压σr2和σr1
Table 1 Value of σr2 and σr2 under different mechanics and b


图8 中间主应力对软化区残余区交界处的影响
Fig.8 Effect of the intermediate stress on the confining stress at the boundary of softening-residual zone
综上所述,σr1和σr2均不随支护力的变化而变化,但随b值的增加而减小。
GRC为隧道洞壁处支护力pi与围岩径向位移u0之间的关系曲线,是隧道设计方法——收敛约束法中重要的组成部分,直接与支护结构的设计相关。因此,围岩的GRC对隧道支护结构的设计具有至关重要的作用。
在3种力学模型下(EPP,EB和SS),考虑中间主应力对u0的影响,做出了GRC,如图9所示。从图9可以看出:
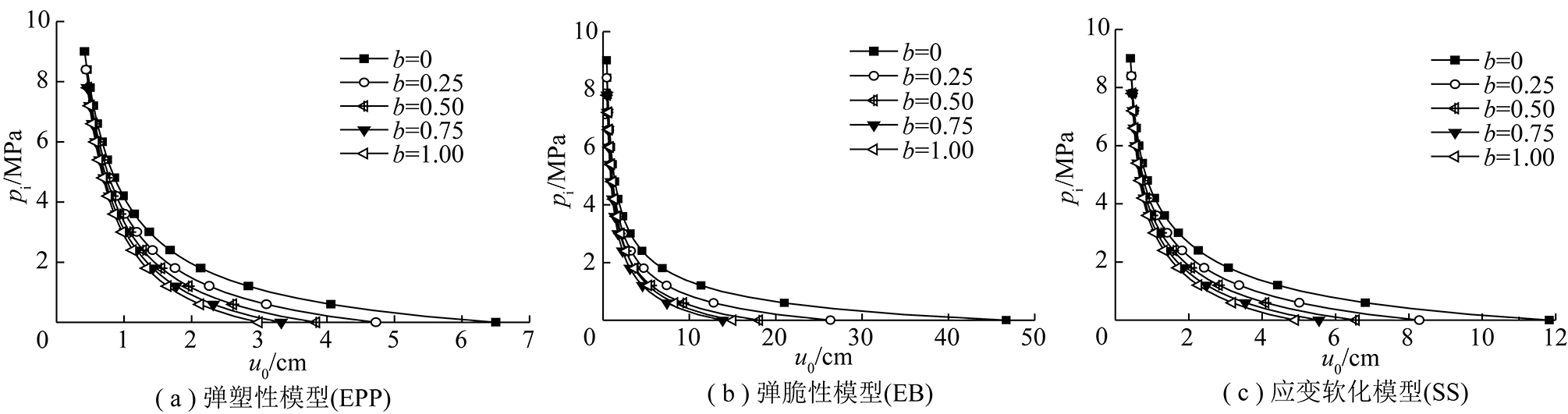
图9 3种力学模型下GRCs
Fig.9 Ground response curves under three mechanics models
(1)u0随pi的减小而增加,相同支护力下,EB计算的u0最大,SS次之,EPP最小,特别是无支护状态下,EB计算的u0最大值为63.75 cm,但是EB计算的u0最大值只有为6.5 cm,这说明若在实际隧道工程的支护结构设计中采用EB时,设计的支护结构刚度较大,较保守,而采用EPP时,对围岩u0的评估不足,设计的支护结构刚度低,易发生支护结构坍塌。因此,在隧道支护结构设计中,应该避免采用弹塑性模型,并根据围岩的力学特性合理的选择合适的力学模型。
(2)u0随b的增加而显著减小,这说明考虑中间主应力作用下的u0较不考虑中间主应力作用下的u0小,因此,在实际中考虑中间主应力可以增加围岩的承载能力。
(3)中间主应力对u0的影响随pi的增加而减小,在支护力较高时,中间主应力对位移的收敛作用不明显。但是在无支护状态下,考虑中间主应力的作用下的u0显著小于不考虑中间主应力的作用,特别是对EB。由图9(b)可以看到,EB在b=0状态下的u0为63.75 cm,而b=1状态下的u0为15.02 cm,足足较b=0减小了3.2倍,这表明在弹脆性模型下,中间主应力对隧道硐壁处的位移收敛作用显著。
(1)弹塑性模型计算的塑性区半径,应力和硐壁处位移均较小,没有考虑围岩强度在塑性区的弱化,在实际隧道设计中应慎重选择。
(2)根据中间主应力影响系数b和支护力pi对塑性发展的研究结果可知,中间主应力能有效抑制塑性区半径和隧道硐壁处位移的发展,特别是对无支护状态的弹脆性模型下隧道围岩的塑性发展的抑制效果最显著,能充分发挥围岩潜在的承载力。
(3)围岩的弹塑性交界面处围压,及软化模型中软化区与残余区交界面的围压均不受支护力的影响,但均随着b的增加而减小。
(4)随着支护力pi的增加,中间主应力对塑性区半径和硐壁处位移的抑制作用逐渐减小,而且这种抑制作用随着b的增大而减小。因此,当支护力较大时可以不考虑中间主应力对塑性发展的抑制作用。
(5)本文的研究结果均是在一系列的基本假定的基础上建立的,没有考虑围岩材料的不均匀性,中间主应力对隧道围岩承载力的影响程度需进一步的试验研究。
参考文献
[1] CARRANZA-TORRES C,FAIRHURST C.Application of the Convergence-Confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion[J].Tunnelling & Underground Space Technology,2000,15(2):187-213.
[2] ALONSO E,ALEJANO L R,VARAS F,et al.Ground response curves for rock masses exhibiting strain-softening behaviour[J].International Journal for Numerical & Analytical Methods in Geomechanics,2003,27(13):1153-1185.
[3] LEE Y K,PIETRUSZCZAK S.A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass[J].Tunnelling & Underground Space Technology,2008,23(5):588-599.
[4] PARK K H,TONTAVANICH B,LEE J G.A simple procedure for ground response curve of circular tunnel in elastic-strain softening rock masses[J].Tunnelling & Underground Space Technology,2008,23(2):151-159.
[5] ALEJANO L R,RODRIGUEZ-DONO A,ALONSO E,et al.Ground reaction curves for tunnels excavated in different quality rock masses showing several types of post-failure behaviour[J].Tunnelling & Underground Space Technology,2009,24(6):689-705.
[6] González-Cao J,VARAS F,BASTANTE F G,et al.Ground reaction curves for circular excavations in non-homogeneous,axisymmetric strain-softening rock masses[J].Journal of Rock Mechanics and Geotechnical Engineering,2013,5(6):431-442.
[7] XU S Q,YU M H.The effect of the intermediate principal stress on the ground response of circular openings in rock mass[J].Rock Mechanics and Rock Engineering,2006,39(2):169-181.
[8] YU M H,HE L N.TS2e4 - a new model and theory on yield and failure of materials under the complex stress state[J].Mechanical Behaviour of Materials VI,1992:841-846.
[9] 俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报,1994,16(2):1-10.
YU Maohong.Unified strength theory for geomaterials and its applications[J].Chinese Journal of Geotechnical Engineering,1994,16(2):1-10.
[10] 张强,王红英,王水林,等.基于统一强度理论的破裂围岩劣化弹塑性分析[J].煤炭学报,2010,35(3):381-386.
ZHANG Qiang,WANG Hongying,WANG Shuilin,et al.Deterioration elasto-plastic analysis of cracked surrounding rocks based on unified strength theory[J].Journal of China Coal Society,2010,35(3):381-386.
[11] 张常光,赵均海,范文.围岩塑性区变形特性对隧道收敛约束的影响[J].中国公路学报,2016,29(3):106-115.
ZHANG Changguang,ZHAO Junhai,FAN Wen.Influence of deformation characteristics of surronding rock in plastic zone on tunnel convergence-confinement[J].China Journal of Highway and Transport,2016,29(3):106-115.
[12] CAI M.Influence of intermediate principal stress on rock fracturing and strength near excavation boundaries—Insight from numerical modeling[J].International Journal of Rock Mechanics & Mining Sciences,2008,45(5):763-772.
[13] HOEK E,BROWN E T.Practical estimates of rock mass strength[J].International Journal of Rock Mechanics & Mining Sciences,1997,34(8):1165-1186.
[14] VERMEER P A,DE BORST R.Non associated plasticity for soils,concrete and rock[J].Heron,1984,29(3):3-64.
[15] BROWN E T,BRAY J W,LADANYI B,Et al.Ground response curves for rock tunnels[J].Journal of Geotechnical Engineering,1983,109(1):15-39.
[16] WANG S,YIN X,TANG H,et al.A new approach for analyzing circular tunnel in strain-softening rock masses[J].International Journal of Rock Mechanics & Mining Sciences,2010,47(1):170-178.
[17] FLORENCE A L,SCHWER L E.Axisymmetric compression of a Mohr-Coulomb medium around a circular hole[J].International Journal for Numerical & Analytical Methods in Geomechanics,2010,2(4):367-379.