
杨 阳1,2,米玉泉1,李 明1,秦大同1,2
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.重庆大学 汽车工程学院,重庆 400044)
摘 要:针对传统采煤机截割传动系统存在传动链过长、可靠性差、突变工况调速性能差的特点,在提出的多源驱动的采煤机短程截割传动系统的基础上,采用集中参数法建立了系统平移-扭转-轴向耦合动力学模型,进行了系统固有特性分析。结果表明,耦合轮系和行星轮系耦合时重根频率不变,单根频率发生变化;单根振动模式变得更为复杂,重根振动模式与原来保持一致;模态能分布与构件形变振动状态一致;耦合轮系支撑刚度和构件质量对系统高阶固有频率影响较大,行星轮系支撑刚度对系统低阶固有频率影响较大;而啮合刚度均对高阶固有频率影响较大。对系统激励频率和固有频率对比分析,发现系统低速运行时可能发生共振。研究结果可为避免系统出现共振现象和实现动态特性优化提供理论依据。
关键词:采煤机;短程截割传动系统;耦合轮系;人字齿行星轮系;固有特性分析
中图分类号:TD421
文献标志码:A
文章编号:0253-9993(2018)11-3232-08
YANG Yang1,2,MI Yuquan1,LI Ming1,QIN Datong1,2
(1.State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400044,China; 2.College of Automotive Engineering,Chongqing University,Chongqing 400044,China)
Abstract:In terms of the long transmission chain,poor reliability and poor speed adjusting performance in the sudden change of working conditions in the traditional shearer cutting transmission system,the coupling dynamic model of translational-torsional-axial is established by using the centralized parameter method based on a multi-source driving cutting system.Compared with the original system,the results on the natural characteristics of the system show that the frequency of the single root changes slightly and the multiple root is the same when the coupling wheel train and the planetary gear train are coupled.However,the vibration mode of the multiple root frequency is the same as that in the original system.The distribution of modal energy is in accordance with the state of deformation and vibration.The stiffness of the coupling train has a great influence on the high-order natural frequency of the system,and so does the stiffness of the planetary gear train on the natural frequency of the system.The mesh stiffness and the mass have great influence on the high-order natural frequency and little influence on the low-order natural frequency.Also,it is found that the system may resonate at low speed.The results of this study can provide a theoretical basis for avoiding system resonance and dynamic characteristic optimization.
Key words:coal shearer;short cutting system;coupling wheel train;herringbone planetary gear train;natural characteristic

移动阅读
杨阳,米玉泉,李明,等.多源驱动的采煤机短程截割传动系统固有特性分析[J].煤炭学报,2018,43(11):3232-3239.doi:10.13225/j.cnki.jccs.2017.1850
YANG Yang,MI Yuquan,LI Ming,et al.Analysis of natural characteristics of multi-source driving short cutting transmission system of coal shearer[J].Journal of China Coal Society,2018,43(11):3232-3239.doi:10.13225/j.cnki.jccs.2017.1850
收稿日期:2017-12-29
修回日期:2018-10-16
责任编辑:毕永华
基金项目:国家重点基础研究发展计划(973)资助项目(2014CB046304)
作者简介:杨 阳(1958—),男,四川成都人,教授,博士。E-mail:yangyang@cqu.edu.cn
深层采煤的复杂条件对装备工作可靠性和工况适应能力要求越来越高,成为制约采煤生产效率的主要因素[1-2]。针对传统采煤机截割部传动链过长、可靠性能低、不可调速和自适应能力差的特点,孙冬野等[3]提出了一种基于多源驱动的新型采煤机截割传动系统,该系统由耦合轮系和行星轮系组成,只有两级齿轮传动,缩短了传动链,提高了系统工作可靠性、调速性能以及工况自适应能力,提高了煤炭生产效率和系统可控性能。
对于单独的耦合轮系或行星轮系动力学,国内外学者做了大量研究。在耦合轮系方面,研究重点集中在动态特性和均载特性。WEI等分析了其动态特性和均载特性,为多源耦合驱动提供相关依据[4]。YANG等分析了变负载工况下的均载性能,得出输入转速不同步比输入扭矩不同步对均载的影响更大[5]。在行星轮系方面,已有较全面的研究[6],KAHRAMAN A,宋轶民等对直齿行星轮系固有特性进行了分析,并推导出支承刚度大于啮合刚度10倍时可以用纯扭转模型研究系统固有特性[7-8];杨通强,张俊等考虑了构件6个自由度对斜齿行星轮系固有特性进行了分析[9-10];PARKER R G,秦大同等分析了输入转速对其动态特性的影响[11-12];卜忠红,刘更等考虑轴承支承刚度不对称的因素对滑动轴承支承的人字齿轮行星传动固有特性和模态进行了分析,并归纳出了5种振动模式[13-14]。
以上研究涉及到单级齿轮动力学问题较多,针对多级齿轮耦合的动力学问题研究较少,而多级耦合时模态表现更为复杂。采用多源驱动的耦合-行星轮系系统在调速时激励频率会发生变化,可能发生共振现象,同时,系统参数(刚度、质量等)设计不当就有可能发生系统共振现象。因此,对系统的固有特性研究具有重要意义。
如图1所示,该系统基于MG300/700-WD型采煤机设计。原采煤机截割系统是由摇臂底部经多级齿轮系统向摇臂头传递截割能量,这样就导致了系统传动链过长,可靠性低,由于没有安装变频器,系统不可调速等缺点。本系统是由三台电机、耦合轮系、人字齿行星轮系组成,三台电机分别带动小齿轮驱动大齿轮转动,完成一级减速,大齿轮输出连接太阳轮,带动行星轮系转动,行星架输出,完成二级减速,行星架再连接截割滚筒,实现截割采煤的工作过程。该系统具有体积小,可安装在滚筒内部,可避免摇臂箱体变形对传动系统的影响。系统电机调速范围900~1 480 r/min,滚筒调速范围18.6~30.5 r/min。
如图2所示,以传动系统整体为研究对象,运用集中参数法建立了耦合轮系平移-扭转动力学模型、人字齿行星轮系平移-扭转-轴向动力学模型。系统由于低速运行,忽略了由于行星架转动带来的陀螺效应和向心力的影响。
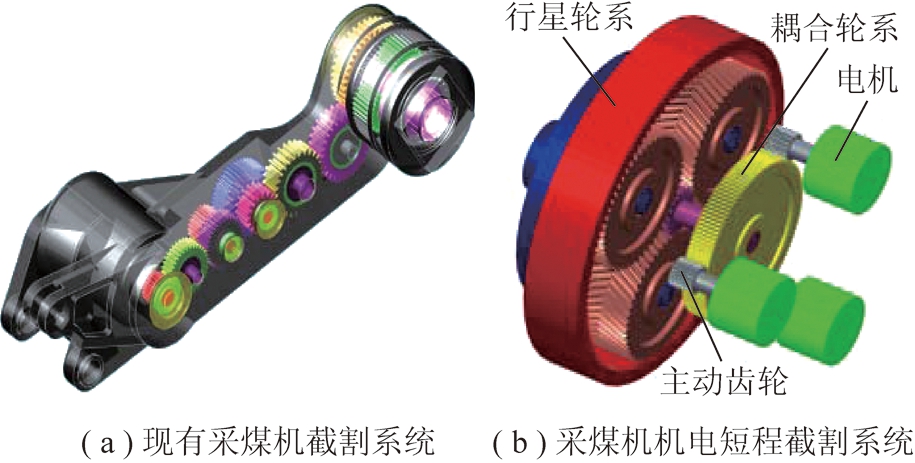
图1 系统结构
Fig.1 Schematic diagram of electromechanical short cutting transmission system
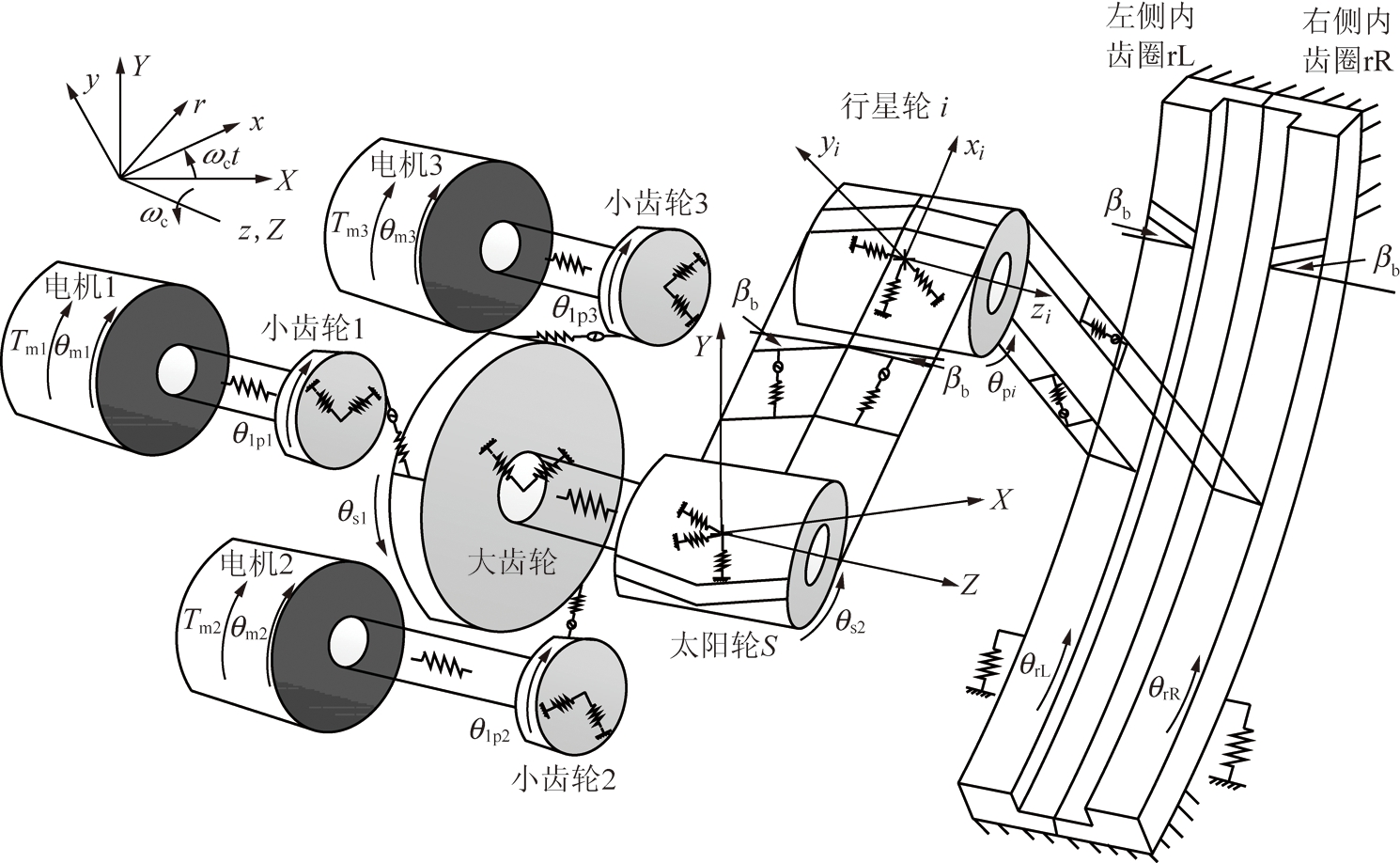
图2 动力学模型
Fig.2 Dynamic model of electromechanical short cutting transmission system
耦合轮系动力学模型如下[5]:电机轴i的运动微分方程为
(1)
式中,Imi为第i个电机转动惯量;km1pi为第i个电机轴扭转刚度;θmi为第i个电机转动角度;θ1pi为第i个小齿轮转动角度;Tmi为第i个电机输出转矩。
第i个小齿轮与大齿轮啮合副在啮合线上的弹性形变:
δ1pis=-x1picos α+y1pisin α+r1piθ1pi+
xs1cos(φ1i+α)-ys1sin(φ1i+α)-
rs1θs1-e1pis
(2)
式中,x1pi为第i个小齿轮x向振动位移;y1pi为第i个小齿轮y向振动位移;r1pi为第i个小齿轮基圆半径;θ1pi为第i个小齿轮扭转角度;xs1为大齿轮x向振动位移;ys1为大齿轮y向振动位移;rs1为大齿轮基圆半径;θs1为大齿轮扭转角度;α为小齿轮与大齿轮啮合角;第i个小齿轮位置角φ1i=2π(i-1)/N,i为第i个小齿轮,N为小齿轮总个数;e1pis为第i个小齿轮与大齿轮啮合误差。
小齿轮i的运动微分方程为
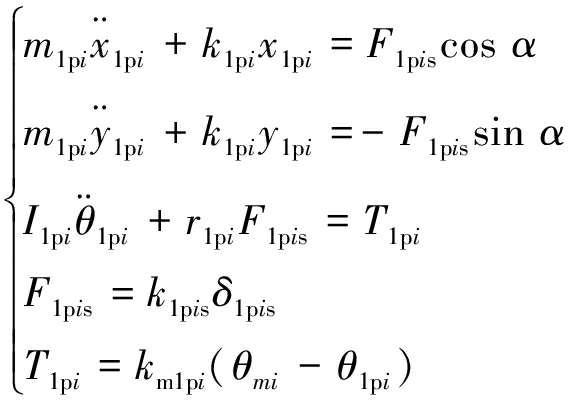
(3)
式中,m1pi为第i个小齿轮质量;I1pi为第i个小齿轮转动惯量;k1pi为第i个小齿轮支承刚度;F1pis为第i个小齿轮与大齿轮啮合力;k1pis为第i个小齿轮与大齿轮啮合刚度;T1pi为第i个小齿轮输入扭矩。
大齿轮的运动微分方程为
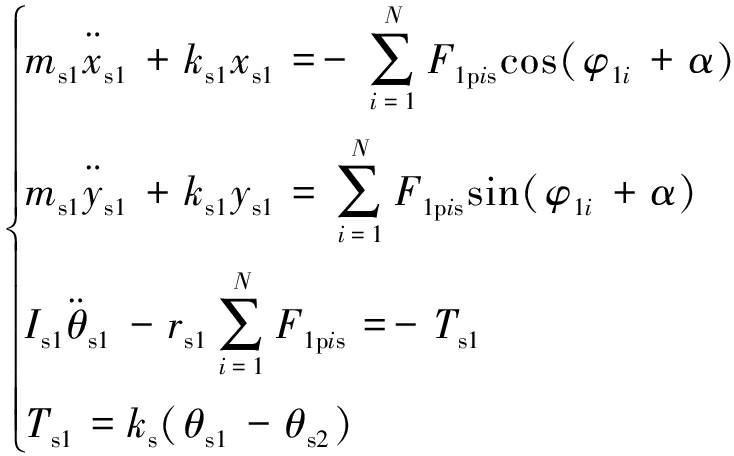
(4)
式中,Is1为大齿轮转动惯量;ks1为大齿轮支承刚度;Ts1为大齿轮输出扭矩;ks为大齿轮与太阳轮连接轴扭转刚度;θs2为太阳轮扭转角度。
人字齿行星轮系动力学模型如下[15]:太阳轮与第i个行星轮右/左侧在啮合线上的弹性形变:
δspiR/L=(-xs2sin φsi+ys2cos φsi+rs2θs2
-ξisin αsi-ηicos αsi+rpiθpi)cos βb+
(∓zs2+zpi)sin βb-espiR/L
(5)
式中,xs2为太阳轮x向振动位移;ys2为太阳轮y向振动位移;zs2为太阳轮z向振动位移;rs2为太阳轮基圆半径;ξi为第i个行星轮x向振动位移;ηi为第i个行星轮y向振动位移;zi为第i个行星轮z向振动位移;θpi为第i个行星轮扭转角度;rpi为第i个行星轮基圆半径;espiR/L为太阳轮与第i个行星轮啮合误差;βb为行星轮系螺旋角;αsi为太阳轮与第i个行星轮端面啮合角。
右/左侧内齿圈与第i个行星轮在啮合线上的弹性形变:
δpirR/L=(-xrR/Lsin φri+yrR/Lcos φri+rrR/LθrR/L+
ξisin αri-ηicos αri-rpiθpi)cos βb+
(∓zrR/L+zpi)sin βb-erpiR/L
(6)
式中,xrR/L为右/左侧内齿圈x向振动位移;yrR/L为右/左侧内齿圈y向振动位移;zrR/L为右/左侧内齿圈z向振动位移;θrR/L为右/左侧内齿圈扭转角度;rrR/L为右/左侧内齿圈基圆半径;erpiR/L为右/左侧内齿圈与第i个行星轮啮合误差;αri为内齿圈与第i个行星轮端面啮合角。
行星架与第i个行星轮沿行星轮径向和切向的弹性形变:
δcpix=xccos φi+ycsin φi-ξi
(7)
δcpiy=-xcsin φi+yccos φi-ηi+rcθc
(8)
式中,xc为行星架x向振动位移;yc为行星架y向振动位移;zc为行星架z向振动位移;θc为行星架扭转角度;rc为行星架基圆半径;第i个行星轮位置角φi=φ2i,φ2i=2π(i-1)/N,i为第i个行星轮,N为行星轮总个数;x,y,z,θ分别表示各构件在OXYZ坐标下各向的振动位移;ξ,η分别表示行星轮在oξηz坐标下的x,y向的振动位移。
行星架运动微分方程:
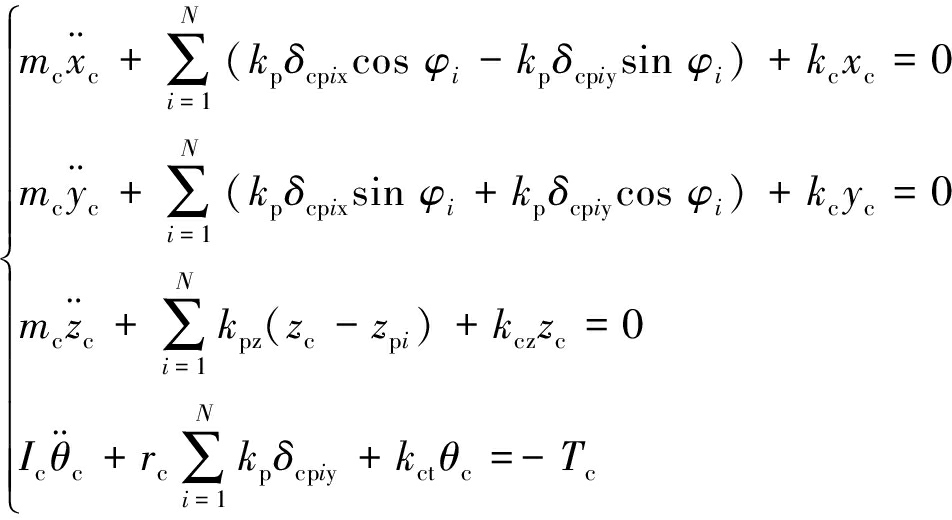
(9)
右侧内齿圈运动微分方程:
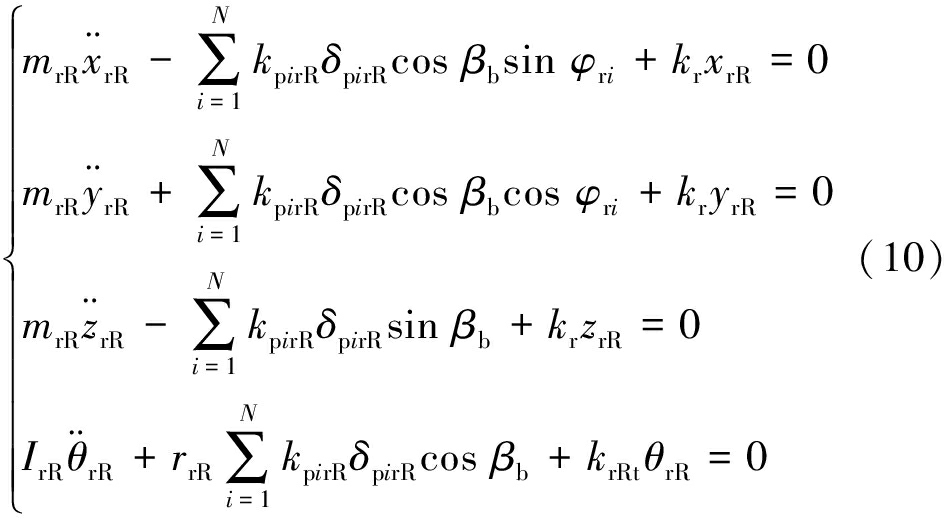
左侧内齿圈运动微分方程:
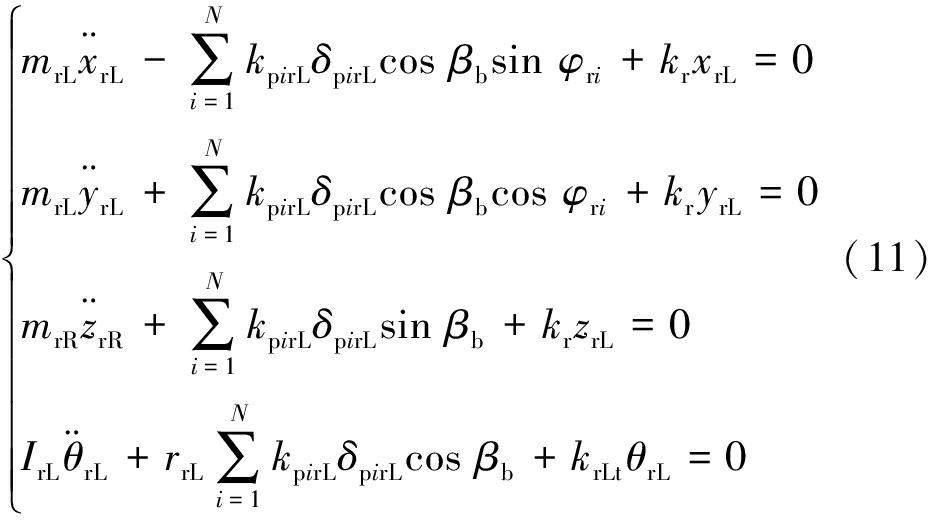
太阳轮运动微分方程:
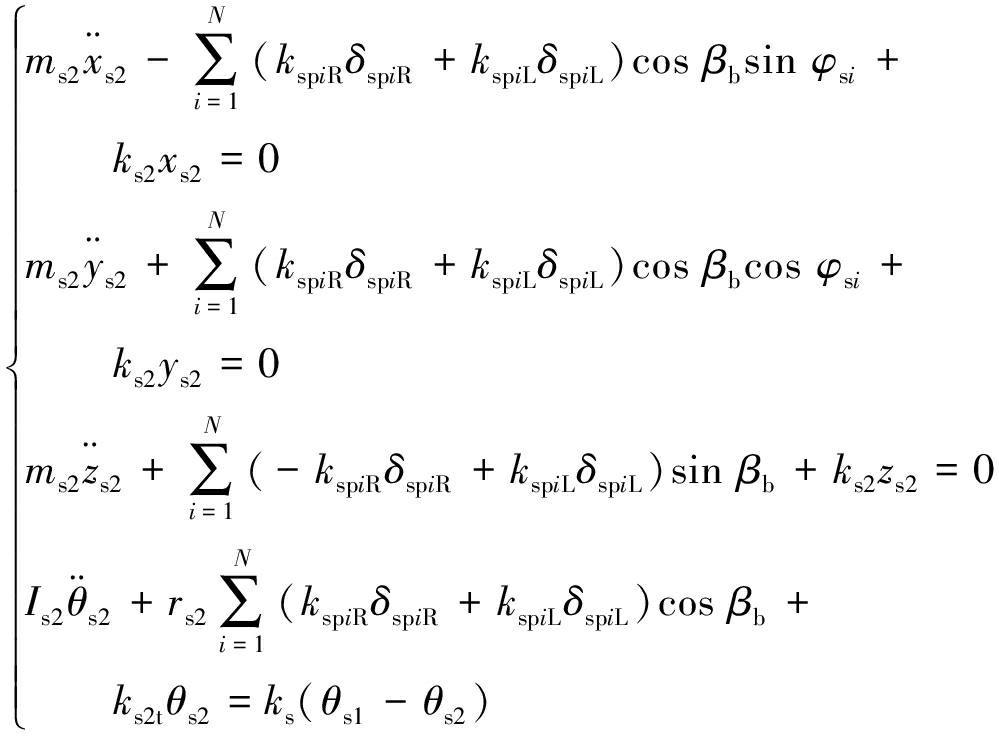
(12)
第i个行星轮运动微分方程:

(13)
式中,kspiR为太阳轮与第i个行星轮右侧啮合刚度;kspiL为太阳轮与第i个行星轮左侧啮合刚度;kpirR为右侧内齿圈与第i个行星轮啮合刚度;kpirL为左侧内齿圈与第i个行星轮啮合刚度;ks2,kr,kp, kc,kpz,kcz分别为各构件的支撑刚度;kct, krRt, krLt分别为各构件的行星架、右/左内齿圈的扭转刚度,其中kct=0,krRt=krLt不为0;φsi=φ2i-αsi,φri=φ2i+αri,αsi=αri=αt,αt为行星轮系端面压力角。
将各方程化为自由振动方程如下:
(14)
式中,M为系统广义质量矩阵;Kb为系统支承刚度矩阵;![]() 为系统平均啮合刚度矩阵;q为系统广义坐标列矢量,其中,
为系统平均啮合刚度矩阵;q为系统广义坐标列矢量,其中,
q=[θm1,x1p1,y1p1,θ1p1,θm2,x1p2,y1p2,θ1p2,θm3,
x1p3,y1p3,θ1p3,xs1,ys1,θs1,xs2,ys2,zs2,θs2,
xrR,yrR,zrR,θrR,xrL,yrL,zrL,θrL,xc,yc,zc,
θc,xp1,yp1,zp1,θp1,…,xpN,ypN,zpN,θpN,]T
(15)
整个系统的振动矢量包括了3个电机轴的扭转,电机与小齿轮通过扭转刚度和扭转阻尼相连接。
系统特征值求解方程为
(16)
式中,ωj为系统第j阶固有频率;ψj为系统第j阶模态振型矢量,ψj=[φ1p1,φ1p2,φ1p3,φs1,φs2,φrR,φrL,φc,φp1,φp2,…,φpN]T。
系统仿真参数见表1(表1中,α表示耦合轮系压力角,行星轮系法面压力角;K1ps为小齿轮与大齿轮平均啮合刚度;Ksp为太阳轮与行星轮平均啮合刚度;Krp为行星轮与内齿圈平均啮合刚度)。
通过特征方程求解得到系统的固有频率见表2。
表1 系统参数
Table 1 Parameters of the system
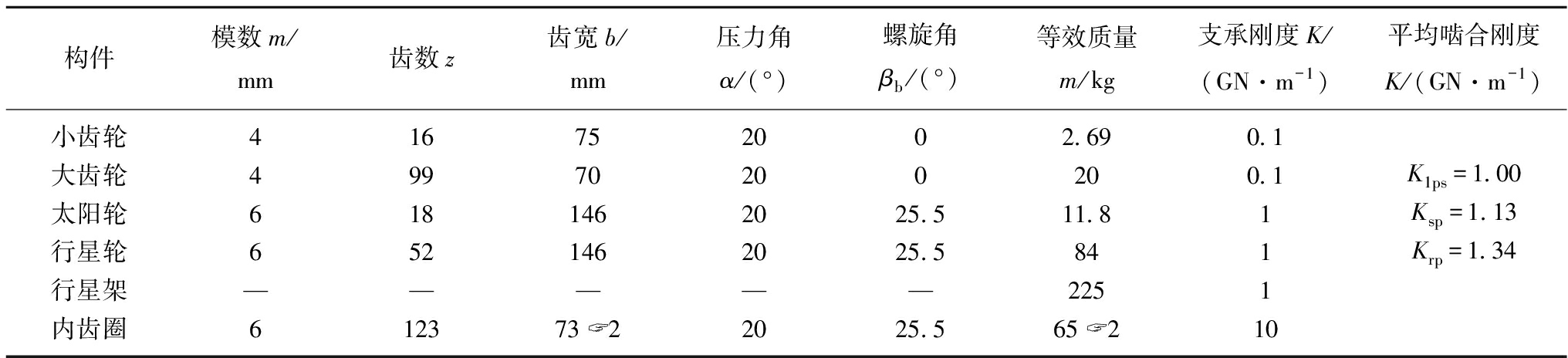
表2 系统固有频率
Table 2 Natural frequency of system
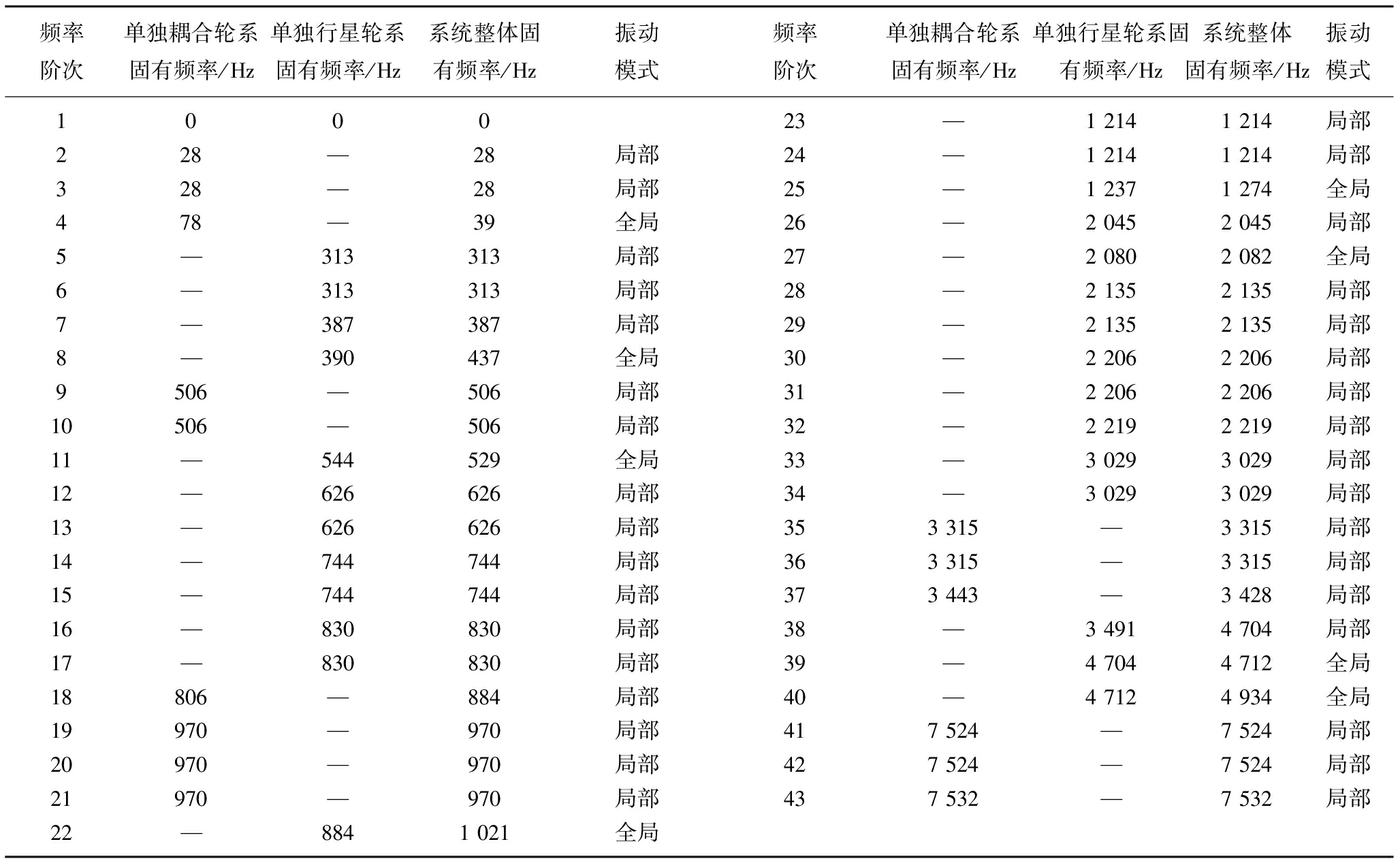
从表2可以看出,耦合轮系和行星轮系单独进行固有频率分析时,其频率大小分布均比较清晰,耦合轮系和行星轮系均存在两重根频率,而当两级连接时,系统重根频率与原来保持一致,单根频率发生改变,第一个全局振动频率减小。
对系统矢量的归纳分类可以得到系统的振动模式,振动模式可以清楚明了的反映各构件的振动状态,为系统动态特性的表现提供依据。系统振动模式大致分为两大类:全局振动模式和局部振动模式(表2),局部振动模式与原来保持一致,全局振动变得更为复杂。下面将选择其中几种进行分析。
3.2.1 全局振动——纯扭转振动模式
如图3所示,该振动模式对应3个单重固有频率;所有构件除行星轮外均只有扭转振动;行星轮存在y向大小相等方向相同的平移振动。
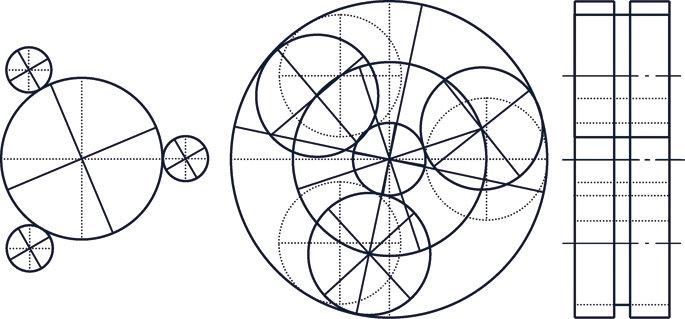
图3 纯扭转振动模式
Fig.3 Pure torsional vibration mode
3.2.2 局部振动——小齿轮横向振动模式
如图4所示,该振动模式对应1个三重固有频率;f=970 Hz;只存在小齿轮横向振动;其余构件均不振动。
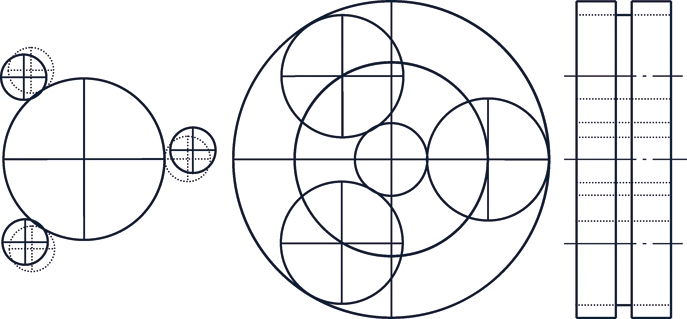
图4 小齿轮横向振动模式
Fig.4 Pinion lateral vibration mode
3.2.3 局部振动——内齿圈横向-行星轮轴向振动模式
如图5所示,该振动模式对应2个二重固有频率;左右内齿圈只存在横向振动,且大小相等,方向相反;行星只存在轴向振动,且振幅之和等于0;其余构件均不振动。
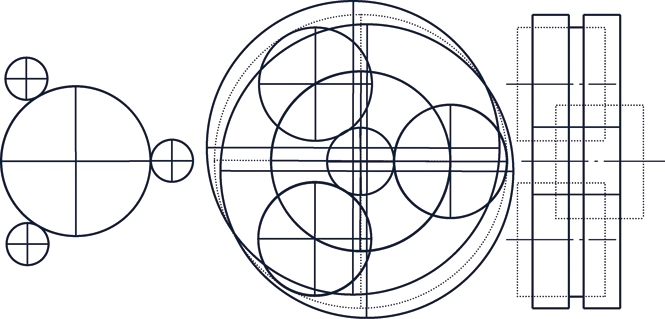
图5 内齿圈横向-行星轮轴向振动模式
Fig.5 Translational ring and axial planet mode
系统模态能是系统各构件振动状态的具体反映,模态能分为模态应变能和模态动能,模态应变能表示构件形变的大小,模态动能表示构件振动剧烈的程度。系统模态应变能和模态动能表示为
式中,Uj为模态应变能;Tj为模态动能;M为系统质量矩阵;K为系统刚度矩阵;ψj为系统第j阶模态振型矢量。
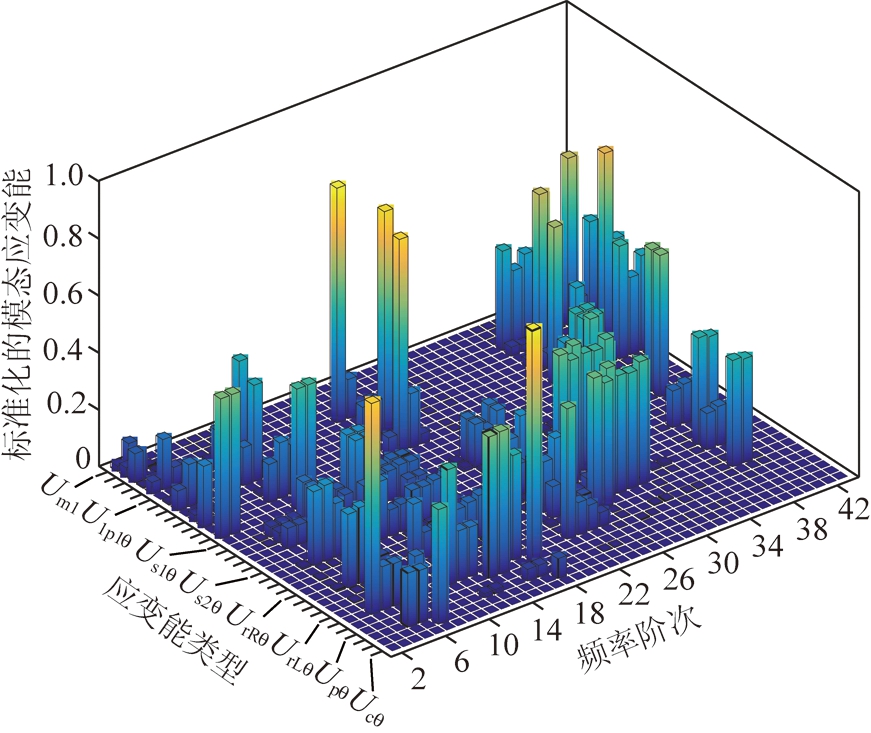
图6 模态应变能(0模态除外)
Fig.6 Strain modal energy (except 0 mode)
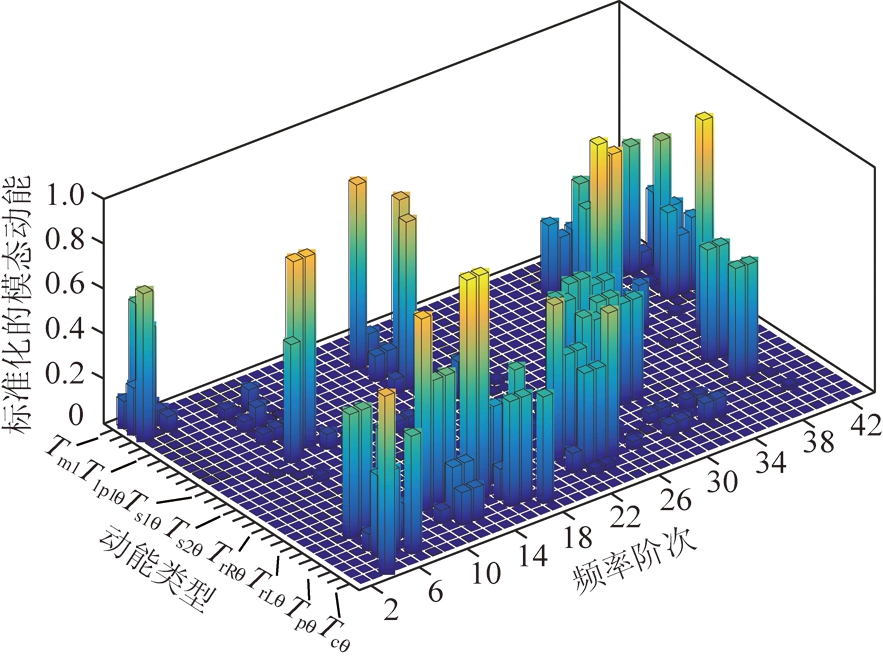
图7 模态动能(0模态除外)
Fig.7 Kinetic modal energy (except 0 mode)
图6给出了系统各构件模态应变能分布,不难看出,模态应变能越大,系统构件形变量越大。图7给出了系统各构件模态动能分布,不难发现,模态动能越大,构件振动越剧烈。人字齿行星传动轴向也存在较大的模态能,设计时不可忽略其轴向的影响。与模态能有关的参数主要是刚度和质量,设计时应充分考虑模态能的大小来调节系统参数变化,以达到模态分布最优化。
系统参数敏感性分析可有效预测系统动态特性,为系统参数设计时避开敏感区域提供理论依据,本节将从系统支承刚度、齿轮啮合刚度、构件质量的变化对系统固有频率的影响进行分析。
如图8(a)所示,太阳轮与行星轮啮合刚度ksp对第32~43阶固有频率均有不同程度的影响;而对系统第1~31阶固有频率影响很小,几乎没有影响。如图8(b)所示,内齿圈与行星轮啮合刚度krp对第22~40阶固有频率均有不同程度的影响;而对系统第1~21阶、41~43阶固有频率影响很小,几乎没有影响。如图8(c)所示,耦合轮啮合刚度对系统k1ps对第35~43阶固有频率均有不同程度的影响,尤其是对第41~43阶固有频率影响较大;而对系统第1~34阶固有频率影响很小,几乎没有影响。如图8(d)所示,耦合轮系支承刚度k1b对第11~43阶固有频率均有不同程度的影响,尤其是对第38~43阶固有频率影响较大;而对系统第1至10阶固有频率影响很小,几乎没有影响。如图8(e)所示,行星轮系支承刚度k2b对第5~43阶固有频率均有不同程度的影响,尤其是对第23阶以上的固有频率影响较大;而对系统第1~4阶固有频率影响很小,几乎没有影响。如图8(f)所示,行星轮支承刚度kp对第5~25、27~40阶固有频率均有不同程度的影响,尤其是对第27~40阶固有频率影响较大;而对系统第1~4阶、26阶、41~43阶固有频率影响很小,几乎没有影响。如图8(g)所示,m表示原质量时各阶固有频率;其余分别表示各构件的质量增大一倍时系统各阶固有频率的变化,可以看出,系统固有频率随构件质量增大而减小,尤其是高阶固有频率减小明显。
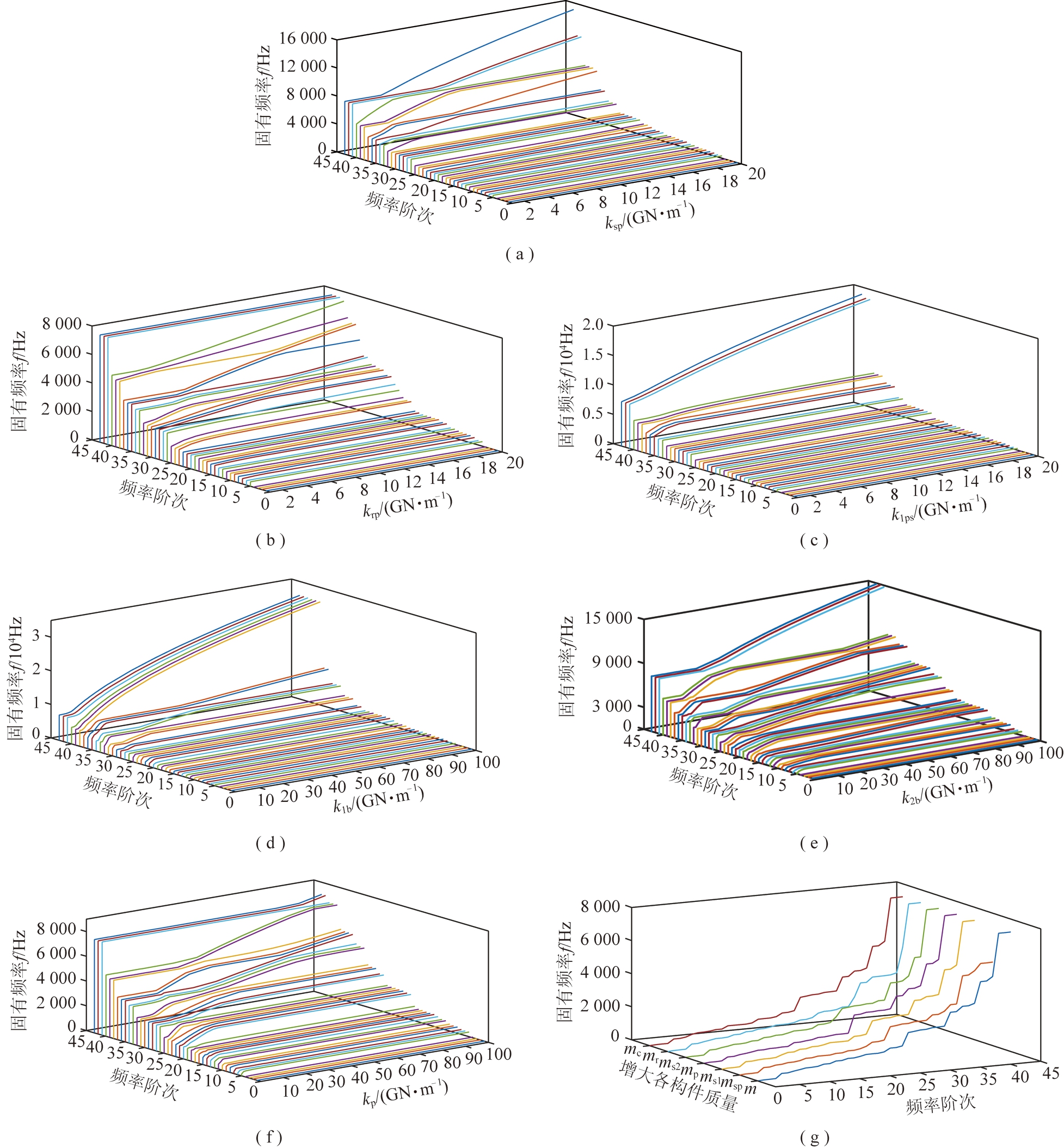
图8 参数变化对系统固有频率的影响
Fig.8 Effect of parameter changes on natural frequency of system
综上所述,耦合轮系支承刚度和系统构件质量主要影响高阶固有频率,系统啮合刚度主要影响高阶固有频率,行星轮系支承刚度主要影响低阶固有频率。设计时应注意行星轮系支撑刚度参数的选择。
系统激励频率分析可发现系统固有频率与激励频率的交点,得出系统可能发生的共振点,为系统工作时有效避开共振点,保障系统安全可靠高效运行。系统外部激励频率为三台电机和负载滚筒,内部激励频率为耦合轮系啮合频率和行星轮系啮合频率,其在电机额定转速范围内的转频和啮频的变化与固有频率的对比如图9所示,电机调速范围为900~1 480 r/min,滚筒调速范围为18.6~30.5 r/min,在此范围内,各啮频与转频均不会与该级固有频率相交,系统可安全调速。但与第一个全局振动固有频率相交,系统可能在此处(A点)发生共振,应避免电机低速运行。
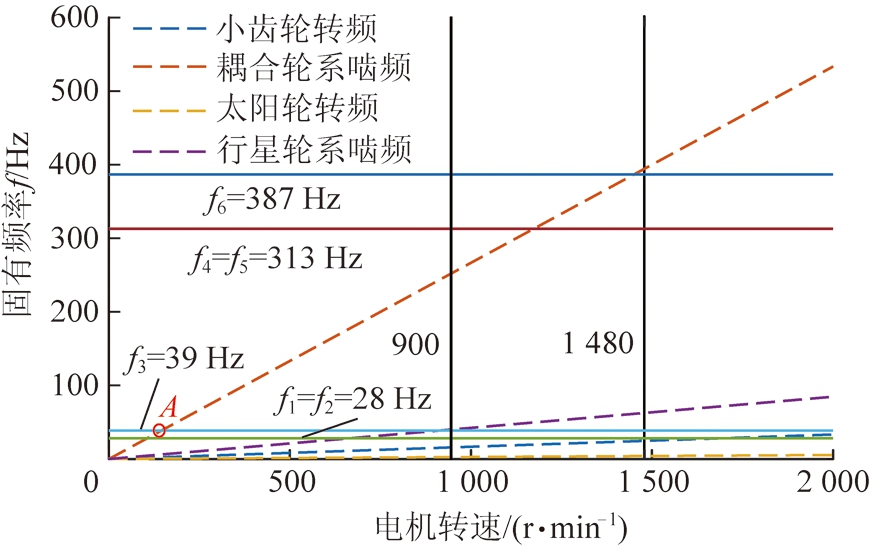
图9 外激励频率与系统固有频率对比
Fig.9 External excitation frequency compared with natural frequency of the system
(1)多级齿轮系统连接时,其固有频率重根不变,单根发生变化。激励频率可与第一个全局振动固有频率相交,可能发生共振,应避免电机低速运行。但在调速范围内不会有共振的危险。
(2)通过归纳系统的振型矢量,分析其各构件的振动模式,可得出清晰的全局和局部振动模式图,为分析系统各构件的振动状态奠定基础。模态能可清晰反映各构件的振动状态,模态应变能越大,构件的弹性形变越大,模态动能越大,构件的振动越剧烈。人字齿行星传动轴向有较大的模态能,设计时不可忽略其轴向对系统的影响。
(3)系统的支承刚度、啮合刚度、构件质量变化均能使系统固有频率发生变化;耦合轮系支承刚度和系统构件质量主要影响高阶固有频率,系统啮合刚度主要影响高阶固有频率,行星轮系支承刚度主要影响低阶固有频率。系统设计时应注意行星轮系支撑刚度参数的选择。
(4)系统在某些参数区域时会发生模态跃迁,模态跃迁会增加系统动态特性的复杂性,系统设计时应该尽量避开参数敏感区域。
参考文献:
[1] 钱鸣高.煤炭的科学开采[J].煤炭学报,2010,35(4):529-534.
QIAN Minggao.On sustainable coal mining in China[J].Journal of China Coal Society,2010,35(4):529-534.
[2] 赵丽娟,刘旭南,马联伟.基于经济截割的采煤机运动学参数优化研究[J].煤炭学报,2013,38(8):1490-1495.
ZHAO Lijuan,LIU Xunan,MA Lianwei.Optimization research on shearer’s kinematic parameters based on economical cutting[J].Journal of China Coal Society,2013,38(8):1490-1495.
[3] 孙冬野,李明,舒锐志,等.采煤机截割部动力传动转置[P].中国专利:ZL201410728258.3,2016-08-17.
[4] WEI J,SUN Q,SUN W,et al.Dynamic analysis and load-sharing characteristic of multiple pinion drives in tunnel boring machine[J].Journal of Mechanical Science and Technology,2013,27(5):1385-1392.
[5] YANG Yang,LI Ming,HU Minghui,et al.Influence of controllable parameters on load sharing behavior of torque coupling gear set[J].Mechanism and Machine Theory,2018,121:286-298.
[6] 巫世晶,任辉,朱恩涌,等.行星齿轮传动系统动力学研究进展[J].武汉大学学报:工学版,2010,43(3):398-403.
WU Shijing,REN Hui,ZHU Enyong,et al.Research advances for dynamics of planetary gear trains[J].Engineering Journal of Wuhan University,2010,43(3):398-403.
[7] KAHRAMAN A.Natural modes of planetary gear trains[J].Journal of Sound and Vibration,1994,173(1):125-130.
[8] 张俊,宋轶民,张策,等.2K-H型直齿行星传动自由振动分析[J].天津大学学报,2010,43(1):90-94.
ZHANG Jun,SONG Yimin,ZHANG Ce,et al.Analysis of free vibration of 2K-H spur planetary gear set[J].Journal of Tianjin University,2010,43(1):90-94.
[9] 杨通强,宋轶民,张策,等.斜齿行星齿轮系统自由振动特性分析[J].机械工程学报,2005,41(7):50-55.
YANG Tongqiang,SONG Yimin,ZHANG Ce,et al.Property analysis of free vibration of helical planetary gear trans[J].Chinese Journal of Mechanical Engineering,2005,41(7):50-55.
[10] 张俊,刘先增,焦阳,等.基于刚柔耦合模型的行星传动固有特性分析[J].机械工程学报,2014,50(15):104-112.
ZHANG Jun,LIU Xianzeng,JIAO Yang,et al.Vibration analysis of planetary gear trains based on a discrete-continuum dynamic model[J].Chinese Journal of Mechanical Engineering,2014,50(15):104-112.
[11] PARKER R G.A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J].Journal of Sound and Vibration,2000,236(4):561-573.
[12] 秦大同,肖正明,王建宏.基于啮合相位分析的盾构机减速器多级行星齿轮传动动力学特性[J].机械工程学报,2011,47(23):20-29.
QIN Datong,XIAO Zhengming,WANG Jianhong.Dynamic characteristics of multi-stage planetary gears of shield tunneling machine based on planet mesh phasing analysis[J].Chinese Journal of Mechanical Engineering,2011,47(23):20-29.
[13] 卜忠红,刘更,吴立言.滑动轴承支承人字齿轮行星传动固有特性分析[J].机械工程学报,2011,47(1):80-88.
BU Zhonghong,LIU Geng,WU Liyan.Natural characteristics analysis on herringbone planetary gear trains with slide bearing support[J].Chinese Journal of Mechanical Engineering,2011,47(1):80-88.
[14] BU Z,LIU G,WU L.Modal analyses of herringbone planetary gear train with journal bearings[J].Mechanism and Machine Theory,2012,54:99-115.
[15] REN Fei,QIN Datong,LIM Teik Chin,et al.Study on dynamic characteristics and load sharing of a herringbone planetary gear with manufacturing errors[J].International Journal of Precision Engineering and Manufacturing,2014,15(9):1925-1934.